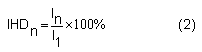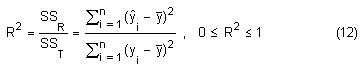Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Energética
versión On-line ISSN 1815-5901
Energética vol.35 no.3 La Habana sep.-dic. 2014
APLICACIONES INDUSTRIALES
Aplicación de modelos de regresión lineal para determinar las armónicas de tensión y corriente
Application of linear regression models to determine the current and voltage harmonics
MSc. Juan M. Astorga Gómez
Instituto Tecnológico, Universidad de Atacama, Copiapó, Chile.
RESUMEN
En este artículo se evalúan las armónicas individuales de tensión como función de las armónicas individuales de corriente usando los análisis estadísticos de regresión lineal simple, regresión polinomial y regresión lineal múltiple. Para la selección del modelo, se usan el coeficiente de determinación R2 y el criterio de información de Akaike (AIC). Se utiliza como caso de estudio un sistema eléctrico de un proceso minero ubicado en la región de Atacama Copiapó Chile, que ocupa la técnica de electro obtención de cobre como parte principal de su proceso productivo. Se muestran y comparan los resultados para los distintos modelos estadísticos y se discute la información de éstos para el estudio de calidad de energía. Finalmente, usando el modelo que mejor se ajusta a las mediciones de armónicas de tensión y corriente, se muestran algunas predicciones para la componente armónica dominante de tensión.
Palabras clave: armónicas, calidad de la energía, regresión lineal múltiple.
ABSTRACT
This paper assesses the individual voltage harmonics as a function of the individual current harmonics using the statistical analyses of simple linear regression, polynomial regression and multiple linear regression. For model choice, the coefficient of determination R2 and Akaike information criterion (AIC) are used. A mining process electrical system located in the Atacama Copiapó Chile, is used as a case study. This uses the technique copper electrowining as the main part of its production process. The results for different statistical models are shown and their information discussed for the power quality study. Finally, using the model that better fits to the measurements of voltage and current harmonics, some predictions for the dominant voltage harmonic are shown.
Key words: harmonics, power quality, multiple linear regression.
INTRODUCCION
Determinar la influencia de las armónicas de tensión y corriente en los sistemas eléctricos industriales es de gran importancia para la evaluación de la calidad de la energía y la administración eficiente del recurso energético [1-2]. Usualmente, para medir la influencia de los armónicos en los sistemas eléctricos se usan los índices de distorsión armónica total de tensión (THDV) y distorsión armónica total de corriente (THDI), que se obtienen a partir de los registros que almacenan los equipos analizadores de calidad de energía eléctrica. El cálculo de estos indicadores [3] se muestra en la ecuación (1).
En la ecuación (1), Vn es la magnitud de la tensión a la frecuencia de orden n, V1 es la magnitud de la tensión a la frecuencia fundamental, In es la magnitud de la corriente a la frecuencia de orden n y I1 es la magnitud de la corriente a la frecuencia fundamental (En Chile la frecuencia fundamental es 50 Hertz).
Por otro lado, la distorsión armónica individual IHD (individual harmonic distortion) mide el nivel de contenido armónico de la componente de orden n respecto del valor de referencia conocido como fundamental. El IHD se define como la razón entre el valor RMS de la componente armónica individual de orden n y el valor RMS de la componente fundamental [4]. La armónica que tenga la magnitud más alta de IHD será la armónica dominante del sistema. La ecuación (2), muestra el cálculo de la distorsión armónica individual.
Algunos autores [1-2], han desarrollado modelos estadísticos de regresión lineal para evaluar las componentes armónicas, considerando a la distorsión armónica total (THD) de tensión y/o corriente como variable de interés, esto debido a que en sus estudios se analizan cargas de distinta naturaleza (residencial, comercial e industrial) en un mismo registro de datos, y entonces, el THD resulta ser un buen indicador para esa condición, otros autores [5], proponen modelos de series de tiempo para la estimación de las armónicas. En este artículo en cambio, se estudian los modelos de regresión lineal simple, regresión polinomial de orden 2, regresión polinomial de orden 3 y regresión lineal múltiple, tomando como variable de respuesta a la distorsión armónica individual de tensión y como variable predictora a la distorsión armónica individual de corriente. Dado que el sistema de estudio corresponde a una carga de tipo industrial exclusiva, la distorsión armónica individual (IHD) resulta ser un buen indicador. La carga tiene como elemento principal un convertidor de potencia de corriente alterna a corriente continua con gran cantidad de elementos semiconductores, y por tanto, el monitoreo y control de los niveles de contaminación armónica son de gran interés para el usuario. Los criterios que se usan en este artículo para evaluar los niveles permisibles de distorsión armónica se han extraído desde las norma IEEE Std. 519-1992 [6] y de la norma chilena Norma Técnica de Seguridad y Calidad de Servicio [7].
El artículo se estructura de la siguiente manera. En la primera parte se presentan las principales características de los modelos de regresión que son tratados en este trabajo y se describen los indicadores que se utilizan para validar y seleccionar los modelos propuestos. Luego, se muestran los resultados del procesamiento de datos de las mediciones en la carga minera, se aplican los distintos modelos de regresión, se comparan los resultados de cada modelo, se evalúa su eficiencia y se selecciona el mejor modelo. Posteriormente, se desarrollan algunas predicciones para la distorsión armónica individual de tensión usando el modelo que haya tenido el mejor ajuste. Finalmente, se entregan las principales conclusiones de la investigación.
METODOLOGIA
Modelo de regresión lineal simple
Los modelos de regresión lineal son ampliamente usados en la ingeniería ya que sirven para analizar el comportamiento de las variables de entrada (o regresora) y salida (o respuesta) estableciendo predicciones y estimaciones [8]. En este trabajo la variable regresora corresponde a la distorsión armónica individual de corriente y la variable de respuesta corresponde a la distorsión armónica individual de tensión.
La ecuación (3), muestra la representación de un modelo de regresión lineal simple, donde Ŷ es la respuesta, X es la variable regresora, β0 y β1 son los parámetros del modelo o coeficientes de regresión y ε es el error del modelo.
La ecuación (4), muestra el modelo ajustado de regresión lineal simple, donde Ŷ es el valor estimado o esperado de la variable de respuesta para la variable regresora X. Los estimadores de los parámetros del modelo son calculados por el método de los mínimos cuadrados usando las ecuaciones (5) y (6).
Modelo de regresión polinomial
Los modelos de regresión polinomial se usan cuando la variable de respuesta muestra un comportamiento curvilíneo o no lineal [8]. La ecuación (7), describe el modelo de regresión polinomial de orden k en una variable regresora y la ecuación (8), muestra el modelo ajustado de regresión polinomial de orden k. Los estimadores de los parámetros del modelo se obtienen por el método de los mínimos cuadrados usando la ecuación (9), donde y, X, X' son vectores. En este trabajo se aplican los modelos de regresión polinomial de orden 2 y orden 3 en una variable regresora.
Modelo de regresión lineal múltiple
La ecuación (10), describe un modelo de regresión lineal múltiple y la ecuación (11), muestra el modelo ajustado de regresión lineal múltiple. En este modelo la variable de respuesta se puede relacionar con k variables regresoras. Se justifica aplicar el modelo de regresión lineal múltiple cuando interviene más de una variable regresora [8]. Los estimadores de los coeficientes de este modelo se obtienen a partir de la ecuación (9). En este trabajo se consideraron 3 variables regresoras.
En los modelos de regresión lineal múltiple se debe evaluar la presencia de la multicolinealidad, que aparece cuando existe una dependencia casi lineal entre las variables regresoras del modelo [8]. La multicolinealidad provoca problemas en la determinación de los estimadores de los coeficientes del modelo. La técnica más común que se usa para detectar la presencia de multicolinealidad es el análisis de la matriz de correlación.
Coeficiente de determinación R2
El coeficiente de determinación R2 mide la proporción de la variación de la respuesta Y que es explicada por el modelo de regresión [8]. El coeficiente R2 se calcula usando la ecuación (12), donde SSR es la medida de variabilidad del modelo de regresión y SST corresponde a la medida de variabilidad de Y sin considerar el efecto de la variable regresora X.
Si el valor de R2 se acerca a 1, entonces se tiene un buen ajuste y el modelo de regresión es capaz de explicar adecuadamente la variación de la variable de respuesta Y.
Criterio de información de Akaike (AIC)
El criterio de información de Akaike (AIC) es un indicador que permite seleccionar un modelo estadístico basándose en la teoría de información y en las propiedades del método de máxima verosimilitud [9]. Para calcular el AIC se utiliza la ecuación (13), donde k es el número de parámetros del vector de parámetros θ del modelo y ML es la función de máxima verosimilitud.
Cuando se comparan dos o más modelos estadísticos, se selecciona el que tiene el menor AIC [9].
Selección de las variables regresoras y de respuesta para cada modelo
Los modelos de regresión que se discuten en este trabajo tienen como variable de respuesta a la distorsión armónica individual dominante de tensión, mientras que las variables regresoras corresponden a la distorsión armónica individual de corriente de igual y/o menor orden que la armónica dominante de tensión (según el modelo). En la tabla 1, se muestran las variables que fueron consideradas para cada modelo.
Descripción del proceso minero
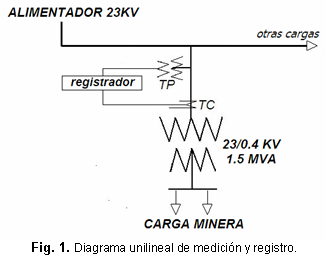
La figura 1, muestra el diagrama unilineal de medición y registro en la carga minera. Esta carga se encuentra ubicada en las cercanías de la ciudad de Copiapó, región de Atacama Chile y corresponde a un proceso minero cuyo principal equipo eléctrico es un convertidor de potencia de corriente alterna a corriente continua. Se almacenaron los registros de la distorsión armónica individual de tensión y corriente durante 7 días consecutivos, con tiempos de muestreo de 10 minutos.
El nivel de cortocircuito máximo en la barra de 23 KV es 1072,7 A y la corriente máxima de plena carga en 23 KV es 37,65 A, por lo tanto, la relación corriente máxima de cortocircuito sobre corriente máxima de carga en el punto común de conexión PCC) es 28,5.
RESULTADOS
Al analizar los registros de distorsión armónica se detectó que la armónica dominante de tensión es la de orden 7, con una magnitud media de 2,17 %. Las armónicas de corriente de orden 3, 5 y 7, registraron las magnitudes medias de 3,10 %, 2,12 % y 10,29 %, respectivamente. En la figura 2, se muestra el perfil de la distorsión armónica de tensión de orden 7 y los perfiles de distorsión armónica de corriente de orden 3, 5 y 7, durante los 7 días de registro.
Como la relación corriente máxima de cortocircuito sobre corriente máxima de plena carga es 28,5, el nivel máximo de distorsión armónica individual de corriente para armónicas de orden inferior a 11 no debe superar el 7 % [6-7]. Por otro lado, para tensiones inferiores a 69 KV la distorsión armónica individual de tensión no debe superar el 3 % [6], mientras que para sistemas con tensiones menores o iguales que 110 KV, la distorsión armónica de orden 7 debe ser menor a 5 % [7]. Considerando lo descrito en el párrafo anterior, la distorsión armónica individual de corriente de orden 7 no cumple con lo establecido por la norma IEEE 519-1992 [6], ni por la norma chilena [7], mientras que las distorsión armónica individual de corriente de orden 5 y orden 3 cumplen con lo exigido por estas normas. La magnitud de la distorsión armónica individual de corriente es menor que 3 % y 5 %, por lo tanto, cumple con lo exigido por las normas [6-7].
Aplicación de los modelos de regresión
Para aplicar los modelos de regresión al ajuste de los datos de las mediciones de campo en la carga minera, se utilizó el software de distribución libre R [10]. Utilizando el paquete Rcmdr se obtuvieron las gráficas de dispersión de las variables de respuesta y regresoras y los resultados analíticos de los modelos. La figura 3, muestra el comportamiento gráfico de los modelos de regresión lineal simple, polinomial de orden 2 y polinomial de orden 3, mientras que la tabla 2, describe el desempeño de cada modelo de regresión.
En el análisis del modelo de regresión lineal múltiple no se observó presencia de multicolinealidad entre las variables regresoras, ya que ningún término fuera de la diagonal de la matriz de correlación supera la magnitud 0,7 [11], por lo tanto, es recomendable considerar en el modelo de regresión múltiple las tres variables regresoras. La tabla 3, muestra los coeficientes de la matriz de correlación para las variables regresoras del modelo de regresión lineal múltiple.
Selección del modelo de regresión
Dado los resultados de la tabla 2, el valor más alto de R2 y el valor más bajo del AIC (criterio de información de Akaike) se logra con el modelo de regresión lineal múltiple, por lo tanto, este modelo es el que se selecciona como el más adecuado para el ajuste de los datos de distorsión armónica individual de tensión y corriente. La ecuación (14), muestra el modelo seleccionado.
Usando el software R [10], se obtienen los intervalos de confianza para cada parámetro del modelo de regresión lineal múltiple, estos resultados se muestran en la tabla 4.
Pronósticos usando el modelo de regresión ineal múltiple
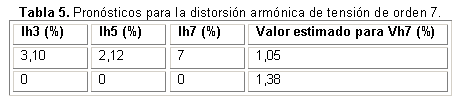
Usando el modelo de la ecuación (14), se realizan dos pronósticos. En el primer pronóstico se estima el valor que tomaría la distorsión armónica individual de tensión de orden 7 cuando la distorsión armónica de corriente de orden 7 se reduce al 7 % (sin modificar los valores medios de las distorsiones armónicas de corriente de orden 3 y 5) y cuando los tres valores de distorsión armónica de corriente se reducen a 0 %. En el segundo pronóstico se estima el valor de la distorsión armónica de corriente de orden 7 que hace que la distorsión armónica individual de tensión aumente a 3 % y a 5 % (cuando no se modifican los valores medios de las distorsiones armónicas de corriente de orden 3 y 5). Estos resultados se muestran en las tablas 5 y 6.
De los pronósticos de las tablas 5 y 6, se puede apreciar que si se reduce la contaminación armónica de corriente de orden 3, 5 y 7 a 0 % (instalando filtros de armónicos), la distorsión armónica de tensión de orden 7 se reduce a 1,38%. Por otro lado, si la componente armónica dominante de corriente de orden 7 aumenta sobre 12,73 %, la distorsión armónica de tensión de orden 7 aumenta sobre 3 %, no cumpliendo con lo indicado en la norma IEEE 519-1992. Por otro lado, si la componente armónica dominante de corriente de orden 7 aumenta sobre 18,6 %, entonces la distorsión armónica de tensión de orden 7 aumenta sobre 5 %, no cumpliendo con lo establecido en la norma técnica chilena de calidad y seguridad de servicio.
Restricciones del modelo de regresión ineal múltiple
Para valores de distorsión armónica de corriente de orden 7 menores que 4 % (manteniendo constantes los valores medios de la distorsión armónica de corriente de orden 3 y 5) la distorsión armónica de tensión de orden 7 se hace negativa, perdiendo interpretación física. Para valores de distorsión armónica de corriente de orden 3 mayores que 6 % (manteniendo constantes los valores medios de la distorsión armónica de corriente de orden 5 y 7) la distorsión armónica de tensión de orden 7 se hace negativa, perdiendo interpretación física.
CONCLUSIONES
En este trabajo, se probaron los modelos de regresión lineal simple, regresión polinomial de orden 2, regresión polinomial de orden 3 y regresión lineal múltiple para describir la relación entre la distorsión armónica individual de tensión y la distorsión armónica individual de corriente en un proceso minero, siendo el modelo de regresión lineal múltiple el que mejor ajustó los datos de las mediciones del proceso, con mejor coeficiente de determinación R2 (0,8124) y menor criterio de información de Akaike (459,25).
Los pronósticos realizados con el modelo de regresión lineal múltiple, permiten estimar la distorsión armónica individual de tensión y corriente del sistema eléctrico y direccionar medidas correctivas para el control del contenido armónico del proceso. Cuando se analizan las armónicas de un sistema eléctrico con carga homogénea, el modelo de regresión lineal múltiple describe adecuadamente la distorsión armónica individual de tensión como función de la distorsión armónica individual de corriente.
REFERENCIAS
1. WU, C.J.; et al., "Application of regression models to predict harmonic voltage and current growth trend from measurement data at secondary substations". IEEE Transactions on Power Delivery, 1998, vol.13, n.3, p. 793-799, [Consultado: junio 2013], Disponible en: http://ieeexplore.ieee.org/iel4/61/15033/00686976.pdf, ISSN 0885-8977.
2. VLAHINI?, S.; et al., "Measurement and analysis of harmonic distortion in power distribution systems". Electric Power Systems Research, 2009, vol.79, n.7, p. 1121-1126, [Consultado: marzo de 2013], Disponible en: http://www.sciencedirect.com/science/article/pii/S0378779609000558, ISSN 0378-7796.
3. ARRILLAGA, J.; WATSON, N.R., "Power system harmonics". England: John Wiley & Sons, 2003, 389 p., ISBN: 0-470-85129-5.
4. SANKARAN, C., "Power quality". Florida: CRC Press, 2001, 216 p., ISBN: 0-8493-1040-7.
5. JAIN, S.K.; SINGH, S.N., "Harmonics estimation in emerging power system: Key issues and challenges". Electric Power Systems Research, 2011, vol.81, n.9, p. 1754-1766, [Consultado: abril de 2013], Disponible en: http://www.sciencedirect.com/science/article/pii/S0378779611001088, ISSN 0378-7796.
6. IEEE, "IEEE Recommended practices and requirements for harmonic control in electrical power systems". IEEE Std. 519-1992, New York: IEEE, 1992, ISBN: 1-55937-239-7.
7. Gobierno de Chile, Comisión Nacional de Energía C.N.E., "Norma técnica de seguridad y calidad de servicio". Santiago de Chile, Octubre de 2009, [Consultado: mayo 2013], Disponible en: http://www.cne.cl/normativas/energias/electricidad/528-norma-tecnica.
8. MONTGOMERY, D.; et al., "Introducción al análisis de regresión lineal". México: Ed. Limusa Wiley, 2006, 588 p., ISBN: 970-24-0327-8.
9. AKAIKE, H., "A new look at the statistical model identification". IEEE Transactions on Automatic Control, 1974, vol.19, n.6, p. 716-723, [Consultado: marzo 2013], Disponible en: http://ieeexplore.ieee.org/iel5/9/24140/01100705.pdf, ISSN 0018-9286.
10. R Development Core Team, "The R Project for Statistical Computing". [Programa de computación], [Consultado: abril 2013], Disponible en: http://www.r-project.org.
11. DE LA GARZA, J.; et al., "Análisis estadístico multivariante, un enfoque teórico y práctico". México: Ed. Mc Graw-Hill, 2013, 712 p., ISBN: 978-607-15-0817-1.
Recibido: noviembre de 2013
Aprobado: marzo de 2014
Juan Miguel Astorga Gómez, Ingeniero Eléctrico, Magister (c) en Ciencias con mención en Estadística Industrial, Profesor Asistente, Instituto Tecnológico, Universidad de Atacama, Copiapó, Chile. e-mail: juan.astorga@uda.cl