ARTÍCULO ORIGINAL

 

Simulación de un sistema tribológico formado por sustrato recubrimiento rugoso usando métodos numéricos

 

Simulation tribological system formed by substrate roughness coating using numeric methods

 

 

Eduardo A. Pérez-Ruiz^I, German E. Muñoz-Tovar^I, Roberto M. Souza^II, Luis-Ivan Negrín-Hernández^III

^I Universidad de Ibagué, Colombia.
^II Universidad de Sao Paulo, Sao Paulo, Brasil.
^III Universidad Central Marta Abreu de las Villas, Facultad de Ingeniería Mecánica. Santa Clara, Cuba

 

 

---

RESUMEN

Esta investigación se centra en simular y analizar usando el Método de los Elementos Finitos, los esfuerzos obtenidos en un sistema sustrato+recubrimiento como consecuencia del contacto con una partícula rígida, sometida a carga normal y deslizamiento a lo largo de la superficie del sistema, la cual cuenta con una rugosidad Ra de 0,36?m. Los resultados evidencian la importancia de considerar la rugosidad del sistema recubierto durante la simulación del ensayo de rayado, contrario a las simulaciones que reporta la literatura, ya que esta afecta el comportamiento de esfuerzos y deformaciones durante el contacto y deslizamiento. Además los resultados sugieren que al considerar la rugosidad del sistema, aumenta la posibilidad de surgimiento prematuro de grietas durante el ensayo de rayado.

Palabras claves: método de los elementos finitos, sistemas recubiertos, rugosidad, esfuerzos.

---

ABSTRACT

This research focuses on simulate and to analyze using Finite Element Method, the stresses behavior obtained in a system (substrate+coating) as a result of the contact with a rigid particle under normal load and sliding along the surface of the system, which has roughness Ra of 0,36?m. The results show that in the scratch test simulation, the roughness of coated system must be considered contrary to the literature simulations of this field, since this affects the stresses and deformations behavior during contact and sliding. Thus, to increase surface roughness peaks greater possibility of inducing stress cracking.

Key words: finite element method, coated systems, roughness, stresses.

---

 

INTRODUCCIÓN

El estudio entre dos superficies que se encuentran en contacto y movimiento relativo (tribología), es un asunto de análisis y discusión, especialmente cuando son utilizadas capas resistentes al desgaste en la superficie de los materiales [1]. Gracias al avance y uso de técnicas para deposición de materiales resistentes al desgaste (PVD, CVD) ha sido posible el diseño de sistemas recubiertos con el fin de buscar el mejoramiento tribológico (desgaste, lubricación, etc.) de componentes mecánicos [1-3].

Para la evaluación del comportamiento mecánico (esfuerzos y deformaciones) obtenidos en los sistemas recubiertos, según las características y parámetros utilizados en los procesos de deposición de materiales en capas superficiales, son comúnmente utilizados los ensayos de indentación [3-5], así como de rayado [6]. Durante este último ensayo son desarrollados campos de esfuerzos y deformaciones, los cuales son la causa de falla, bien sea adhesiva (levantamiento de la capa respecto sustrato) o cohesiva (grietas superficiales) de estos sistemas a lo largo del surco generado.

Para el estudio de los esfuerzos y las deformaciones a lo largo del surco generado en materiales metálicos, es bastante utilizado el método de los elementos finitos, el cual ha permitido el desarrollo de modelos 2D y 3D de sistemas recubiertos idealmente lisos [7-9].

De la misma forma, Li [7] revela que el modelo realizado en 3D permite demostrar la gran acumulación dada por el material en contacto con la partícula deslizante, en la medida que esta se aleja del punto inicial de contacto. Igualmente permite la identificación de tres modos de contacto (estático, deslizamiento y arado) durante el deslizamiento sobre el sistema recubierto, lo que trae como consecuencia la aparición de esfuerzos compresivos en el material acumulado y esfuerzos de tracción en el surco creado después del paso de la partícula. El pandeo o curvatura de la capa (recubrimiento) son producidos por la acumulación de los esfuerzos de compresión generados en la punta de la partícula, así como los esfuerzos de tracción son los responsables de la iniciación de grietas transversales, lo que puede ser utilizado para el estudio de la tenacidad de la capa.

Para M. Tkaya et al [9], se evidencia un mecanismo de correlación entre el desgaste y el coeficiente de fricción, en donde el aumento de este, así como el del ángulo de ataque de la partícula rígida, provocan una transición entre la acumulación de material en los costados del surco (arado) y el corte que lleva a la remoción del material.

Por otra parte, investigadores [9, 10] han comprobado que el incremento en el surco generado durante el deslizamiento de una partícula rígida, está directamente relacionado con el aumento en la carga normal aplicada y con la fricción generada, lo que trae como consecuencia altos valores de esfuerzos de tracción en la superficie por la acumulación de material (pile-up) en la parte delantera y lateral del contacto con la partícula que desliza, así como la presencia de esfuerzos compresivos en la misma región, específicamente debajo de la capa (interface sustrato recubrimiento). De la misma forma, se ha evidenciado que el espesor y el módulo elástico de la capa utilizada como recubrimiento son los principales parámetros que afectan la magnitud de los esfuerzos en el sistema recubierto, en donde el espesor afecta directamente la rigidez y el módulo elástico del material de la capa favorece el flujo plástico del sustrato en el sistema.

Como ha sido demostrado en la literatura, los análisis del comportamiento mecánico de los sistemas recubiertos han sido modelados y simulados considerando superficies idealmente lisas, por esta razón, el objetivo fundamental de este estudio está dirigido específicamente a analizar el comportamiento mecánico (esfuerzo y deformación) de un sistema recubierto en donde se considera la rugosidad presente en la capa del sistema recubierto durante el contacto y deslizamiento de una partícula rígida sobre el mismo.

 

MÉTODOS Y MATERIALES

El modelo computacional para el análisis y simulación de esfuerzos y deformaciones generados después del contacto y deslizamiento de una partícula rígida sobre un sistema recubierto rugoso, fue realizado utilizando el software para análisis ABAQUS.

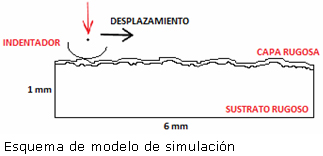
El esquema de la geometría del sistema que se presenta es el siguiente:

Debido a que en un ensayo de rayado el desplazamiento puede llegar a ser de 10 mm y teniendo en cuenta que el espesor de la muestra debe ser por lo menos 8 o 10 veces la profundidad de la huella y que la distancia inicial de contacto desde el borde de la muestra no debe ser menor de 3 o 4 veces el diámetro de la huella [7, 9], se considera un modelo 2D, compuesto por un sustrato rugoso con dimensiones de 6mm de largo por 1 mm de espesor (6x1 mm). De la misma forma se considera un indentador esférico (partícula de deslizamiento), aunque el tamaño del indentador utilizado en ensayos de rayado es de 0,20 mm de radio (característico Rockwell C) como objeto de estudio se considera un indentador de 0,25 mm de radio.

Con el fin de conseguir proporcionalidad con las dimensiones del modelo y tomando como referencia algunos autores [7, 9, 10], el indentador desliza sobre el sustrato una distancia horizontal de 2,5 mm.

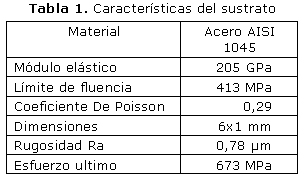
Para el sustrato se utilizó el acero AISI 1045. Las propiedades elásticas (E= 205GPa y v=0,29) y plásticas del sustrato fueron obtenidas de datos de ensayos experimentales de tracción presentes en [12].

El acabado superficial considerado en el sustrato alcanza un valor de rugosidad media Ra= 0,78 µm, el cual es el acabado característico para los ensayos de desgaste ASTM G-99 y fue obtenido de forma experimental utilizando un rugosímetro Mitutoyo SJ201. En la tabla 1 se presentan las características de sustrato.

Características del recubrimiento

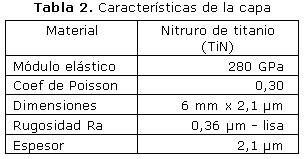
Para el recubrimiento se utilizó una capa de Nitruro de Titanio (TiN) con comportamiento elástico cuyas propiedades aparecen en la tabla 2 [10].

Para el adecuado modelamiento, simulación y análisis del efecto de la rugosidad del sistema recubierto, es considerada una primera simulación con un valor de rugosidad media Ra= 0,36 µm, la cual se aproxima a mediciones encontradas en la literatura para capas de TiN. En una segunda simulación la superficie de la capa es considerada idealmente lisa. Para los dos casos es considerado un espesor de capa de TiN de 2,1 µm. En la tabla 2 se presentan las características del recubrimiento.

La partícula que se considera como indentador presenta un radio de 0,25 mm y es modelada como cuerpo rígido y sobre ella es aplicada la carga normal y el desplazamiento durante la simulación

El modelo estudiado considera una carga normal de 15 N aplicada sobre el indentador, la cual se incrementa durante el desplazamiento, iniciando en 0 hasta obtener el valor máximo (15 N). La magnitud de la carga es asumida teniendo en cuenta que está dentro del rango de cargas utilizadas en un ensayo de rayado, las cuales pueden llegan hasta los 200 N.

Se debe tener en cuenta que en el modelo, el sustrato tiene restricciones de movimiento en todas las direcciones, esto se realiza con el fin de garantizar que el sistema recubierto no presente movimiento relativo durante la aplicación de la carga. Así mismo, el indentador únicamente puede desplazarse de forma horizontal y vertical.

En la malla desarrollada durante el estudio se consideran elementos triangulares y cuadriláteros, siendo preferidos estos últimos por su isotropía geométrica. Teniendo en cuenta que el modelo presenta irregularidades en la parte superior (rugosidad) los cuadriláteros pierden su forma original, por ese motivo se utilizan en esta zona elementos triangulares.

 

RESULTADOS Y DISCUSIÓN

Sistema recubierto con capa rugosa

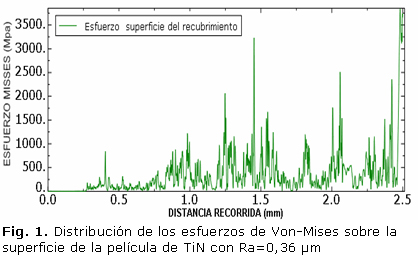
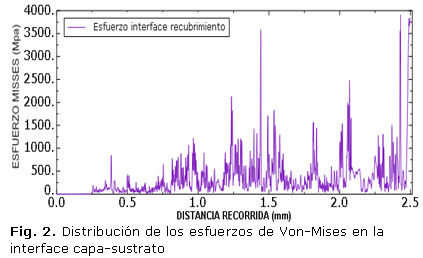
Las figuras 1 y 2 presentan los resultados de la distribución de esfuerzos equivalentes (Von Mises), a lo largo de la superficie de la película delgada de TiN con rugosidad media de 0,36 µm y en la interface capa/sustrato respectivamente, calculados en función de la distancia recorrida (mm) y siendo medidos desde el inicio del desplazamiento hasta el final del recorrido de la partícula rígida (2,5 mm).

Es posible observar que el comportamiento entre las dos gráficas es similar, conservando practicamente los mismos valores de esfuerzo (rango de 250-1000 MPa), a lo largo de la distancia recorrida. Es importante identificar que en algunos puntos cercanos a los 1,5 y 2 mm recorridos, tanto en la superficie como en la interface del sistema recubierto, se presentan picos con altos valores de esfuerzo, lo cual puede ser causado debido a la diferencia entre la rugosidad del sustrato y la de la capa (0,78 µm - 0,36 µm), lo cual ocasiona que en algunos puntos la capa no conserve el espesor de 2,1 µm. Lo anterior puede traer como consecuencia una posible aparición de fallas (grietas) en estos puntos. Ejemplo de este fenómeno se puede observar a la distancia de 1,47 mm como muestra la figura 3 y según Holmberg et al [10] un recubrimiento de alto espesor presenta mayor capacidad de carga.

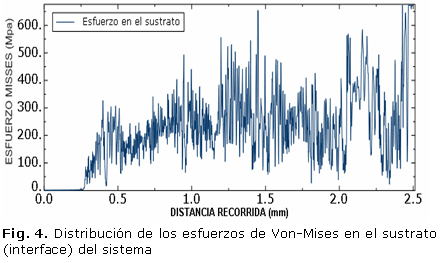
En la figura 4 se presenta el comportamiento de los esfuerzos equivalentes (Von Mises) sobre el sustrato en la interface del sistema recubierto Es posible observar que el esfuerzo se concentra en un rango de valores entre 100 y 400 MPa aproximadamente, sin embargo en la distancia de 1,47 mm, al igual que en los esfuerzos en la superficie y en la interface se observa un pico con valor aproximado de 673 MPa, el cual es el valor de la resistencia máxima o última para el acero AISI 1045. Lo anterior indica que en ese punto, tal vez, por la reducción en el espesor de la capa protectora el sustrato alcanza valores de esfuerzo próximos a la condición de falla.

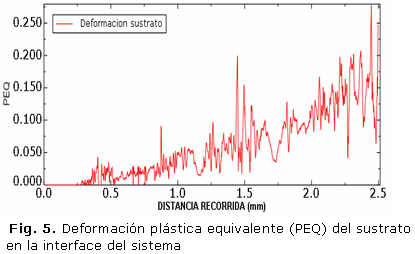
La figura 5 muestra la deformación plástica equivalente (PEQ) del sustrato en la interface. Como es de esperar, se observa un comportamiento creciente de la deformación plástica equivalente; es decir a medida que aumenta la distancia recorrida aumenta la deformación. Así mismo se observa un pico en el valor de la deformación a 1,47 mm, siendo correspondiente con el pico obtenido en el gráfico de esfuerzo.

Sistema recubierto con capa idealmente lisa

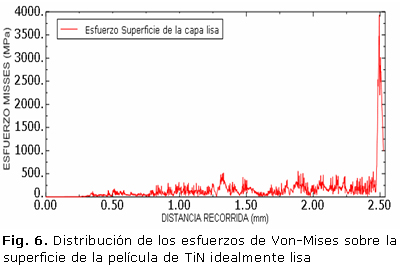
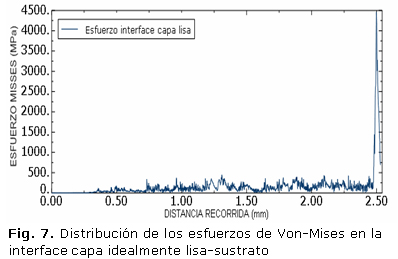
Las figuras 6 y 7 presentan los resultados de la distribución de esfuerzos equivalentes (Von Mises), a lo largo de la superficie de la película delgada de TiN, considerada idealmente lisa y en la interface capa/sustrato respectivamente, calculados en función de la distancia recorrida (mm). Es posible observar que el comportamiento de los esfuerzos es similar y no presentan puntos específicos en los cuales se generan picos, así mismo se puede observar que los valores obtenidos en los dos casos (superficie e interface) no sobrepasan el valor de 500 MPa.

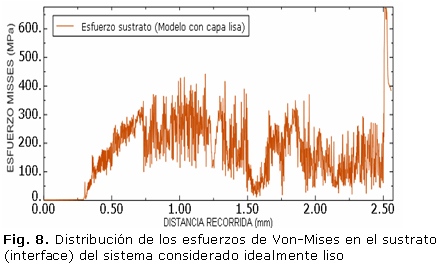
En la figura 8 se presenta el comportamiento de los esfuerzos equivalentes (Von Mises) sobre el sustrato en la interface del sistema recubierto a lo largo de la distancia de deslizamiento. Se observa que al compararla con la figura 4, los valores de esfuerzo a lo largo de la distancia deslizada no superan el valor de 400 MPa.

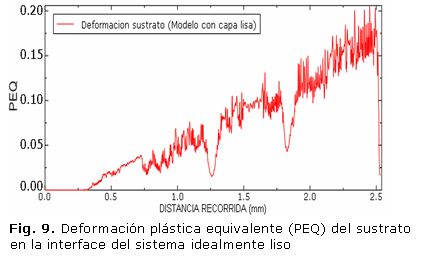
La figura 9 presenta el comportamiento de la deformación plástica equivalente (PEQ) del sustrato en la interface, para el sistema recubierto idealmente liso, calculada en función de la distancia recorrida.

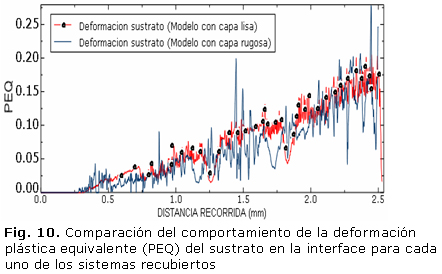
En la figura 10, es presentado el comportamiento que se genera en cuanto a la deformación plástica equivalente, en el sustrato en la interface en un sistema recubierto con rugosidad de capa de 0,36 µm y un sistema recubierto con capa idealmente lisa.

La figura anterior, permite identificar que para el sistema con capa rugosa se presenta un pico de deformación en el punto 1,47 mm de la distancia de deslizamiento, mientras que para el sistema con capa idealmente lisa no se evidencia un pico sobresaliente. Así mismo se evidencia que en los dos casos el comportamiento de la deformación plástica es ascendente según avanza la distancia de deslizamiento, lo que es de esperar ya que el indentador (partícula rígida) debe ir acumulando material en la medida que avanza.

 

CONCLUSIONES

Los resultados obtenidos a través de un modelo de simulación 2D, evidencian que al aumentar la carga de contacto, de forma proporcional con la distancia de deslizamiento, de una partícula rígida sobre un sistema recubierto, son incrementados los valores de esfuerzo equivalente (Mises) y la deformación plástica, tanto en la superficie del sistema como en la interface del conjunto.

Según los resultados de simulación, es ratificada la importancia del uso de capas protectoras de materiales resistentes al desgaste por su capacidad de resistencia, ya que como se evidenció, para este caso, los esfuerzos presentes en la superficie de la capa protectora pueden presentarse en el intervalo de 250-1000 MPa, mientras que el valor de los esfuerzos en la superficie del sustrato (altamente dúctil) se presentan en el intervalo de 100 a 400 MPa.

La rugosidad inherente a los procesos de fabricación de las piezas es un parámetro de alta incidencia en el comportamiento a la falla de las mismas. El uso de acabados superficiales finos (valores de rugosidad media y bajos) son favorables en el comportamiento de los esfuerzos. Como se presentó para este estudio en particular, la superficie con rugosidad media de 0,36 µm alcanzó altos valores de esfuerzo generados durante el contacto (250-1000 MPa), mientras que el uso de la capa con superficie idealmente lisa generó esfuerzos del orden de 100-400 MPa.

 

REFERENCIAS

1. Holmberg, K., Matthews A. y Ronkaine, H. "Coatings tribology contact mechanisms and surface design". Tribology International, 1998, vol. 31, p. 107-120. ISSN 0301-679X

2. Hogmark, S., Jacobson, S. y Larsson, M. "Design and evaluation of tribological coatings". Wear, 2000, vol 246, p. 20-33. ISSN: 0043-1648

3. Agudelo, L. C., Restrepo, E. y De La Roche, J. "Simulación de propiedades mecánicas de películas delgadas de carburo de tungsteno a partir del Modelo Monte Carlo". Revista Tecno Lógicas. 2012, nº. 29, p. 105-117. ISSN 0123-7799.

4. Sharma, K., Bhasin, V., Vaze, K. et al. "Numerical simulation with finite element and artificial neural network of ball indentation for mechanical property estimation". Sadhana. 2011. vol. 36, p. 181-192. ISSN 0973-7677.

5. Isaza, J., Mariaka, I. y Ramirez, J. "Caracterización de propiedades mecánicas mediante análisis inverso del Método de los Elementos Finitos combinado con ensayo de indentación". Dyna. 2013. vol. 80, nº.179, ISSN 0012-7353.

6. Schwarzer, N., Duong, Q. H., Bierwisch, N. et al. "Optimization of the Scratch Test for specific coating designs". Surface & Coatings Technology, 2011, vol. 206 p. 1327-1335. ISSN 0257-8972

7. Li, J. y Beres, W. "Three-dimensional finite element modelling of the scratch test for a TiN coated titanium alloy substrate". Wear, 2006, vol. 260, p. 1232-1242. ISSN 0043-1648

8. Torres, J. P., Sanchez, L., Pardo, E. et al. "Determinación de los parámetros constitutivos del polimetilmetacrilato (PMMA) mediante análisis inverso y simulación por elementos finitos". Mecánica Computacional. 2011. vol. XXX, p. 827-835 ISSN 1666-6070.

9. Tkaya, M., Zahouani, H. y Mezlini, S. "The effect of damage in the numerical simulation of a scratch test". Wear. 2007, vol. 263, p. 1533-1539. ISSN 0043-1648

10. Holmberg, K., Laukkanen, A., Ronkainen, H. et al. "Tribological contact analysis of a rigid ball sliding on a hard coated surface Part I: Modelling stresses and strains". Surface & Coatings Technology. 2006, vol. 200, p. 3793-3809. ISSN 0257-8972

11. Roa, J. J., Morales, M., Martínez, M. et al. "Curva tensión-deformación mediante indentación esférica para materiales cerámicos superconductores de YBCO-TSMG". Anales de Mecánica de la Fractura. 2009. vol. 2, p. 495-500, ISSN 0213-3725.

12. Meneses, A. Modelación del comportamiento de capas duras bajo cargas de indentación. Tesis de Doctorado. Instituto Politécnico Nacional. México. 2011. [Consultado el: 6 de febrero 2013]. Disponible en: http://www.repositoriodigital.ipn.mx/handle/123456789/8326

 

 

Recibido: 2 de julio de 2013.
Aceptado: 4 de octubre de 2013.

 

 

Eduardo A. Pérez-Ruiz. Universidad de Ibagué, Colombia.
Correo electrónico: [e-mail]