ARTÍCULO ORIGINAL
Determinación experimental del coeficiente de fricción dinámico suelo-metal en un suelo Ferralítico rojo
Experimental determination of the soil-metal of the dynamic coefficient friction in a Ferrasol
M. Sc. Ernesto Ramos Carbajal, Ing. Alexander Laffita, Dr. C. Armando García de la Figal, Dr. C. Pedro A. Valdés Hernández, Ing. Raúl Torres Cepero
Universidad Agraria de La Habana, Facultad de Ciencias Técnicas, Centro de Mecanización Agropecuaria, San José de las Lajas, Mayabeque, Cuba.
RESUMEN
Con el objetivo de conocer el valor del coeficiente fricción dinámico suelo-metal como dato de entrada para la evaluación de los modelos físicos matemáticos desarrollados con vista al diseño de parámetros geométricos de sondas utilizadas en la agricultura de precisión, se determinó experimentalmente sus valores para un suelo Ferralítico rojo en función de tres variables controladas: humedad volumétrica entre 20,5 y 26,1%; la velocidad de deslizamiento de la plancha metálica sobre el suelo, entre 0,673 y 1,234 m/s y para presiones específicas de 2,068 y 3,951 kPa. El intervalo de los valores del coeficiente de fricción dinámico obtenido, como primera aproximación, es de 0,57 a 0,82, en función de las variables independientes estudiadas. Éste manifiesta una tendencia de aumentar a medida que: disminuye la presión específica sobre el suelo; aumenta la velocidad inicialmente desde 0,59 hasta 0,9 m/s y, posteriormente, tiende a mantenerse constante hasta valores de 1,73 m/s, para un nivel de presión bajo (2,068 kPa) y a disminuir para un nivel de presión mayor (3,951 kPa). Las variables que más influyen en la variación del valor del coeficiente de fricción dinámico suelo-metal son, en orden descendiente: la presión, la velocidad y, por último, la humedad.
Palabras clave: fricción dinámica, suelo-metal, Ferralítico rojo.
ABSTRACT
With the objective of knowing the value of the coefficient friction dynamic soil-metal like entrance fact for the evaluation of the mathematical physical models developed with view to the design of geometric parameters of probes used in the agriculture of precision, it was determined their values experimentally for a soil red Ferrasol in function of three controlled variables: humidity volumetric between 20,5 and 26,1%; the speed of slip of the metallic iron on the soil, between 0,673 and 1,234 m/s and it stops specific pressures of 2,068 and 3,951 kPa. The interval of the values of the obtained dynamic coefficient of friction, as first approach, is from 0,57 to 0,82, in function of the studied independent variables. This apparent a tendency of increasing as: it diminishes the specific pressure on the soil; the speed increases initially from 0,59 up to 0,9 m/s and, later on, he/she spreads to stay constant until values of 1,73 m/s, for a low level of pressure (2,068 kPa) and to diminish for a level of more pressure (3,951 kPa). The variables that more influences in the variation of the value of the coefficient of friction dynamic soil-metal are, in descending order: the pressure, the speed and, lastly, the humidity.
Key words: dynamic friction, floor-metal, Red Ferrasol.
INTRODUCCIÓN
Los estudios relacionados con los suelos incluyen entre otros la mecánica de suelo y dentro de esta el estudio de la fricción que se considera una de las múltiples propiedades físico-mecánicas que presentan los mismos.
El estudio de la fricción ha tomado importancia en los últimos años, manifestándose en investigaciones en distintas áreas como la física, las ingenierías, ciencia de superficie y tribología, apareciendo en la literatura clásica de la Ingeniería Mecánica con son los textos de Beer ; Russell (1990) y Shigley (1990).
Sin embargo, el fenómeno de la fricción aún no ha sido comprendido del todo y todavía se encuentra en estudio, a pesar de lo investigado durante cientos de años por muchos de los científicos más brillantes como Leonardo da Vinci, Amontons, Coulomb, Reynolds y otros, (Bogart, 2004).
Durante el estudio de la fricción dinámica de la interacción suelo y otro material el coeficiente de fricción dinámico puede sufrir variación en ciertos rangos de velocidad relativa de deslizamiento y humedad del suelo, (Persson, 1998). Por otro lado la determinación de las propiedades físicos mecánicas del suelo resultan una etapa indispensable ya que constituyen elementos de entrada para la evaluación de los métodos teóricos que se elaboren y pueden variar en dependencia del tipo de suelo y material en contacto presentando variaciones regidas por leyes estadísticas (García de la Figal, 1978).
Por tal motivo resulta necesario desarrollar una investigación que permita establecer un método experimental adaptado a las condiciones de un suelo ferralítico rojo, típico de la agricultura cubana que caracterice la variación del coeficiente de fricción dinámico suelo-metal en función de la velocidad relativa de deslizamiento, humedad volumétrica y presión específica del suelo. Aspecto que no está lo suficientemente abordado en la literatura desde el punto de vista de los valores y del método aplicado.
MÉTODOS
Empleando el método de la mecánica clásica con el criterio la ley de Amontón para el rozamiento seco según García de la Figal (2010), se determinó el valor del coeficiente de fricción dinámico suelo metal (μd) partiendo de la fuerza de tiro (f) obtenida de un transductor de fuerza tipo S y la fuerza normal (N), asumiendo que la velocidad de deslizamiento es constante (Figura 1), siendo la acción de las fuerzas de inercia igual a cero. Considerando al coeficiente de fricción dinámico suelo-metal (μd) constante e igual a f/N = Ff/N, durante un estado estable de deslizamiento.
Se hizo deslizar un conjunto plancha metálica-masa calibrada de material CT-3 con acabado superficial basto de 15 x 17 mm y espesor de 2 mm, sobre un suelo Rhodic Ferrasol, franco arcilloso limoso, proveniente de la zona agrícola de San José de las Lajas colocado en el canal de suelo del Centro de Mecanización Agropecuaria (CEMA).
Planificación del experimento
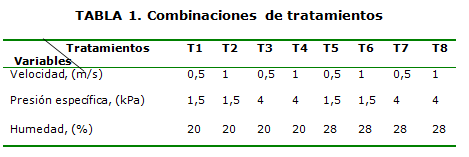
Como variable dependiente se estableció el coeficiente de fricción dinámico suelo metal (μd), y se establecen tres variables independientes: velocidad de deslizamiento (V), humedad volumétrica (H) y presión específica (P) sobre el suelo con dos niveles de variación para cada uno: un nivel bajo y otro alto. Se define un diseño de naturaleza factorial 32 para un total de 9 tratamientos con 3 repeticiones, totalizando 27 corridas experimentales (Tabla 1). Para las corridas experimentales aleatorizadas se agruparon los tratamientosT1-T5, T2-T6, T3-T7 y T4-T8 atendiendo a utilizar una misma velocidad de deslizamiento en cada corrida experimental.
El suelo se preparó sin destruir su textura y estructura donde fueron desterronadas y eliminadas las gravillas, compactado con un cilindro de masa 345 kg y nivelado con un perfil rectangular de aluminio de 2 m de longitud y comprobado con un nivel de burbuja de 1 m de longitud con una precisión de 0,258o (Figura 2).

Se dividió el canal en cinco secciones de 1 m de longitud con un tacómetro digital modelo SHIMPO de una precisión de 0,01 m siendo la intermedia dividida a la mitad por una plancha de madera colocada a nivel superficial para controlar dos niveles de humedad a ambos lados en cada corrida experimental con tres repeticiones (Figura 3).

Los niveles de humedad se obtuvieron con cantidades de agua por unidad de superficie en el orden de 10 y 15 L/m2 respectivamente y su controló utilizando el método de reflectometría de dominios magnéticos del tiempo (TDR), logrando una distribución uniforme de la humedad a las 24 h.
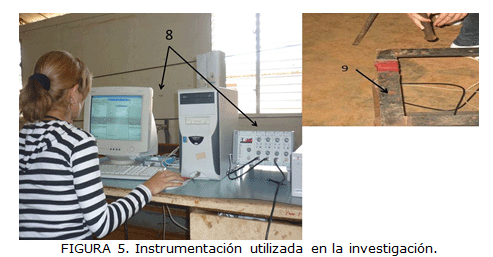
El conjunto plancha metálica-masa calibrada se deslizó con la ayuda de una instalación (Figura 4) formada por un accionamiento electro-mecánico (1-2-3), motor eléctrico (1), tambor motriz (4) y un cable (5) que tiró del conjunto plancha metálica-masa calibrada (6). La fuerza de tracción se midió con el transductor de fuerza tipo S (7). La señal se registró con el sistema de análisis y adquisición de datos dinámico (8) y para delimitar el paso por cada sección del conjunto plancha metálica-masa calibrada se utilizó un sistema tensométrico (9) como señal de referencia (Figura 5).
La velocidad de deslizamiento se determinó como el cociente de la longitud de la sección y el tiempo que demora el conjunto plancha metálica-masa calibrada en atravesarla. La señal de referencia emitida por un transductor tensométrico (9) fue obtenida del software YE 7600.
El procesamiento estadístico se realizó aplicando un análisis de varianza (ANOVA) presentando el indicador del nivel de significación (el p-valor del test F).y para el procesamiento de los datos se emplean los programas Estatgraphics plus, versión 5.1 (en español) y Excel 2011. El número de muestras para la realización de los diferentes ensayos experimentales, se determina a partir de un pre-experimento realizado por Valdés (2008), y para cada variable se obtuvieron los estadígrafos siguientes: media aritmética, desviación estándar, intervalo de confianza según una distribución de la t student y el error relativo.
RESULTADOS Y DISCUSIÓN
El pre-experimento realizado para una humedad del suelo de 20,5%, presión especifica 3,843 kPa y velocidad de deslizamiento 0,579 m/s estableció como 90 el número mínimo de muestras a tomar. En todas las corridas experimentales se utilizaron tamaño de muestras por encima de las 250.
Los valores de la media aritmética de la humedad volumétrica del suelo (Tabla 2) en la sección 1-2 es igual a 20,538 % y para la sección 4-5, igual a 26,138%. El mayor valor del error relativo obtenido en los experimentos realizados, tanto para una probabilidad del 99% o un 90% en el intervalo de confianza, se encuentran en el entorno del 5%, lo cual según criterio de expertos se considera muy aceptable. Puesto que el indicador del nivel de significación (p-valor del test F) obtenido resulta inferior a 0,05, existe diferencia estadísticamente significativa entre los dos niveles de humedad obtenidos.
Los estadígrafos obtenidos del análisis descriptivo realizado a los valores de velocidad de las corridas experimentales (Tabla 3) muestran que la media aritmética correspondiente al nivel bajo resultó igual a 0,673 m/s y para el nivel alto resulto ser de 1,234 m/s. Para un intervalo de confianza con una probabilidad del 99 % el error relativo obtenido fue superior al 10% lo que se explica por la alta variabilidad de regulación de la fuente de suministro del voltaje del motor de corriente directa. Para una probabilidad del 90 % en el intervalo de confianza, el error relativo se encuentra en el entorno del 10% lo que se considera aceptable. El indicador del nivel de significación (p-valor del test F) obtenido resulta inferior a 0,05, existiendo diferencia estadísticamente significativa entre los dos niveles de velocidad.

En la Figura 6 se muestra los valores del coeficiente de fricción dinámico suelo-metal obtenidos en cada tratamiento en función de las variables independientes (velocidad, humedad y presión específica) el cual varía en un rango desde 0,57 hasta 0,82.
Se realizó la comparación de 28 combinaciones de tratamientos de los cuales 16 combinaciones presentaron diferencias estadísticamente significativas en la variabilidad del coeficiente de fricción dinámico según el análisis de varianza realizado. Así mismo se realizó dicho análisis para determinar la variabilidad de las variables independientes estudiadas por combinación de tratamiento, lo cual arrojó diferencias estadísticamente significativas en: 16 combinaciones para presión especifica, 19 combinaciones para la velocidad de deslizamiento y 16 combinaciones para la humedad volumétrica.
Las influencias de las variaciones de las variables independientes en la variación significativa del coeficiente de fricción dinámico, según cada combinación de tratamiento son: la presión específica influye en las 16 combinaciones; la humedad volumétrica en ocho (8) de 16 y la velocidad de deslizamiento en siete (7) combinaciones de 19.
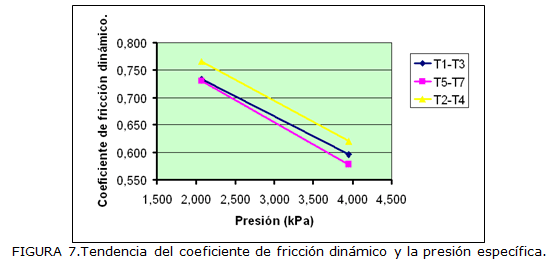
En la Figura 7 se aprecia como el coeficiente de fricción dinámico tiende a disminuir a medida que aumenta la presión, lo cual es posible explicarlo sobre la base de que a una menor deformación de los agregados de suelo (granos y coloides) producto de una menor presión se invierte mayor gasto de energía en poner en movimiento los agregados del suelo. Resultados similares fueron obtenidos por Nichols (1925), Schuchin (1949), Yakovenko (1951), citados por García de la Figal (2010), para otros tipos de suelos.
El coeficiente de fricción dinámico presentó una tendencia similar a la obtenida anteriormente donde este disminuye con el aumento de la velocidad independiente del nivel de presión que se encuentre aplicado en el suelo (Figura 8). El rango del coeficiente de fricción oscila entre 0,73 y 0,76 para un nivel de presión específica de 2,068 kPa y para una presión específica de 3,951 el rango del coeficiente de fricción oscila entre 0,575 y 0,620. Resultados similares fueron obtenidos por Nichols (1925), Schuchin N. (1949), Yakovenko A. (1951), citados por García de la Figal (2010), para otros tipos de suelos.
CONCLUSIONES
Se obtuvieron 16 combinaciones de tratamientos en los cuales el coeficiente de fricción dinámico presentó diferencia estadísticamente significativa, donde la presión específica incide en las 16 combinaciones, la humedad volumétrica en 8 y la velocidad de deslizamiento en 7.
Los valores del coeficiente de fricción dinámico se encuentran entre 0,57 y 0,82 en función de las variables independientes estudiadas (velocidad, humedad y presión específica).
El coeficiente de fricción dinámico manifiesta una tendencia de aumentar a medida que disminuye la presión específica sobre el suelo, debido a que se invierte mayor gasto de energía en poner en movimiento los agregados del suelo.
El coeficiente de fricción dinámico presentó una tendencia a aumentar a medida que: disminuye la presión específica sobre el suelo; aumenta la velocidad inicialmente desde 0,59 hasta 0,9 m/s y, posteriormente, tiende a mantenerse constante hasta valores de 1,73 m/s para un nivel de presión bajo (2,068 kPa) y una tendencia a disminuir para un nivel de presión mayor (3,951 kPa).
REFERENCIAS BIBLIOGRÁFICAS
1. BAUMBERGER, T.: Dry friction dynamics at low velocities, Physics of sliding friction, pp. 1-26, Kluwer, Dortrecht, Ed. B.N.J. Persson, E. Tosatti, The Netherlands, 1996.
2. BEER, P.F. ; RUSSELL J. E. JR.: Mecánica vectorial para ingenieros, McGraw-Hill, México, 1990.
3. MENDEZ URQUIDEZ, B. C.: Investigación experimental de la fricción dinámica en una interfaz madera sobre madera, 135pp., Tesis (en opción al título de Maestro en Ingeniería Geotecnia), Ciudad Universitaria, México, D.F. 2004.
4. GARCÍA DE LA FIGAL, C., A.: Estudio de la fricción suelo-metal y suelo-plástico para dos suelos cañeros cubanos, ISPJAE, La Habana, Cuba, Ciencias Técnicas, Ingeniería en Construcción de Maquinaria, 3: 107–122, 1978.
5. GARCÍA DE LA FIGAL, C., A.: Análisis de fricción suelo metal y plástico antifricción, 21pp., Universidad Agraria de La Habana, Facultad de Mecanización, La Habana, (material digital), 2010.
6. PERSSON, B. N. J.: Sliding friction: physical principles and applications, Berlin, Springer, Germany, 1998.
7. SHIGLEY, J. E. Diseño en Ingeniería Mecánica, McGraw-Hill Interamericana de México, S.A. de C.V. Inc., México, 1990.
8. VALDÉS HERNÁNDEZ, P.A. Modelación físico-matemática del proceso tecnológico del órgano de corte de tambor en las picadoras de forraje con alimentación manual, 186pp.Tesis (en opción al grado científico de Doctor en Ciencias Técnicas Agropecuarias), Universidad Agraria de La Habana, San José de las Lajas, La Habana, 2008.
9. WOLFGANG, E.: Friction measurements in granular media, Physical Review E 69, 021303 pp.10. USA, 2004.
10. YUSU, Y. ; Z, DECHAO: Investigation of the relationship between soil-metal friction and sliding speed, Journal of Terramechanics, 27(4): 83-290, 1990.
Recibido: 17 de diciembre de 2010.
Aprobado: 19 de mayo de 2012.
Ernesto Ramos Carbajal, Universidad Agraria de La Habana, Facultad de Ciencias Técnicas, Centro de Mecanización Agropecuaria, San José de las Lajas, Mayabeque, Cuba, Correo electrónico: carbajales@isch.edu.cu
 Citado por SciELO
Citado por SciELO  Similares en
SciELO
Similares en
SciELO 


















