Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Ciencias Técnicas Agropecuarias
versión On-line ISSN 2071-0054
Rev Cie Téc Agr vol.24 no.3 San José de las Lajas jul.-set. 2015
ARTÍCULO ORIGINAL
Predicción de la resistencia del suelo durante la labranza mediante los modelos de presiones pasivas
Predicting soil resistance during tillage by means of models of passive pressures
Dr.C. Miguel Herrera SuárezI, Dr.C. Ciro E. Iglesias CoronelII, Mg. Cesar Jarre CedeñoI, Ing. Yuriel León SilverioIII, Dr. C. Elvis López BravoIII, Dr. C. Omar González CuetoIII
I Universidad Técnica de Manabí, Facultad de Ing. Agrícola, Portoviejo, Manabí, Ecuador.
II Universidad Agraria de La Habana, Facultad de Ciencias Técnicas, Mayabeque, Cuba.
III Universidad de Central de Las Villas. Dpto. Ing. Agrícola, Santa Clara, Villa Clara, Cuba.
RESUMEN
Para la explicación de los mecanismos que originan la falla del suelo cuando es interactuado por una herramienta de labranza y la predicción de esfuerzos, se han desarrollado más de cincuenta modelos analíticos, alcanzando la mayor aceptación los que se basan en la teoría de las presiones pasivas del suelo. Por tal motivo, el presente trabajo tiene como objetivo determinar la exactitud de cuatro modelos que se basan en la ecuación universal del movimiento de tierra, durante la labranza de un Rhodic Ferralsol del occidente de Cuba. Para lo cual se determinó experimentalmente la resistencia del suelo durante la labranza en las condiciones controladas del canal de suelos CS-CEMA-25, y se programaron las secuencias de cálculo de los modelos Godwin & Spoor; McKyes & Ali; Grisso et al, en el software Mathcad 15. Los principales resultados mostraron las limitaciones de estos modelos para predecir con exactitud los esfuerzos que surgen durante la labranza en suelos altamente cohesivos, así como para herramientas que difieran de la geometría para los cuales originalmente fueron desarrollados. Se demostró además que existe una alta correlación (r=0,90 a 0,98) entre los valores predichos por estos modelos, evidenciando la semejanza en los criterios teóricos que los fundamentan. Por otra parte observó que la velocidad de avance del órgano de trabajo tiene muy poca incidencia en la exactitud de las predicciones de los modelos investigados.
Palabras clave: ecuación universal del movimiento de la tierra, ángulo de fricción, espiral logarítmica, método de las cuñas.
ABSTRACT
For the explanation of the mechanisms that originate the failure of the soil when it is interacted for a farm tool and the prediction of efforts have been developed more than fifty analytic models, reaching the biggest acceptance those that are based on the theory of the passive pressures of the soil. For such a reason, the present work has as objective to determine the accuracy of four models that are based on the universal equation of the soil movement, during the farming of a Rhodic Ferralsol of the occident of Cuba. Was determined experimentally the resistance of the soil during the tillage under controlled conditions in the channel of soils CS-CEMA-25, and were programmed the sequences of calculation of the models Godwin & Spoor, McKyes & Ali,; Grisso et al., in the software Mathcad 15. The main results showed the limitations of these models to predict with accuracy the efforts that arise during the farming in highly cohesive soils, as well as for tools that differ of the geometry for those which originally were developed. It was also demonstrated that a high correlation (r=0.90 to 0.98) exists among the predicted values for these models, evidencing the likeness in the theoretical approaches that base them. On the other hand was observed that the speed of advance of the working tool has very little incidence in the accuracy of the predictions of the investigated models.
Key words: universal equation of the movement of the soil, angle of friction, logarithmic spiral, method of the wedges.
INTRODUCCIÓN
La necesidad de investigar el funcionamiento de los aperos de labranza da lugar al surgimiento de dos escuelas a principio del siglo pasado (1927), las cuales se basaron en el desarrollo de métodos teóricos y experimentales, siendo Goriatchkin y Nichols los pioneros o iniciadores de las mismas (Shen y Kushwaha, 1998). A partir de estos estudios muchas investigaciones han sido conducidas mediante métodos experimentales o teóricos. Los primeros por lo general se desarrollan directamente en el campo, en las condiciones naturales de las zonas a estudiar en cuestión, o en laboratorios diseñados para este tipo de estudios (Hemmat et al., 2013; López, 2013; Munkholm et al., 2013; Schjønning y Thomsen, 2013). Tienen como ventaja la posibilidad de obtener experiencia sobre el funcionamiento y la evaluación de los diferentes aperos de labranza, aunque su principal desventaja radica en la gran cantidad de recursos (financieros, materiales, humanos) que se necesitan para la realización de las investigaciones. Los métodos teóricos se soportan en el empleo de los métodos analíticos o numéricos. Los primeros han sido empleados extensivamente en la predicción de los esfuerzos actuantes sobre los aperos de labranza, para condiciones estáticas o dinámicas, dando lugar al surgimiento de una gran cantidad de teorías para la predicción de los esfuerzos durante la labranza del suelo (Godwin & Spoor, 1977). Tienen como ventaja la sencillez para calcular los esfuerzos y las deformaciones del suelo una vez que se conoce su exactitud. Su principal limitación radica en que por lo general la validez de los mismos se restringe a las condiciones de los suelos donde fueron desarrollados.
Los métodos numéricos han alcanzado gran expansión en las últimas tres décadas, producto del aumento de la potencia y la disponibilidad que han tenido los medios de computo, destacándose el método de elementos finitos y el de elementos discretos en cuanto a su exactitud y utilización (Bentaher et al., 2013; Chen et al., 2013; Li et al., 2013; López, 2013; Ono et al., 2013; Tamás et al., 2013; Zhu y Jia, 2014), sus principales limitaciones se centran en el recurso computacional que demanda esté método y en conocimiento previo que se debe tener para su utilización.
A partir de los métodos analíticos, se han desarrollado varios modelos tridimensionales (3D) y bidimensionales (2D) para la predicción de los esfuerzos durante la labranza, tanto para herramientas estrechas como anchas. Los modelos más utilizados en el ámbito internacional son los que se basan en la teoría de las presiones pasivas del suelo, tomando como base la ecuación universal del movimiento de la tierra propuesta en 1965 por Reece, (Shen y Kushwaha, 1998). Dentro de estos, los más utilizados son los de Godwin y Spoor (1977); McKyes y Ali (1977); y el de (Grisso et al., 1980).
A pesar de la gran aceptación de los mismos en el ámbito internacional y de las ventajas que brindan para la determinación de los esfuerzos durante la labranza, en Cuba, aun no se reportan aplicaciones de estos, desconociéndose su validez o exactitud en las condiciones de los suelos agrícolas cubanos.
Tomando en cuenta estos aspectos el objetivo del presente trabajo es: investigar en condiciones de laboratorio la validez de los modelos de fallas del suelo que se basan en la teoría de las presiones pasivas.
MÉTODOS
La investigación experimental desarrollada con el fin de determinar los esfuerzos que surgen durante la labranza, se realizaron en las condiciones controladas del canal de suelos CS-CEMA-25, del Centro de Mecanización Agropecuaria (CEMA) de la Universidad Agraria de La Habana, (Figura. 1). Sus características técnicas han sido descritas con anterioridad por Herrera et al. (2011). Como órgano de trabajo, se empleó un escarificador alado el cual fue construido en el taller de prototipos del CEMA.
Preparación y acondicionamiento del suelo contenido en el canal. El procedimiento para el acondicionamiento del suelo contenido en el depósito de suelo del canal, siguió una secuencia que garantizó el desmenuzamiento, humedecimiento y compactación del mismo.
Desmenuzamiento del suelo: El desmenuzamiento del suelo se realizó con la ayuda de un cultivador tipo escardillo, acoplado al carro portaherramientas, el mismo posibilitó la descompactación y mullido del suelo hasta la profundidad de 0,30 m. El desmenuzamiento de los 0,80 m de ancho total del canal, se logró variando la posición del bastidor que soportó el escardillo con respecto a su posición central del carro. Cuando no se alcanzó el grado de desmenuzamiento requerido por este medio, se pasó al desmenuzamiento manual con la ayuda del tridente y la guataca.
Humedecimiento del suelo: Para establecer la humedad del suelo requerida en cada experimento se empleó una regadera manual, a la cual se le adicionó un contador de flujo para controlar el flujo de agua suministrado en un intervalo de tiempo dado. La uniformidad de riego se garantizó subdividiendo el depósito de suelo en 8 partes iguales, de 3 m cada una. Finalmente este se tapó con una banda de nylon durante 24 h, para garantizar la homogenización de las condiciones de humedad del suelo.
Compactación del suelo: En los ensayos que se requería el suelo compactado se acopló un rodillo al carro porta herramientas, el cual posibilitó la compactación del suelo de forma mecanizada. Se realizaron tantos pases de rodillo como fueron necesarios para garantizar la magnitud de la compactación requerida.
Determinación experimental del sistema de fuerzas actuantes sobre el órgano de trabajo. Para la determinación de las fuerzas actuantes sobre el órgano de trabajo (Reacción del suelo) se recurrió al empleo de la extensometría electrónica, para lo cual se utilizó un sistema de adquisición y almacenamiento de datos integrado, por:
• Transductor ortogonal de anillos extendidos, para la determinación de las reacciones del suelo sobre el órgano de trabajo (Figura. 2a);
• Amplificador de señales KYOWA de seis canales, (Figura. 2b);
• Tarjeta de conversión analógica digital;
• Computadora personal Pentium IV con procesador a 1,5 GHz, 500 MB de menoría RAM y 40 HB de disco duro (Figura. 2b).
La computadora controló el sistema mediante un software (Tensoft), el cual posibilitó la adquisición, almacenamiento, visualización y graficación de los datos registrados.
Determinación experimental de la velocidad de avance de la herramienta de labranza. Esta variable se midió con ayuda del sensor de velocidad acoplado en la rueda trasera del carro porta herramientas (Figura 3). Su principio de funcionamiento ha sido ampliamente descrito en otros recursos (Herrera et al., 2011; Lara et al., 2011).
Planificación de los experimentos. Para determinar la validez de los modelos en diferentes condiciones de humedad y densidad de suelo, así como, de las velocidades de trabajo, se definieron como variables independientes (Xi): X1, velocidad de trabajo (V), km·h-1; X2, humedad del suelo (W), %; X3, densidad aparente del suelo (gd), g·cm-3.
Como variable dependiente (Yi), se definió: Y1, reacción del suelo al corte de la herramienta de labranza en el eje x (Rx), kN.
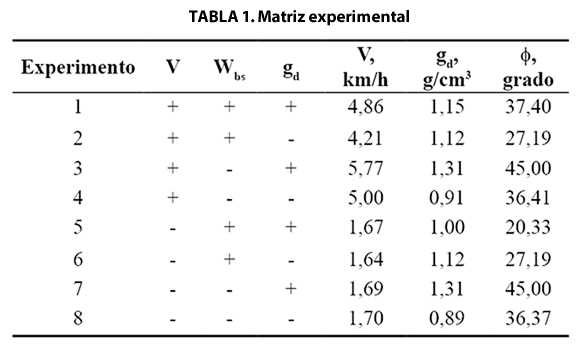
Se realizaron ocho experimentos, en los cuales las variables humedad y densidad se tomaron, considerando dos estados fundamentales del suelo para cada variable (húmedo o seco; suelto o compacto), a partir de lo cual se establecerán las diferentes combinaciones de estas variables, según la matriz experimental mostrada en la tabla 1. Sus valores absolutos en cada condición dependieron del estado del suelo en el momento de la experimentación.
Durante la experimentación se dividió el canal de suelos en partes iguales (12,5 m), con el fin de garantizar la mayor homogeneidad posible del suelo entre los experimentos que poseen las mismas condiciones de suelo, pero diferente velocidades de trabajo. Los experimentos con velocidades más altas se realizaron en la primera mitad del canal. Al concluir estos se retrocedió el carro portaherramientas una distancia prudencial (≈3m) en función de garantizar la estabilidad de la velocidad de trabajo en el experimento siguiente.
El orden de ejecución de los experimentos comprendió que inicialmente se realizaran las corridas 4 y 8, en las cuales el suelo se encontraba en estado seco y suelto, los diferentes niveles de velocidad se garantizaron cambiando los sproket en la transmisión. Posteriormente en el mismo día e inmediatamente después de la primera corrida se pasó el rodillo compactador para alcanzar el nivel máximo de densidad del suelo previsto (experimentos 3 y 7).
Una vez realizadas las corridas correspondientes nivel bajo de humedad del suelo, se inició su descompactación y desmenuzamiento, para posteriormente humedecerlo hasta alcanzar humedad alrededor de 35%. A partir de esto se tapó el depósito de suelo con la banda de nylon 5 días para homogenizar humedad del suelo. Finalmente se iniciaron las corridas correspondientes a los niveles máximos de la humedad del suelo, siguiendo la secuencia anteriormente descrita hasta completar las corridas previstas en la matriz experimental (Tabla 1).
Metodología para la determinación de las condiciones del suelo
El muestreo para la determinación del estado de humedad y compactación del suelo, se realizó de forma tal, que se atenuaron los posibles efectos de borde, pues se desecharon 0,50 m en ambos extremos del canal, así como entre las fronteras que delimitan la mitad del canal, es decir la zona de culminación e inicio de experimentos con condiciones de suelo comunes pero con diferentes velocidades de avance del órgano de trabajo. Las mismas se tomaron en la zona su zona de acción directa, para dos niveles de profundidad (0,10 y 0,20 m).
La recolección de las muestras se realizó antes del paso del órgano de trabajo. El número de muestras en cada experimento (5), se determinó según el criterio de Student.
Metodología para determinar la humedad del suelo: El método empleado fue el gravimétrico, con secado en la estufa a 60 °C de temperatura durante 24 horas, hasta alcanzar una masa constante. El valor de la humedad se calculó mediante la siguiente expresión:
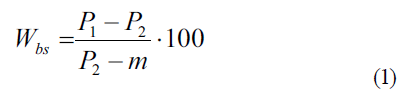
donde: Wbs, humedad del suelo, %; P1, masa del suelo húmedo dentro del recipiente, g; P2, masa del suelo seco dentro del recipiente, g; m, masa del recipiente sin muestra, g.
Metodología para determinar la densidad aparente del suelo: Para su determinación se empleó el método de los cilindros de Kopecki. El método de secado de las muestras de suelo fue el mismo descrito para la humedad del suelo.
Finalmente la densidad se calculó, como:

donde: gd-densidad aparente del suelo, g·cm-3; Gn, masa del suelo después de secada, g; Vc, volumen del cilindro para la toma de muestras, cm-3.
Implementación de los modelos en la herramienta computacional. Se programaron las ecuaciones comprendidas en los modelos de Godwin y Spoor (1977); McKyes y Ali (1977); Grisso et al. (1980), en el software Mathcad 15. Se describió el problema a modelar, y se definieron los modelos geométricos que representaron en forma idealizada la interacción suelo-apero de labranza, se declararon además las propiedades mecánicas requeridas como datos de entrada por los modelos objeto de estudio.
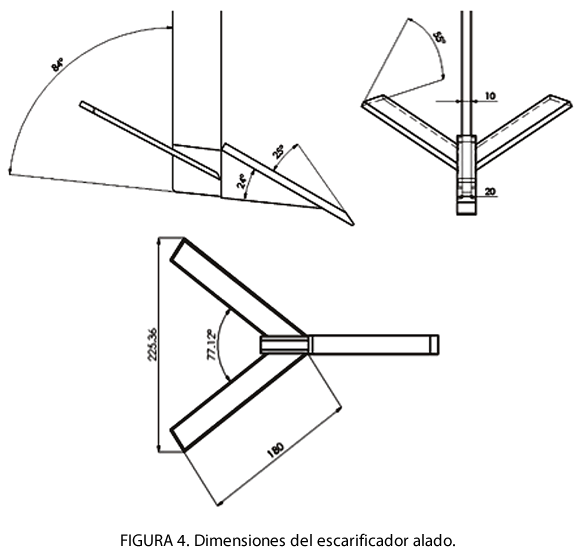
Descripción del problema objeto de modelación. El problema objeto de modelación comprendió el corte del suelo por una herramienta de labranza del tipo escarificador alado (Figura 4), la cual fue considerada como un herramienta estrecha, pues la relación profundidad ancho de trabajo fue d/w= 0,89, es decir la profundidad de trabajo fue mayor que el ancho de trabajo.
Para la implementación de los modelos se tomaron en cuenta las siguientes consideraciones:
• El suelo que es interactuado por la herramienta, se consideró como un suelo isotrópico y homogéneo;
• El suelo cortado después de la falla se desliza por encima de la superficie de la herramienta a una velocidad constante;
• El modelo incluyó parámetros que definieron la cohesión y la fricción del suelo;
• La presencia de una interface suelo-herramienta, se definió por el ángulo de fricción externa (suelo-herramienta);
• La falla del suelo se describió mediante el modelo de Mohr-Coulomb;
• La densidad del suelo no se afecta durante la acción de la herramienta de labranza;
• No se tomaron en cuenta las fuerzas de aceleración del suelo en la herramienta de labranza.
Definición del modelo geométrico. Representaron en forma idealizada un escarificador alado que interactúa con el suelo. Durante esta acción se definieron dos regiones dentro del área de suelo disturbada (Figura 5), es decir el suelo removido por la acción directa de la reja y el suelo disturbado por la acción de las saetas laterales. Hay momentos en que se solapa la acción de ambos elementos.
Tomando en cuenta los basamentos teóricos de cada modelo, la acción de la reja y de las saetas laterales en la definición de los modelos comprendió dos variantes fundamentales, siendo:
Variante I. En el modelo se idealizó la herramienta de labranza considerando la acción independiente de la reja y las saetas que están dispuestas 0,0062 m por encima de la punta de la reja, es decir se computaron de forma independiente los efectos de la reja y las saetas (Figura 5). La zona de donde se solapa la acción de la reja y la saeta lateral se tomó como la acción de la sobrecarga del suelo, a la hora de calcular las fuerzas ejercidas por la saeta. Tanto la reja como las saetas provocan la falla de la cuña central del suelo, además de la falla lateral (Godwin y Spoor, 1977; McKyes & Ali, 1977).
Variante II. Esta variante tomó en cuenta las mismas consideraciones que la variante anterior con la diferencia que el suelo cuando es sometido a la acción de la saeta y la reja, no falla lateralmente, solo se observa una falla central, según la teoría descrita en el modelo de Grisso et al. (1980).
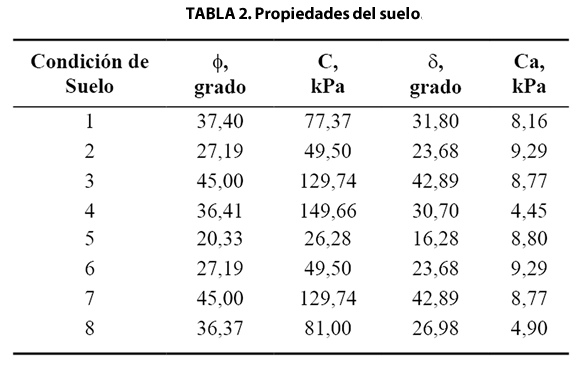
Propiedades mecánicas del suelo requeridas por los modelos. Los valores de las mismas fueron determinados en función del estado de humedad y densidad de cada experimento, mediante las ecuaciones empíricas desarrolladas por Herrera et al. (2008a,b) (Tabla 2).
donde: W, humedad; gd, densidad seca; ф, ángulo de fricción interna; C, cohesión; δ, ángulo de fricción suelo-metal; Ca, adhesión.
RESULTADOS Y DISCUSIÓN
Propiedades mecánicas del suelo requeridas por los modelos
En la Tabla 3, se muestran las características físicas del suelo contenido en el canal, el cual se clasifica como un Rhodic Ferralsol (FAO-UNESCO, 1988); Oxisol según USDA (Soil Survey Staff, 2010); y como Ferralítico Rojo Típico según la tercera clasificación genética de suelos en Cuba (Jiménez, 1999). Según su textura se puede considerar como una arcilla loamosa muy plástica.
donde: LP, límite plástico; LL, límite líquido; IP, índice de plasticidad; S, varianza; S2, desviación estándar; e, error estándar; CV, coeficiente de variación.
Resultados de la estimación de los esfuerzos por los modelos en estudio
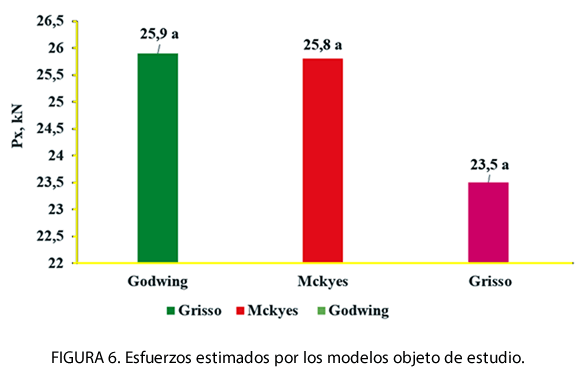
Los resultados evidenciaron (Figura 6), que los valores estimados por los modelos no mostraron diferencias estadísticamente significativas entre sí, para un 95% del nivel de confianza, lo cual es un indicador de la uniformidad en los criterios teóricos que fundamentan dichos modelos (Ecuación universal del movimiento de tierra). Los valores de la resistencia del suelo predichos dependieron directamente de las condiciones del suelo y operación del apero.
Según la configuración adoptada por los modelos, la mayor parte de la fuerza demandada se debió a la acción de la reja (Tabla 4), pues al estar dispuesta por debajo de las saetas laterales esto propicia que el suelo interactuado por la misma ya se encuentre laborado, y por consiguiente disminuya la demanda tractiva de las mismas. Esta problemática fue observada con anterioridad por Godwin y Spoor (1977) y Spoor y Godwin (1978), concordando en ambos casos que está es la forma más adecuada de calcular los esfuerzos en los aperos alados.
El análisis de los coeficientes empleados por los modelos (Nγ; Nc; Nq), mostró una gran diferencia entre los valores que tomaron los mismos para los diferentes modelos (Tabla 5), haciéndose más significativa esta diferencia para los coeficientes empleados por el modelo de McKyes y Ali (1977), los cuales alcanzaron valores superiores a los mostrados por el resto de los modelos (Tabla 5). No se observó una gran diferencia entre los valores numéricos de estos últimos.
donde: Nγ, factor de la densidad; Nc, factor de cohesión; Nq, factor de sobrecarga; Nca, factor de adhesión; β, ángulo de falla del suelo.
Comprobación experimental de la validez de los modelos
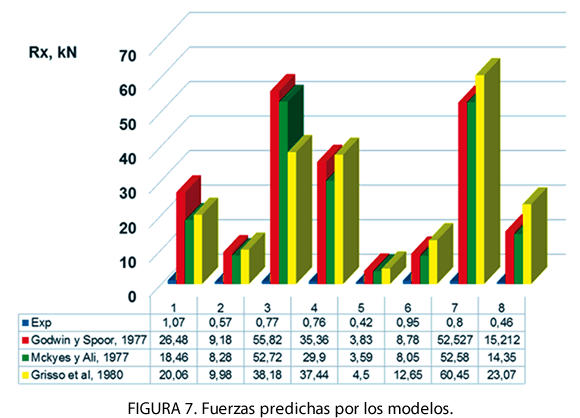
Los resultados experimentales de la determinación de la fuerza de tiro del escarificador alado mostraron que los valores promedios de la resistencia del suelo oscilaron de 0,46 a 1,07 kN, estando los mismos en función de las condiciones del suelo y la velocidad de avance de la herramienta de labranza (Figura 7).
La comparación entre los resultados observados experimentalmente y los predichos evidenciaron que los modelos objeto de estudio sobre predicen considerablemente los resultados experimentales (Figura 7), mostrando diferencias estadísticamente significativas entre los resultados predichos y los experimentales (P=0,014 para un nivel de confianza 1-α=95%), problemática que está dada fundamentalmente por la gran dependencia que tienen estos de la cohesión del suelo, pues el suelo objeto de estudio es altamente cohesivo, sobrepasando los valores de la cohesión de los suelos donde fueron validados originalmente dichos modelos. Este resultado corroboró que la validez de estos modelos se limita a los suelos y condiciones para los cuales fueron desarrollados (Jamshidi et al., 2014).
Las mayor exactitud en las predicciones se encontró (Figura 7), en los experimentos en los cuales el suelo poseía el mayor contenido de humedad (2; 5; 6), independientemente de su estado de densificación o compactación. Sin embargo, los mayores errores en las predicciones se alcanzaron en los experimentos donde el suelo se encontró en estado seco (3; 4; 7), sin evidenciarse un clara influencia del nivel de compactación del suelo en este resultado. Se corroboró, que existe una la elevada incidencia de la magnitud de la cohesión en la exactitud de las predicciones de estos modelos, pues en investigaciones precedentes desarrolladas por Herrera et al. (2008a, b), se demostró que el suelo objeto de estudio (Oxisol) alcanza los máximos valores de la cohesión cuando se encuentra en estado seco, disminuyendo está en la medida aumenta la humedad del suelo.
Por otra parte, se demostró que no existe correlación entre las predicciones y los resultados experimentales (Tabla 6), lo cual es una muestra de las limitaciones de estos modelos al predecir los esfuerzos durante la labranza en suelos altamente cohesivos, como es el caso de los suelos arcillosos cubanos. El análisis evidenció además, la similitud entre los valores predichos por los modelos investigados, fundamentalmente los modelos de Godwin y Spoor (1977) y McKyes y Ali (1977).
CONCLUSIONES
• Los resultados mostraron que los modelos objeto de estudio poseen limitaciones para predecir con exactitud los esfuerzos durante las operaciones de labranza en suelos cohesivos, así como, durante el empleo de herramientas que difieran de la geometría para los cuales originalmente fueron desarrollados;
• Los valores predichos por los modelos tienen poca variación entre sí (r=0,90 a 0,98), encontrándose las menores diferencias entre los de Godwin y Spoor (1977) y McKyes y Ali (1977);
• Los resultados evidencian que la velocidad de avance del órgano de trabajo tiene muy poca incidencia en la exactitud de las predicciones de los modelos investigados.
• Se hace necesario la búsqueda de nuevos coeficientes N, válidos para la estimación de los esfuerzos durante la labranza en suelos altamente cohesivos.
REFERENCIAS BIBLIOGRÁFICAS
1. BENTAHER, H.; A. IBRAHMI; E. HAMZA; M. HBAIEB; G. KANTCHEV; A. MAALEJ; W. ARNOLD: Finite element simulation of moldboard–soil interaction, Soil and Tillage Research, ISSN-0167-1987, (134): 11-16, 2013.
2. CHEN, Y.; L. J. MUNKHOLM; T. NYORD: A discrete element model for soil–sweep interaction in three different soils, Soil and Tillage Research, ISSN-0167-1987, (126): 34-41, 2013.
3. FAO-UNESCO: Soil map of the world, reviewed legend, Report 80, 12pp., Roma. Italia, 1988.
4. GODWIN, R. J.; G. SPOOR: Soil failure with narrow tines., Journal of Agricultural Engineering Research, ISSN 0021-8634, 22 (4): 213-228, 1977.
5. GRISSO, R. D.; J. V. PERUMPRAL; C. S. DESSAI: A soil-tool interaction model for narrow tillage tools. ASAE Paper 80-1518. St. Joseph. MI 49085, pp. 20. 1980.
6. HEMMAT, A.; A. R. BINANDEH; J. GHAISARI; A. KHORSANDI: Development and field testing of an integrated sensor for on-the-go measurement of soil mechanical resistance, Sensors and Actuators A: Physical, ISSN 0924-4247, (198): 61-68, 2013.
7. HERRERA, M. S.; C. E. C. IGLESIAS; O. C. GONZALEZ; E. B. LÓPEZ; A. L. I. SÁNCHEZ: Propiedades mecánicas de un Rhodic Ferralsol requeridas para la simulación de la interacción suelo implemento de labranza mediante el Método de Elementos Finitos: Parte I, Revista Ciencias Técnicas Agropecuarias, ISSN-1010-2760, 17 (3): 31-37, 2008a.
8. HERRERA, M. S.; C. E. C. IGLESIAS; O. C. GONZALEZ; E. B. LÓPEZ; A. L. I. SÁNCHEZ:: Propiedades mecánicas de un Rhodic Ferralsol requeridas para la simulación de la interacción suelo implemento de labranza mediante el Método de Elementos Finitos: Parte II. Interfase suelo-herramienta, Revista Ciencias Técnicas Agropecuarias, ISSN-1010-2760, 17 (4): 50-54, 2008b.
9. HERRERA, M. S.; C. E. C. IGLESIAS; D. C. LARA; O. C. GONZÁLEZ; E. B. LÓPEZ: Desarrollo de un sensor para la medición continua de la compactación del suelo, Revista Ciencias Técnicas Agropecuarias, ISSN-1010-2760, 20 (1): 6-11, 2011.
10. JAMSHIDI, A.; T. MAGHSOUDI; M. S. AGHAPOUR; E. TAYARI: Introduction of modeling a tillage tool on soil (a Review), WALIA journal, ISSN 1026-3861, 30 (1): 12-14, 2014.
11. JIMÉNEZ, A. H.: Nueva versión de clasificación genética de los suelos de Cuba, edit. AGRINFOR, pp. 64, ISBN 9789592460225, 1999.
12. LARA, D. C.; M. S. HERRERA; C. E. C. IGLESIAS: Sensoramiento continuo de la compactación del suelo: revisión y análisis, Revista Ciencias Técnicas Agropecuarias, ISSN-1010-2760, 20 (3): 35-40, 2011.
13. LI, M.; D. CHEN; S. ZHANG; J. TONG: Biomimeitc Design of a Stubble-Cutting Disc Using Finite Element Analysis, Journal of Bionic Engineering, ISSN 1672-6529, 10 (1): 118-127, 2013.
14. LÓPEZ, E.: Simulation of soil and tillage-tool interaction by the Discrete Element Method, 100pp., Tesis en opción al título de Doctor en Ciencias Técnicas Agropecuarias, Faculty of Bioscience Engineering, Catholic University of Leuven, Belgium, 2013.
15. MCKYES, E.; O. S. ALI: The cutting of soil by narrow blades, Journal of Terramechanics, ISSN 0022-4898, 14 (2): 43-58, 1977.
16. MUNKHOLM, L. J.; R. J. HECK; B. DEEN: Long-term rotation and tillage effects on soil structure and crop yield, Soil and Tillage Research, ISSN 0167-1987, (127): 85-91, 2013.
17. ONO, I.; H. NAKASHIMA; H. SHIMIZU; J. MIYASAKA; K. OHDOI: Investigation of elemental shape for 3D DEM modeling of interaction between soil and a narrow cutting tool, Journal of Terramechanics, ISSN 0022-4898, 50 (4): 265-276, 2013.
18. SCHJØNNING, P.; I. K. THOMSEN: Shallow tillage effects on soil properties for temperate-region hard-setting soils, Soil and Tillage Research, ISSN-0167-1987, (132): 12-20, 2013.
19. SHEN, J.; R. L. KUSHWAHA: Soil-Machine interactions: A finite element perspective, edit. Marcel Dekker, Inc, vol. 66, pp. 316, ISBN 0-8247-0145-3, New York-Basel-Hong Kong, 1998.
20. SOIL SURVEY STAFF: Keys to Soil Taxonomy, USDA Natural Resources Conservation Service, 346pp., Washinton, DC, 2010.
21. SPOOR, G.; R. J. GODWIN: An investigation into the deep loosening of soil by rigid tines, Journal of Agricultural Engineering Research, ISSN 0021-8634, (23): 243-258, 1978.
22. TAMÁS, K.; I. J. JÓRI; A. M. MOUAZEN: Modelling soil–sweep interaction with Discrete Element Method, Soil and Tillage Research, ISSN 0167-1987, (134): 223-231, 2013.
23. ZHU, X. H.; Y. J. JIA: 3D Mechanical modeling of soil orthogonal cutting under a single reamer cutter based on Drucker–Prager criterion, Tunnelling and Underground Space Technology, ISSN 0886-7798, (41): 255-262, 2014.
Recibido: 22 de septiembre de 2014.
Aprobado: 19 de abril de 2015.
Miguel Herrera Suárez. Universidad Técnica de Manabí, Facultad de Ing. Agrícola, Av. Urbina y Che Guevara, Portoviejo, Manabí, Ecuador. Correo electrónico: miguelhs2000@yahoo.com
Nota: La mención de marcas comerciales de equipos, instrumentos o materiales específicos obedece a propósitos de identificación, no existiendo ningún compromiso promocional con relación a los mismos, ni por los autores ni por el editor.