Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Ciencias Técnicas Agropecuarias
versión On-line ISSN 2071-0054
Rev Cie Téc Agr vol.24 no.3 San José de las Lajas jul.-set. 2015
ARTÍCULO ORIGINAL
El cambio del módulo de aspersión en pivotes según criterios económicos para Cuba: modelo teórico
The change of the sprinkler irrigation kit in pivots based on economic criteria for Cuba: Theoretical model
Dr. C. Ramón Pérez LeiraI, Dr.C. Jacqueline Domínguez GutiérrezII, Dr.C. Pedro Paneque RondónIII
I Universidad Laica Eloy Alfaro de Manabí (ULEAM) extensión Chone. Manabí, Ecuador.
II Instituto Superior Politécnico José A. Echevarría (ISPJAE), Facultad de Arquitectura, CUJAE, La Habana, Cuba.
III Universidad Agraria de La Habana, Facultad de Ciencias Técnicas, Centro de Mecanización Agropecuaria, San José de las Lajas, Mayabeque, Cuba.
RESUMEN
En este trabajo se presenta un modelo teórico para la determinación del momento óptimo de sustituir el módulo de reguladores de presión y emisores de un pivote. El modelo parte del criterio de que el desgaste en los reguladores de presión y en las boquillas incide en la disminución de la Uniformidad del Riego y este último en la pérdida de rendimientos. Para compensar estas pérdidas se requiere elevar la dosis de riego con vistas a compensar el déficit que se produce en las zonas de mínima entrega lo cual genera in incremento de los costos de explotación. Se consideran en el modelo: los costos por consumo adicional de agua y de energía, por mantenimiento y por mano de obra, así como las pérdidas de rendimiento asociadas a las zonas con riego insuficiente y con riego excesivo. La suma de todos estos componentes es comparada con el costo de la adquisición y montaje de un nuevo módulo de aspersión, lo cual le permite al agricultor decidir el momento propicio para hacer la sustitución a partir de criterios económicos.
Palabras clave: pivote de riego, emisores, modelo, costos, eficiencia.
ABSTRACT
This paper propose a theoretical model for determining the optimal moment to replace the kit of sprinkler irrigation and pressure regulators in a pivot. The model is based that the wear on the pressure regulators and nozzles make the decrease of the Irrigation Uniformity and this causes the yield loss. To compensate these losses an increase of irrigation depth is required to make up the deficit that occurs in areas of low delivery which generates in increased operating costs. Are considered in the model: costs for additional consumption of water and energy, maintenance and labor, and yield losses associated with areas with insufficient irrigation and over irrigation. The set of all these components is compared with the cost of the purchase and installation of a new sprinkler module, which allows the farmer to decide the right moment to make substitutions based on economic criteria.
Key words: pivot irrigation spray, sprinklers, model, cost, efficiency.
INTRODUCCIÓN
La fácil automatización, el bajo requerimiento de fuerza laboral y la posibilidad de utilizar bajas presiones han sido las razones principales que han permitido la rápida extensión del riego con máquinas de pivote central en el mundo (Lyle y Butler, 1980, Bordousky et al., 1992 y Tarjuelo, 1999). En las últimas cuatro décadas han sido numerosos los estudios encaminados a la sustitución de otras técnicas de riego por pivotes y al perfeccionamiento del riego para hacerlo más eficiente y sustentable sobre diversas condiciones de clima, suelo y cultivo. Así surgieron los dispositivos LEPA con un notable incremento en la uniformidad, la eficiencia del riego y un uso más racional de la energía, (Gilley y Mielke, 1980; Glenn et al., 1994 y Tarjuelo, 1999). En los últimos 20 años la escasez de agua y energía han obligado a los diseñadores y agricultores a buscar soluciones alternativas para reducir los consumos asociados al riego de los pivotes. Allen1 realiza un aporte importante a la teoría del diseño hidráulico de los pivotes al incorporar criterios agronómicos al diseño tradicional existente. Una simplificación y transformación de este algoritmo cíclico propuesto por Allen en otro lineal fue realizada por Pérez y Martínez (2004), la cual permitió programarlo y aplicarlo a un caso de estudio.
La mayoría de los estudios sobre la calidad del riego del riego de estas máquinas se apoyan en el coeficiente de uniformidad de Heermann y Hein (1968) a pesar de que Bremond y Molle (1995) demostraron la poca sensibilidad que tiene el mismo en comparación con el Coeficiente de Uniformidad de Variación (CUv) propuesto por ellos. Pérez et al. (2003), luego de evaluar un conjunto de pivotes, concluyeron que un solo indicador no resulta suficiente para dictaminar sobre la calidad del riego y que los factores que más afectan la uniformidad de riego en los pivotes están relacionados con los desperfectos técnicos y el montaje incorrecto de las boquillas y reguladores de presión.
Con respecto a otros difusores, Keller y Bliesner (1990), Kinkaid (1996) y Pérez et al. (2001) concuerdan en las ventajas que proporcionan al riego la colocación de los emisores a 1.0 m en comparación con los instalados a 2,30 m de altura para cualquier espaciamiento en un pivote. Omary y Sumner (2001) a partir de evaluaciones de laboratorio, efectuaron simulaciones en las cuales obtuvieron coeficientes de uniformidad promedio de 98.4%. Faci et al. (2001) encontraron diferencias evidentes entre la calidad de la lluvia producida por boquillas difusoras de deflector fijo con respecto a las de deflector giratorio. Sourell et al. (2003), a partir de simulaciones realizadas a dispositivos de riego tipo Rotator para diferentes condiciones, encontraron Coeficientes de Uniformidad siempre superiores al 87% con un valor promedio de 91.8%. Dukes y Perry (2006) concluyeron por su parte, que el único factor que afectaba significativamente la uniformidad del riego era el tipo de boquilla en dependencia de si el deflector fuera fijo o giratorio.
Ribeiro2 (2001) en un estudio realizado para determinar la vida útil de los reguladores de presión demostró que hasta 6000 horas de uso se mantenía invariable su efecto regulador. Evaldo et al. (2001) determinaron que el Coeficiente de Uniformidad y la dosis de riego disminuyen después que el módulo de aspersión ha sido utilizado por más de seis años. A partir de estas experiencias Pérez et al. (2011) elaboraron un modelo matemático que permite determinar el momento óptimo para el cambio del módulo de aspersión en los pivotes a partir de las condiciones específicas de Brasil.
En Cuba no se han encontrado referencias de este tipo de análisis a pesar de la demostrada reducción que provoca en los orificios y conductos del pivote las incrustaciones del carbonato de calcio presente en el agua. Hasta la fecha no se responde sobre un criterio económico sólido ¿Hasta cuándo es rentable mantener el módulo de aspersión en un pivote después de haber acumulado miles de horas de uso?
Se supone que la disminución de la uniformidad del riego provocada por el desgaste en el módulo de aspersión, obliga al regador a incrementar la dosis de riego bruta para compensar el déficit que se origina en las áreas regadas insuficientemente. Esto incide en el incremento de los costos de operación del riego.
Este trabajo se desarrolla con el objetivo de establecer un modelo teórico que defina los criterios y las variables a considerar para determinar el momento óptimo de cambiar el módulo de reguladores de presión y emisores en un pivote.
MÉTODOS
Para aplicar esta metodología, es preciso que se conozcan los resultados de una evaluación pluviométrica realizada al pivote al comienzo del período de riego con el módulo de aspersores nuevo (o con menos de 2 000 horas de uso). También se requiere del registro de los rendimientos alcanzados por los cultivos que fueron plantados y cosechados, bajo esas condiciones de riego, durante el período de un año. El momento óptimo para el cambio del módulo de aspersión de un pivote se definió a partir de criterios económicos. Para realizar éste análisis se consideró la posible incidencia de los siguientes factores según criterio de Pérez et al. (2011):
Costos fijos
1. Precio del módulo de reguladores de presión y difusores (PMR).
2. Costo de instalación del módulo en el pivote (CIM).
Costos variables
1. Costo por consumo adicional de energía (CCAE).
2. Costo por consumo adicional de agua (CCAA).
3. Costo por consumo adicional de mano de obra (CCAMO).
4. Costo adicional por mantenimiento (CAMT).
5. Costo por pérdidas de rendimiento (CPR).
Si se parte del criterio de que los costos fijos (CF) son un valor constante y de que la suma de todos los costos variables (CV) es la que incide de manera dinámica en la toma de decisiones, se puede plantear que:
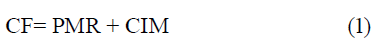
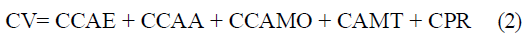
Si se considera para éste análisis que el cambio del módulo sólo es factible económicamente después que se cumpla que CF < CV, entonces se puede plantear que la condición de NO sustitución del módulo de aspersión sería CF ≥ CV, lo cual desglosado en todos sus componentes quedaría:
![]()
A partir de esta inecuación, se procedió entonces a la determinación de cada uno de sus parámetros.
Determinación de los costos fijos
Para la determinación de los costos fijos sólo es necesario considerar las ofertas del proveedor, por lo que serán objeto de análisis solamente en la formulación final de este trabajo.
Determinación de los costos Variables.
Los costos variables fueron determinados a partir de los siguientes criterios:
Costo por consumo adicional de energía (CCAE).
El CCAE fue determinado a partir de la formulación empleada por Pérez et al. (2009) para el consumo del motor eléctrico en la estación de bombeo sumado al consumo del pivote:
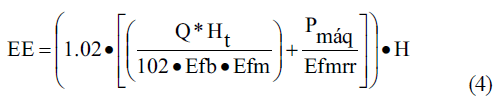
donde:
EE-Consumo eléctrico por riego (kW·h);
Q-Caudal a la entrada del pivote (L/s);
Ht-Carga carga dinámica total (m);
Efb-Eficiencia de la bomba (decimal);
Efm-Eficiencia del motor (decimal);
Pmáq-Potencia demandada por la máquina (kW);
Efmrr-Eficiencia del motoreductor (Efmrr = 0,85);
H-Tiempo total que demora la máquina en aplicar todos los riegos (h).
Sin embargo es necesario conocer el incremento del tiempo de riego por lo que se adoptará la expresión:

donde:
ITr-Incremento de Tiempo de riego (decimales);
TrKv-Tiempo de riego requerido con el Módulo viejo (h);
TrKn-Tiempo de riego requerido con el Módulo nuevo (h). siendo:
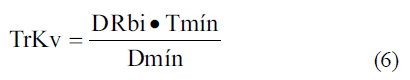
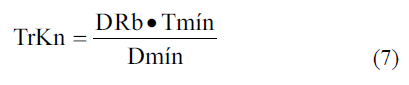
donde:
DRbi-Dosis de riego bruta incrementada para compensar déficit de uniformidad del riego (mm);
DRb-Dosis de riego bruta requerida por el cultivo (mm);
Tmín-Tiempo requerido por el pivote para aplicar un riego a máxima velocidad (h);
Dmín-Dosis mínima de riego aplicada por el pivote a máxima velocidad (mm).
Sustituyendo 6 y 7 en 5 y simplificando quedaría:
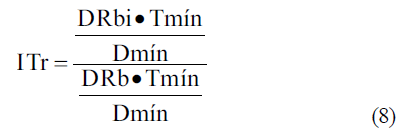
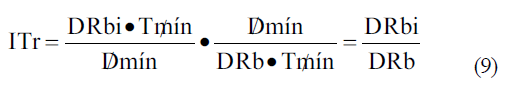
Sustituyendo 9 en 4 se obtiene el consumo eléctrico adicional por riego
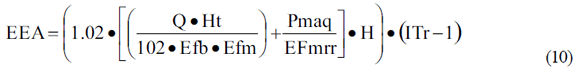
Los costos de demanda y consumo se definen a partir de las tarifas existentes en Cuba.
Con el valor del consumo adicional de riego de la máquina se calcula el costo de la energía eléctrica multiplicando el resultado de la ecuación 10 por las tarifas eléctricas correspondientes a casa horario establecido de riego
![]()
donde:
CCAE-Costo por consumo adicional de energía eléctrica consumida ($, peso);
EEA-Consumo eléctrico adicional por riego (kW·h);
Tarifa - Consumo día (6 AM - 5 PM), $ 0,063/kW·h, Consumo Madrugada (10 PM - 6 AM), $ 0,035/kW·h según la Resolución 311 del Ministerio de Finanzas y Precios (MFP) (2000)3
Sustituyendo la ecuación 10 en la ecuación 11 se obtiene CCAE:
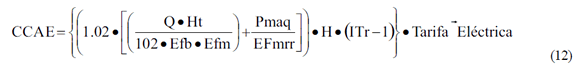
Costo por consumo adicional de agua (CCAA) Al considerar la tarifa establecida en la Resolución 421-2012 emitida por el MFP (2012)4 se plantea la ecuación 13.
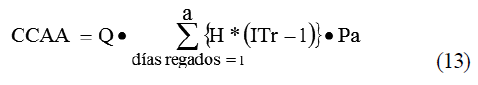
donde:
CCAA-Costo por consumo adicional de agua ($, peso);
Q-Caudal de bombeo requerido por el pivote (m3/h);
Tiempo total de riego (h); a-total de días regados en el año;
Pa-Precio o tarifa de agua de 0.0025 peso/m3 de agua subterránea bombeada según la Resolución 421-2012 emitida por el MFP (2012) y vigente a partir de enero de 2013.
Costo por consumo adicional de mano de obra (CCAMO)
En el cálculo del (CCAMO); se considera el salario medio mensual pagado al obrero agrícola, el número de horas de trabajo necesarios por hectáreas y por riegos realizados.
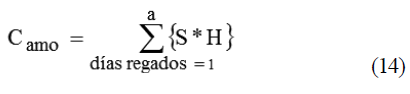
donde:
Camo-Costo anual de mano de obra ($, peso)
a-Total de días regados al año
S-Salario por horas ($ 1,43 horas-1) según López (1990) citado por Pérez et al. (2009)
H-Tiempo total de riego (h)
Al igual que para el caso del costo por consumo adicional de energía es necesario conocer el incremento del tiempo; por lo que se sustituye la ecuación 9 en la ecuación 14.
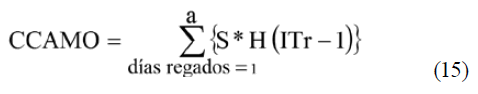
Costo adicional por mantenimiento (CAMT)
Para el CAMT se adoptó como la diferencia entre el costo de mantenimiento del kit viejo y el kit nuevo, obteniéndose entonces:
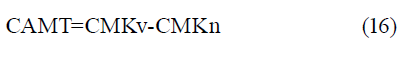
donde:
CMKv-Costo de mantenimiento de los kit viejos ($, peso);
CMKn-Costo de mantenimiento de los kit nuevos ($, peso).
Siendo:

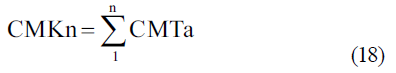
donde:
n-Número de componentes del sistema de riego de pivote central
CMTa-Costo de mantenimiento anual ($, peso)
![]()
donde:
Tm-Tasa anual de mantenimiento;
Ps: Precio de adquisición e instalación del equipamiento de riego ($, peso)
Sustituyendo ecuación 9 en ecuación 17
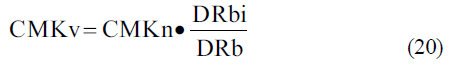
La tasa anual de mantenimiento se estimó a partir de las consideraciones de Pérez et al. (2009)
donde:
TmAF-tasa de mantenimiento de los difusores fijos;
ViAF-valor inicial de los difusores fijos;
TmBC-vasa de tantenimiento de la bomba centrífuga;
ViBC:-valor Inicial de la bomba centrífuga;
TmEB-tasa de mantenimiento de la estación de bombeo (estructura);
ViEB-valor Inicial de la estación de bombeo (estructura);
TmME-tasa de mantenimiento del motor eléctrico;
ViME-valor inicial del motor eléctrico;
TmTA-tasa de mantenimiento de las tuberías de acero galvanizado superficial;
ViTA-valor Inicial de las tuberías de acero galvanizado superficial.
Sustituyendo la ecuación 21 en 19
Sustituyendo la ecuación 20 en 16
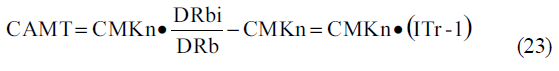
Sustituyendo la ecuación 22 en 18
Sustituyendo ecuación 24 en 23 quedaría:
Al sustituir las ecuaciones 12, 13, 15 y 25 en 3 y adoptar (ITr-1) como factor común se obtendría (26):
A partir de esta expresión general se puede calcular el valor límite a partir del cual los costos asociados a la mala uniformidad justifican el cambio del módulo de aspersión. Para su aplicación real sería preciso conocer la función de rendimiento del cultivo y su precio de venta, así como el costo de instalar un módulo nuevo.
CONCLUSIONES
• El modelo teórico propuesto permite determinar para cualquier cultivo el momento óptimo para el cambio del módulo de aspersión en un pivote. En dicho modelo se consideran los costos variables del pivote, los costos fijos del módulo nuevo y las pérdidas de rendimiento del cultivo.
• Para la aplicación de este modelo es indispensable conocer el valor de la uniformidad de riego del pivote con el módulo de aspersión nuevo bajo condiciones habituales de riego en la región, así como la función de rendimiento y el precio de venta de los cultivos beneficiados con el riego.
Notas al pie
1 ALLEN, R. G.: Applicator Selection along Center Pivots using Soil Infiltration Parameters. Visions of the future, Proceedings of the Third National Irrigation Symposium, ASAE. Phoenix, AZ, 549-555, 1990.
2. RIBEIRO, V.L.S.C.: Avaliação Hidráulica de Válvulas reguladoras de pressão novas e com diferentes tempos de utilização.90pp., Dissertação submetida à coordenação do curso de pós-graduação em Agronomia-Irrigação e Drenagem como requisito parcial para obtenção do grau de mestre, Universidade Federal de Ceará, Brasil, 2001.
3. MINISTERIO DE FINANZAS Y PRECIOS (MFP): Resolución P-6. La Habana, 2000.
4. MINISTERIO DE FINANZAS Y PRECIOS (MFP): Resolución 421-2012. La Habana, 2012.
REFERENCIAS BIBLIOGRÁFICAS
1. AL-KUFAISHI, S. A.; B. S. BLACKMORE & H. SOURELL: "The feasibility of using variable rate water application under a central pivot irrigation system", Irrigation Drainage Systems, [en linea] ISSN: 0168-6291 (Print) 1573-0654 (Online), DOI: 10.1007/s10795-006-9010-2, 20 (2-3): 317-327, 2006.
2. BREMOND, B. & MOLLE, B: "Characterization of Rainfall under Pivot: Influence of Measuring Procedure", Journal of Irrigation and Drainage Engineering, [en linea] http://dx.doi.org/10.1061/ (ASCE) 0733-9437 (1995), ISSN: 0733-9437, 121 (5): 347-353, 1995.
3. BORDOUSKY, J.P.; LYLE, W.M.; LASCANO R, J. & UPCHURCH, D.R. "Cotton Irrigation Management with LEPA systems", Transaction of the ASAE, ISSN: 0001-2351, 35 (3): 879-884, 1992.
4. DUKES, M. D. & C. PERRY: "Uniformity testing of variable-rate center pivot irrigation control systems", Precission Agriculture, [en linea] DOI: 10.1007/s11119-006-9020, Print ISSN: 1385-2256, Online ISSN: 1573-1618, 7 (3): 205-218, 2006.
5. EVALDO K. A; DE CASTRO S. R. & DUROHA, C.: "Evaluation Center Pívot Systems using new and old sprays and pressure regulators". IRRIGA. Brazilian Journal of Irrigation and Drainage, ISSN: 1808-8546, 6 (1): 73-78, 2001.
6. FACI, J. M.; R. SALVADOR; E. PLAYÁN & H. SOURELL. "Comparison of fixed and rotating spray plate sprinklers". Journal of Irrigation and Drainage Engineering, ISSN: 0733-9437, 127 (4): 224-233, 2001.
7. GILLEY J.R.& MIELKE LI.N: "Conserving Energy with Low-Pressure Center Pivot". Journal of Irrigation and Drainage Division: 49-58, 1980.
8. GLENN J.; HOFFMAN & DERREL J.M: "Advanced Irrigation Engineering", International Water Irrigation Review, ISSN: 0044-7978, 14 (2): 24-29, 1994.
9. HEERMANN, D.F. & HEIN, P.R.: "Performance characteristics of self-propelled center-pivot sprinkler irrigation system", Transaction of the ASAE, ISSN: 0001-2351, 11 (1): 11-15, 1968.
10. KELLER, J. & BLIESNER, R.D. Sprinkle and tickle irrigation. AVI Book, ISBN: Van Nostrand Reinhold. New York, 1990.
11. KINCAID D.C.: "Sprinkler Pattern Analysis for Center Pivot Irrigation", Irrigation. Business and Technology: ISSN: 0001-2351, IV (4): 14-15, 1996.
12. LYLE P. & BUTLER G.: "Low energy labor from Texas pivot", Irrigation Farmer, ISSN: 7 (4): 4, 1980.
13. OMARY M. & SUMNER H.: "Modeling Water Distribution for Irrigation Machine with Small Spray Nozzles", Journal of Irrigation and Drainage Engineering, ISSN: 0733-9437, 127 (3): 156-160, 2001.
14. PÉREZ L. R.; DOMÍNGUEZ G.M; CÁRDENAS L. J. F. Y RODRÍGUEZ M. J.: "Boquilla Difusora Cubana: Criterios para el diseño hidráulico de los pivotes", Revista Ciencias Técnicas Agropecuarias, ISSN-p: 1010-2760, ISSN-d: 2071-0054, 10 (1): 79-83, 2001.
15. PÉREZ L. R.; ALFONSO G. E. J.; CÁRDENAS L. J. F.; LÓPEZ C. G. Y ALEMÁN G. C.: "Un estudio de la evaluación de la aplicación del riego en sistemas por pivote central", Ingeniería Hidráulica en México, ISSN: 0186-4076, V. XVIII (3): 45-53, 2003.
16. PÉREZ L. R.; SÁNCHEZ-ROMÁN, R.M Y FRIZZONE, J.A.: "Optimal Moment to Change Pressure Regulator and Sprayer Kit on Center Pivot Irrigation Machines: A Theoretical Proposal", IRRIGA. Brazilian Journal of Irrigation and Drainage, ISSN: 1808-8546,, 16 (4): 436-449, 2011.
17. PÉREZ L. R. Y MARTÍNEZ G. Y. "Simplificación y Adecuación del Método de Allen para determinar el caudal de diseño de los pivotes para el riego del cultivo de la papa", Ingeniería Hidráulica en México, ISSN: 0186-4076, Vol. XIX, No. 2, 2004.
18. PÉREZ L. R.; BERMÚDEZ H., C. Y VALDÉZ M, A.L.: "Costos de operación en los sistemas de riego mecanizado de pivote central", Ingeniería Hidráulica y Ambiental, ISSN: 1680-0338. Vol. XXX, No. 3: 51-60, 2009.
19. SOURELL H.; J. M. FACI; & E. PLAYÁN: "Performance of Rotating Spray Plate Sprinklers in Indoor Experiments". Journal of Irrigation and Drainage Engineering, ISSN: 0733-9437, 123 (5): 376-380, 2003.
20. TARJUELO, J.M.: El riego por aspersión y su tecnología, Ed. Ediciones Mundi Prensa, vol. 3a edición, ISBN: 84-8476-225-4, Madrid, Barcelona, México, 2005.
Recibido: 29 de octubre de 2014.
Aprobado: 19 de abril de 2015.
Ramón Pérez Leira. Universidad Laica Eloy Alfaro de Manabí (ULEAM), extensión Chone. Manabí, Ecuado. Correo electrónico: rperezleira@gmail.com














