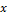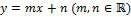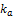Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
Los significados que poseen los profesores sobre un determinado concepto han sido objeto de estudio de las siguientes investigaciones (Radford, 2003; Keitel & Kilpatrick, 2005; Kilpatrick et al., 2005; Silverman & Thompson, 2008; Martín et al., 2016; Byerley & Thompson, 2017). El significado tiene un carácter endógeno y contextual, es decir, no puede ser absolutamente proporcionado, por el contrario, debe construirse fundamentalmente a partir de la experiencia del individuo. Dotar de significado a los objetos matemáticos no puede satisfacerse globalmente ya que, para cada contenido de aprendizaje matemático, el significado debe interpretarse constantemente y construirse subjetivamente. Por lo tanto, al mismo tiempo y en el mismo contexto, los profesores pueden tener diferentes significados del mismo concepto matemático (Kilpatrick et al., 2005).
(Piaget & García, 1991) consideraban que el significado y la comprensión eran sinónimos. Así, dotar de significado un determinado concepto está estrechamente relacionado con su comprensión, es decir, con poder interpretarlo, definirlo, identificarlo y aplicarlo en diferentes contextos. Dotar de significados a los objetos matemáticos permite inferir propiedades más allá de lo que se percibe. El significado, esencialmente, está basado en los esquemas y representaciones que posee la persona (Byerley & Thompson, 2017). Para el presente estudio, las representaciones asociadas con el aspecto operativo del pensamiento son fundamentalmente contextuales y pueden entenderse como un resultado del procesamiento de la información sensorial y conceptual del medio circundante, en la mente del individuo. Ellas se concretan en forma de imágenes, proposiciones e interrelaciones sobre el concepto (Piaget & García, 1991; Moreno, 1996).
En la misma dirección (Thompson, 2013; Thompson 2016; Byerley & Thompson, 2017) estudian los significados que poseen los profesores para el desarrollo de su labor docente, a través de las componentes matemático-cognitivos y didáctico-metodológicos. Así, los significados, resultan ser una combinación de los significados matemático-cognitivos, aquellos que están instituidos o aceptados por la comunidad de matemáticos y los didáctico-metodológicos, que posibilitan la comprensión de cómo se estructuran y adecuan los contenidos, los conceptos, procedimientos, métodos, etc. Esta investigación se centra en el componente matemático-cognitivo del concepto de pendiente en profesores universitarios.
(Barr, 1981; Mcdermott et al., 1987), han identificado dificultades en la compresión del concepto matemático de pendiente, al explorar el concepto de función. De ellas cabe destacar la denominada pendiente-altura, donde la principal dificultad consiste en la confusión de la pendiente de la línea recta con la distancia de un punto de la línea recta al eje horizontal. Según (Zaslavsky et al., 2002), de los profesores que participaron en su estudio sobre los significados de la pendiente, el 47% de ellos presentan predisposición hacia los elementos geométricos, principalmente visuales asociados al concepto y entienden la pendiente como un índice de inclinación. Además, los autores reportan la existencia de confusión entre los aspectos algebraicos y geométricos de la pendiente, la escala y el ángulo.
(Hoffman, 2015) afirma que los profesores consideran preferentemente la interpretación geométrica de la pendiente, ya que el 45% de los encuestados la asocian con la razón geométrica. (Stump, 2001) concluye que menos del 20% de los profesores entrevistados asocian la pendiente con la tasa de cambio de una determinada relación funcional y también observa cierta desconexión entre los conceptos de pendiente y función. Además, plantea que las dificultades y obstáculos relacionados con el concepto de pendiente obedecen básicamente a la utilización sistemática de determinadas acciones u operaciones, sin plena claridad en sus significados y fundamentos. (Nagle et al., 2013) aseveran que las respuestas de un grupo de profesores a tareas relacionadas con el concepto de pendiente, ponen de relieve que dicho concepto apenas es entendido como razón de cambio.
Los significados matemáticos asociados a un concepto, sobre todo son de naturaleza cognitiva, y están en relación con sus características necesarias y suficientes, con la experiencia del individuo y asociado a un determinado contexto (Keitel & Kilpatrick, 2005; Martín et al., 2016; Byerley & Thompson, 2017; Diamond, 2019). Así, los significados nos permiten identificar y clarificar lo que la persona intenta transmitir a partir de una imagen o un enunciado. En función de lo anteriormente expuesto, nos proponemos en lo fundamental, identificar y valorar los significados matemático-cognitivos que poseen los profesores universitarios sobre el concepto de pendiente.
Materiales y métodos
Seguidamente se describe la metodología desarrollada, en un estudio empírico, concebido para explorar el grado en que se manifiestan los significados analítico, algebraico, geométrico y contextual, en profesores de matemáticas. Esta descripción contempla cinco apartados: diseño, instrumentos, participantes, variables y análisis de las evidencias empíricas.
Diseño e instrumentos.
El estudio se estructuró en dos etapas. La primera de ellas consistió en la aplicación de un cuestionario, contentivo de un sistema de problemas relacionados con el concepto de pendiente a un grupo de profesores universitarios que imparten matemáticas. Cabe destacar que este cuestionario fue considerado adecuado para identificar los significados matemáticos del concepto de pendiente en profesores (Sánchez et al, 2021). Los significados asociados al contenido matemático de este concepto lo clasificamos de manera sintética en geométricos, algebraicos, analíticos y contextuales, con las siguientes especificaciones:
Significado geométrico es aquel donde el concepto de pendiente se caracteriza con ayuda de conceptos tales como ángulo de inclinación, razón entre las longitudes de catetos de un triángulo rectángulo formado con dos puntos de una recta y las respectivas diferencias de sus proyecciones, la razón entre el desplazamiento vertical y el desplazamiento horizontal de un punto, entre otros elementos propios del ámbito de la geometría.
Significado algebraico es aquel donde el concepto de pendiente se expresa por intermedio de representaciones relacionadas con la razón de cambio entre valores de ordenada y abscisa de una función lineal. En esencia, el énfasis se pone en calcular el valor de
en la (Ecuación 1) , o bien de calcular mediante la (Ecuación 2):
Significado analítico es aquel donde el concepto de pendiente se relaciona con conceptos tales como la derivada de una función en un punto, la pendiente de la recta tangente a una curva en un punto, el límite de la pendiente de las secantes a una curva en un punto, la razón de cambio instantánea para una función cualquiera, la rapidez de cambio de la función en un punto (la mejor aproximación lineal de una curva en la vecindad del punto es la recta tangente en dicho punto), entre otros elementos del análisis matemático.
Significado contextual es aquel donde se pondera el valor instrumental del concepto de pendiente, en el sentido de su utilidad para resolver problemas matemáticos o del mundo real y bajo la doble mirada: modelación y aplicación. Para más información ver (Sánchez et al., 2021).
En la segunda etapa, se presentan las soluciones de los profesores a un panel de expertos en el campo de la matemática educativa, con la finalidad de que evaluaran el grado en que se manifiesta cada tipo de significado en los problemas resueltos y también de modo general para cada resolutor. Los instrumentos implementados fueron tres. En primer lugar, se utilizó un temario contentivo de cuatro problemas: E1, E2, E3 y E4, los cuales están relacionados con el concepto de pendiente, de forma implícita como se muestra en la (Fig 1).
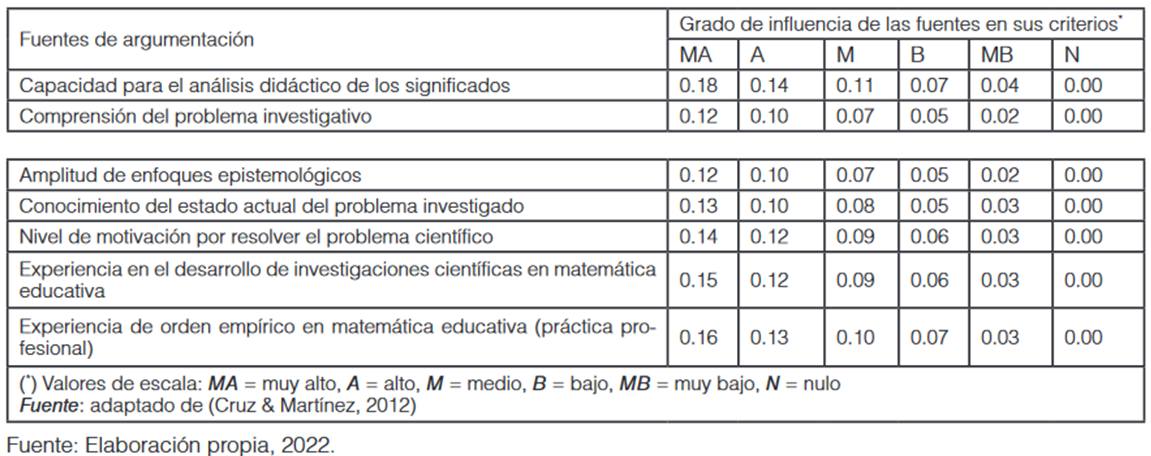
Como dispositivo de selección del panel de expertos, se solicitó el diligenciado de un cuestionario desarrollado por (Cruz & Martínez, 2012), el cual permite el cálculo de un índice de competencia experta k, resultante de la semisuma de sendos parámetros: un coeficiente de conocimientos acerca del tema investigado k c , y un coeficiente k a relacionado con el grado de incidencia de siete fuentes de argumentación, predefinidas bajo una escala tipo Likert. El valor de k c depende de forma directa de la autoevaluación del candidato, en una escala ordinal de 11 categorías: 0, 1,…, 10, donde el valor seleccionado se divide por 10. El valor nulo expresa ausencia total de conocimiento acerca del tema investigado, mientras que el valor 10 evidencia un conocimiento pleno. El cálculo de k a depende de la suma de pesos asignados para diferentes grados de influencia de cada fuente de argumentación, como se ilustra en la (Tabla 1).
En virtud de que 0 ( k c ( 1 y 0 ( k a ( 1, se obtiene que el coeficiente de competencia experta k = ½(k c + k a ) ( [0, 1], donde el punto de corte mínimo se fija en el valor k = 0.75 para la selección definitiva de los integrantes del panel.
El tercer instrumento consistió en una compilación digitalizada de todas las soluciones a los cuatro problemas descritos en la Figura 1. De cada profesor se presentaron sus cuatro soluciones, provistas respectivamente de rejillas formadas por cuatro casillas. En la rejilla, cada experto evaluó el grado de presencia de los cuatro tipos de significados, ya sea algebraico (Al), analítico (An), geométrico (Ge) o contextual (Co) sobre el concepto de pendiente. Para consignar los criterios se estableció la escala ordinal: 0, 1,…, 5, donde el valor nulo indica ausencia total del significado correspondiente y 5 expresa una presencia absoluta. Los valores no son excluyentes, de modo que en un mismo problema es posible identificar diferentes significados, con niveles independientes de manifestación. Además de la evaluación correspondiente a cada problema, también se solicitó el diligenciado de una rejilla adicional, a fin de que los expertos también emitieran una evaluación general del grado en que se expresan los significados en cada resolutor.
Participantes y variables.
En la primera etapa se seleccionó una muestra de 17 profesores de la Facultad de Matemática de la Universidad Autónoma de Guerrero (UAGro), todos con experiencia de al menos cinco años en la educación superior. Cada uno de los profesores fue invitado a participar en la solución del temario contentivo de los cuatro problemas. La comunicación fluyó de manera diáfana, con el compromiso expreso de que el uso de los resultados se mantendría bajo estricta confidencialidad. Los profesores contaron con tres días naturales para el diligenciado del instrumento, cuyas respuestas se recopilaron por la vía del correo electrónico o de forma directa. Todos recibieron una carta de agradecimiento por su amable colaboración.
Para la preselección del panel, en la segunda etapa, se exploraron tres redes sociales científicas: Academia, LinkedIn, y ResearchGate, a fin de conformar una preselección de 50 posibles expertos, por intermedio de la búsqueda automatizada de las palabras claves “matemática educativa” y “educación matemática”. La preselección priorizó el contexto latinoamericano, así como la representatividad de países del área. En la primera comunicación, los posibles expertos recibieron una carta de invitación para participar en el estudio, con una explicación sintética de los objetivos, del problema de investigación, así como un breve resumen de la tipología de significados del concepto de pendiente. También recibieron copia del cuestionario autoevaluativo, para el cálculo del índice de competencia experta, y la solicitud de su diligenciado en el término de una semana. De forma explícita se declaró el compromiso pleno de confidencialidad, ética y transparencia en el manejo de la información. En la segunda comunicación, se informó individual y gentilmente el resultado de la inclusión o no al panel participante. Seguidamente, cada miembro del panel recibió la compilación condensada del conjunto de soluciones, con sus rejillas evaluativas correspondientes. Los expertos seleccionados contaron con un mes de tiempo disponible para enviar, por vía del correo electrónico, los resultados de sus evaluaciones correspondientes.
El significado que los profesores tienen acerca del concepto de pendiente constituye la variable fundamental de la presente investigación. El análisis de dicha variable se sustenta en los significados fundamentales: analítico, algebraico, geométrico, y contextual. Por tanto, en un individuo puede manifestarse un significado marcadamente analítico, en el sentido de utilizar métodos propios del cálculo diferencial en la solución de problemas que tienen como centro el concepto de pendiente. Asimismo, un individuo puede mostrar un significado en un sentido general, en tal sentido la propia naturaleza del problema a resolver será la que favorecerá el despliegue de los diferentes tipos de significados.
Las variables independientes están comprendidas por los profesores y los expertos. Diferencias entre las formas de percibir y de realizar el significado, son aspectos de interés para la presente investigación. Por su parte, la variable dependiente (el significado del concepto de pendiente) será analizada con ayuda de los valores que aporta la rejilla evaluativa: en cada problema y en la valoración general.
Análisis de las evidencias empíricas.
El análisis de los datos se desarrolla a partir de la información que provee el criterio valorativo del panel de expertos. Cada rejilla aporta la evaluación del nivel en que se manifiesta el significado, conforme a la escala establecida en seis categorías (0-5), y para cada tipo de significado posible (An, Al, Ge y Co). Esta evaluación se realiza de manera local, centrada en cada problema (E1, E2, E3 y E4), y también de manera global, conforme a la valoración general de las cuatro respuestas de cada profesor (P01, P02,…, P17).
Seguidamente, se despliega un análisis descriptivo, basado en los valores medios de las evaluaciones. También se utilizan métodos de clasificación jerárquica para develar posibles conglomerados respecto a las variables nominales. En vista de que las rejillas describen evaluaciones particulares (relativas a cada problema) y generales (basadas en el conjunto de los cuatro problemas), también se exploran modelos de regresión lineal múltiple que describan relaciones objetivas subyacentes. Todo el análisis estadístico se implementa con ayuda del paquete SPSS (IBM Corp., 2020). El análisis de las evidencias empíricas culmina con el establecimiento de una tipología de problemas, inherentes al despliegue y predominio de significados en las soluciones al conjunto de problemas.
Resultados y discusión
Los 17 profesores seleccionados enviaron sus respuestas por los canales de comunicación establecidos. Cuatro de ellos requirieron de un tiempo adicional y el proceso de recopilación de información se extendió por una semana. Después de una revisión preliminar se observó que las respuestas del docente P14 fueron algo superficiales, mientras que los profesores P06, P11 y P15 dejaron problemas sin responder. Por este motivo, se eliminan sus ítems del presente estudio. Así, quedan definitivamente las soluciones de 13 profesores, las cuales conforman la compilación digitalizada provista de las rejillas evaluativas. A modo de ilustración, la (Figura 2) refleja las respuestas de los profesores P01, P05, P13 y P17 a los problemas E1, E2, E3 y E4, respectivamente. En el caso de la solución P17-E4, aparece en la parte inferior derecha un ejemplo de rejilla para su evaluación correspondiente.
Fuente: Tomada de la respuesta de los profesores.Fig. 2 - Ejemplos de respuestas dadas por los profesores a las preguntas formuladas.
En busca de economía del tiempo, de forma simultánea se envía la primera comunicación a los posibles expertos. Transcurrida una semana, se obtiene respuesta de 27 de ellos (54.0%). Inicialmente se excluyen dos, a causa de no presentar el formulario para la determinación del índice de competencia experta k. El cálculo de este coeficiente conlleva a conformar un panel definitivo de 21 expertos, pues en cuatro casos se obtuvieron valores excluyentes de k < 0.75. A continuación, se envía al panel la compilación digitalizada de respuestas, con sus rejillas evaluativas correspondientes.
Al cabo de un mes, se obtiene respuesta de 12 integrantes del panel. Se solicita amablemente la respuesta de los restantes expertos y transcurridas otras dos semanas, se logra recopilar las evaluaciones emitidas por 15 expertos. En dos casos fue necesario solicitar correcciones formales, a causa de un llenado inadecuado de las rejillas evaluativas. Los 15 expertos que respondieron poseen doctorados en el campo de la matemática educativa, son investigadores activos con un RG (ResearchGate Score) promedio de 8.3 y un índice de H (índice de Hirsch en Google Scholar) de 10.1. Los países de procedencia son México (5), Cuba (3), Colombia (2), Argentina (2), Estados Unidos (1) y España (2).
Análisis estadístico de las evidencias empíricas.
El diligenciado de las evaluaciones produce una matriz de 15(13 = 195 filas, correspondientes a los 15 expertos y los 13 profesores seleccionados, así como 22 columnas compuestas por dos variables nominales (Exp = expertos y Prof = profesores), y 20 variables ordinales (cada una de los cuatro tipos de significado, para los cuatro problemas y en la valoración general).
Tomando en consideración las evaluaciones desarrolladas por todo el panel de expertos, la (Tabla 2) ilustra el resultado descriptivo fundamental, para cada uno de los 13 profesores seleccionados.
Tabla 2 - Valores medios en las evaluaciones del panel de expertos.
| Prof. | E1 | E2 | E3 | E4 | General** | |||||||||||||||
| Al | An | Ge | Co | Al | An | Ge | Co | Al | An | Ge | Co | Al | An | Ge | Co | Al | An | Ge | Co | |
| P01 | 3.47 | 3.27 | 1.20* | 0.87 | 0.27 | 4.67 | 0.20 | 0.20 | 2.93 | 1.00 | 3.20 | 0.27 | 3.87 | 0.73 | 2.53 | 0.40 | 3.47 | 1.53 | 1.40 | 0.27 |
| P02 | 2.53 | 3.53* | 0.60 | 0.73 | 2.33 | 4.60 | 0.33 | 0.60 | 2.53 | 1.80 | 4.73 | 0.27 | 4.87 | 0.33 | 4.53 | 0.87 | 3.67 | 2.47 | 3.07 | 1.00 |
| P03 | 4.13 | 2.33 | 2.80 | 0.20 | 1.60 | 4.20 | 0.20 | 0.73 | 0.73 | 0.93* | 0.93* | 0.33 | 1.80* | 0.53 | 0.73 | 0.60 | 1.87* | 2.40 | 2.13* | 0.47 |
| P04 | 4.40 | 3.07 | 1.53 | 0.27 | 2.27 | 4.80 | 2.67 | 0.13 | 3.53 | 1.33 | 4.20 | 2.87 | 2.80 | 0.20 | 2.53 | 0.27 | 3.73 | 2.13 | 2.47 | 0.53 |
| P05 | 4.20 | 4.07 | 3.20 | 0.33 | 0.73 | 4.73 | 0.60* | 0.33 | 1.33 | 0.93 | 4.67 | 0.27 | 3.73 | 0.73 | 1.80 | 0.33 | 3.20 | 2.87 | 2.67 | 0.33 |
| P07 | 4.40 | 1.67 | 2.07* | 0.40 | 2.07 | 1.13* | 2.33 | 0.47 | 0.80 | 0.53 | 3.13 | 2.53 | 0.13 | 0.40 | 1.33 | 2.80 | 3.40 | 0.53 | 2.53 | 1.80 |
| P08 | 4.27 | 1.40 | 0.27 | 0.20 | 0.67 | 3.00* | 1.13 | 0.13 | 0.07 | 0.27 | 1.40 | 1.40 | 3.53 | 2.80* | 2.40 | 0.27 | 3.67 | 2.13 | 0.60 | 0.67 |
| P09 | 3.93 | 2.67 | 0.60 | 0.27 | 1.27* | 4.73 | 0.13 | 0.60 | 1.87 | 0.13 | 3.53 | 2.00 | 1.33 | 3.00 | 1.67* | 2.20 | 3.80 | 4.13 | 1.53 | 1.93 |
| P10 | 4.60 | 2.40 | 0.33 | 0.73 | 2.13 | 3.87 | 1.20 | 0.93 | 2.00 | 0.60 | 4.20 | 2.40 | 4.47 | 0.47 | 4.60 | 0.20 | 4.47 | 2.40 | 3.27 | 1.60 |
| P12 | 4.00 | 1.40 | 0.40 | 0.60 | 0.33 | 3.07 | 1.07 | 0.13 | 0.80 | 0.80 | 0.87 | 2.60 | 1.80 | 2.27 | 3.73 | 0.13 | 1.27 | 2.20 | 2.00 | 1.60 |
| P13 | 3.00* | 1.47 | 4.53 | 1.33 | 0.33 | 0.27 | 3.20 | 1.33 | 0.13 | 1.33 | 2.27 | 0.93 | 1.00 | 1.40* | 3.67 | 1.80 | 2.00 | 0.73 | 3.13 | 1.53 |
| P16 | 3.13 | 0.93* | 0.40 | 0.47 | 0.27 | 3.67 | 3.33 | 1.20 | 1.73 | 0.20 | 0.47 | 2.67 | 3.00 | 0.07 | 1.87 | 0.27 | 2.27 | 1.67 | 1.20 | 1.47 |
| P17 | 2.87 | 0.93* | 3.60 | 0.73 | 2.00 | 3.53 | 0.40 | 0.33 | 2.87 | 1.07 | 3.73 | 1.33 | 3.33 | 4.13 | 2.67 | 0.47 | 2.73 | 2.60 | 2.53 | 0.20 |
| Total | 3.76 | 2.24 | 1.66 | 0.55 | 1.25 | 3.56 | 1.29 | 0.55 | 1.66 | 0.75 | 2.77 | 1.47 | 2.74 | 1.31 | 2.62 | 0.82 | 3.04 | 2.14 | 2.19 | 1.03 |
(*) Valores medios con desviación típica mayor o igual que 1 (20% o más del rango de la escala).
(**) Se refiere a la evaluación de las respuestas en su conjunto (E1, E2, E3 y E4 a la vez).
La amplia mayoría de los valores medios experimenta una desviación típica inferior a la unidad. Este hecho aporta evidencia de que la percepción de los expertos fue bastante similar en referencia a cada profesor en el plano individual, para cada problema, y también en su evaluación general. Sin embargo, son visibles ciertas diferencias entre los profesores, tanto en problemas puntuales como en su proceder general ante el conjunto de los cuatro problemas.
Los valores sombreados corresponden a las respuestas ilustradas en la (Figura 1). En el caso de P01-E1, los expertos aprecian un predominio del significado algebraico (3.47) y del analítico (3.27), lo cual puede estar dado por la utilización del concepto de función lineal y el cálculo de la pendiente como razón entre diferencias. En el caso de P05-E2, se aprecia un predominio muy marcado del significado analítico (4.73), mediado por el empleo del concepto de derivada. En P13-E3 se observa una ligera manifestación del significado geométrico (2.27), probablemente motivado por la argumentación basada en el cálculo de razones entre las longitudes de catetos e hipotenusas, la rotación de figuras y el concepto de perpendicularidad. Finalmente, en P17-E4 predomina el significado analítico (4.13) y un poco menos el algebraico (3.33). Se trata de una solución basada en el cálculo de la pendiente como coeficiente en una ecuación lineal, aspecto que implicó la introducción de un sistema de coordenadas cartesianas.
En la última fila, referida a los promedios generales, se aprecia el predominio del significado algebraico en los problemas E1 y E4 (3.76 y 2.74, respectivamente). En el problema E2 predomina el significado analítico (3.56), motivado por la estrecha conexión entre el concepto físico de velocidad instantánea y el concepto de derivada, así como la utilidad que reviste el teorema de Rolle. Por su parte, en el problema E3 predomina el significado geométrico (2.77), lo cual también se expresa en un segundo nivel jerárquico para el problema E4 (2.62). A diferencia de los dos primeros problemas, el propio enunciado de estos problemas pone por delante un objeto geométrico, lo cual puede condicionar el tipo de solución. No obstante, como pudo verse en la solución de P17-E4, este supuesto condicionamiento no es determinante (Figura 1). Las columnas correspondientes a la percepción general revelan que, a excepción de los profesores P03, P12 y P16, en el resto de los casos predomina el significado algebraico. En los promedios correspondientes a la valoración general, para el total de profesores, se reafirma el predominio del significado algebraico: Al = 3.04 > Ge = 2.19 > An = 2.14 > Co = 1.03.
Llama la atención el hecho de que el significado de tipo contextual ocupa los valores más bajos, tanto en las respuestas a cada problema, como en sentido general. Sin embargo, en algunos casos los profesores utilizaron el concepto de pendiente no como un elemento a calcular en primera instancia, sino como una herramienta argumentativa para la solución del problema. Un ejemplo puede verse en la solución del profesor P04 al tercer problema, relacionado con la supuesta paradoja en el corte de una alfombra rectangular. La (Tabla 2) refleja que los expertos evalúan P04-E3 con los valores medios Al = 3.53, An = 1.33, Ge = 4.20, y Co = 2.87. Este último valor es, precisamente, el máximo alcanzado para el significado de tipo contextual, en todo el universo de respuestas.
La (Figura 3) muestra la solución de P04-E3. Si bien predomina el cálculo de la pendiente como coeficiente de una ecuación lineal (significado predominantemente algebraico), el resolutor se apoya en la no colinealidad entre los puntos A, F y G. Con la finalidad de sostener su criterio, el profesor expresa que: “… para probar esta última afirmación haremos uso de la pendiente…”. Por tanto, el resolutor pone por delante el concepto de pendiente, como noción matemática que sirve de argumento esencial. En fin, el cálculo del valor de la pendiente constituye una realización de cierto proceso de modelación matemática. Ello justifica que los expertos hayan ponderado el significado contextual en sus respectivas evaluaciones.
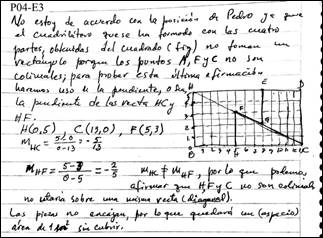Fuente: Tomada de la respuesta de los profesores.Fig. 3 - Argumentos de naturaleza contextual en el significado del concepto de pendiente.
Para el análisis de datos multivariados se toma en consideración el conjunto de expertos, las variables dependientes para los 13 profesores producen un dendograma en forma de árbol de dos ramas. Una de las ramas está formada por un único individuo, con un nivel de desemejanza inferior al 15%. El bajo nivel de disimilitud permite afirmar que la amplia mayoría de los expertos tuvo una percepción similar en el universo de evaluaciones. Particularmente, el análisis puntual del experto con percepción relativamente atípica, revela que adoptó una postura más severa en sus evaluaciones ante situaciones con limitada argumentación. Por otro lado, el análisis de las variables dependientes centradas en cada problema particular (se excluye la evaluación general) aporta un hecho interesante relacionado con su clasificación jerárquica.
El dendograma de la (Fig 4) refleja la existencia de un árbol formado por dos conglomerados, con una desemejanza cercana al 25% (método de agrupación basado en enlaces entre grupos y medida basada en el cuadrado de la distancia euclidiana).
Puede observarse un grupo compuesto por 9 variables y otro por 7, de las 16 examinadas (16 = 4 problemas ( 4 tipos de significado). Independientemente de las diferencias obvias que subyacen entre los cuatro problemas, relacionadas con su formulación, los objetos matemáticos que involucran, el nivel de complejidad, entre otros aspectos matemáticos, existe un elemento que llama la atención. En efecto, una mirada centrada en el tipo de significado revela cierto desbalance respecto al significado geométrico. Si bien los tipos restantes de significado están distribuidos de un modo más uniforme, el significado geométrico es ampliamente dominante en el clúster superior de la Figura 4, incluso en dos subgrupos de mayor jerarquía. No ocurre así en el clúster inferior, donde predomina lo algebraico y analítico. Por tanto, las evidencias sugieren una especie de dicotomía en la forma de clasificar los significados: una centrada en lo geométrico, y otra centrada en lo algebraico y lo analítico, fundamentalmente. El significado contextual se observa con una distribución más balanceada en ambos conglomerados del dendograma, incluso con niveles de disimilitud inferiores al 10%.
La evaluación general del grado en que se manifiesta cada tipo de significado, en mayor o menor medida está relacionada con las evaluaciones específicas que el experto realizó en los respectivos problemas. Si se consideran como observaciones las 15(13 = 195 evaluaciones realizadas por los 15 expertos a los 13 profesores, entonces es posible explorar ciertas regresiones lineales múltiples. Esta idea se concreta al determinar en qué medida la variable dependiente Gen Sig depende del conjunto de variables independientes Ei Sig , donde Gen = evaluación general, Ei = problema i, y el subíndice Sig ({Al, An, Ge, Co} indica el tipo de significado. El procesamiento estadístico realizado se resume en la (Tabla 3).
Tabla 3 - Resultados del análisis de regresión lineal múltiple.
| Variable dependiente | Varianza explicada | Constante |
|
|
|
|
||||||
|
|
( | (1 | (2 | (3 | (4 | |||||||
|
|
0.07 | 3.65** | 1.90 | 4.44** | -0.20 | -2.19* | -0.06 | -0.74 | 0.09 | 1.20 | 0.21 | 2.19* |
|
|
0.38 | 29.04** | 2.69 | 12.31** | 0.29 | 3.62** | 0.09 | 0.96 | 0.24 | 3.46** | -0.68 | -7.26** |
|
|
0.06 | 2.99* | 2.19 | 6.31** | -0.13 | -2.18* | 0.26 | 1.82 | 0.04 | 0.67 | 0.15 | 1.71 |
|
|
0.23 | 14.12** | 1.43 | 9.97** | -0.03 | -0.35 | -0.22 | -3.31** | -0.18 | -5.07** | 0.12 | 2.56* |
(*) p < 0.05, (**) p < 0.01
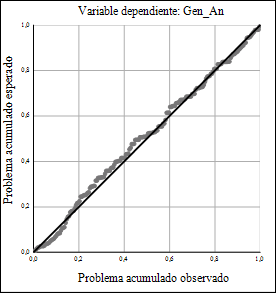
Los coeficientes de determinación R 2 son relativamente bajos. En particular, el análisis de regresión tiene mejor bondad de ajuste para la evaluación general del significado analítico (Gen An ), con una proporción del 37.9% de la varianza total explicada. La prueba ANOVA correspondiente produce un estadístico F = 29.04, altamente significativo (p < 0.01, gl = 4). Además, cuatro de los cinco coeficientes lineales se calculan con niveles de significación aceptables para el estadígrafo t, donde el cálculo adicional del factor de inflación de la varianza produce valores VIF < 2; o sea, se satisface el requisito de no multicolinealidad. En general, para todas las variables dependientes no se observan residuos con relaciones problemáticas respecto a las variables predictoras. Por ejemplo, retomando la variable Gen An , el gráfico P-P de la (Fig 5) muestra que los residuos se distribuyen aproximadamente de manera normal.
Con base en estas consideraciones, las evidencias sugieren que las relaciones entre las evaluaciones generales y las particulares, subsisten bajo un modelo de regresión lineal. De los cuatro casos, el modelo más adecuado corresponde al significado analítico: Gen An = 2.69 + 0.29(E1 An + 0.09(E2 An + 0.24(E3 An - 0.68(E4 An . Por ejemplo, en la Tabla 2 puede apreciarse que el profesor P09 obtuvo mayor evaluación promedio en el significado analítico (An = 4.13). Para este tipo de significado, el primer experto evaluó los problemas resueltos por P09 con los valores E1 An = 5, E2 An = 1, E3 An = 3, E4 An = 3, y el conjunto de los cuatro problemas con Gen An = 3. Puede verse que esta evaluación se describe adecuadamente por el modelo anterior: Gen An = 2.69 + 0.29(5 + 0.09(1 + 0.24(3 - 0.68(3 = 2.91.
El cuestionario utilizado en esta investigación ha sido concebido para explorar el grado en que se manifiestan los significados analítico, algebraico, geométrico y contextual de la pendiente en profesores universitarios de Matemática. El problema E1 exige la modelación de una situación asociada, en lo fundamental, a significados geométricos y algebraicos de la pendiente. Por lo tanto, se espera que para su solución los profesores recurran a significados tales como: la razón entre el cateto vertical y el cateto horizontal del triángulo rectángulo, cuya hipotenusa yace sobre la recta; el desplazamiento vertical por cada unidad de desplazamiento horizontal; y la razón entre la diferencia de las ordenadas y la diferencia de las abscisas de dos puntos que pertenecen a la recta, esto es, una razón de la forma de la (Ecuación 2), con (Ecuación 1)con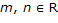 
.
Las respuestas a los Incisos (b)-(e) evidencian algunos de los significados que poseen los profesores sobre el concepto de pendiente al establecer las relaciones necesarias entre dicho concepto y los conceptos que definen las exigencias del problema. Por ejemplo, la rapidez de llenado en un intervalo de tiempo dado, el tramo en el que la altura del agua experimenta mayor variación, entre otras ideas. Además, las soluciones ponen de manifiesto el uso de representaciones geométricas, algebraicas y contextuales, asociadas con la pendiente. La (Fig 6) ilustra la respuesta dada por el profesor P17 al Inciso (d).
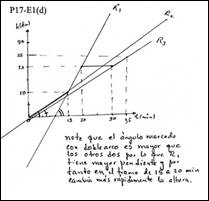Fuente: Tomada de la respuesta de los profesores.Fig. 6 - Una respuesta con significado predominantemente geométrico.
El resolutor despliega un razonamiento predominantemente geométrico sobre la base del ángulo de inclinación. De aquí concluye que como el ángulo es mayor, entonces la recta en cuestión tendrá mayor pendiente. Con ello, dicho profesor está asociando la idea de que: a mayor ángulo de inclinación, mayor pendiente. Esto último no es cierto en general. Un significado para la pendiente, de esta naturaleza, contribuiría a formar un conocimiento limitado, que fuera de este contexto no es cierto. Además, por otro lado, no se analiza ni se precisan las condiciones bajo las cuales se cumple dicha relación.
Otra situación que se presenta en el problema E1 está dada en el significado asignado a la pregunta: … ¿Durante qué tiempo? El 56.3% de los profesores respondió a dicha pregunta, proponiendo un intervalo en lugar de una cantidad minutos. Esta forma de responder da cuenta del significado que se despliega para comprender la situación. Incluso, también se manifiesta cierta inconsistencia en el uso de variables, por ejemplo, al definir la función que modela el proceso como se muestra en la (Fig 7), donde la función que depende de la variable x viene dada en términos de t.
Fuente: Tomada de la respuesta de los profesores.Fig. 7 - Una inconsistencia observada en el empleo de las variables.
El problema E2 tiene como objetivo estimular que emerjan significados analíticos tales como la derivada de la función en un punto, la pendiente de la recta secante y la pendiente de la tangente en un punto. También significados de naturaleza contextual con base en las relaciones conceptuales de velocidad instantánea y tasa de cambio de la función del desplazamiento en un punto. Las respuestas producidas por los profesores al problema planteado se centran en dos direcciones principales: La primera relacionada con significados predominantemente analíticos del concepto de pendiente. Es notorio que el 62.7% de los profesores utiliza en sus respuestas propiedades básicas de las funciones, sin mostrar evidencia de algún tipo de representación geométrica y utilizando, básicamente, los teoremas de Rolle y del valor medio del cálculo diferencial. De este modo garantizan la existencia de un punto en el que la tasa de cambio instantánea coincide con la tasa de cambio media de la función en un intervalo dado. La segunda está dada en la combinación de los significados analíticos y geométricos, la cual fue seguida por el 29.4% de los profesores que participaron en el estudio. Durante el proceso de análisis y resolución, estos recurrieron al significado geométrico de la derivada, con lo cual establecieron conexión entre la pendiente de la secante y la tangente, auxiliados del teorema del valor medio.
La (Fig 8) ilustra ambos despliegues del significado predominantemente analítico (izquierda) y mixto analítico-geométrico (derecha).
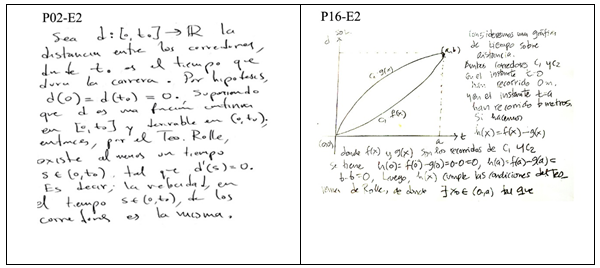Fuente: Tomada de la respuesta de los profesores.Fig. 8 - Predominio de diferentes significados en la solución de un problema.
Otro aspecto a destacar en las respuestas de los profesores al problema E2, está dado en la confusión que se presenta entre el cambio de una magnitud en un instante y la tasa de cambio instantáneo de dicha magnitud. Es decir, matemáticamente se manifiesta confusión entre el valor de la variación de la función y la tasa de cambio de dicha función en un punto. Por ejemplo, el profesor P09 sugiere que: “… al trazar las gráficas de distancia contra el tiempo de los corredores, estas van del punto
hasta
, por continuidad debe haber un punto de intersección y es justo cuando tienen la misma velocidad” (sic). Una situación similar se ha reportado en las investigaciones desarrolladas por (Janvier, 1978; McDermott et al., 1987; Stump, 2001), aspecto que denominan “confusión pendiente/altura”.
El problema E3 pretende explorar, en lo fundamental, significados geométrico y contextual sobre la pendiente que poseen los profesores al darles la posibilidad de decidir si se puede o no formar un rectángulo con las piezas dadas. Básicamente, el problema se reduce a probar la alineación o no de tres puntos que supuestamente estarían en la diagonal de dicho rectángulo. Para dar respuesta al problema planteado, los profesores proponen dos variantes: probar la no alineación de los puntos utilizando la pendiente, como se puede ver en la Figura 2, respuesta P13-E3, y en la Figura 3, respuesta de P04-E3. Este último caso utiliza el supuesto de que la pendiente es constante, por lo que si se tienen tres puntos y se toman dos a dos y resulta que las pendientes formadas por cada pareja coinciden, se tiene la colinealidad. Esta variante fue seguida por el 64.7% de los profesores.
La estrategia usada por P03, para establecer la no alineación de los puntos, prueba que los triángulos rectángulos AIF, FHC y ABC no son semejantes. Para ello emplea la razón “…cateto vertical entre el cateto horizontal” (Figura 9) como base para calcular la pendiente de una línea recta y verificar que estas razones no coinciden, lo cual significa que los tres puntos no son colineales. Al razonar por semejanza, con base en los catetos de triángulos rectángulos, subyace el significado geométrico de pendiente. Esta vía fue utilizada por el 23.5% de los profesores.
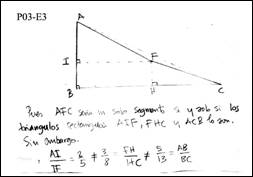Fuente: Tomada de la respuesta de los profesores.Fig. 9 - Significado geométrico basado en el concepto de semejanza.
El problema E4 explora la capacidad para emplear el significado de pendiente en una situación de geometría sintética donde no existen indicios declarados como rectas, ecuaciones de rectas, sistemas de coordenadas, entre otros conceptos. También estimula la búsqueda de otras vías de solución, así como el establecimiento de relaciones conceptuales entre las diferentes ideas. Como resultado, el 70.6% de los profesores desarrollaron en esencia uno de los siguientes procederes: la implementación de recursos de geometría analítica junto al despliegue directo y explícito del concepto de pendiente, el cual relacionan con significados geométricos o algebraicos; y el empleo de semejanzas de triángulos para luego señalar su relación con el concepto de pendiente, donde la noción de proporcionalidad es una especie de idea conectora. Esta última variante se manifiesta en el caso ilustrado en la (Figura 10).
Fuente: Tomada de la respuesta de los profesores.Fig. 10 - Relaciones entre significados desplegados en distintas soluciones.
Cabe señalar que tres profesores desarrollaron soluciones en las que combinan la semejanza de triángulos y elementos de trigonometría. Aunque utilizan la tangente del ángulo no llegan a relacionarla con la pendiente de una recta. Es importante destacar el papel que juegan los significados que despliega el profesor para comprender el problema y posteriormente elabrorar un plan o estrategia de solución. Precisamente, estos significados facilitan la contextualización del proceso resolutivo. Así un problema puede emerger dentro de un contexto, pero no necesariamente tiene que resolverse con las herramientas de dicho contexto.
Conclusiones
El objetivo del presente estudio consistió en identificar y valorar los significados matemático-cognitivos que poseen los profesores universitarios sobre el concepto de pendiente. En esta dirección se identificaron cuatro tipos de significados: analítico, algebraico, geométrico y contextual, a partir de las respuestas dadas por los profesores a los problemas planteados. El significado geométrico tuvo mayor presencia que los demás significados, en lo fundamental, mediante representaciones como: la razón geométrica, la tangente del ángulo de inclinación, razón entre las longitudes de los catetos de un triángulo rectángulo formado por la recta, el eje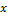 
y la paralela al eje 
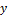. El significado algebraico se evidenció a través de diferentes representaciones relacionadas con el concepto de razón de cambio. En esencia, el énfasis se pone en el cálculo el valor de 
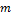en la (Ecuación 1), o bien en calcular una razón del tipo (Ecuación 2). Mientras que el significado analítico se manifestó principalmente a través del concepto de derivada de una función en un punto, su interpretación geométrica y como la razón de cambio instantánea para una función.
Los procederes desplegados por los profesores en las soluciones, revelan una tendencia a tratar de visualizar sus ideas recurriendo a representaciones geométricas clarificadores, hecho que corrobora lo reportado por (Zaslavsky et al., 2002; Hoffman, 2015). También, se observaron ciertas relaciones que establecen los profesores entre diferentes significados del concepto analizado, esencialmente entre los significados geométrico y algebraico, así como los significados geométrico y analítico coincidiendo con los hallazgos presentados por (Byerley & Thompson, 2017). Los procedimientos de soluciones desarrollados reflejan también que los profesores emplean el concepto de pendiente como una herramienta argumentativa y de comprensión para la solución de problemas.
De las soluciones aportadas por los profesores se identificaron algunas situaciones, tales como la ausencia de rigor al representar la idea de solución, o bien en el marco de la argumentación. Términos y frases tales como “la pendiente de la función”, “a mayor ángulo de inclinación mayor pendiente” y “la pendiente es la derivada de la función en los puntos donde existe” (sic) abusan del rigor y podrían provocar distorsiones en la idea que se quiere transmitir. También se manifestó confusión entre el cambio de una magnitud en un instante y la tasa de cambio instantáneo de dicha magnitud.
A partir de las evidencias empíricas se puede inferir que los expertos perciben el significado del concepto de pendiente con un alto grado de similitud y uniformidad. Dichos expertos identifican el significado del concepto de dos formas fundamentales: una centrada en lo geométrico y otra centrada en lo algebraico-analítico. El significado contextual evidenció la percepción más baja de todos los tipos de significados del concepto investigado. Ello estuvo motivado, en lo fundamental, porque las respuestas y soluciones dadas por los profesores a los problemas planteados, se centraron en los aspectos matemáticos teórico-formales; descuidando en sus argumentaciones y justificaciones los elementos contextuales, lo que provocó que este significado no se revelara en toda su extensión.
A la luz de los resultados obtenidos, se concluye que es necesario prestar mayor atención a la formación y desarrollo del concepto de pendiente, en el proceso inicial y permanente de formación del profesional de la educación matemática. Es necesario que este concepto no quede anclado en un plano estático, ya sea geométrico, analítico, algebraico, o contextual, sino interrelacionado dialécticamente en una pluralidad de planos. De este modo, el concepto de pendiente será transmitido y aprehendido de modo profundo y riguroso.
