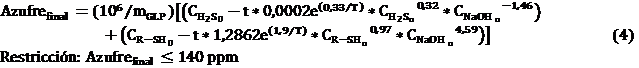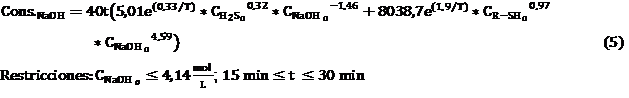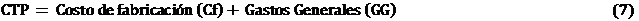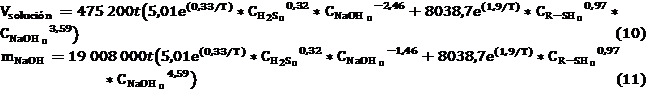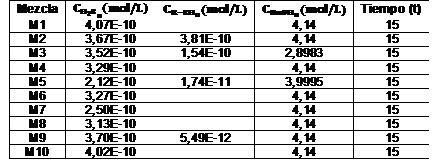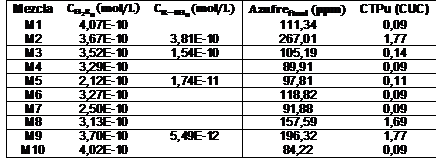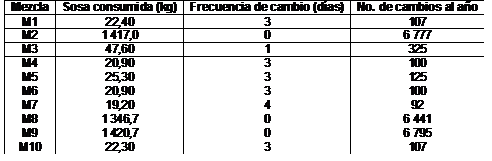Introducción
El análisis de procesos, como vía para lograr la intensificación de los procesos tecnológicos de la industria química consiste en un amplio análisis científico-técnico y técnico-económico de un proceso existente o concebido, en lo referente a las posibilidades de realización óptima de los objetivos previstos, por ello constituye un elemento importante para tomar decisiones más científicas y responsables.
El análisis de procesos sirve para descubrir las partes débiles en el proceso de producción correspondiente y para la creación de medidas para su eliminación parcial o completa lo que conduce a un aumento de su efectividad, permitiendo de esta forma un mejor aprovechamiento de las materias primas, la energía y los medios de trabajo, así como un aumento de los grados de eficiencia de la fuerza de trabajo y el mejoramiento de las condiciones materiales bajo las cuales ellos laboran. La intensificación de la producción mediante el análisis complejo de procesos, requiere la elaboración de objetivos económicos en cada industria de forma concreta, entre lo que se encuentra de acuerdo con la experiencia acumulada: 1
- Aumento de la calidad y la cantidad de los productos elaborados.
- Disminución de los consumos específicos y absolutos de materiales y energía.
- Mejoramiento de las condiciones de trabajo.
- Ahorro de fuerza de trabajo.
- Disminución de la contaminación ambiental.
La función clave de la intensificación de procesos es su optimización, pero como se conoce, la optimización de procesos se hace con apoyo de modelos matemáticos de los procesos elaborados de los valores reales del comportamiento de los propios procesos2 por lo que es adecuado conceptualizar sobre la modelación de proceso. Un modelo es una construcción mental o material que crea el investigador a partir de su conocimiento práctico y teórico del objeto de investigación y le sirve de guía y soporte para abordar el estudio de dicho objeto y su fenomenología.
Existen múltiples ventajas en el uso de modelos como herramientas poderosas para la toma de decisiones. Las principales son:
Consideración de aspectos fundamentales del sistema que serían muy difíciles o imposibles de analizar sin la ayuda de los modelos.
Definición precisa de los objetivos, estructura y restricciones del sistema.
Definición de parámetros, costos e indicadores de eficiencia que recogen los aspectos más relevantes para el análisis del sistema bajo estudio.
Evaluación sistemática de alternativas.
Rápida respuesta de análisis de sensibilidad, los cuales de otra forma serían demasiado dificultosos o imposibles.
Por el contrario, existen también algunas desventajas que deben ser evaluadas antes de emprender la tarea de formulación de un modelo para la solución de un problema. Ellas son:
Requerimiento y recolección de conjuntos de datos muy extensos y, en general, con altas exigencias en su grado de precisión.
Requerimiento de conocimientos altamente especializados para su formulación, solución y análisis de resultados.
Necesidad de disponer de sistemas de computación y programas complejos y costosos.
Requerimiento de tiempos de solución muy largos, los cuales, en algunos casos, pueden resultar prohibitivos.
A pesar de estas desventajas potenciales, cuando se emprende la tarea de modelar una situación real y se identifican los aspectos básicos a ser involucrados en el modelo con la información requerida necesaria, las ventajas potenciales superan ampliamente cualquier dificultad que se encuentre.3
Por otro lado, la optimización es encontrar una alternativa de decisión con la propiedad de ser mejor que cualquier otra en algún sentido. Esta tiene tres componentes fundamentales:
Función objetivo: medida cuantitativa del funcionamiento (de la bondad) de un sistema que se desea maximizar o minimizar.
Variable: decisiones que afectan el valor de la función objetivo que pueden ser independientes o dependientes.
Restricciones: conjunto de relaciones que las variables están obligadas a satisfacer.
Su resolución no es más que encontrar el valor que deben tomar las variables para hacer óptima la función objetivo satisfaciendo el conjunto de restricciones.4
La complejidad de las sociedades modernas y el progreso científico mundial han dado lugar al desarrollo y evolución de herramientas que contribuyan con el quehacer diario. El diseño, la implementación y la construcción de dichos instrumentos involucra elementos que envuelven la solución de problemas, basados en sistemas o modelos complejos y multifactoriales.
Esto ha llevado a la implementación de técnicas que optimizan la producción y eficiencia de las herramientas, como lo son los algoritmos creados para la simulación de circuitos y ejecución de cadenas completas de procesamiento de señales, los cuales evidencian la optimización de funciones objetivo con un número considerable de parámetros.5
En la búsqueda de estrategias que soporten la optimización simultánea de más de un criterio de costo o aptitud surge la optimización multiobjetivo.(6)Esta optimiza objetivos de manera conjunta, poniéndolos a competir entre sí, de modo que para cada valor de una función de aptitud o costo se obtiene lo mejor de los otros objetivos. Así, la solución del problema general es una combinación de las soluciones óptimas de cada objetivo, por lo que dicha solución no es única.6,7
En particular, la comunidad científica que trabaja en la implementación de algoritmos para la resolución de problemas de optimización multiobjetivo se divide en dos categorías, definidas por el tipo de funciones objetivo utilizadas. El primer grupo supone funciones objetivo de bajo costo computacional, se preocupa por la eficiencia global de los algoritmos de optimización en sí. Por otro lado, el segundo grupo asume un alto costo computacional de las funciones objetivo, por lo que se interesa por un proceso de optimización que reduzca el número de evaluaciones de dicha función, pues esta última domina la duración total de la optimización. 8
Este trabajo tiene como objetivo aplicar los métodos de solución de la optimización multiobjetivo para disminuir el consumo de sosa cáustica en la etapa de tratamiento de la nafta inestable en el proceso de obtención del gas licuado del petróleo (GLP).
Materiales y métodos
Las características del proceso estudiado requieren un enfoque de optimización considerando varios objetivos, por lo que su intensificación se debe considerar como una optimización multiobjetivo. Los principales métodos para resolver problemas de optimización multiobjetivo se clasifican en:
Métodos sin preferencias
El problema es resuelto mediante un método relativamente simple y solo se satisface con una solución óptima. Entre ellos se encuentran: método del criterio global o CompromiseProgramming, método del paquete proximal multiobjetivo,9) modelos gaussianos estocásticos. 10,11
Métodos heurísticos
Las heurísticas o métodos heurísticos son algoritmos construidos de manera intuitiva. Algunos autores denominan metaheurística a aquellos casos en los que el algoritmo de optimización utiliza a su vez subprocesos heurísticos, pero esta es una distinción no generalizada.12Entre las heurísticas más populares están Colonia de Hormigas (AC por sus siglas en inglés), Recocido Simulado (SA por sus siglas en inglés), Búsqueda Tabú (TS por sus siglas en inglés), Enjambre de Partículas (PS por sus siglas en inglés) y los algoritmos evolutivos (EA por sus siglas en inglés). Los EA se inspiran en conceptos de la evolución biológica tales como la reproducción, mutación, recombinación y selección;13 además, balancean la exploración y explotación del espacio de búsqueda de manera exhaustiva con pocas evaluaciones. En contraste, AC, SA y TS son los métodos más antiguos y tienden a realizar más llamadas a la función evaluadora.14
Métodos a priori
En este caso, la persona que toma las decisiones debe especificar su o sus preferencias, esperanzas y opiniones antes de comenzar el proceso de solución. Sin embargo, no siempre se sabe de antemano lo que es posible alcanzar en el problema y el grado de realismo de las expectativas.15Entre los métodos más conocidos se encuentran: método de la función del valor, método de ordenamiento lexicográfico y método de programación por metas.9
Métodos a posteriori
Los métodos a posteriori, también son llamados métodos para generar soluciones óptimas de Pareto. Miettinen9plantea que una vez que la frontera de Pareto (o parte de ella) es generada, ésta se expone al tomador de decisiones, quien selecciona la solución más preferida. El principal inconveniente es que el proceso de generación es usualmente costoso desde el punto de vista computacional. Algunos de los métodos más usados son: el método de las ponderaciones 15) y el método de ((-constraint. 16
Métodos interactivos
En los métodos interactivos, el tomador de decisiones trabaja en conjunto con un analista o un programa informático interactivo. Se puede decir que el analista trata de determinar la estructura de preferencias de la toma de decisiones de una manera interactiva, formando un patrón de solución y se repite varias veces. Después de cada iteración, se entrega información al tomador de decisiones y se le pide que responda a algunas preguntas o que dé algún otro tipo de información para que el modelo sea más representativo de la realidad. Algunos de los métodos utilizados son: método Interactivo del Sustituto Digno Trade-Off (ISWT por sus siglas en inglés), método de Geoffrion-Dyer-Freinberg (GDF), técnica de Optimización de Representación Secuencial (SPOT por sus siglas en inglés) y método de Tchebycheff, entre otros.15
Definición de las funciones objetivos
En el proceso objeto de estudio, las variables a optimizar son: la reducción de azufres totales en la corriente de entrada a la etapa de fraccionamiento, el consumo de sosa cáustica y los costos operacionales. Se ha definido que el orden de prioridad de estas variables es:
Azufre total en el GLP. Como éste es un parámetro de calidad medido para su comercialización, los cambios que se hagan en el proceso no pueden afectar negativamente este aspecto por lo que es considerado como el principal objetivo a cumplir.
Consumo de sosa. La sosa cáustica, como se ha mencionado anteriormente, es la solución que se utiliza para neutralizar los compuestos sulfurosos presentes en la nafta inestable, sin embargo, es un producto costoso y que genera grandes cantidades de agua sulfurosas alcalinas las cuales no son tratadas correctamente en la actualidad por lo que es necesario disminuir su consumo.
El costo total de producción unitario (CTPu). Todo proceso industrial lleva consigo un costo de operación, éste está constituido por, entre otras cosas, el consumo de materiales e insumos y en este caso, los materiales e insumos en los que se puede influir son el agua utilizada en la preparación de la solución alcalina y la sosa cáustica.
Definido el orden de prioridad o jerarquía se procede a obtener las funciones objetivos y sus restricciones.
Reducción de azufres totales
La cantidad de azufre presente en el producto final (Azufrefinal) de la unidad de fraccionamiento de gases es un parámetro que está regulado por los estándares de calidad: para el GLP regular hasta 140 ppm de azufres totales y para el GLP despentanizado hasta 5 ppm debido al alto poder corrosivo del azufre. En consecuencia, se hace necesario eliminar la mayor cantidad de compuestos sulfurosos en la etapa de neutralización. La función definida para la reducción de azufres totales,partiendo de la expresión cinética de las reacciones que tienen lugar en este proceso,es la siguiente:
donde
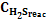 y
y 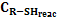 son las concentraciones de H2S y R-SH que reaccionan con la sosa cáustica, T la temperatura de reacción y tes el tiempo de reacción. Sustituyendo las ecuaciones 2 y 3 en la 1 se obtiene la siguiente función:
son las concentraciones de H2S y R-SH que reaccionan con la sosa cáustica, T la temperatura de reacción y tes el tiempo de reacción. Sustituyendo las ecuaciones 2 y 3 en la 1 se obtiene la siguiente función:
Por consiguiente, esta función se convierte en una restricción del sistema siendo la principal meta de este estudio.
Consumo de sosa cáustica
El tratamiento cáustico simple es un proceso de extracción (desulfuración), donde compuestos de azufre y fenoles son retirados de la nafta y se quedan en la sosa cáustica, disminuyendo su concentración, siendo posteriormente necesario su cambio. Debido a esto es necesario conocer la concentración óptima de sosa que permita una correcta desulfuración y que a su vez disminuya la frecuencia de cambio.
Según la literatura, 17 los volúmenes de los tambores se dimensionan frecuentemente para proporcionar un tiempo de espera de 30 min a 1 h (ver tabla 1). Para hidrocarburos de baja viscosidad como el propano y el butano, 5 a 10 min son más que suficientes.
Por tanto, la función objetivo definida para el consumo de sosa cáustica es la siguiente:
Costo total de producción
Para determinar los costos operacionales es factible el procedimiento recomendado por algunos autores. 18,19 Según los datos disponibles en la empresa, no fue necesario estimar todos los componentes de la metodología utilizada y se llegó a una estimación directa del capital fijo invertido de 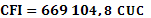 y del capital total invertido de
y del capital total invertido de 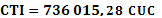 (1 CUC = 1 USD). Igualmente, para estimar un modelo de los costos total de producción (CTP) se procede a utilizar la tabla 27 de la literatura (19 que es como se representa en la tabla 2, en la cual algunos valores pueden ser determinados directamente de los controles del proceso tecnológico y otros estimados por varias vías. Siendo el precio de:agua: 1,55 CUC/m3(20y sosa cáustica: 0,7956 CUC/kg.21
(1 CUC = 1 USD). Igualmente, para estimar un modelo de los costos total de producción (CTP) se procede a utilizar la tabla 27 de la literatura (19 que es como se representa en la tabla 2, en la cual algunos valores pueden ser determinados directamente de los controles del proceso tecnológico y otros estimados por varias vías. Siendo el precio de:agua: 1,55 CUC/m3(20y sosa cáustica: 0,7956 CUC/kg.21
Según Peters y Timmerhaus (1991) el costo de fabricación (Cf) se determina como sigue:
Según algunos autores (1991),19 el costo total de producción se determina por la ecuación 7
Para el cálculo de los gastos generales (GG) se tuvo en cuenta solo con los gastos administrativos pues en el caso de estudio no tienen incidencia los aspectos restantes:
Sustituyendo las ecuaciones 6 y 8 en la 7 se obtiene un costo anual de:
Por definición el costo de producción unitario (CTPU) es el costo de producción anual entre el volumen de producción y el valor de la producción anual dependerá de variables que deciden el proceso y su productividad como son: el tiempo de reacción y concentración, lo que nos permite obtener una expresión de la forma siguiente:
Siendo el volumen de producción anual:
Siendo VT-401el volumen de la torre de fraccionamiento
Sustituyendo las ecuaciones 9 - 11 y 13 en la 12 se obtiene que:
Para realizar la optimización se utilizó el software MATLAB® pues este contiene un conjunto de herramientas que te permiten optimizar todo tipo de ecuaciones. Se utilizó la función fmincon pues las funciones objetivos determinadas anteriormente son funciones no lineales y el sistema tiene restricciones de igualdad y desigualdad. Para esto se introdujo en el software MATLAB® el código de programación que aparece en la figura1 para determinar los puntos óptimos en cada mezcla estudiada.
Esta función (fmincon) utiliza el método numérico cuasi-Newton. Los métodos cuasi-Newton, o métodos de métrica variable, buscan estimar el camino directo hacia el óptimo en forma similar al método de Newton. Estos métodos se llaman de cuasi-Newton porque no usan el hessiano verdadero, sino más bien una aproximación. Así, se tienen dos aproximaciones simultáneas: 1) la aproximación original de la serie de Taylor y 2) la aproximación del hessiano. Hay dos métodos principales de este tipo: los algoritmos de Davidon-Fletcher-Powell (DFP) y de Broyden-Fletcher-Goldfarb-Shanno (BFGS). Estos son similares excepto en detalles concernientes a cómo manejan los errores de redondeo y su convergencia. BFGS es, por lo general, reconocido como superior en la mayoría de los casos.22(
Discusión de los resultados
Definidas las funciones objetivos con sus restricciones se aplicó el método de optimización definido anteriormente. En la tabla 3 se muestran los resultados obtenidos en la optimización para cada mezcla estudiada.
Los resultados de la evaluación de los puntos óptimos en las ecuaciones 4 y 14 se muestran en la tabla 4 que sigue a continuación:
Como se puede observar en la tabla 4 la mayoría de las mezclas analizadas cumplen con la principal meta, y por tanto restricción, que es el contenido de azufre en el GLP regular por debajo de 140 ppm. También se observa que, aunque se utilice la máxima concentración de sosa cáustica, hay mezclas que no cumplen con las especificaciones de calidad del producto final por lo que este producto debe ser recirculado al proceso de neutralización para una segunda etapa de limpieza. De la tabla anterior se observa que las mezclas que necesitan de una segunda etapa de limpieza el costo unitario supera el CUC al año pues necesitarán de un mayor consumo de sosa cáustica.
Evaluando los puntos óptimos en la función de consumo de sosa se puede determinar la cantidad de sosa cáustica que se consumirá y pronosticar cada cuántos días se debe cambiar. Los resultados se muestran en la tabla 5.
Si se analiza la tabla anterior se observa que la frecuencia de cambio de la sosa cáustica se mantiene prácticamente igual que en las condiciones actuales y que en los casos en que no se logra cumplir con el parámetro de calidad establecido hay un mayor consumo de sosa.
Conclusiones
Es factible determinar las condiciones óptimas de conducción del proceso en correspondencia con el objetivo de intensificación mediante un proceso de optimización multiobjetivos.
La modelación matemática multiobjetivo puede ser utilizada en el control del proceso en refinerías de petróleo pues permite pronosticar el comportamiento de las variables controladas.
Se obtuvo que el tiempo de reacción óptimo es de 15 min con una concentración máxima de sosa cáustica de 15 ppm, es decir, 4,14 mol/L, lográndose definir el período de cambio de la sosa cáustica para cada mezcla estudiada.