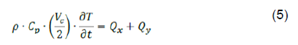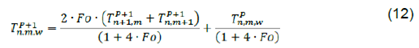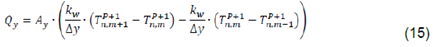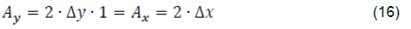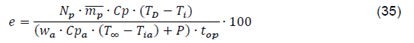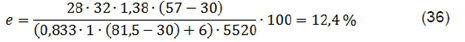Artículo original

Optimización de un sistema convectivo de aire caliente recuperado de calderas para el tratamiento fitosanitario de palets de madera (II)

Optimization of a boiler-recovering hot air convective system for phytosanitary treatment of wood pallets (II)

0000-0002-3821-5117Fredy Fong-Casas¹  , 0000-0003-1133-8683Elianne Vázquez-Montero¹  , 0000-0002-1384-0493Ángel Sánchez-Roca²  , Yudith González-Díaz³  , 0000-0002-1826-582XHarold Crespo-Sariol^{4  *} 

¹Santiago de Cuba Rum Factory, Santiago de Cuba, Cuba

²Faculty of Mechanical Engineering, Universidad de Oriente, Santiago de Cuba, Cuba

³Faculty of Chemical Engineering and Agronomy, Universidad de Oriente, Santiago de Cuba, Cuba

⁴Centre of Neurosciences Signal and Images Processing, Applied Acoustic Research Group, Universidad de Oriente, Santiago de Cuba, Cuba

RESUMEN

Este estudio es la segunda parte de un trabajo previo publicado recientemente sobre la optimización de una nueva instalación de tratamiento fitosanitario por calor convectivo aplicando el calor de los gases de escape de una caldera de destilería como fuente de energía para la desinfección térmica de los palets. En el trabajo mencionado, se aplicó un elemento de volumen de control del modelo matemático de transferencia de calor finito 3D y se correlacionó con datos experimentales para estudiar las condiciones operativas óptimas de temperatura del aire y tiempo de retención cuando se tratan térmicamente paletas tipo bloque. Sin embargo, hasta ahora no se han evaluado las condiciones óptimas para el tratamiento fitosanitario de los palets tipo stringer (los segundos más utilizados en las operaciones comerciales a escala mundial) en la instalación presentada. Este estudio de caso presenta el desarrollo y la aplicación de un modelo matemático de elementos de volumen de control de transferencia de calor finito 2D para optimizar los parámetros operativos para el tratamiento fitosanitario de palés de madera tipo stringer. La optimización de la temperatura de tratamiento y del tiempo de retención se simula basándose en los resultados comunicados anteriormente. Se encontraron las condiciones óptimas para las paletas tipo stringer con una temperatura del aire de 80°C y 95 min de tiempo de tratamiento. Se discute la eficiencia térmica, el índice de consumo energético por palets tratado en las condiciones estudiadas y la viabilidad económica del nuevo sistema de tratamiento.

Palabras-clave: transferencia de calor; elementos finitos; palets de madera; tratamiento fitosanitario

ABSTRACT

This study is the second part of a previous work recently published about the optimization a new facility for convective heat phytosanitary treatment system applying the heat of exhaust gases from a distillery boiler as energy source for the pallets thermal disinfection. In the mentioned work, a control volume element of 3D finite heat transfer mathematical model was applied and correlated with experimental data in order to study the optimal operational conditions of air temperature and retention time when block-type pallets are thermally treated. However, optimal conditions for the phytosanitary treatment of the stringer-type pallets (the second more used in world-wide trading operations) in the presented facility has not been assessed so far. This case study presents the development and application of a control volume element model of 2D finite heat transfer mathematical model to optimize the operational parameters for the phytosanitary treatment of stringer-class wood pallets. The optimization of treatment temperature and retention timeissimulated based on previous findings reported. Optimal conditions were found for stringer-type pallets withair temperature at 80°C and 95 min of treatment time. The thermal efficiency, the energy consumption index of per treated pallet at the studied conditions and the economic feasibility of the new treatment system is discussed.

Key words: heat transfer; finite elements; wood pallets; phytosanitary treatment

Introduction

Shipping pallets are essential components of global supply chains for commercial development. However, they are identified as one of the causes that have facilitated the introduction of pathogens and insects in several countries of the world.^1,2There are two main wood pallet designs: stringer-class pallets and block-class pallets.The stringer-class pallet consists of at least two stringers, multiple deckboards, and fasteners.³⁾ Pine (conifers) is the most common wood used in pallet manufacturing.⁴

The International Plant Protection Convention (IPPC) rules the “International Standards for Phytosanitary Measures 15 (ISPM 15)” on the phytosanitary treatment of all trading wood materials. IPSM 15 mandates that wooden packaging must be heat-treated or fumigated with methyl bromide.^4,5Thermal treatment is found among the mostly used authorized treatments. Heat treatment is supposed to be more environmentally friendly than fumigation, which has a detrimental effect not only on the environment but also on health.⁶ Therefore, effective heat sterilization are becoming more common.⁷ The heat treatment could be performed by means of convective or dielectric heating methods. The convective heating method is one of the most used and consists in achieving a minimum temperature of 56-57 °C for at least 30 minutes throughout the entire profile of the wood (including its core).^6,8

From the economic point of view, the cost of implementing heat treatment will be a function of the efficiency of the heating method, cost of heat energy (steam, electricity, etc.), and the initial capital costs of infrastructure.⁷⁾ Electricity (resistive) is generally the most expensive way. Burning waste wood to heat water to steam or to heat oil is so far the least expensive method.

In developing countries and especially in those which have a lack of energy resources, it is crucial to take advantage of any available energy source in order to maximize the energetic efficiency of the industrial processes, also finding solutions based on sustainable energy technologies suitable for each specific region.¹.As a background, oak casks deterioration in cellars due to xylophage insect’s invasions which came from contaminated pallets has been a continuous concern of spirit producers in Cuba. In addition, pallets fumigation is not an option of treatment due to pesticides which are strictly forbidden in food and beverages industry. Therefore, actions to find an efficient and suitable heat phytosanitary treatment of pallets for trading and storage oak barrels must be undertaken to avoid economic losses in spirit industry.¹⁾ Recently, a convective heat system for phytosanitary treatment by applying recovered heat from a distillery boiler’s flue gases was reported.¹ The new system was focussed on the elimination of pests from the pallets used for spirit trading and palletized system of natural ageing in cellars. A control volume element of 3D finite heat transfer mathematical model was applied and correlated with experimental data in order to study the optimal operational conditions of air temperature and retention time when GMA block-type pallets made of pine wood are thermally treated. The presented 3D model allowed to obtain the spatiotemporal temperature profile in the wood block and determining the overall convection heat transport coefficient in the proposed treatment facility. The model is applied for the optimization of treatment schedules to ensure that treatments are effective whilst avoiding wood structural damages and the application of energy beyond what is necessary to ensure phytosanitary compliance.¹ As conclusion, in the referred previous work, optimal conditions were found for the studied system with an air temperature at 80°C and treatment time of 137 min for pine GMA block type pallets. Although the thermal efficiency of the new proposed system operating at optimal conditions was 9,14 % (which is a typical value of this type of convective systems), the heat recovering of flue combustion gases from the boiler proved to be an effective strategy to significantly reduce (in about 12 times) the phytosanitary treatment costs with a derived economic and environmental impact.

However, optimal conditions for the phytosanitary treatment of the stringer-type pallets (the second more used in world-wide trading operations) in the presented facility has not been assessed so far. This case study presents the development and application of a control volume element model of 2D finite heat transfer mathematical model to optimize the operational parameters for the phytosanitary treatment of stringer type wood (pine) pallets. The novelty of the presented work and the new proposed approach might constitute a motivation for future researchers and wood treatment specialists to generalize and improve the presented facility design in order to increase the current treatment efficiency and its effectiveness, focussed on reducing environmental impact and support sustainable technologies for its development.

Materials and methods

Convective heat system facility

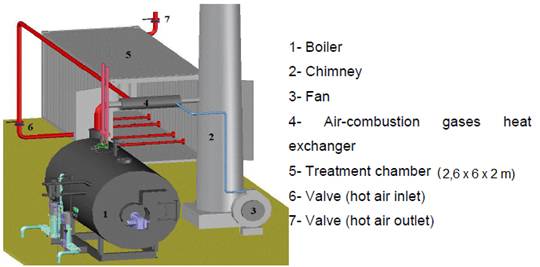
The main idea of the proposed phytosanitary treatment systemis to recover the thermal energy of the exhausted gases from a distillery boiler to heat up the treatment chamber to reach the ISPM 15 disinfection conditions. Figure 1presents the general diagram of the treatment facility.

Fig.1 Conceptual three-dimensional scheme of the studied convective heat treatment system facility 

In brief, exhausted combustion gas (260-280°C) produced in the boiler (1) is conducted to the chimney (2). In the exhaustion gas conduit, a heat exchanger (4) is installed for heating outdoor air which is supplied by the fan (3). The hot air is sent to the treatment chamber (5) and circulated through the chamber by a dedicated distribution system. The air is injected from the chamber bottom to the top taking advantage of the natural convective flow.

The heated air temperature and flow are controlled by combining the control of the fan speed and the automatic inlet and outlet valves (6) and (7). The system can provide hot air within a temperature range of 60-100°C.

Wood piece

The stringer is the thickest part of the stringer type pallet structure, thus the required time to disinfect the stringer core at the treatment temperature (56-57°C) will be the minimum time needed to ensure that all the wood pallet structures have been efficiently disinfected. In this study, the stringer considered for energy transport simulation is a piece of 100 mm high, 40 mm thick and 1200 mm long (H=100, W=40, L=1200 mm). This choice is justified by geometrical considerations since this part takes the longest time to get disinfected by the pathogen elimination temperature. The average equilibrium moisture in the stringers was considered as 11,5 % and pine wood density as 510 kg/m³⁽¹. Thermophysical properties of the pine wood for the heat transfer calculations were considered to be constant in the temperature range studied as follows: wood specific heat Cp=1, 38 kJ/(kg°C) and wood thermal conductivity k_w= 0,12 W/(m°C).^10,11

Mathematic model approach

Compared with the block type pallet (which was modelled by 3D finite element analysis on the cubic geometry), the stringer can be considered as semi-infinite solid since L((W, L((H thus a homogeneous temperature profile along the stringer (z coordinate) is considered.¹ Therefore, nonlinear heat conduction problem for the pine stringer piece is solved using 2D finite element analysis by applying control volume energy balance method which is discretized based on totally implicit model inx and y coordinates.¹⁰

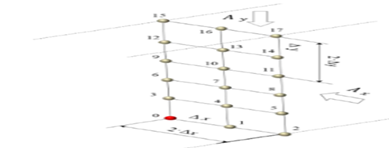
Figure 2 presents a spatial scheme of an x,y plane of the stringer section. Since the rectangular geometry has a regular symmetry, temperature profile in time domain of the whole plane can be represented byequal 1/4basic (20x50 mm)rectangular areas (bold solid line in figure 2) with a common internal vertex (the stringer core, highlighted in red).

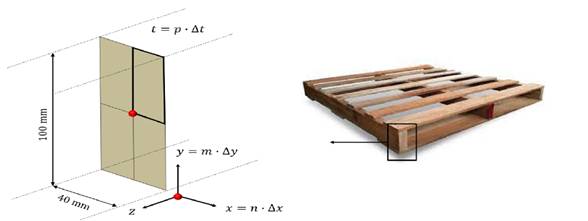
Fig.2 Spatial scheme of an plane of the stringer sectionsymmetrically divided into equal 1/4 basic (20x50 mm) rectangular sections. The stringer core as common vertex is highlighted in red 

The temperature change in time domain (t) for any nodal point (x,y,z) in the (20x50 mm) basic rectangular section can be represented in a discretized way by applying the discrete transformations as follows:

Where:

m, n, w and t are the discrete coordinate sand (y,(x and (t are the discrete differentials (steps) fory, x and z dimensions and time respectively.

Discrete differentials in all spatial dimensions were equally distributed as:

((x=(y=10 mm) in order to simplify the calculations and the applied time differential was(t=600 s (10 min).

The energy balance was performed on 2((xcubic control volume as presented in figure 3. Therefore, as(x=(y, and conveniently taking a unitary dimension for the z coordinate, the control volume (V_C) for the balance corresponds to eq.4:

Based on the reticular scheme of the control volume, a total of 18 nodes are generated for the energy balance in the 1/4 symmetrical (20x50 mm) rectangular sections of the whole (40x100 mm) plane. T₀: core temperature of the (40x100x1200 mm) stringer. The energy transport areas A_x and A_y and its flow directions (arrows) for the two dimensions are also indicated in figure 3. Based on the nodes generated in the reticular scheme in figure 3, a classification and examples of node types are displayed in figure 4.

Fig.3 Reticular scheme of a 2((x cubic control volume and generated nodes 

The nodes classification results are crucial to obtain the energy balance equations

to describe the temperature changes in time domain as it will be discussed further on.

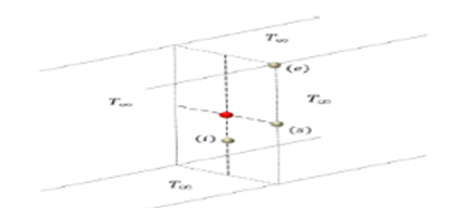
Fig.4 Examples of node types for the energy balance in the wholestringer.T₍: Environment (air) temperature into the treatment chamber 

The general energy balance equation applied on a half of V_C can be written as:

Where

(: wood density (in kg/m³)

C_p: wood heat capacity (in J/ C°·kg^-1)

T: Temperature (in C°)

t: time (in s)

Q_x, Q_y: Heat flow transported through the (x,z), (y,z)planes respectively (in W)

Then, discretizing eq.2 and combining with eq.1 gives:

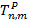: Temperature in a point of coordinates n,m in a time (t)(p

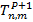: Temperature in a point of coordinates n,m in a time increment (t+(t)(p+1

The right term of the discrete energy balance (eq.6) is developed according to the node type analysed as follows.

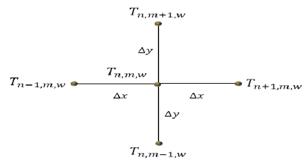
Heat transfer discrete equation for internal nodes, type (i)

For internal nodes (i) (Figure 5) the heat is transported exclusively by the conduction mechanism. Therefore, in this case the energy balances for (y,z) and (x,z) planes were conveniently discretized in a half of control volume as:

A_x, A_y: Heat flow area in the (y,z) and (x,z)planes for the control volume energy balance (in m²)

k_w: Wood thermal conductivity (in W/m·°C)

Fig.5 Reticular 2D-scheme of internal node type (i) of discrete coordinates n,m 

Having(x=(y and the same heat flow area for all the dimensions, yields:

Combining Eqs. 6, 7, 8 and 9, the temperature of any internal node of coordinatesn, mas function of the time (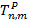 ) in the stringer piece can be determined by Eq.:

Being F_O: the Fourier number (dimensionless) which is defined by Eq.10 as:

Based on the symmetry criteria, for the wood cubic probe core (node (0)) the equation 10 can be simplified as:

Heat transfer discrete equation for surface or wall nodes, type (s)

For surface or wall nodes “type (s)” depicted in figure 6, the heat balance comprises two different mechanisms. The wall node receives the heat by convection from the hot air environment at temperature (T₍), then the heat is transported by conduction to the internal and also neighbours wall nodes on the wood piece.

Fig.6 Reticular 2D-scheme of a surface or wall node “type (s)” of discrete coordinates n,m. Dash line indicates the wall/surface plane 

Therefore, in this case, the energy balances for (y,z)and (x,z)planes were conveniently discretized in a half of control volume as:

Where:

h: Heat transport coefficient (in W/(m²·⁰C))

T₍: Air temperature in the chamber (in ⁰C)

For (y,z) plane, the heat balance gives:

Having:

Combining the general balance eq.6 with Eqs.13-16, the temperature of any wall/surface node of discrete coordinates n, mas function of the time can be determined by eq.:

With: the Biot number (dimensionless) which is defined by eq.17 as:

Heat transfer discrete equation for edge nodes, type (e):

The edge nodes can be also realized as wall border nodes in the confluence of two planes. Figure 7 presents a reticular 2D-scheme of an edge node “type (e)” of coordinates n,m. The heat transported on the edge direction can be modelled by Eq.19 and 20.

Fig. 7 Reticular 2D-scheme of an edge node “type (e)” of coordinates n,m. Dash line indicates the confluence of y,z and x,y planes to form the edge in this case 

In this case, in order to increase the accuracy and to guarantee the stability and convergence criteria, the balance is conveniently discretized to 1/4 of the control volume as:

With

Thus, combining Eqs.19-22 the temperature of any edge node of discrete coordinates as function of the time can be determined by eq.23:

Data plotting, processing, model solution and analysis were performed by applying MATLAB^® and Origin 8.1 ^® software.

Results and discussion

For convective thermal disinfection, both operational parameters: treatment time and temperature have to be analysed for the process optimization. If the air temperature increases, the treatment time decreases and vice versa. However, higher air temperature inflicts drastic thermal changes in the treated wood that could affect its original physic-chemical and mechanical characteristics. In contrast, lower air temperature is friendlier with the wood and suitable for preserving its original properties. However, the treatment time can increase significantly thus affecting the process from the economic viewpoint related with the treatment costs and the production dynamics. Therefore, the optimization of the treatment operating conditions must be addressed to find the best relationship temperature-time.

Based on the found values in the heat transfer coefficients and the imperceptible air velocity into the chamber, it was concluded that the dominant heat transfer mechanism ruling the heat transference process in the studied treatment chamber is free convection. In that case, the heat transfer coefficient for free convection at air temperature for external heat flow can be expressed by the general form.^9,10,11

Where:

L: Characteristic length of the geometry (in m)

K_w: Thermal conductivity (in W/m² °C)

C: Constant (dimensionless)

Gr_L: Grashof number (dimensionless)

Pr: Air Prandtl number (dimensionless)

n: coefficient (typically 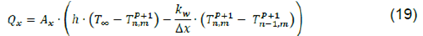=1/4 for laminar flow)

β: Air volumetric thermal expansion coefficient (in K^-1)

g: Constant of gravity acceleration (in m/s²)

(: Air kinematic viscosity (in m²/s)

T_s: Surface temperature (in K)

Thermophysical properties of the air are determined at T_f

Based on Eq.24, the ratio between heat transfer coefficients at different conditions of characteristic length of the geometry (L) withair temperatures T₍₁and T₍₂ can be expressed by a similarity ratio equation as:

L₁, L_2, Gr_L1, Gr_L2, Pr_2: Characteristic length of the geometry, Grashof and Prandtl numbers calculated at temperature conditions 1 and 2 respectively.

Thus, combining Eqs.25-28 gives:

Since the studied treatment chamber can operate in the optimizable temperature range of 60-100°Cand considering the average initial temperature of the wood stringeras T_s=30°C for tropical regions like the Caribbean, the variation of the heat transfer coefficient in function of the air temperature can be determined by the similarity eq.29 taking as reference the minimal heat transfer coefficient found in the treatment chamber at 77°C (h_77°C= 6,1 W/m².°C) reported in.¹ Additionally, differences between characteristic length of the block and stringer pallets (block: L=0,1 m, stringer: L= 0,04 m) are considered in the similarity Eq. 29.

Table 1 presents the average heat transfer coefficients calculated at different temperatures within the optimizable range for stringer type pallets.

Table 1 Heat transfer coefficients variation with the air temperature in the treatment chamber 

Based on the results obtained by Eq. 29, in the evaluated optimizable temperature range (60-100°C), the 2D finite model can be used to optimize the treatment operating conditions. Figure 8depicts the simulated heating curves of the wood core temperature in function of the treatment time by applying the 2D finite model (Eqs. 10,12, 17 and 23) within the optimizable temperature range.

Eq.29 was applied taking 77°C as reference temperature as reported in ⁽¹⁾ and correcting for stringer characteristic dimension.

Heating curves of figure 8were obtained by applying the variation of the heat transfer coefficients with the air temperature (table 1) and an average initial temperature of the wood ofT_ini. =30°C.

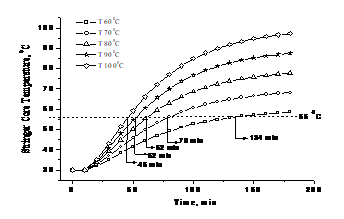
Fig. 8 Simulated heating curves of the stringer core temperature in function of the treatment time by applying the 2D finite model at different air temperature 

Figure 9 shows the derivative analysis of the change of the treatment time in function of the applied air temperature in the chamber.

Fig. 9 Derivative analysis of the change of the treatment time in function of the applied air temperature in the chamber. T_op: Optimal air temperature for the phytosanitary treatment 

The negative values of the derivative function (dt/dT) represents the amount of delayed time (in min) to reach the minimum required temperature of 56°C. From figure 9, an abrupt change in the derivative function at air temperatures below 80°C is noticeable. The optimization function is obtaining by calculating the difference between the derivative curve and the line formed by the curve’s extreme points thus mathematically determining the point of maximal slope change.

In the range of air temperature from 80-100°C, the changes in the minimum treatment time is not that significant (-1 to-2 min/°C) compared with the range 60-80°C which drops to a delay rate of almost -7 min/°C. Therefore, the optimal air temperature in the studied phytosanitary treatment facility is about 82°C. As previously discussed, the idea is to reduce the effects derived from an aggressive thermic regime in order to avoid possible damages to the wood properties but ensuring an efficient disinfection and production flow. An air temperature about 80°C is the more suitable temperature to fulfil with the optimization criteria. Therefore, optimal operating conditions for the studied phytosanitarytreatment facility are as follows: air temperature of 82°C and treatment time of 62+30 min =92 min in total. This result is in line with reported findings.¹

According to the found optimal treatment conditions, a general assessment of the efficiency and economic feasibility of the proposed system can be analysed as proposed in the literature.⁽¹⁾

The efficiency e of the treatment process in the studied system can be determined by Eq. (30)

with

E_ef: Effective energy absorbed by the wood to reach the disinfection temperature (in kJ)

E_T: Total energy consumed to maintain the system at optimal temperature (in kJ)

Where

Np: Number of GMA type pallet (load capacity) per treatment [N_p= 28]

m_p: Average of string type pallet weight (in kg) [m_p= 32 kg]

T_D: Disinfection temperature (in °C)[T_D= 57 °C]

T_i: Average of initial temperature of the wood (in °C) [T_i= 30 °C]

On the other hand

E_h: Thermal energy consumed for heating the air (in kJ)

E_e: Electrical energy consumed by the fan to feed the hot air (in kJ)

With

w_a: Mass air flow supplied by the fan (in kg/s) [w_a =0.833 kg/s]

t_op: Optimal treatment time (in sec) [t_op= 92 min = 5520 s]

C_Pa: Air heat capacity (in kJ/ C°·kg^-1)[C_Pa( 1 kJ/ C°·kg^-1]

P: Electrical power consumed by the fan (in kJ/s) [P= 6 kJ/s]

T_ia: Average of initial (atmospheric) air temperature [T_ia= 30 °C]

Combining eqs. 31- 34 gives

Calculating the efficiency of the studied treatment system under the specific conditions gives

The found efficiency for the studied system is in line with reported values of other convective heat systems where the thermal efficiency can range between 7% and 13 %². For instance, Kumar D. et al. (2022) ¹¹⁾ reported a thermal efficiency of 10,67 % for a dedicated design of a biomass-fired grain dryerwith flue gas thermal energy recovering and thermal efficiency for GMA block type pallet was found around 9 % as reported in¹.

However, as in the studied system the thermal energy to heat the air in the chamber is coming from the exhausted combustion gases of the boiler, it does not have any influence on the process cost. On the other hand, the consumed electricity by operating the fan during the treatment time represents the main energetic cost in the process.

In this case, the electric energy consumption index (I_HT) in kWh per stringer type pallet treated was determined by Eq.(37)

Energetically speaking, stringer pallets treatment is more efficient compared with block type GMA pallets.¹ The stringer geometry permits the heat transport to the wood core faster than in a block piece thus reducing significantly the treatment time consumed and therefore increasing the treatment efficiency.

Conclusions

The presented treatment facility consisting of a heat recovering process of exhaust gases from boilers demonstrates to be an efficient and economical solution to guarantee wood pallets disinfection according to ISPM 15 regulations. The major findings of this study can be concluded as follows.

The application of a control volume element model of 2D finite heat transfer method prove to be a useful tool to simulate and optimize the operational parameters of convective treatment by air temperature and residence time. From this modelling study, not only it is possible to calculate the time required to reach the disinfection temperature of 56 -57°C but also to predict the reliability of the convective phytosanitary treatment and assess the heat distribution effectiveness in the treatment chamber.

Optimal conditions were found for stringer type pallet treatment in the studied system with an air temperature at 81,5°C and treatment time of 92 min. Based on simulated results, heat treatment for stringer type pallets is more energetically efficient compared to GMA block type pallets.

This mathematical approach is not limited to the presented conditions thus can be used as tool for assessing heat treatment systems for different wooden materials, convective heating systems and geometries.

Acknowledgments

The authors would like to thanks the VLIR-UOS project between Belgium and Cuba for providing funding and granting the support of the current and future studies.

References

1.  FONG CASAS, Fredy, et al1.  . 3D finite heat transfer method to optimize a hot air convective system for phytosanitary treatment of wood pallets. Energy, Ecology and Environment1.  , 2023, p. 1-15. Available in: https://link.springer.com/article/10.1007/s40974-023-00275-81.

2.  KIM, Kang-Jae, et al2.  . Characteristics of the hest treated wood pack aging materials according to international standards for phytosanitary measures and verifiability of heat treatment. Wood research2.  , 2019, 64(4), p. 647-658. Available in: http://www.woodresearch.sk/wr/201904/08.pdf2.

3.  PARK, Jonghun; HORVATH, Laszlo; BUSH, Robert J. Life cycle inventory analysis of the wood pallet repair process in the United States. Journal of Industrial Ecology3.  , 2018, 22(5) p. 1117-1126. Available in: https://onlinelibrary.wiley.com/doi/abs/10.1111/jiec.126523.

4.  DEVIATKIN, Ivan, et al4.  . Wooden and plastic pallets: A review of life cycle assessment (LCA) studies. Sustainability4.  , 2019, 11(20), p. 5750. Available in: https://pdfs.semanticscholar.org/b2be/eacb52d2132250614daf603fd6a95049dcdf.pdf4.

5.  PAWSON, Stephen M., et al5.  . Flight activity of wood-and bark-boring insects at New Zealand ports. New Zealand Journal of Forestry Science5.  , 2020, 50. Available in: https://nzjforestryscience.nz/index.php/nzjfs/article/view/1325.

6.  BEDELEAN, Bogdan. Application of artificial neural networks and Monte Carlo method for predicting the reliability of RF phytosanitary treatment of wood. European Journal of Wood and Wood Products6.  , 2018, 76(4), p. 1113-1120. Available in: https://link.springer.com/article/10.1007/s00107-018-1312-16.

7.  PAWSON, S. M., et al7.  . Quantifying the thermal tolerance of wood borers and bark beetles for the development of Joule heating as a novel phytosanitary treatment of pine logs. Journal of Pest Science7.  , 2019, 92, p. 157-171. Available in: https://link.springer.com/article/10.1007/s10340-018-1015-87.

8.  FRĄŚ, Józef; OLSZTYŃSKA, Ilona; SCHOLZ, Sebastian. Standardization and certification of the wooden packaging in international trade. Research in Logistics & Production8.  , 2018, 8, p. 25-37. Available in: https://yadda.icm.edu.pl/baztech/element/bwmeta1.element.baztech-97761fc2-4f97-4a3f-995e-ce8e8604bfab8.

9.  - JEFFERS, Ann E. Heat transfer element for modeling the thermal response of non-uniformly heated plates. Finite Elements in Analysis and Design9.  , 2013, 63, p. 62-68. Available in: https://www.sciencedirect.com/science/article/abs/pii/S0168874X120016559.

10.  INCROPERA, Frank; DeWitt, David. Fundamentals of heat and mass transfer10.  .6th edition. United Statesof America: John Wiley and Sons Inc., 2007. 1070 p. ISBN: 978-0-471-45728-2

11.  KUMAR, Dhananjay; MAHANTA, Pinakeswar; KALITA, Pankaj. Performance analysis of a novel biomass-fired grain dryer integrated with thermal storage medium. Biosystems Engineering11.  , 2022, 216, p. 65-78. Available in: https://www.sciencedirect.com/science/article/abs/pii/S153751102200027711.

Conflicts of interest

0Author’s contribution

Recibido: 10 de Mayo de 2023; Aprobado: 18 de Agosto de 2023

^*Author for correspondence. Mail:[e-mail]

The authors declare that there are no conflicts of interest

Fredy Fong-Casas: conceptualization, field work, data curation, formal analysis, writing - original draft.

Elianne Vázquez-Montero: field work, formal analysis

Ángel Sánchez-Roca: data curation, supervision review & editing.

Yudith González-Diaz: conceptualization, formal analysis, supervision, writing - review & editing.

Harold Crespo-Sariol: conceptualization, data curation, formal analysis, supervision, writing - review & editing.