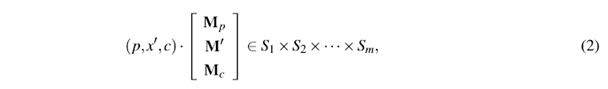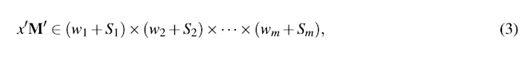Introduction
The Genetic Algorithm (GA) is a heuristic optimization method based on biologic genetic evolution. A successful application in cryptanalysis to block ciphers has been achieved. Some of the research carried out in this direction is mentioned below. The aim of (Mittal and Gupta, 2019) is to establish an algorithm for encry ption and decryption of a message based on symmetric key cryptosystem involving GA and its operators. In (Abduljabbar et al., 2021) a fast technique for text encryption depending on GA and its operators is presented. In (Nofal, 2022) an optimization problem, associate with the Internet of Things, is solved using GA. In (Aas- hiqbanu et al., 2022) authors propose a hybrid Telugu cryptography based on GA by mapping it in Unicode. Confusion and diffusion are performed to strengthen the algorithm’s security in four stages: pre-processing, reshape, crossover and mutation. The papers (Qiu and Wang, 2022) and (Artuger and Ozkaynak, 2022) are similar: authors propose to use the GA to search cryptographically significant substitution box: S-boxes. The idea is to find resistant S-boxes against different attacks. Other details about GA can be seen in (Katoch et al., 2021), (Tito-Corrioso et al., 2021) and (Cao et al., 2022).
On the other hand, we focus on algebraic cryptanalysis, characterized by the formulation of the attack problem as the solution of a system of equations. Representing ciphers as a system of equations can be done in diffe rent ways, in particular, the focus of this work is on Multiple Right Hand Side, MRHS, equations systems, introduced in (Raddum and Semaev, 2006) These systems are an alternative method for algebraic work with block ciphers. Its main peculiarity is that the independent term is not unique for each equation, but rather, it is a set of independent terms. Actually there are several paper about this topic. For example, in (Zajac and Spacek, 2019) authors propose a new concept of (post-quantum) digital signature algorithm derived from a symmetric cipher which security is based on the difficulty of solving MRHS equations and key derivation is based on this systems. The focus in (Indr0y and Raddum, 2021) is the problem of evaluating a block cipher’s strength against differential or linear cryptanalysis via Compressed Right-Hand Side equations, which are MRHS equations where the right-hand sides are stored using a binary decision diagram instead of multiple independent vectors. Further details on the theory of MRHS systems can be found in (Indr0y, 2018), (Matheis et al., 2019) and (Zajac, 2021).
This paper presents a first approach to the subject of MRHS systems and the use of the Genetic Algorithm as a method of solving them. Searching for the solution in the entire space is increasingly difficult as the number of variables increases, for this reason, the use of two partition methodologies is also proposed of the space, which allow to focus the search on one or several subsets of the complete space. On the other hand, three fitness functions are proposed that allow connecting the MRHS systems with the GA. The experiments showed good results in the solution of the MRHS systems by GA.
Materials and methods
Genetic Algorithm
GA is a heuristic optimization method. We assume that the reader knows the general ideas of how the Genetic Algorithm works. This section we will briefly describe the GA scheme used in this work.
Algorithm 1 Genetic Algorithm
Input: m, number of individuals in the population; F, fitness function; g, number of generations; s, number of individuals selected to mate.
Output: the individual with the highest fitness function as the best solution.
1: Generate randomly an initial population Pi with m individuals, possible solutions.
2: Calculate the fitness of each individual of P i with F.
3: while no solution found or g generations not reached do
4:Select s parents of Pi.
5: Perform the Crossover of the s selected parents and generate offspring pairs.
6:Mutate each of the resulting descendants.
7:Compute the fitness of each of the offspring and their mutations with F.
8: Using the Tournament Method between two, based on the aptitudes of the parents and offspring, decide what will be the new population Pi+1 for the next generation, selecting two individuals at random each time and choosing the higher fitness.
9: end while
The individuals of the populations will be elements of the key space taken as binary blocks. By Selecting the s parents, a subset S of P i is obtained. These parents are selected by the Tournament Method between two, selecting two individuals at random and choosing the one with the highest aptitude. Elements of S are crossed, and descendants are added to P i if they are not members. For Crossover the two-point crossover will be used, and the probability of two individuals crossing over was set to 0.6 for all experiments. The Mutate operation consists of making changes to at most three random components of the binary block, with a mutation ratio set to 0.2 in all experiments. An individual x is better adapted than another y, if it has greater fitness, that is, if F(x) > F(y). The fitness functions with which we make the connection between the GA and the MRHS equations systems will be defined in next sections. For the GA specification to block ciphers, see Section 3 of (Borges-Trenard et al., 2019).
This application of GA in Cryptography constitutes a known-plaintext attack model proposal, in which the attacker knows a set of plaintexts with their corresponding encrypted texts. The attack’s goal is to find the key with which the plaintexts were encrypted.
Key space partition methodologies
Key space partition methodologies allow the GA to work on a certain subset of the set of admissible solutions as if it were the full set. The importance of this fact is that it reduces the size of the search space and gives the heuristic method a higher chance of success, assuming that the fittest individuals are found in the selected subset. On the other hand, the partition into equivalence classes allows it to use the GA or another algorithm in parallel, in several classes simultaneously.
The first methodology is the BBM, proposed in (Borges-Trenard et al., 2019). Let F^1 be the space of keys of length k 1 G Z>0. It is known that F21 has cardinal 2kl and therefore there is a one-to-one correspondence between F21 and the interval [0,2k1 - 1] c Z+. If an integer k2 is set, (1 < k2 < k1), then the key space can be represented by the numbers, q2 k2 + r, where q G [0,2k1-k2 - 1] c Z+, and, r G [0,2k2 - 1] c Z+. In this way the key space is divided into 2k1-k2 blocks, determined by the quotient in the division algorithm dividing by 2k2, and, within each block, the corresponding key is determined by its position, which is given by the remainder r. The main idea is to position yourself in a block, given by q, and move within that block through the elements, given by r, using the GA.
The next methodology is the TBB, proposed in (Tito-Corrioso et al., 2019) and (Tito-Corrioso et al., 2021). This methodology is based on the definition and calculation of the quotient group of keys GK whose objective is to partition F^1 into equivalence classes. It is known that F^1, as an additive group, is isomorphic to Z2q. Let h be the homomorphism defined as follows: h: Z2q -/ Z2k2, s.t. a -> a (mod 2k2), where k2 G Z>0 and 0 < k2 < k1. Let us denote by N the kernel of h, then, GK is the quotient group of Z2k1 times N, that is, Gk = Z2k1 /N. And finally, GK = {N, 1 + N, 2 + N,..., (2k2 - 2) + N, (2k2 - 1)+ N}.
In this way Z2k1 is divided into a partition of 2k2 classes given by N. To iterate through the elements of each class, note that Z2k2 is isomorphic with GK and the isomorphism corresponds to each r G Z2k2 its equivalence class r + N in GK. Therefore, selecting a class is setting an element r G Z2k2. On the other hand, the elements of N have the form q2k2, q G {0,1,2,..., 2k1-k2 - 1}, therefore, the elements of the class r+N have the form, q 2k2 + r.
The idea of partitioning in the context of MRHS equations systems is, on the one hand, to decrease the search space for solutions, which in the general case is F2, where n is the number of variables; and on the other hand, allow parallel search in different classes. In this case we speak of space of solutions and not space of keys, although these spaces have the same structure.
MRHS Equations Systems
Vectors over F2 will be row vectors. For more details on the theory of MRHS systems see (Raddum and Semaev, 2008) and (Raddum and Zajac, 2018).
Definition 1 An MRHS equation over F2 is an expression of the form, xM e S, where M is a matrix n x l, and S C F2 is a set of vectors of l bits. A vector x e F2 is said to be a solution of the MRHS equation, if and only if, xM e S.
A system of MRHS equations, M, is a set of m MRHS equations with the same dimension n: number of variables. That is, M = (xM; e Si11 < i < m}, where each M; is a matrix n x l i , and S i C F2. The vector x e F2 is a solution of the system M, if it is a solution of all the equations in M, this is, xM; e S ; , Vi e {1,2,..., m}.
Given a system of equations M = {xM; e S;| 1 < i < m}, they can be concatenated by the columns all the M; matrices, taking into account that they have the same number of rows, variables. The resulting matrix is called the united system matrix, and is represented as M = [M1 |M2|... |Mm ]. The columns of M that correspond to M i are called block. In the same way, the Cartesian product of all the right sides S ; is carried out, to obtain a single set S = S 1 x S2 x ••• x S m . The problem of solving a system of MRHS equations can now be stated as, find some x e F2, such that, xM e S.
The ciphers that can be represented as a sequence of linear, or affine, transformations, and substitution layers performed by S-boxes, can be represented by a system of MRHS equations as follows. Let s be the number of S-boxes per round; l a and l o the number of input and output bits of the S-boxes; nR the number of rounds; n B the size of the plaintext and ciphertext; and n K the key length. The parameters of the MRHS system are: li = l a + l o , |S;| = 2la, m = s ■ n R , and n = 2n B + n K + ml o . The vector of variables x e F2 of the system consists of the n B bits of the plaintext (x1,...,x 2b ), n K bits of key (x2B+1,. ..,x 2B + 2K ), all outputs of the S- boxes (x 2B + 2K+1 ,...,x 2-2B ), and the n B bits of the ciphertext (x2-2B+1,...,x2 ). If S-boxes are used in the key generation scheme, they are considered as part of the encryption. All input bits of all S-boxes can be described as linear, or affine if there is addition of constants, combinations of the variables defined above. From each S-box i an MRHS equation is created as follows,
where c is the constant input part of the affine combination, using the natural conversion between the integers and the vectors of F2. The first l a columns of M; contain the coefficients of the linear combination of the input to the S-box. The last l o columns contain a single bit 1 each: mj,t = 1 if xj is the variable for output bit t after multiplication, and mj,t = 0 otherwise.
When the objective of building the united matrix of the system is to do an algebraic cryptanalysis, focused mainly on the search for the key, then we assume that the pair of plaintext and ciphertext is known. Thus the system can be reduced by setting the first and last nB variables to x as follows. If the original joined system is xM e S, then it can be written as,
where p and c are the known values of the plaintext and ciphertext pair, and xX are the remaining variables. Calculated, pMp + cMc = w = (w 1 , w2,..., wm), the reduced MRHS system is obtained:
where, w; + S; = {w + v|v e S;}. Note that the scalar operations are performed on the finite field F2.
Results and discussion
Solution of MRHS equations systems using GA
To work with MRHS systems, a toolbox of functions were implemented in Maple 17 that serve as a tool for manipulating these systems of equations. Below we describe some of the functions. The GA operations are carried out on the elements of the solution space of the MRHS system without any operation of the MRHS system intervening. Where the MRHS system only comes into play is when the GA assesses the suitability of each item. In this sense, two fitness functions are proposed through which the connection between the GA and the system is made. Given a vector x e F", M and S, the first fitness function is defined as follows:
where l is the number of columns in M, and hmin is the minimum Hamming distance, d, between xM and each of the vectors of S, more formally, hmin(xM, S) = min{d(xM, v)|v G S}. Let [Y] dec be the corresponding conversion to decimal of the binary block Y, the second fitness function is:
where, g(xM, S) = min{abs([xM]dec - [v]dec)|v G S}. These functions, in short, what they do is take the sma llest distance between xM and the set S as the best solution. Note that, Hi (x), H2(x) G [0,1] C R.
Experiments and results
Experiments were performed on a Laptop PC with processor: Intel(R) Celeron(R) CPU N3050 @1.60GHz (2 CPUs), ~ 1.6GHz and 4GB RAM. The experiment consists of generating 20 MRHS systems randomly, and verifying if the GA is able to find one or several solutions for these systems. This GA search was performed with each of the two fitness functions for all generated MRHS systems. These systems have n = 16 variables and 3 MRHS equations each. The 3 blocks of M have 3, 4 and 5 columns respectively, so M has a total of 12 columns and 16 ■ 12 = 192 items. The sets S1, S2 and S3 have 4, 5 and 6 elements each, so the product set S = S1 x S2 x S3, has 120 elements. Regarding the GA parameters, the number of individuals in the population is 50. The search will be done by dividing the space with the BBM methodology, where k1 = n = 16, and k2 = 12. With these data, in total, the GA must go through at most 81 generations for each system.
The results obtained for each of the fitness functions are as follows: with the function H1, an average of 4.1 different solutions per system was found, in an average time of 0.64215 seconds and only reaching 1.05 generations; the H2 function found an average of 3.4 different solutions per system, in an average time of 3.78125 seconds and in 1.15 generations on average. Neither function was flawed, in the sense that they found at least one solution on each system. As can be seen, the GA not only solves MRHS systems, but is also capable of finding more than one solution.
Note how in the small dimensions of the developed experiments it happens that several generations of the GA are practically not necessary to obtain the solutions. In addition, short times are obtained, which allows evaluating the possibilities of this tool for the cryptanalysis of block ciphers in two fundamental directions. The first is that GA can be an effective method of finding solutions for MRHS systems. The second is that the computation time behaves well according to the algebraic nature of the problem under study.
Improving search in S
It has already been shown that with the functions H 1 and H2 solutions of the MRHS systems are found. However, they present difficulties as the number of elements in S increases. The problem is that, in order to evaluate them, it is necessary to go through S completely. As |S| becomes larger, the time consumed by each function, and therefore by the GA, also grows considerably. In this sense, in this section a methodology is proposed to improve the evaluation and search of the elements of S.
It proceeds as follows. A set S' is calculated whose elements s i , i = 1, |S'|, are those of S converted into their decimal expression. Then S' is ordered such that, if i < j, then, si < Sj, Vsi, Sj E S'. The improved Binary Search Algorithm will be applied to S', to search for [xM]dec. The objective is to obtain n such that, s n < [xM]dec < sn+1. That is, get the smallest range of elements where [xM]dec is found, which includes the case where the element sn+1 is same as searched. Then, the fitness function H2(x) is applied, passing the set L = {sn, sn+1} to the distance g, or be, g(x,L). To avoid confusion in the notation and in the procedure, the function will be denoted as H3:
where, g(xM,L) = min{abs([xM]dec - v) |v e L}.
Enhanced Binary Search Algorithms are a well-known tool in areas such as programming, computational complexity analysis, efficient database searches, etc. We will just describe it briefly. To carry out the search, it is assumed that the elements must be ordered. It consists of dividing the search interval into two parts, comparing the element sought with the central one, in case they are not equal, the extremes of the interval are redefined (depending on whether the central element is greater or less than the one sought) reducing the search space. The process ends when the element is found or, if not found, the most restricted subinterval within the initial search interval, to which the element sought belongs, is returned.
The idea is to compare the searched number a with the element in the middle of the list where the search will be performed. If equal then we find the element, if not, when a is less than the middle element the same strategy is applied to the list to the left of the middle element. And if a is greater than the element in the middle, the same strategy is applied to the list to the right of said element.
In the Maple 17 program, it is not necessary to implement this algorithm, since it has several built-in functions that allow binary search to be performed. These include BinarySearch and BinaryPlace, both from the List Tools package. As well as the sort function for sorting lists. To obtain the n sought that meets the condition, s n < [xM]dec < sn+1, the function BinaryPlace.
Note that in essence, H3 is looking for the smallest decimal distance. In this case, s n and sn+1 are the two closest elements to [xM]dec. If, [xM]dec = sn+1, then xM e S, otherwise takes the smallest distance between [xM]dec and the closest element of s n and sn+1. The main advantage is that it is not necessary to iterate through all the elements of S exhaustively. The operations to obtain S' are performed in the pre-calculus stage.
Experiments and results
The GA was applied to the same 20 systems in previous experiments, under the same conditions, but using the H3 function. As result, 3.7 solutions were found on average, in one generation in all systems and in a time of approximately 0.448 seconds. Note that the number of generations is less than that obtained with H1 and H2. The number of solutions is very similar in all three cases, and greater than with H2. The interesting thing is the decrease in the time consumed, less than with the two previous functions, and in no case did it exceed 0.5 seconds.
Other experiments with larger systems are described below, with the aim of comparing the functions H1 and H3, these two being the fastest. In all cases, the GA parameters are the same as those in previous experiments in this paper. 40 MRHS equations systems were randomly generated, with n = 16 variables and m = 4 MRHS equations each. The sets S1, S2, S3 and S4 each have eight elements, so S has 4096. The 40 systems were divided into two groups of 20 systems each: GI and GII. In the GI group the four blocks of M have four columns, so M has 16 columns in total. In group GII, M has 24 columns. In other words, increasing the number of columns in M increases the size of the space that contains the total number of elements that the set S can take. In this sense, the more the columns of M increase, keeping the other parameters fixed and especially the cardinal of S, the more difficult it is to find a solution for the MRHS system.
The results for the GI group are shown in Table 1. The second column is the number of solutions per system; the third is the number of generations in which those solutions were found, and the fourth column is the average time, in seconds, that the GA took in that number of generations.
Table 1 Results obtained with the GI group systems
| Function | Solutions | Gen. | Time (s) |
|---|---|---|---|
| Hi | 8.4 | i | 15.482 |
| H3 | 8.4 | i | 0.515 |
Note that the two functions had the same results in terms of number of solutions and generations. However, there is a big difference in the time consumed, with H3 being on average 30 times faster than H 1 . The results for group GII are shown in Table 2. In this case the times are given in minutes. Unlike Table 1, another column is added, in which the number of systems for which the GA did not find a solution is reflected. In the cases where no solution was found, and therefore the GA went through the 81 generations, the times were approximately 13.7 and 0.42 minutes for H1 and H2, respectively. The H3 function was more effective in the four comparison criteria, but above all, the main difference is again in relation to time. In this sense, H3 never reached 0.5 minutes (30 seconds), when H1 needed more than 10 minutes on average.
Table 2 Results obtained with the GII group systems
| Function | Solutions | Gen. | Time (min) | Faults |
|---|---|---|---|---|
| Hi | 0.5 | 59.05 | 10.023 | 10 |
| H3 | 0.55 | 52.05 | 0.2726 | 9 |
The two functions were tested with a much larger random MRHS system than the previous ones. The system has n = 64 variables and m = 4 equations. M has a total of 32 columns, and S has 65536 elements. The H3 function found a solution, and the total time to traverse all 81 generations was approximately 1.15 minutes. In contrast, with H2 the search was interrupted after eight hours of compilation.
In summary, it is interesting to note that with the H3 function methodology, it is possible to considerably reduce the time consumed by the GA, maintaining the same level of effectiveness in terms of the number of solutions, generations, and times when no solutions are found (failures). In other words, you gain speed without sacrificing any of the other criteria.
Conclusions
MRHS systems constitute a novel alternative method for algebraic work with block ciphers within Algebraic Cryptanalysis. The proposal of GAs as a solution method for MRHS systems is still a young line, but with promising results. With the experiments carried out and the fitness functions proposed, it is shown that the GA not only solves the MRHS systems, but that it is capable of finding more than one solution. With one of the fitness functions proposed, H 3 , it is possible to considerably reduce the time consumed by the GA in the search for solutions. In future research, we will work on modeling specific block ciphers as MRHS equations systems, and then carry out attacks on the encryption looking for the key as a solution of the MRHS system through the GA.