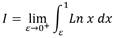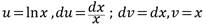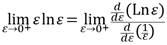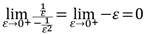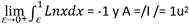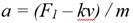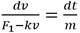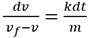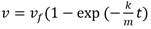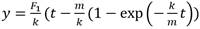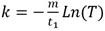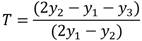Artículo original

Problemas integradores en la formación del ingeniero en metalurgia y materiales

Integrative problems in the training of the engineers in metallurgy and materials

0000-0003-0798-8296Leandro López Rubira^{1  *}  , 0000-0002-3159-0221Lierli Oconnor Montero¹  , 0000-0002-0903-5678Isora María Arcia Rivero² 

¹Universidad Tecnológica de La Habana “José Antonio Echeverría”, Cujae. La Habana, Cuba

²Centro de Investigación para la Industria Minero Metalúrgica. La Habana, Cuba

Resumen

En la formación de ingenieros es esencial desarrollar la capacidad de resolver problemas desde la matemática, la física y las ciencias de la ingeniería. Formular problemas para el aprendizaje es una necesidad permanente. En el presente artículo se asume como objetivo ofrecer una alternativa didáctica en el desarrollo del proceso de enseñanza - aprendizaje para generar sistematización del contenido y desarrollar la capacidad de resolver problemas. Como resultado, se obtienen dos problemas y sus soluciones; se da una alternativa de laboratorio asociado a la solución del segundo problema, que se presenta con una componente experimental y una con empleo de hoja Excel en la que se simula el experimento; todo ello empleado en la formación del ingeniero en metalurgia y materiales.

Palabras-clave: problemas; enseñanza; ingeniería

Abstract

During the training of engineers, it is essential to develop their skills to solve problems applying their knowledge of Mathematics, Physics and engineering sciences. To formulate problems is a permanent necessity for learning. This article is aimed at offering a didactic alternative for the development of the teaching-learning process of engineers to generate the systematization of content and the development of skills to solve problems. As a result, two problems and their solutions are obtained; a laboratory alternative associated to the solution of the second problem is presented, with an experimental component and one using an Excel sheet, in which the experiment is simulated; all results in the training of the engineer in metallurgy and materials are used.

Key words: problems; teaching; engineering

Introducción

Acerca del proceso de enseñanza - aprendizaje son conocidos los resultados teóricos siguientes:

• Se requiere una permanente sistematización del contenido de enseñanza ^[1]

• La resolución de problemas (RP)es una alternativa didáctica para desarrollar el proceso de enseñanza -aprendizaje ^[2], ^[3]

• La teoría de la actividad sirve de base teórico-metodológica para la investigación educativa dedicada a la organización el proceso de enseñanza-aprendizaje ^[4].

Los postulados anteriores son coherentes con experiencias docentes de los autores y bases de las reflexiones que en el presente artículo se describen.

En la formación del ingeniero hay una máxima compartida por todos: la enseñanza de la ingeniería se desarrolla a partir de la alternativa de resolver problemas. Referente a esta alternativa pueden ser encontradas otras propuestas ^[5]. Hay autores que defienden esta concepción, la que ha dado en llamarse enfoque investigativo y que es coherente con lo que se conoce como la aplicación del método de la ciencia. En este enfoque investigativo, los problemas tienen carácter de instrumento para lograr el aprendizaje en un marco de socialización ^[6], ^[7].

El tratamiento de un problema en la docencia para la formación del ingeniero se debe caracterizar, a juicio de estos autores, por lo siguiente: el profesor es conocedor del método y la solución, o al menos una solución, se presenta la situación problemática como si no tuviera disponible tales recursos, se realiza la formulación del problema y finalmente se construye, en socialización, la solución. Un tratamiento de este tipo está en correspondencia con las concepciones actuales de la enseñanza basada en problemas. Plantear problemas en el proceso docente puede tener muchas pretensiones, una de ella y quizás la más importante, está dada por el interés en desarrollar la competencia de problematizar, asociado a la intención de sistematizar conocimientos de un tema o una asignatura. Esto lo dicta, en primera instancia, el objetivo del proceso docente ^[8], ^[9].

La referencia de los autores al término sistematización del conocimiento en el proceso de enseñanza-aprendizaje está en relación a lo que se establece en la teoría de la lógica dialéctica y en la teoría de sistemas. Aquí se trata esencialmente de reiterar aplicaciones para dar lugar a un sistema de conocimientos en la cultura del estudiante tras asimilar conceptos, métodos y habilidades lógicas ^[10], ^[11].

A pesar de los postulados anteriores, en el contexto de este artículo no se pretende teorizar en materia de enseñanza basada en problemas, por lo tanto no se presentan conceptualizaciones en esta área, tampoco se pretende teorizar desde la perspectiva de la sistematización en el sentido de las relaciones inclusivas tema - asignatura - disciplina - carrera. Lo que se pretende es potenciar la idea de que el tratamiento de un problema docente adecuadamente seleccionado, puede dar lugar a una excelente ocasión de sistematizar conocimientos del contenido de enseñanza y desde esta relación contribuir al desarrollo de la capacidad de resolver problemas.

Esta pretensión está asociada a reflexiones acerca de experiencias históricas de los autores durante el proceso de enseñanza-aprendizaje en la formación del ingeniero en metalurgia y materiales, y es esencialmente reflexiva. Las reflexiones se dan en ocasión de tener la posibilidad real de participar en la formación de un futuro ingeniero y considerar la necesidad de realizar un modesto aporte a las potencialidades del futuro egresado de la carrera para resolver problemas.

Las dimensiones objetivas y subjetivas comentadas en el párrafo anterior se dan en la interpretación que realizan los autores del proceso formativo como objeto de estudio y tienen origen en la identificación de los hechos siguientes:

• En el diseño curricular de la carrera está presente la categoría problema, no así en disciplinas, asignaturas y temas. Así, en favor de homogenizar el proceso docente, es recomendable diseñar y plantear problemas en todos los niveles organizativos del proceso formativo.

• En los modelos de trabajo metodológico de la carrera no se identifican alternativas en las que se considere el tratamiento didáctico de problemas. Lo más cercano son las guías para la práctica laboral - investigativa.

• Dado que en la resolución de problemas en ingeniería se requiere considerar presupuestos desde varias ciencias e integrarlos en la solución, es sugerente entonces desarrollar alternativas didácticas para tal propósito.

En correspondencia a la pretensión y situación problemática anteriores se muestran dos ejemplos de problemas docentes en la enseñanza de la ingeniería en metalurgia y materiales, en cuyas soluciones contienen respectivas muestras de la sistematización del conocimiento de temas. La presentación de estos problemas está determinada por el objetivo que se han propuestos los autores, a saber, ofrecer una alternativa didáctica en el desarrollo del proceso de enseñanza - aprendizaje para generar sistematización del contenido, y desarrollar la capacidad de resolver problemas.

Existen otras alternativas de estructuración del proceso que igualmente permiten sistematizar conocimientos o métodos como son los casos de seminarios integradores y propuestas tecnológicas para procesos estudiados curricularmente. La propuesta de ocasión se distingue de otras por su acercamiento a la ingeniería y por la integración de recursos tales como el experimento real, su simulación, el modelado y recursos informáticos. Esta es la esencia metodológica en la concepción de la alternativa didáctica que se propone.

Desarrollo

Problema 1: De la realización del cálculo infinitesimal unidimensional con funciones exponenciales y logarítmicas ^[12], ^[13].

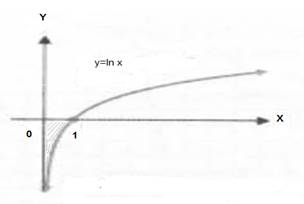
Se plantea la situación problemática siguiente: De la función f(x)= Ln (x) (x( R,x > 0), esbozar el gráfico de la función y, de ser posible, calcular el área de la región del cuarto cuadrante comprendida entre los ejes coordenados y el gráfico de la función.

En socialización en el aula se llega a los resultados siguientes: El conocimiento de la función f(x) = Ln(x) y la correcta interpretación de la situación conduce a la representación geométrica siguiente (figura 1):

Fig. 1 Área de una región plana no acotada 

Dado que se obtiene una región no acotada se busca el modelo integral adecuado. Se induce la aplicación de los modelos integrales para calcular este tipo de área y en este intento resulta el modelo integral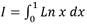

Se induce el análisis siguiente: el signo de la función no permite definir de manera directa el área y entonces hay que conceptualizar A =/I/. Esto significa que se requiere calcular la integral y con ello la primera operación infinitesimal. Pero sucede que la integral es impropia del tipo 2 (función no continua y no acotada en el intervalo) por lo tanto su cálculo es según el método siguiente:

Ahora se está en presencia de la operación cálculo de límite. El cálculo de la integral se realiza por el método de integración por partes según las conocidas expresiones:

En el empleo de este método se reitera la operación de integración y aparece por vez primera la operación de diferenciación. Al plantear la expresión del método de integración por partes se obtiene: . Esto brinda la oportunidad de realizar la operación de calcular límites, así se obtiene:

El límite de la expresión conduce a una indeterminación del tipo 0 (( y para resolver este problema se realizan las conocidas transformaciones algébricas para posteriormente aplicar el método de Regla de L´Hospital. Desde esta regla se tiene que:

Esta aplicación da la oportunidad de derivar las funciones f(x) = Ln x y g(x) = 1/x, para obtener: f´(x) = 1/x y g´(x) = -1/x2. Así, al realizar estos cálculos se están sistematizando reglas de la derivación. Los resultados obtenidos permiten escribir:

.

De aquí que: .

Se propone retomar la integral original 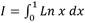y se plantea el cálculo por el método de integración por sustitución según: u = Ln (x), o sea x = e ^u y por lo tanto dx = e ^u du. Se obtiene que: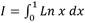

En la realización de esta transformación se considera el gráfico de la función logarítmica para poder decidir los nuevos límites de integración. Ahora se presenta una integral conocida en la que para su cálculo se emplea el método de integración por partes y antes se solicita identificar la función a integrar e intentar esbozar su gráfico ya que la función f(x) = xex fue tratada en ocasión del tema Análisis de curvas y solo hay que recuperar, según alguna heurística, sus propiedades con su gráfico, de ello resulta:

• Dominio: x ( R

• Imagen: Desconocida en un primer momento

• Interceptos con los ejes: (0,0)

• Extremos y monotonía: f´(x)= (x+1) ex=0 esto implica que x= -1 es el único punto posible de extremo. Si x > -1 entonces f´(x) > 0 y la monotonía es creciente, en otro caso es decreciente, luego en x=-1 la función tiene un punto de mínimo. Como f(-1)= -1/e entonces el punto es (-1; 1/e).

• Signo: La función es positiva para x> 0 y negativa para x> 0

• La función no tiene paridad y el gráfico no tiene simetría

• Como f”(x)= (x+2)ex entonces x =-2 es un punto de inflexión y para x> -2 hay concavidad hacia arriba y en otro caso concavidad hacia abajo

• Asíntotas verticales no tiene, asíntotas oblicuas en +( no tiene porque 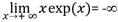. En -( se tiene que m= lim x→− ∞ exp (𝑥) = 0 y además

• n= lim 𝑥→− ∞ 𝑥 exp (𝑥) = 0, solo que este límite es resultado de resolver una indeterminación del tipo 0∙∞.

Del análisis de las propiedades anteriores resulta la imagen dada por: {y ∈𝑅; y≥− 1∕𝑒} . De todo esto resulta la gráfica que se muestra en la figura 2.

Fig. 2 Gráfica de la función f(x) = x exp(x) 

También antes de proceder a calcular la integral se consigue la interpretación geométrica de la integral para llegar a concluir que se trata de la región comprendida entre el eje de las abscisas y el gráfico de la función en el tercer cuadrante y tiene una relación con el área de la región. Se aprecia que es una región no acotada y la integral es impropia del tipo 1 (con intervalo infinito).

Se procede a calcular la integral y lo primero es resaltar que con este último método de cálculo se tiene una integral en la que para obtener su valor se aplican los dos métodos ya vistos:

En el cálculo de este límite hay nuevamente una forma indeterminada y del tipo 0 · (, y para resolver este problema se apela nuevamente a la regla de L´Hospital. Así, finalmente queda que, como era de esperar I = -1 y nuevamente el área de la región puede ser expresada por: A = /-1/ = 1 u2.

Se destaca lo siguiente: Dado que 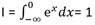y como las funciones reales f(x)=e^x y g(x)= lnx son inversas entonces las regiones geométricas asociadas a ellas son resultado de una reflexión en la recta y = x.

Se obtiene así un resultado interesante 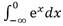=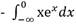. Más aún, se obtiene la generalización siguiente: 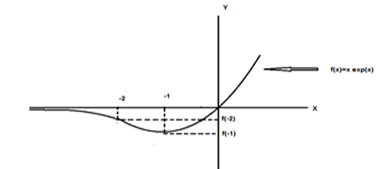. Esto permite el cálculo de algunas integrales sin necesidad de realizar los cálculos habituales de los métodos de integración.

En la figura siguiente se muestra el caso particular inicial.

Fig. 3 Gráficas de las funciones g(x) = exp (x) y f(x) = x exp (x) 

Problema 2: Piedra que se sumerge en un medio viscoso ^[14]

Una roca de masa m=3,00 kg cae desde el reposo en un medio viscoso. Sobre ella actúan una fuerza neta constante hacia abajo de módulo F1= 20,0 N (resultante de la gravedad y de la fuerza de flotación ejercida por el medio) y una fuerza de resistencia del fluido F2 = kv, donde v es la rapidez, medida en m/s y k=2,0 N s/m.

1. Calcular la aceleración inicial a0 de la roca

2. Calcular la aceleración cuando v = 3,00 m/s

3. Calcular v cuando a = 0,1 a0

4. Calcularla velocidad final vf

5. Calcular la posición, velocidad y aceleración 2 segundos después de iniciado el movimiento.

6. Calcular el tiempo necesario para que v = 0,9 vf

A nivel de aula para la realización de los cálculos se hace un diagrama de fuerzas como el que sigue y donde el signo se considera positivo hacia abajo

Fig. 4 Diagrama de fuerzas 

1. Como la roca parte del reposo entonces v = 0 m/s, por tanto, a0 =6,7 m/s2

2. Si v =3,00 m/s entonces 20-kv =3,0 a, entonces la aceleración a=4,67m/s2

3. Si a = 0,1 a0 entonces como a0 = 6,7 m/s2se obtiene que a =0,667 m/s2 y entonces de 20 - kv = 3,0 a resulta que v = 9,00 m/s

4. Para calcular vf se tiene en cuenta que con el aumento de la velocidad aumenta la fuerza de resistencia del fluido y llega el momento en que 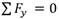y por lo tanto la aceleración se hace cero. Esto sucede si v = v_f, entonces de 20 - kv = 3,0 se obtiene que 20 - kv_f = 0. Por tanto v_f = 10,0 m/s

5. La posición, rapidez y aceleración, 2s después de iniciado el movimiento, se obtienen según la ecuación 20 - kv= 3,0a; se genera entonces 20 - kv = 3,0 dv/dt, ecuación diferencial cuya solución se construye según 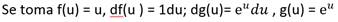. Si se integran ambos miembros resulta: 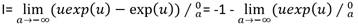. De donde 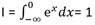. Esta expresión es consistente pues si 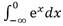entonces 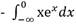y entonces 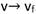. Al evaluar para t=2s se obtiene 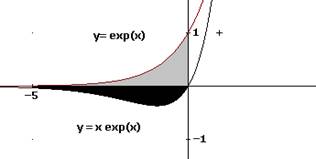, lo que determina la rapidez. En el cálculo de la coordenada se plantea que v = dy/dt y resulta que 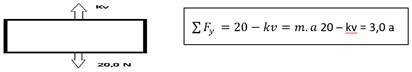y al integrar se obtiene 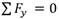; por lo tanto 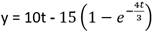y para t = 2s se obtiene que y= 8,95m. En determinar la aceleración se usa la expresión 20 - kv = 3,0 a y para el valor de v = 7,36 m/s se obtiene que a =1,76 m/s².

6. En el cálculo del tiempo necesario para que v = 0,9 v_f se considera 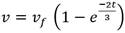y resulta 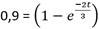de donde t = 3,45 s

Hasta aquí la solución del problema inicial planteado. Durante este proceso ha sido encontrado un conjunto de fórmulas que se relacionan entre sí. A este conjunto de fórmulas, entendido como sistema, en el contexto del problema planteado se le denomina modelo físico - matemático asociado al evento de la caída de una piedra en un medio viscoso y teóricamente está en correspondencia con las aplicaciones del modelado ^[8], ^[15].

Conviene recordar las expresiones analíticas del modelo, a saber, desde considerar F₁ como la resultante entre el peso del cuerpo y la fuerza de empuje del líquido se obtiene:

(1)

De la expresión (1) se deduce que:

(2)

Expresión calculable en cualquier lenguaje de programación. Si se requiere calcular v entonces se deduce, también de (1) que v = (F ₁ -ma)/k. En caso de ser necesario calcular la velocidad final v _f entonces esta se alcanza cuando a=0 y resulta v _f = F ₁ /k. Para obtener la expresión de v en función del tiempo se sustituye a por dv/dt en (2) y resulta dv/dt=(F ₁ -kv)/m de donde:

o sea

Integrando término a término

De lo que se deduce (3)

(3)

Modelo válido para cualquier valor de t y que desde su derivada da una expresión para la aceleración en función del tiempo, dada por: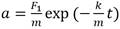

Desde (3) se obtiene una expresión para la ordenada y en función del tiempo dada por (4):

(4)

Las tres expresiones anteriores permiten obtener los valores de a(t), v(t) y y(t) en cualquier instante del proceso, pero también sugieren la idea de que se puede encontrar el instante del tiempo en que ocurriría un valor particular de alguno de ellos.

Para a(t), resulta 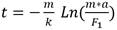y para v(t), resulta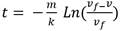

Para la expresión de la ordenada y no existe una fórmula analítica para el cálculo de la t correspondiente, aunque existen métodos numéricos que permiten calcularla, pero, más allá de esta posibilidad se puede plantear una nueva interrogante:

La masa m de la piedra es fácil de obtener pues basta deducir el peso desde la aceleración de la gravedad del lugar, la F ₁ es también fácil de obtener, basta pesar la piedra sumergida en el líquido viscoso, algo realizable con pocos recursos, pero, ¿cómo obtener k, coeficiente de resistencia a la velocidad en el medio viscoso? Para ello resulta necesario disponer de una instalación en la que se pueda medir esta fuerza a diferentes velocidades, posiblemente dejando fija la “piedra” y cambiando la velocidad del fluido.

Una instalación tan sencilla como el tanque en la que se suelta la piedra y con la posibilidad de medir la y correspondiente para determinados instantes de tiempo ofrece una opción para determinar k y también a F ₁ ; constituye una alternativa de laboratorio de bajo costo pero efectiva para experimentos sencillos y con su empleo se procede al cálculo de k y F ₁ a partir del modelo obtenido midiendo las 𝑦 para t=t ₁ , t=2t ₁ y t=3t ₁ .

Se sabe ya que 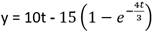. En lo que sigue se llama T a la variable definida por 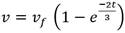. Lo que permite asegurar que de ser conocida T entonces se puede calcular k mediante (5)

(5)

Partiendo de la relación de los tiempos, como t2=2t1, ocurre entonces que 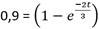y como t ₃ =3t ₁ resulta .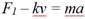

Las expresiones para y ₁ , y ₂ y y ₃ son las siguientes:

; ;

En las que las incógnitas son F ₁ y k, ya que m se considera conocida, los tiempos se asumen predeterminados y las y _i se miden para los tiempos correspondientes. Se debe puntualizar que t ₃ tiene que ser menor que el que demora la piedra en alcanzar la velocidad final v _f , para la validez del modelo, ya que para entonces T sería prácticamente cero.

Tras compleja manipulación algebraica se obtuvo el inesperado resultado que inspiró en gran parte el presente artículo:

Con el mismo se calcula k mediante la fórmula (5) y finalmente a F₁, según

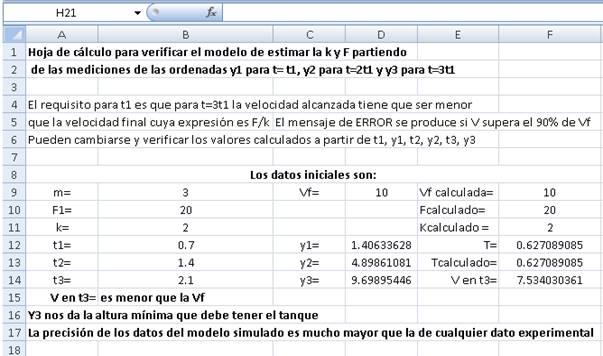
Las fórmulas se implementaron en una hoja de EXCEL y desde los valores de m, F ₁ y k, se calcularon las y para diferentes juegos de t ₁ y con ellos se recalcularon los valores de F ₁ y k comprobándose la coincidencia concebida. En esta hoja aparecen además casillas con los correspondientes valores de v y de a para los tiempos considerados. La hoja se establece como resultado de simular el experimento real y tiene el atributo de dar resultados más precisos que el experimento. A continuación, se muestra la hoja Excel.

Fig. 5 Hoja Excel para cálculos de k y F 

Consideraciones finales

La participación de los autores de forma activa durante años en todo el proceso de formación del ingeniero en metalurgia y materiales, y haber podido realizar acciones tales como evaluar o diseñar niveles organizativos del proceso docente educativo, controlar la marcha del proceso en el salón de clases y participar en la elaboración de otras propuestas didácticas anteriores similares es génesis histórica y epistemológica de la propuesta didáctica que se presenta.

En experiencias anteriores se participó en dos propuestas de problemas integradores, la primera en la asignatura Algebra Lineal y la segunda desde la asignatura Química - Física Metalúrgica desarrollada en la Universidad Metalúrgica de Moa Dr. Núñez Jiménez. La segunda aplicada a práctica laboral - investigativa. Infelizmente no generalizadas y perdidas en el tiempo. En esta tercera ocasión la propuesta deja agradables experiencias que marcan la diferencia con las versiones anteriores, a saber:

• Un acercamiento a la relación ciencia básica - ciencia de la ingeniería, en búsqueda de una interface ciencia - tecnología.

• La inclusión de una versión de laboratorio virtual con empleo de página Excel para registro de datos según modelo y simulación, y asociado a un experimento real, lo que permite un acercamiento a la formación profesional.

• Llevada al proceso docente en clases del tipo Clase Encuentro en la modalidad semi presencial de la misma carrera y posibilidad de ser integrada a la forma de enseñanza Seminario, esta última no realizada aún por los autores.

Dadas estas características de la propuesta los autores consideran que es oportuna la gestión por una generalización a otras asignaturas y contextos ingenieriles. La posible generalización en la carrera es el resultado hacia el cual se requiere llegar como solución del problema y hacia donde intentan acercarse los autores con la propuesta.

Conclusiones

1. Se ha descrito una propuesta didáctica basada en el planteamiento de problemas en cuyos procesos de construcción de las respectivas soluciones se sistematizan conocimientos y procedimientos de cálculo propios de la enseñanza en la ingeniería, y se identifican resultados nuevos sencillos no conocidos por los estudiantes.

2. Se desarrolla un modelo físico - matemático para modelar la caída de un cuerpo y su inmersión en un líquido dado en el contexto de la solución de un problema de la mecánica de los fluidos, rama harto presente en la ingeniería, cuya implementación en auxiliares matemáticos facilitó y estimuló el trabajo de los alumnos y el trabajar con experimentos realizables a escala de laboratorio docente en el que se logra medir magnitudes (tiempo y longitud) de manera aceptable amplió las perspectivas del uso que puede dársele a una instalación sin grandes gastos.

3. Con la propuesta se genera un acercamiento a un mayor y mejor tratamiento de los problemas en toda la carrera y además se da un paso en la relación ciencia básica - ciencia de la ingeniería como interface para llegar a igual propósito en el diseño de las tecnologías.

Referencias bibliográficas

1.  Soto E. Un acercamiento a la didáctica general como ciencia y su significación en el buen desenvolvimiento de la clase. Atenas. 2012; 3(20):1-18.

2.  Arcavi A. Problem - driven research in mathematics education. Journal of Mathematical Behavior, 1988 19: 141-173.

3.  Labarrere A. Solución de problemas, construcción de objetos matemáticos, y desarrollo del pensamiento del estudiante. RECHIEM. 2006; 2: 44-60.

4.  Soloviova Y. Las aportaciones de la teoría de la actividad para la enseñanza. Educando para educar. 2019; 20(37): 13-24.

5.  Puig L. Presencia y ausencia de la resolución de problemas en la investigación y el currículo. Actas del XII Simposio de la Sociedad Española de Investigación en Educación Matemática. 2008: 1-18.

6.  Asensi V y Parra A. El método de la ciencia y la nueva filosofía de la ciencia. Revista Análisis de documentación. 2002; 5: 9 -19.

7.  Artigue M. La educación matemática como un campo de investigación y como un campo de práctica: Resultados, desafíos. XIII Conferencia Interamericana de Educación Matemática. 2014: 43-59.

8.  Sharhorodska O, Padrón A y Bedregal N. Las matemáticas y la formación del ingeniero, como una relación simbiótica. Referencia Pedagógica CREA. 2018; 6(2):175 - 189.

9.  Paz I y Padrón A. La transformación curricular por competencias: una propuesta desde la integración y participación de los docentes. Referencia Pedagógica CREA. 2020; 8(2):235-250.

10.  De la Peña G, Velázquez RM. Algunas reflexiones sobre la teoría general de los sistemas y el enfoque sistémico en las investigaciones científicas. Revista cubana de Educación superior. 2018; 37(2).

11.  Faustino A, Wongo E y Craib A. El enfoque dialéctico en la formación matemática y su repercusión científico -tecnológica en el contexto social. Prisma Social. 2015; 14:574-602.

12.  Stewart J. Cálculo. Trascendentes tempranas. 4ta ed. Thomson Editores. México 2002.

13.  Tupacyupanqui D y Padrón A. Rediseño curricular de la asignatura Cálculo en una variable para ingeniería en sistema. Referencia Pedagógica CREA. 2019; 7(1):121-138.

14.  Otero L. Fenómenos de transporte en Metalurgia Extractiva, España, Editorial Alhambra S.A., 1986:830 p.

15.  Niss M, et al. Modelling and applications in mathematics education. 14 th ICMI Study. 2007: 3 -32

Recibido: 09 de Febrero de 2021; Aprobado: 22 de Abril de 2021

^*Autor para correspondencia: [e-mail]

La concepción del trabajo científico fue realizada por Leandro López Rubira e Isora María Arcia Rivero. La recolección, interpretación y análisis de datos estuvo a cargo de los tres coautores en partes equivalentes. La redacción y edición del documento fue realizada por Lierli Oconnor Montero. La revisión final y aprobación del documento fue realizada por los tres coautores.

Los autores declaran que no existe conflicto de intereses

Leandro López Rubira. Ingeniero. Asistente. Facultad Ingeniería Mecánica. Departamento de Metalurgia. Universidad Tecnológica de La Habana “José Antonio Echeverría”, Cujae. La Habana, Cuba

Lierli Oconnor Montero. Doctor en Ciencias Pedagógicas. Profesor Titular. Facultad de Ingeniería Mecánica. Departamento de Metalurgia. Universidad Tecnológica de La Habana “José Antonio Echeverría”, Cujae La Habana, Cuba

Isora María Arcia Rivero. Ingeniera. Instructor. Centro de Investigación para la Industria Minero Metalúrgica. La Habana, Cuba