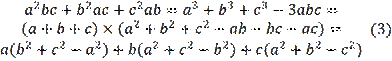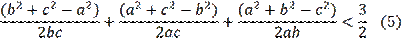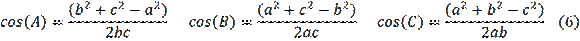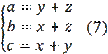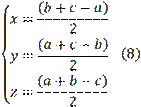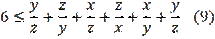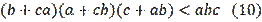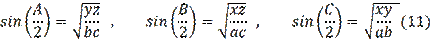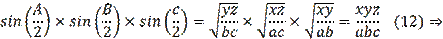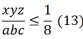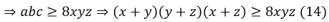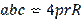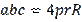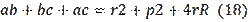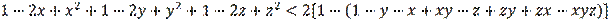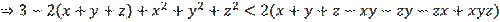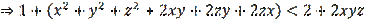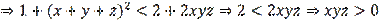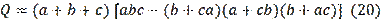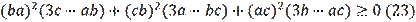Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introduction
Geometry is the branch of mathematics concerned with the shape of individual objects, spatial relationships among various objects, and the properties of surrounding space. It is one of the oldest branches of mathematics, having arisen in response to such practical problems as those found in surveying. In fact, its etymological roots are derived from Greek words meaning “Earth measurement”. However, over time, the scope of geometry extended beyond the investigation of flat surfaces (commonly referred to as plane geometry) and rigid three-dimensional structures (known as solid geometry). Instead, it was acknowledged that even the most abstract concepts and mental representations could be expressed and developed through geometric principles (Heilbron, 2023). Thus, today there are various branches of geometry including differential geometry, algebraic geometry, and geometric analysis which are characterized by the objects they study and the methods that are used in this purpose.
As pointed out by Dillon (2018) many mathematicians who specialize in geometry do not talk about similar triangles or alternate interior angles or angles in a circle or most of the other things people think about school geometry, that is, Euclidean geometry. But as in many other fields of science, knowledge is built on the basis of previous discoveries, from the simple to the complex, and although sometimes dismissed by students, the study of geometry and its demonstrations has a profound impact. For example, the utilization of demonstrations can serve as a means to elucidate the points of convergence between mathematical knowledge and personal experience within the practice of "engaging in mathematics." This approach facilitates the amalgamation of one's cognitive awareness, rendering the underlying purpose more transparent, dissecting the entirety into constituent components, transforming the implicit into the explicit, and advancing incrementally through the various stages of problem-solving (Barra et al. 2009; Ingram, 2021).
Within geometry, a triangle represents a fundamental, characterized as a polygon possessing three sides, thereby constituting a closed, two-dimensional figure composed of straight segments. Within the domain of geometry, triangles hold a distinctive status owing to several inherent properties: 1) the sum of the internal angles of any triangle invariably totals 180 degrees, 2) in a triangle, the length of each side is invariably less than the sum of the remaining two sides, a principle known as the triangle inequality. Triangles can be categorized based on two primary criteria: the lengths of their sides and the magnitudes of their angles. This classification gives rise to several distinct types of triangles, including equilateral, isosceles, scalene, acute, right, and obtuse triangles. The application of triangles extends across diverse fields such as mathematics, engineering, and architecture, where they find relevance in addressing a wide array of real-world problems and calculations. In fact, Clark and Pathania (2023) include triangle congruence as one of the foundational principles of Euclidean geometry.
Considering the above, the objective of this work is to discuss some open questions in the equivalence of certain statements in triangles. We would like to point out that the cases analyzed show considerable complexity, however these types of open problems are found more frequently in practical activities, so a school mathematics course should help students develop the ability to solve them.
Materials and methods
The main method used is direct demonstration. The method of direct demonstration, grounded in axiomatic principles, constitutes a means of establishing the validity or invalidity of mathematical propositions through the logical integration of established facts, typically rooted in axioms. Axioms are foundational truths within a given mathematical system that necessitate no further proof, serving as the bedrock upon which all subsequent theorems are constructed. Then, a direct proof represents a systematic and logical progression of statements designed to demonstrate the veracity or falsity of a given assertion. This method harnesses a concatenation of simple statements, commencing with the hypothesis and culminating in the desired conclusion, while making use of axioms, definitions, postulates, theorems, and lemmas.
Direct proof is recognized as the most elementary form of mathematical proof and is meticulously assembled by orchestrating a series of logical steps, wherein the conclusion is ultimately underpinned by the harmonious synthesis of axioms, definitions, and previously established theorems. Consequently, direct demonstration, founded upon axiomatic principles, stands as a pivotal and fundamental technique for substantiating mathematical statements.
Results and discussion
Proving the equivalence of certain statements has always been highly appreciated not only in school mathematics, but throughout the scientific world. These proofs are considered more valuable when the proven (equivalent) statements have different structures. It is clear that the equivalence of different statements, generally speaking, is proved in different ways. And if several different statements are proved in the same way, this is considered very effective. In this work, the equivalence of some different statements from the topic of triangles is proved in the same way.
Recently, I accidentally saw one small note by (Chernikov, 2003, p.43) where the equivalence of the following two problems is proved:
Problem 1. Let us denote by 
the lengths of the sides of a certain triangle. Let's prove that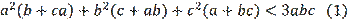 
.
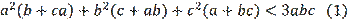Problem 2. Prove that for angles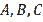 
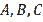of any triangle the following inequality is true: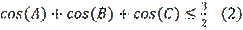 
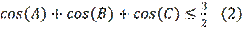. (Morozova & Petrakova, 1971).
As can be seen, these tasks have different structures. To prove these problems, the author uses the following method. Let’s assume that problem 2 has been solved. We must prove (1) using (2). Notice, that:
Then inequality (1) is reduced to the form:
So, we need to prove that:
Using the cosine theorem from (5) we obtain (2). On the contrary, let us assume that Problem 1 has been solved. By the cosine theorem, we have:
Then, considering the equalities in (4) we got (2). These problems and their solutions require some creativity. But, nevertheless, guessing equality (3) is almost random by nature and it is checked by direct calculation by opening the brackets. Notice that the solution is based precisely on inequality (3). Then, what happens if we fail to find equality (3)? In this regard is important to point out that there are quite a few such problems among the Olympiad problems. What to do then? How to find a universal, constructive method for solving a given problem? This topic in geometry is quite large, rich, and full of variety, as well as Olympiad problems.
In the book by Prasolov (1986) the author talked about just one such technique, the initial basis of which is the problem 15.9 from (Lyapin et al. 1973).
Problem 3. Let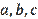 
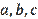be given numbers. Prove that the existence of positive numbers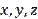 
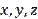for which the equalities hold:
Is a necessary and sufficient condition that the numbers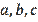
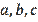be the lengths of the sides of some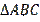 
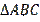. Lyapin et al. 1973, proposed the following solution from system (1). By simple calculation we find that:
System (7) is also easily obtained from (8), i.e., systems (7) and (8) are equivalent. Indeed, let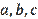
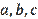be the lengths of the sides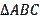 
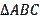. Then, using the triangle inequality, we can state that from (8) the numbers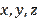 
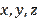found will be positive. On the contrary, if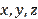 
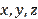are positive numbers, then from system (7) the found numbers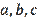 
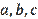will be positive and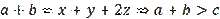 
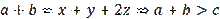and also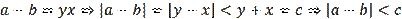 
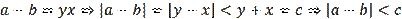etc. That is, the numbers
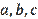satisfy the triangle inequality and they can be the lengths of the sides of some triangle.
Thus, knowing the values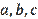
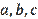from (8), we find new values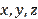
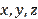. How do these two systems of numbers differ and what benefit do new values of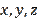 
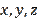bring when solving (or proving) similar problems as Problem 1 and Problem 2 and for what reason does this effect occur? Our answer is:
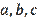
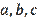are the lengths of the sides of a certain triangle, which means they are positive and satisfy the triangle inequalities. This means that when we solve some problem on the topic of triangles, and we must take this fact into account in all reasoning in solving this problem. In this sense, this fact plays the role of an additional load on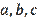
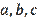because these quantities are not free.
On the contrary, the quantities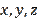
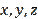are also positive, but unlike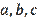
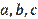, they do not have to satisfy the triangle inequalities (this is the main difference from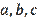
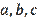). Let's check this in a specific example. Let’s build a triangle with data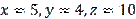 
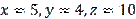. The sum is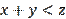 
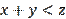(not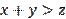 
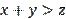as expected). Using these data from (1), we find the lengths of the sides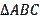
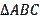which need to construct: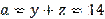 
, 
, 
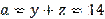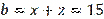
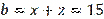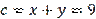
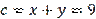. And as can be seen the numbers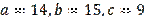 
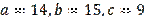can become side lengths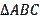
.
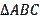Let us explain the reason for this phenomenon. From (8), for example,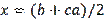 
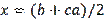. Here we see the difference between the sum of two sides and the third side. It is known that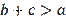 
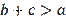, but to what extent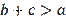
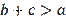, there is no upper limit on this. This means that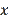 
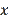, as well as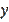 
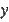and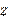 
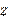, are independent of each other and can take on any positive value. In other words, unlike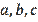
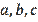, the variables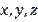 
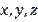are free and can take on any positive value independently of each other. Therefore, we can expect that the variables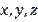
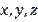have greater capabilities in solving problems than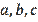
.
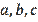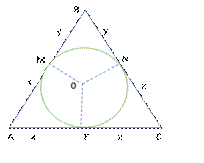
The quantities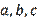 
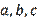and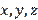 
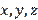connect two important figures of planimetry like a triangle and a circle (Figure 1). In the figure MNP are the tangent points,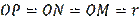 
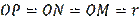are the radius of the inscribed circle, and 
, 
, 
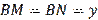
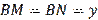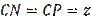
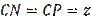. Then, from Figure 1 it is easy to obtain equalities (7).
Based on the above about the system of quantities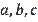 
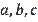and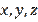 
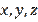and Figure. 1 Lyapin et al. (1973) put forward the following idea: “if a problem on the topic triangles is presented in the language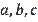
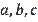, it is first translated into the language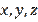
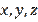using equalities (7)” and some necessary formulas with the hope that they received a more effective solution. Then, the authors provided a complete list of basic formulas in the language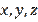
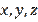(with proof). Some formulas used in mixed language for convenience. We will use them here as needed related to a specific task. Let's return then to problems 1 and 2.
First, let us note one important point: Chernikov (2003) proved the equivalence of inequalities (1) and (2), but the validity of these inequalities remains open. Let us recall that in proving the equivalence of inequalities (1) and (2), Chernikov (2003) used equality (3), which raised some questions for us. Let's try to translate inequality (1) into the language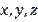
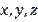using equalities (7). Inequality (1) then takes the form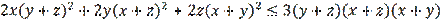 
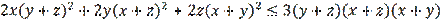. By simple calculation and simplification, we can easily verify that inequality (1) leads to true inequalities of the form of (9)
Considering that x, y, z are positive numbers, the validity of inequality (9) is beyond doubt. For inequality (2), first from Lyapin et al. (1973) we produce the following formulas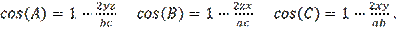 
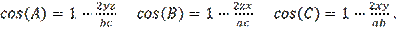Then inequality (2) takes the following form: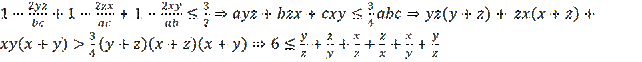 
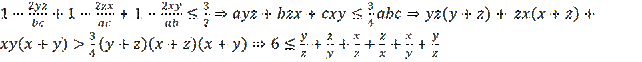
And here this inequality is verified by ordinary calculation. The equivalence of inequalities (1) and (2) is obvious, since both of them, using the quantities
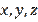, are reduced to the same inequality (9). Since (9) is a true inequality, we also prove the validity of inequalities (1) and (2) (this proof is not given by Chernikov (2003) in the language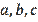
).
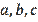Identifying the equivalence of problems, especially when they have different structures, has great practical value. We often observe the equivalence of Olympiad and competitive problems in different books. Discovering the equivalence of a series of problems in time certainly has a positive effect on the content and structure of the books written. In one specific example, we saw that switching to language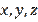
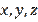does not help us with this. Let's give one more example. İt is proposed to prove the inequality (10) where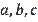
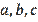are the lengths of the sides of some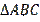
.
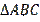Note that the circumscribed circle is equivalent. To prove these three inequalities, we need the following proven formulas from Lyapin et al., (1973):
In these formulas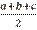 
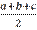is the semiperimeter of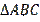
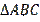, then:
It follows that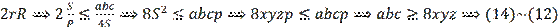 
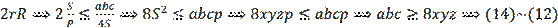. This means that all three inequalities (12-14) are equivalent to each other.
How many more equivalent problems there are in published works is a big question. In addition to proving the equivalence of statements, the variables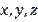
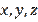can be effectively used in other problems, as well as in proving some theorems of planimetry. In Lyapin et al. (1973) about 20 main types of problems were selected from the topic of triangles.
An example is next, let the perimeter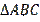
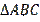be constant number, P=O. In what case does this triangle have a maximum area and find the value of this area. The solution is when the semi-perimeter: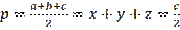 
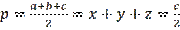. According to the formula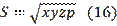 
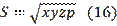where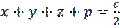 
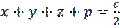is a constant number. Then, the product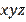 
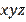has a maximum value when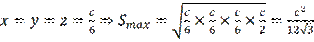 
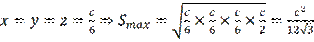and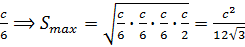
. And, if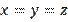 
then from (7) it follows that a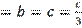
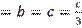, i.e.,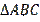
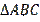is equilateral with side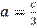 
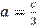and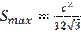 
.
It often happens that the proposed problem on the topic of a triangle is difficult to solve in the language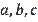
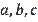. Either it is difficult to choose a solution method, or it is necessary to prove some preliminary statements. These difficulties are probably because the quantities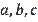
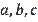satisfy the triangle inequalities. In such cases, they often switch to language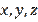
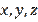and this transition basically justifies itself, because they are free variables (positive). Let's analyze another example.
Problem 4. In triangle ABC, prove the inequality (17) if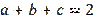 
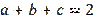, where
are the lengths of the sides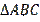
.
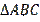In the solution, the author proposes to first prove the following preliminary equalities (18) from (1) where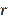 
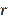and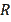 
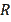are the radii of the inscribed and circumscribed circle, respectively.
; 
The further part of this solution is naturally connected with these unexpected equalities. This constitutes additional difficulties, and these difficulties are also mysterious, since the need for equalities (18) in the solution is unfounded from the very beginning of the solution. Other similar questions rise here but one thing is clear - this solution cannot be considered the most effective solution. What happens if we fail to guess the equalities in (18)?
If we move to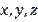
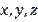, we will immediately notice that from the additional condition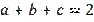 
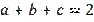it follows that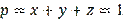 
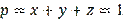. Hence,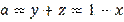 
, 
, 
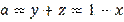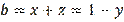
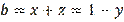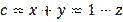
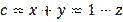and inequality (17) will take the form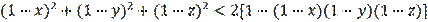 
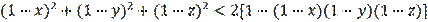. When simplifying this inequality, we will take into account that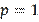 
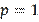as shown next:
We have obtained a correct inequality, which means that inequality (17) with the condition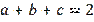 
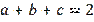is also true. Here it is considered that during the calculation we made equivalent transformations. We wonder where equalities (18) that were necessary to solve this problem disappeared? Let’s look at another example.
Problem 5 (XLV Moscow Olympiad, 1982). Prove that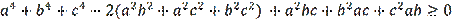 
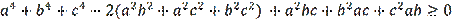(19).
If we denote the left side of this inequality by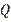 
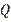, then by direct calculation we will arrive at (20).
After this, based on inequality (10), inequality (19) is obvious.” But again the same question: how to find (20)? What will we do if we fail to guess this identity? Moving to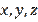
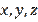(19) is proved without (20) [see problems 5-9 in Lyapin et al.(1973)].
On the other hand, the nature of the variables x, y, z sometimes makes it possible to apply the methods of higher mathematics to solving some problems from school mathematics as in the next example.
Problem 6 (XXIV Olympiad, Moldova, 1980). When in triangle ABC the condition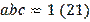 
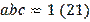is satisfied. Find the maximum area of this triangle if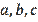
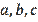are the lengths of the sides of this triangle.
If we switch to the language,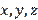
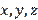we must find the maximum of the function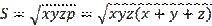 
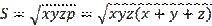considering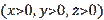 
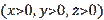provided that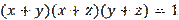 
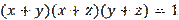. Further, the solution is completed using the conditional extremum method [see task 18.9 in Lyapin et al., (1973)].
In addition, sometimes you have to make the reverse transition, i.e., if the problem given in the language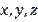
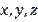these are arbitrary positive quantities. If we use formulas in (8) we switch to the language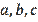
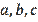and obtain the corresponding equivalent problem on the topic of triangles. The resulting statement does not require additional proof. An example is shown in the next problem.
Problem 7. Proof that for any positive variables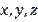
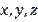the following inequality is true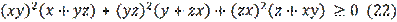 
.
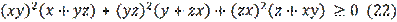By finding the corresponding equivalent problem in language
on the topic of triangles we arrive at (23).
Inequality (23) is complex, and it will probably not be easy to prove this inequality without (22). We encourage the reader to take it on as a challenge.
Conclusions
The proof of equivalent problems in the geometry of triangles plays an essential role in the field of mathematics and has profound relevance both in mathematical theory and in its practical applicability. In our opinion, the proof of equivalent problems in the geometry of triangles is essential to establish a solid foundation in mathematics since the methods of proof encourage critical thinking and the ability to reason logically. Those involved in proving equivalent problems develop analytical skills that are valuable not only in mathematics, but also in a wide range of academic and professional disciplines. In terms of practical applicability these demonstrations have direct relevance in engineering, physics, architecture, cartography, and many other areas. Throughout this work, various aspects of this area have been explored, highlighting the challenges involved in its analysis. Considering everything that was discussed, we can say that the question we raise is serious in nature. How many other equivalent problems exist in published works? How to find them all?
