Vicerrectoría de Investigación. Instituto Superior
de Ciencias Médicas de La Habana

Análisis espacial de la mortalidad en áreas geográficas pequeñas. El enfoque bayesiano*

Luis Carlos Silva Ayçaguer,1 Alina Benavides Rodríguez2 y Carmen Lucía Vidal Rodeiro3

Resumen

El empleo de mapas para representar algunas realidades y acontecimientos relevantes en materia de salud, proporciona probablemente una imagen más expresiva de su distribución espacial que la simple observación de datos en tablas. Mediante los mapas se puede conocer el patrón de distribución geográfica de estos sucesos, y sugerir posibles explicaciones sobre las distribuciones identificadas. Consecuentemente, la construcción y suavizado de mapas han sido objeto de recientes desarrollos metodológicos. El enfoque tradicional ha consistido en representar en los mapas las razones estandarizadas de mortalidad (REM); sin embargo, cuando el número de casos en espacios geográficos reducidos es bajo, las tasas brutas de mortalidad son muy lábiles, y su representación a través de un mapa exhibe una variación amplia y poco informativa de los patrones existentes. Los métodos bayesianos ofrecen la posibilidad de “corregir” estos mapas, para que emerjan directamente patrones que no serían visibles cuando se emplean procedimientos estadísticos clásicos. Para ilustrar y explicar más detalladamente ambos métodos se utilizaron los datos de mortalidad por accidentes en Cuba, del año 1998. Para este análisis se dividió a la población en 7 grupos de edad: 0 a 14, 15 a 24, 25 a 34, 35 a 44, 45 a 54, 55 a 64, y 65 o más años; en calidad de áreas geográficas se consideraron los 169 municipios del país. Se muestran dos mapas: uno confeccionado según los métodos tradicionales, y otro según los métodos bayesianos. En este último se observa claramente el efecto de la suavización; el patrón espacial de la mortalidad, antes difuso, permite apreciar que la mortalidad por accidentes es especialmente acusada en los municipios más desarrollados.

DeCS: DISTRIBUCION ESPACIAL/estadísticas y datos numéricos; SALUD; MAPAS; UBICACIONES GEOGRAFICAS; MORTALIDAD; TEOREMA DE BAYES; DENSIDAD DE POBLACION; CUBA.

Introducción

La representación mediante mapas, de ciertos acontecimientos de salud relevantes (como la distribución de la mortalidad) proporciona, en algunos casos, una imagen más elocuente de su configuración espacial, que la mera observación de datos organizados en tablas. Tal perspectiva aporta, como mínimo, una apreciación complementaria para las representaciones clásicas, ya que pueden manifestarse patrones expresivos de ordenamiento geográfico de esos sucesos. Si bien los estudios asociados a este enfoque pueden verse afectados por el llamado sesgo ecológico,1 es imprescindible comprender que no siempre se quiere “trasladar” las conclusiones propias del ámbito grupal al individual, en cuyo caso el sesgo no es motivo de preocupación. Por otra parte, las ventajas de su desarrollo son obvias: tienen bajo costo y permiten responder preguntas relacionadas con el ambiente muy difíciles de encarar por otros medios.2-4

En su vertiente descriptiva, este tipo de análisis permite detectar la existencia de agrupaciones espaciales, y contribuye a cuantificar en términos absolutos y relativos la importancia de las diferencias presentes en un territorio5 (típicamente un país). Es muy útil para la vigilancia de las enfermedades crónicas.6 En la vertiente exploratoria, ayuda a sugerir posibles explicaciones para las distribuciones identificadas. En efecto, el estudio de la variación del riesgo en el espacio para cierta causa de muerte puede permitir la formulación de hipótesis acerca de sus determinantes, y revelar indicios para orientar futuros estudios de investigación que procuren explicaciones más refinadas.7

Se conoce, sin embargo, que cuando los indicadores se miden sobre espacios geográficos reducidos, especialmente si, además, el número de casos (numerador) es pequeño, las tasas brutas de mortalidad o morbilidad son muy “lábiles”, y su representación a través de un mapa exhibe una variación amplia y poco indicativa de los patrones vigentes.8

El enfoque tradicional para conjurar este problema ha consistido en representar en los mapas las razones estandarizadas de mortalidad (REM). Sin embargo, cuando estas se calculan para áreas en las cuales los casos observados y esperados son escasos, ha sido porque el desenlace de interés es “raro”, las áreas sobre las que se trabaja son pequeñas, o incluso, por ambas circunstancias. También se suelen producir estimaciones del riesgo relativo muy extremas (muy bajas o muy altas en relación con las demás) que van ubicándose de manera caótica en el mapa hasta el punto de obstaculizar una interpretación epidemiológica sugerente, útil.

Los métodos bayesianos ofrecen la posibilidad de “corregir” estos mapas, y por la estabilidad que alcanzan los estimadores, propician que emerjan estructuras que no pueden apreciarse directamente con los procedimientos estadísticos clásicos. Por eso numerosos investigadores aplican las técnicas bayesianas para estimar y “mapificar” las tasas de mortalidad según el área geográfica.9 Como fundamenta Breslow,10 esos enfoques parecen ser particularmente útiles para esta tarea, porque pueden incorporar la estimación interna de los efectos de la edad sobre las tasas, y bajo la misma formulación, contemplar la correlación espacial que suelen exhibir entre sí las diferentes áreas -por ejemplo, es lógico esperar que la mortalidad en cierta unidad territorial, sea más parecida a la de una contigua, que a la de una distante.

En este trabajo se repasan los métodos tradicionales y se bosquejan los recursos bayesianos para el análisis en áreas geográficas pequeñas, lo cual se ilustra mediante un ejemplo en el que se aplican ambos procedimientos.

Métodos tradicionales

Como se sabe, las tablas que contienen tasas por grupos de edad y sexo no se interpretan fácilmente por la gran cantidad de datos que suelen contener; esto explica la necesidad de buscar recursos expresivos más sencillos, que ayuden en la toma de decisiones.

Para simplificar la discusión, en lo sucesivo consideraremos que tenemos unidades territoriales en que se puede desagregar un espacio dado (por ejemplo, un país) y que estamos analizando la mortalidad por cierta causa. El examen de las tasas brutas de estas unidades puede llevar a conclusiones erróneas, puesto que las diferencias entre poblaciones pudieran ser imputables no solo a la intensidad del fenómeno, sino a confusores entre los cuales el más clásico es la estructura por edad, que puede diferir sensiblemente de una unidad a otra. Por otra parte, operar con tasas específicas por grupos de edad, es una alternativa para contemplar esta realidad que no permite un juicio sintético, ya que si, por ejemplo, se cotejan dos unidades, tendrían que establecerse comparaciones entre tantos pares de valores como grupos de edad se consideren, y las diferencias entre los valores de cada par podrían ser de distinta magnitud y signo. De modo que, con el objetivo de neutralizar el efecto de las distintas composiciones por edad en el cálculo de las tasas brutas, con frecuencia se acude al ajuste de tasas por edad para cada unidad territorial considerada. Con ese propósito se pueden utilizar dos métodos bien conocidos:11

• Ajuste directo: Consiste en aplicar las tasas específicas de mortalidad de las poblaciones estudiadas a una misma población hipotética denominada población estándar.
  
• Ajuste indirecto: Compara el número observado de muertes en cada unidad con el número esperado que se obtiene al aplicar las tasas específicas de una población de referencia (por ejemplo, la de todo el país) a la estructura de edad de cada una de las unidades territoriales.12 La razón entre estos dos números (observado y esperado) es lo que se conoce como razón estandarizada de mortalidad (REM).

Entre estas dos variantes, con frecuencia se prefieren las REM, en buena medida porque consienten una interpretación ágil y sencilla: por ejemplo, una REM mayor que uno para una unidad geográfica dada significa que la mortalidad para esa unidad es mayor que la que le correspondería, si su patrón de mortalidad fuese similar al de la población de referencia.

Sin embargo, este método ha sido a su vez cuestionado debido a que las REM pueden resultar notablemente dependientes de los tamaños poblacionales, lo cual implica el impacto sobre la variabilidad de las estimaciones, fenómeno que ocurre con más frecuencia cuando las unidades geográficas sobre las que se quieren representar las tasas son pequeñas.8 Dicho de otro modo: cuando los datos son son escasos, se pueden producir estimaciones inestables para las REM en cada área: típicamente, las estimaciones extremas tienden a ubicarse en aquellas áreas cuyos tamaños poblacionales son más pequeños; puede ocurrir, por ejemplo, que una REM alta en cierta unidad no necesariamente responda a la presencia de una verdadera singularidad en ese sitio, sino más bien por simple azar, que se expresa gracias a la reducida magnitud de los valores involucrados en su cómputo.

Para ilustrar y explicar más detalladamente estas ideas, consideraremos los datos de mortalidad por accidentes en Cuba, del año 1998. En calidad de áreas geográficas se tomarán los 169 municipios en que se subdivide el país. La información relacionada con las defunciones se obtuvo de la Dirección Nacional de Estadística del Ministerio de Salud Pública y los datos relacionados con la distribución de la población por edades en 1998, fueron proveídos por la Oficina Nacional de Estadística. Para el análisis se consideraron 7 grupos de edad: 0 a 14, 15 a 24, 25 a 34, 35 a 44, 45 a 54, 55 a 64 y, finalmente, 65 y más años.

Para cada municipio la REM tiene la siguiente expresión:

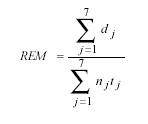
donde dj denota el número de defunciones observadas en el j-ésimo grupo de edad, nj es el total de personas-año (equivalente al número de personas cuando se opera con un solo año), y tj representa la tasa de mortalidad de Cuba en cada grupo de edad donde Cj ess el número de defunciones en el grupo de edad j-ésimo para todo el país y Nj el total poblacional en ese grupo); njtj expresa el número esperado de muertes en el j-ésimo grupo de edad. Veamos cómo se realizan estos cálculos a través de un ejemplo. Consideremos el municipio Mantua de la provincia más occidental de Cuba, Pinar del Río. La información necesaria para el cálculo de las REM se resume en la tabla.

TABLA. Datos poblacionales y de mortalidad por accidentes en 1998, en el municipio Mantua y en Cuba por grupos de edad

Grupo de edad ( j )	Defunciones en Mantua (dj)	Población de Mantua (nj)	Total de defunciones en Cuba (Cj)	Población total en Cuba (Nj)
0 - 14	1	6 217	345	2 417 901
15 - 24	1	4 026	462	1 531 972
25 - 34	2	5 434	709	2 216 736
35 - 44	1	3 715	506	1 619 490
45 - 54	1	2 946	421	1 308 615
55 - 64	2	2 946	424	951 361
65 y más	4	2 055	2 430	1 093 800

Las defunciones observadas en Mantua aparecen en la segunda columna; se aprecia, por ejemplo, que en el grupo de edad de 0 a 14 años se produjo una sola muerte por accidente durante el año 1998. La suma de esa columna constituye el numerador de la REM:

Como vimos anteriormente, el denominador de la REM es el total de casos esperados. Para calcularlo se divide el total de defunciones de cada grupo de edad (Cj) entre la población total de ese grupo (Nj) y se multiplica el resultado por la población de Mantua del grupo de edad correspondiente. El valor esperado de muertes en el municipio es la suma de esos productos para todos los grupos de edad:

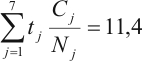
Consecuentemente, el valor de la REM para Mantua es igual a 1,05 (resultado de dividir 12 entre 11,4).

La figura 1 muestra la representación de las REM por accidentes (1998) para los 169 municipios cubanos. Desde el punto de vista matemático, la REM es un valor que se ubica de manera natural alrededor de 1; para que sus valores se visualicen más fácilmente en este ejemplo, se representan categorizadas según su distribución por quintiles. Las REM se clasifican, entonces, de acuerdo con los intervalos siguientes: 0 a 0,7716; 0,7717 a 0,8842; 0,8843 a 1,0297; 1,0298 a 1,1804 y 1,1805 a 1,7892. Obsérvese que tal agrupación conforma grupos con tamaños bastante homogéneos (3 con 34 municipios, 1 con 33 y 1 con 35). Gráficamente, se representan en cinco tonalidades.

Como se puede apreciar en la figura 1, es difícil discernir los patrones de mortalidad, hecho que se debe a la presencia de valores extremos, quizás ocasionados por fluctuaciones aleatorias no estructurales, que tienen un impacto engañoso en las áreas más pequeñas. Para esclarecer más lo que se quiere expresar cuando se afirma que las tasas son “lábiles” en las áreas más pequeñas, profundicemos en el ejemplo. Al observar que el municipio Mantua (en el extremo occidental y al norte de la isla) exhibe un tono oscuro, podríamos pensar que es una zona de elevado riesgo, muy diferente al de sus municipios vecinos. Sin embargo, adviértase que, por ejemplo, en el grupo de 55 a 64 años, la tasa de mortalidad asciende a 10,0, un número mucho mayor que el correspondiente a toda Cuba para ese grupo de edad (que ascendió a 4,5). Pero resulta que tan alarmante cifra se debe a solo 2 defunciones. Si se hubiera producido solo una muerte en ese grupo (quizás debido a un hecho tan coyuntural como que la víctima de un accidente de tránsito pudo sobrevivir ya que por casualidad pasó una ambulancia por la zona del accidente cuando éste se produjo), entonces la tasa específica se reduciría a la mitad, la frecuencia observada sería igual a 11 y la REM pasaría a ser 0,96. A la representación de Mantua en el mapa le hubiera correspondido, en ese caso, un tono más claro.

FIG. 1. Representación espacial de la razón estandarizada de mortalidad por accidentes, para todos los municipios de Cuba, año 1998.
Escala 1: 1 000 000

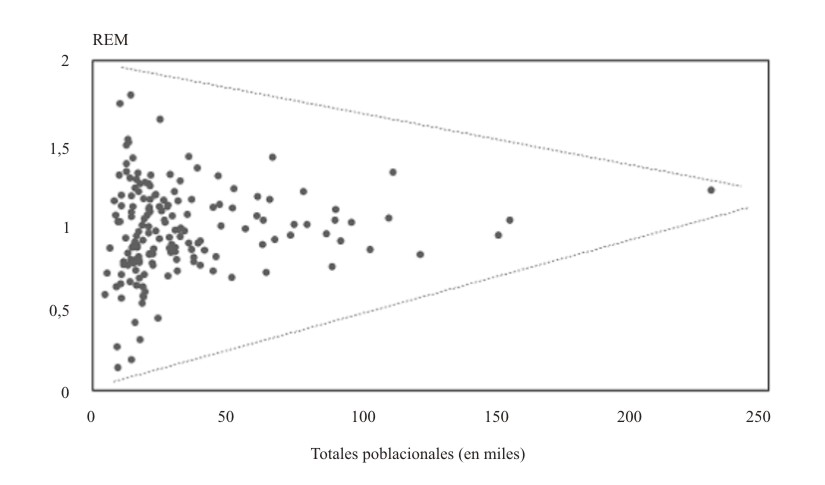
Como suele ocurrir, los valores más extremos de las REM tienden típicamente a producirse en las áreas de menor tamaño. En la figura 2 se han ubicado los puntos cuyas abscisas son los tamaños poblacionales de los 169 municipios cubanos, y cuyas ordenadas son las REM correspondientes. Obsérvese cómo la dispersión disminuye a medida que aumentan los tamaños poblacionales (las líneas de punto se han colocado para subrayarlo), hecho coherente con el supuesto de que las tasas estandarizadas son mucho más “inestables” cuando se computan sobre áreas pequeñas.

 

FIG. 2. Diagrama de dispersión de las REM por accidentes en 1998, y los totales poblaciones para los 169 municipios de Cuba.

 

Para solucionar este problema (eliminar o mitigar el efecto distorsionado de fluctuaciones aleatorias) una posibilidad consiste en calcular las “REM suavizadas” mediante un modelo jerárquico bayesiano.

Métodos bayesianos

En primer lugar, recordemos la esencia del enfoque bayesiano. A diferencia de los métodos estadísticos tradicionales, este enfoque no se reduce a operar con la información empíricamente conseguida sino que la combina con los criterios a priori que posee el investigador, nacidos tanto de estudios previos como de reflexiones racionales y juicios razonablemente conformados. Como resultado de tal integración, que se realiza por conducto del teorema de Bayes, se obtiene una llamada visión a posteriori que constituye la base de las inferencias subsiguientes.13

En el marco que nos ocupa, el enfoque bayesiano opera con dos tipos de información relevantes para la estimación de las tasas de mortalidad o morbilidad en un área determinada. El primero viene dado por el monto de personas-tiempo considerado en una determinada área geográfica, y el segundo es el número de defunciones o casos observados de la enfermedad estudiada. Estos datos permiten el cálculo de las estimaciones convencionales de las tasas por máxima verosimilitud, bajo el supuesto de que la variable estudiada (por ejemplo, número de defunciones observadas en un lapso dado) sigue una distribución Poisson. Como vimos, cuando se trabaja con áreas pequeñas, es muy posible que se obtengan estimaciones extremas de las tasas en algunas de ellas. De modo que resulta razonable admitir que las estimaciones obtenidas dependen de nuestro conocimiento, o de nuestra creencia sobre qué otras áreas pudieran tener tasas similares a las de aquellas en que hay pocos datos. Para proceder en esa dirección, se suelen definir unas “adyacencias” a partir de criterios tales como proximidad geográfica, similitud en materia económica, demográfica, etc. Esto es lo que configura la información a priori. En el caso más simple, operando como si hubiera una total ignorancia, se atribuye a las áreas “conflictivas” la media de todas las áreas presentes en el estudio.

Es obvio que si los casos observados son pocos y el monto de personas-tiempo reducido, entonces la información a priori será dominante; pero si el monto informativo es alto, entonces el peso de la información local será tanto o más importante que el de la contextual.

La creencia a priori sobre las distintas áreas geográficas puede ser representada por una distribución de probabilidad que estará centrada en el valor que en principio sea más creíble, y tendrá una variabilidad inversamente proporcional al grado de certidumbre que quepa atribuir a esa creencia.

Desde un punto de vista formal, tal enfoque se ajusta adecuadamente a la teoría de los modelos jerárquicos bayesianos. En el presente contexto, el teorema de Bayes permite obtener la distribución a posteriori para las tasas desconocidas como una magnitud proporcional al producto de la distribución a priori y la verosimilitud de los datos. La estimación de la tasa es entonces una medida central de la distribución a posteriori.

Procede aquí tener en cuenta que, si bien las REM pueden interpretarse como estimaciones de máxima verosimilitud del riesgo relativo (RR) bajo un modelo de Poisson, para enfermedades raras y áreas pequeñas, en cuyo contexto los riesgos individuales son heterogéneos, la variabilidad del riesgo relativo dentro de cada área excede al que se podía esperar para una distribución de Poisson. Esta variación “extra-Poisson” se puede manejar considerando los riesgos relativos dentro de cada área como una variable. Los métodos bayesianos se pueden usar con tal finalidad, y producir así estimaciones suavizadas de las REM.

Clayton y Kaldor8 hicieron una propuesta bayesiana para la modelación de los riesgos relativos, y para evitar así la mencionada inestabilidad de las REM crudas que se ubicarían en el mapa. La idea básica consiste en imponer una estructura a los riesgos relativos modelándolos colectivamente como un proceso estocástico espacial. En la modelación bayesiana esto significa que los riesgos relativos se suponen distribuidos de acuerdo con una distribución a priori multivariante, cuyos parámetros determinan aspectos tales como el nivel global del riesgo y la interdependencia geográfica entre los valores correspondientes a las áreas. La distribución a priori recoge información de todas las áreas del mapa; posteriormente, para cada área se produce una estimación del riesgo relativo que es un compromiso entre la REM cruda y la información que se obtiene de las áreas que la rodean. Las fluctuaciones de las REM crudas son así reducidas, y el mapa se “suaviza” (se “filtra” la variación de Poisson).

Supongamos que el área total que es objeto de estudio está dividida en n áreas contiguas representadas mediante los índices i =1,..,n. Llamemos O = (O1,... On) al vector que tiene por coordenada genérica Oi el número de casos de cierta enfermedad (o número de muertes) que se produjeron durante el período de estudio para la i-ésima área geográfica. El vector de casos esperados E = (E1,... En) se calcula aplicando a la población las tasas específicas por edad y sexo, asumiendo que éstas son constantes durante todo el período, tal y como se ilustró en la sección precedente. Llamemos x1 al riesgo relativo, desconocido, correspondiente a la i-ésima área, y denotemos por x = (x1,..., xn) al vector de los n riesgos relativos.

Lo que se quiere es tener una visión probabilística que combine lo observado con nuestra apreciación probabilística a priori. Es decir, los métodos bayesianos combinan los dos tipos de información: la que provee cada área a través de las muertes acaecidas (lo que permite calcular la verosimilitud suponiendo válido el modelo de Poisson) y la información a priori sobre los riesgos relativos. Coherentemente con el teorema de Bayes, la distribución a posteriori de los riesgos relativos viene dada por:

donde [O|x] es la verosimilitud y [x] la distribución a priori que se atribuya a los riesgos relativos. La función de verosimilitud es el producto de n distribuciones independientes de Poisson puesto que los Oi (i = 1,...,n) son mutuamente independientes y siguen una distribución de Poisson con media x1x1.

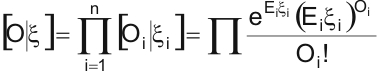
Bajo estas condiciones, el estimador de máxima verosimilitud de x i coincide con REM:

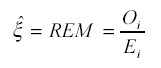
Para especificar la estructura a priori para xi existen diversas posibilidades, que van desde el modelo más simple, en el cual se considera un valor medio hacia el que tiende cada área, hasta los que postulan una compleja variante de interdependencia entre las áreas. En este trabajo se considera una estructura en la cual la estimación de los riesgos relativos en cada área solo depende de los riesgos relativos en las áreas contiguas o adyacentes. Como se parte de la creencia de que existen correlaciones espaciales entre los riesgos relativos (por ejemplo, que áreas geográficamente próximas tienden a tener riesgos relativos similares), se considera una estructura espacial de tal manera que aquellas áreas que rodean a una cierta área i tengan influencia sobre la estimación del riesgo relativo en ella (véase anexo).

El proceso de establecimiento de los valores a posteriori para los xi es considerablemente complejo desde el punto de vista computacional. Para conseguirlo hay que estimar los parámetros del modelo jerárquico, para lo cual se utilizan técnicas de simulación; en este caso se utiliza el Gibbs Sampler, que pertenece a la familia de métodos de Monte Carlo y Cadenas de Markov14 (MCMC), susceptible de ser aplicado usando el programa WinBugs.15

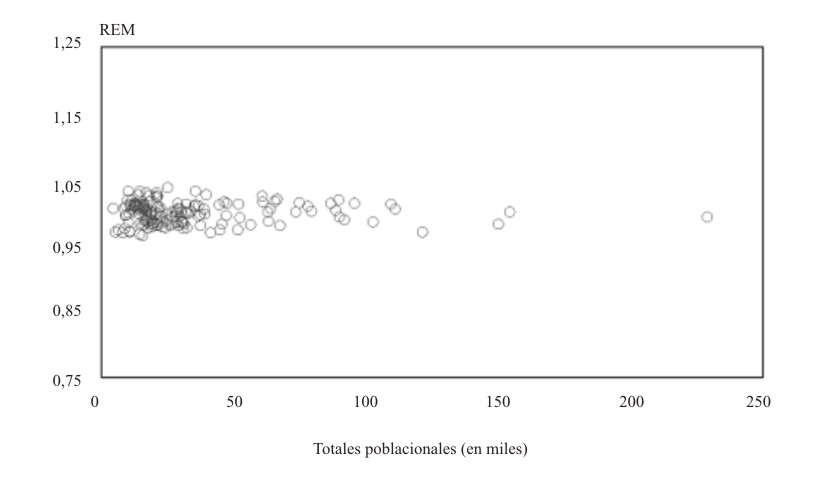
Al aplicar este complejo algoritmo, se obtienen las estimaciones a posteriori de los riesgos relativos, es decir, las REM suavizadas. Un análisis gráfico similar al de la figura 2, permite apreciar cómo la fuerte dependencia que tenían las REM con respecto al tamaño poblacional de las áreas, ha diminuido notablemente hasta casi desaparecer (fig. 3).

FIG. 3. Diagrama de dispersión de las REM suavizadas por accidentes en 1998 y los totales poblacionales para los 169 municipios de Cuba.

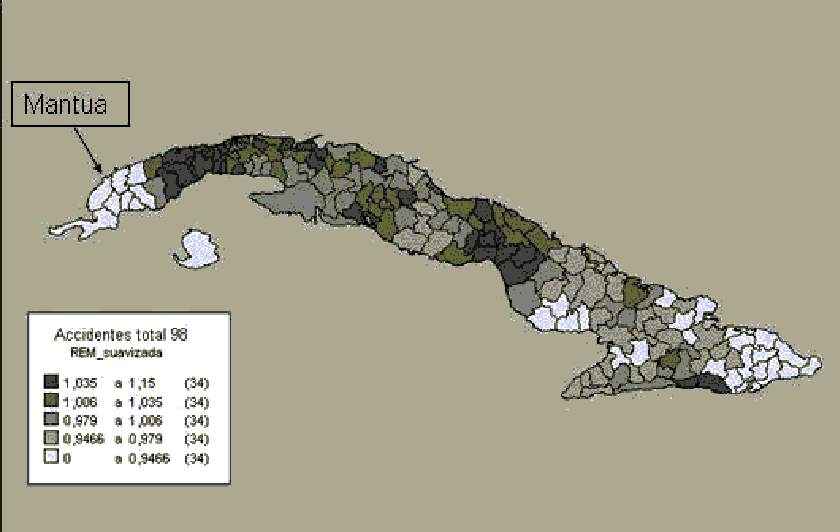
La figura 4 presenta la distribución geográfica de las REM calculadas según el método bayesiano explicado. Como en el mapa anterior, esta figura muestra en cinco tonos de gris cada una de las áreas ubicadas según categorías conformadas a partir de nuevos quintiles de la distribución de las REM.

En el mapa se observa nítidamente el efecto de la suavización, contrapuesto al que se confeccionó con las técnicas tradicionales. Ahora se revela con claridad el patrón de alta mortalidad por accidentes que exhiben los municipios más desarrollados (por ejemplo, capitales provinciales y polos turísticos).

A modo de complemento ilustrativo final veamos qué ocurrió en el municipio Mantua. Como se puede observar este último mapa (fig. 4), aparece representado en un tono más claro que antes, coherente con los municipios que lo rodean. A diferencia de lo que representa la figura 1, Mantua se identifica ahora como un área de bajo riesgo.

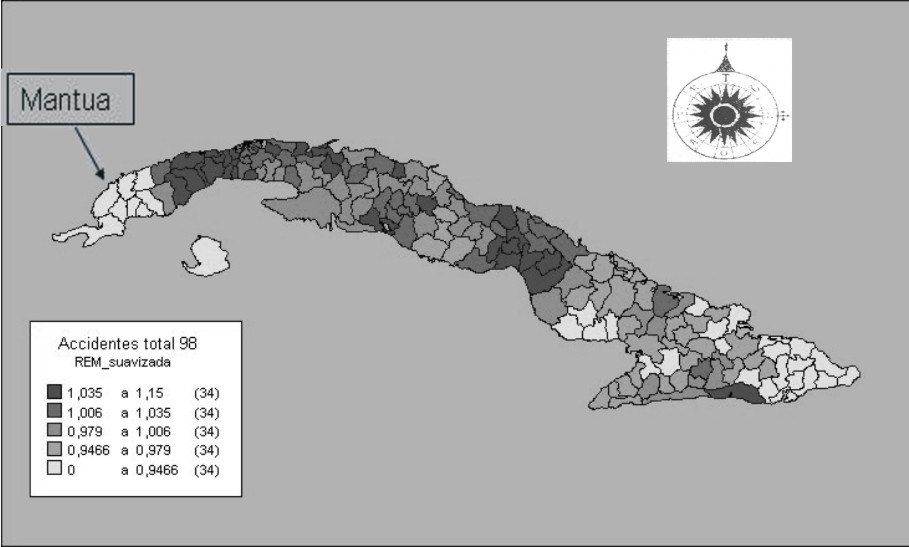
Fig. 4. Representación espacial de la razón estandarizada de mortalidad por accidentes suavizada para todos los municipios de Cuba, año 1998.
Escala 1: 1 000 000

Desde luego, quizás no haga falta aplicar este complejo procedimiento para “descubrir” esta realidad -que la accidentalidad es más acusada en los espacios de mayor desarrollo económico social. En este ejemplo, nuestro análisis tiene sobre todo valor como recurso demostrativo, y en cierto sentido, como vehículo de validación de una técnica estadística y como medio de validar; pero es razonable esperar que para otras dolencias o causas de muerte, los patrones espaciales pueden emerger de modo inesperado para el investigador y abrirle así espacios de indagación novedosos, como ya demuestra una amplia experiencia internacional en esta materia.16-19

ANEXO: Modelo jerárquico bayesiano

Utilizando la notación anterior, sea Oi el número de casos observados, Ei el número de casos esperados y x i el riesgo relativo en el municipio i-ésimo (i=1,...,169).
Conocido el riesgo relativo, el número de casos observados sigue una distribución de Poisson:

• Asumimos el siguiente modelo para los riesgos relativos: el logaritmo de x1 se puede expresar como la suma de una media global m (efecto fijo) y una componente aleatoria Æi (dependiente del área) que se puede conceptuar como el efecto de ciertas variables desconocidas y no observadas que afectan al riesgo. Esto es:

de modo que:

La modelación bayesiana requiere de la especificación de distribuciones a priori para todos los efectos aleatorios y parámetros del modelo descrito anteriormente; es decir, hay que establecer distribuciones para m y para fi.

Para la media global m es razonable asumir que nuestra ignorancia es total; por lo tanto se le puede asignar una distribución no informativa en la recta real, lo cual es básicamente equivalente a asumir que m ~ normal (0,108).

Para la componente espacial fi se utiliza una estructura de correlación espacial tal que las estimaciones en un área dependan de las áreas vecinas.20 Así pues fi sigue una distribución normal con varianza inversamente proporcional al número de unidades adyacentes a la i-ésima y a cierto hiperparámetrol. Concretamente:

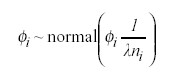
donde ni es igual al número de vecinos del área y (V es el conjunto de los vecinos del área i).

Finalmente, para que el modelo quede totalmente definido, es necesario dotar a l con una distribución a priori. Bernardinelli, Clayton y Montomoli21 recomiendan el uso de una distribución gamma para este hiperparámetro. En este trabajo tomamos l~gamma (0.5,0.0005). Utilizando el modelo y las estructuras a priori presentadas en este anexo se obtienen las estimaciones suavizadas del riesgo relativo que se muestran en la figura 4.

Summary

Using maps to represent relevant health data probably provides a more expressive image of their spatial distribution than the simple tables. Through the map it is possible to grasp geographic distribution patterns as well as to suggest possible explanations on identified distributions. For this reason the smoothed construction of disease maps has been the object of recent methodological developments. The traditional approach consists of plotting on a map the standardised mortality ratios. However, when the number of cases in small geographical areas is low, crude mortality rates are very labile, and their representation in maps shows a wide and scarcely informative variation of the existing patterns. Bayesian methods offer the possibility of “correcting” the maps, so that patterns that are not visible when traditional statistical procedures are used can emerge. In order to illustrate and to explain in more detail both methods, mortality data coming from accidents in Cuba for 1998 were used. For this analysis the population was divided in 7 age groups: 0 to 14, 15 to 24, 25 to 34, 35 to 44, 45 to 54, 55 to 64 and 65 and more; as geographic areas we considered the 169 Cuban municipalities. Two maps are shown: one made according to traditional methods, and another one according to the Bayesian ones. In the latter the effect of the smoothing can be clearly observed; the space pattern of mortality, previously diffuse, allows to appreciate that mortality from accidents is specially remarkable in the developed municipalities.

Subject headings: RESIDENCE CHARACTERISTICS/ statistics numerical data; HEALTH; MAPS; GEOGRAPHIC LOCATIONS; MORTALITY; POPULATION DENSITY; CUBA.

Referencias bibliográficas

1. Greenland S, Morgenstein H. Ecologic bias, confounding, and effect modification. Int J Epidemiol 1987;16:111-20.
   
2. Clayton DG, Bernardinelli L, Montomoli C. Spatial correlation in ecological analysis. Int J Epidemiol 1993; 22(6):1193-1201.
   
3. Walter SD. The ecologic method in the study of environmental health. Overview of the method. Environm Health Perspec 1991;94:61-65.
   
4. Lawson AB, Cressie N. Spatial statistical methods for environmental epidemiology. En: Sen PK, Rao CR, eds. Handbook of statistics. vol 18. Amsterdam: Elsevier Science; 2000.
   
5. Wakefield JC, Kelsall JE, Morris SE. Clustering, cluster detection and spatial variation in risk. En: Elliott P, Wakefield J, Best NG, Briggs D, eds. Spatial epidemiology. Methods and Applications. Oxford: Oxford University Press; 2000.
   
6. Lopez-Abente G, Pollán M, Escolar A, Errezola M, Abraira V. Atlas of cancer morta-lity and other causes of death in Spain 1978-1992. Madrid: Instituto de Salud Carlos III; 2001.
   
7. Lawson AB, Bohning D, Biggeri A, Lesaffre E, Viel JF. Disease mapping and its uses. En: Lawson AB, Boehning D, Lasaffree E, Biggeri A, Viel JF, Bertolline R, eds. Disease mapping and risk assessment for public health. Chichester: Wiley; 1999.
   
8. Clayton DG, Kaldor J. Empirical bayes estimates of age-standardized relative risk for use in disease mapping. Biometrics 1987;43:671-681.
   
9. Wakefield JC, Best NG, Waller L. Bayesian approaches to disease mapping. En: Elliott P, Wakefield J, Best NG, Briggs D, eds. Spatial Epidemiology. Methods and applications. Oxford: Oxford University Press; 2000.
   
10. Breslow NE. Biostatistics and Bayes. Stat Sci 1990;5(3):269-298.
    
11. Rue M, Borrel C. Los métodos de estandarización de tasas. Revisiones en Salud Pública 1993;3:263-95.
    
12. Breslow NE, Day NE. Indirect standarization and multiplicative models for rates, with reference to age adjustment of cancer incidence and relative frequency data. J Chron Dis 1975;28:289-303.
    
13. Silva LC, Benavides A. El enfoque bayesiano: otra forma de inferir. Gac Sanit 2001; 15(4):341-346.
    
14. Gilks WR, Richardson S, Spiegelhalter DJ, eds. Markov Chain Monte Carlo in Practice. London: Chapman & Hall; 1996.
    
15. Spiegelhalter DJ, Thomas A, Best NG. WinBugs: Version 1.3. User manual. Cambridge: MRC Biostatistics Unit; 2000.
    
16. Bernardinelli L, Pascutto C, Montomoli C, Gilks WR. Investigating the genetic association between diabetes and malaria: an application of Bayesian ecological regression models with errors in covariates. En: Elliott P, Wakefield J, Best NG, Briggs D. eds. Spatial Epidemiology. Methods and applications. Oxford: Oxford University Press; 2000.
    
17. Knorr-Held L. Bayesian modelling of inseparable space-time variation in disease risk. Stat Med 2000;19:2555-2567.
    
18. MacNab YC, Dean CB. Spatio-temporal modelling of rates for the construction of disease maps. Stat Med 2002;21:347-58.
    
19. Steward J, John G. An ecological investigation of the incidence of cancer in Welsh children for the period 1985-1994 in relation to residence near the coast line. J Roy Stat Soc 2001 A; 164:29-43.
    
20. Besag J, York J, Mollié A. A Bayesian image restoration, with two applications in spatial statistics (with discussion). Ann Inst Stat Mathem 1991;43:1-59.
    
21. Bernardinelli L, Clayton D, Montomoli C. Bayesian estimates of disease maps: how important are priors? Stat Med 1995;14:2411-31.

Recibido: 18 de abril de 2003. Aprobado: 18 de junio de 2003.
Luis Carlos Silva Aycaguer. Instituto Superior de Ciencias Médicas de La Habana. E-mail: [e-mail]

* Ponencia presentada en el II Seminario Nacional “Espacio y salud: lugar, salud y enfermedad. Universidad de La Habana; 17-18 de abril de 2003.
1 Investigador Titular.
2 Especialista de I Grado en Bioestadística. Hospital Universitario “Arnaldo Milián Castro”, Villa Clara.
3 Licenciada en Matemáticas, Department of Epidemiology and Biostatistics, Norman J. Arnold School of Public Health, University of South Carolina.