ARTÍCULOS DE REVISIÓN

 

Aplicabilidad de la simulación computacional en la biomecánica del disco Óptico

 

Applicability of computational simulation in the biomechanics of the optic disc

 

 

Ing. Bernardo Calderín Pérez ^I; Dr. C. Raide Alfonso González Carbonell ^II; Dr C. Matilde Landín Sorí ^III; Dr. C. Elsa Nápoles Padrón^II

I Centro provincial de electromedicina.Camagüey, Cuba.
II Universidad de Camagüey Ignacio Agramonte Loynaz. Camagüey, Cuba.
III Hospital Universitario Manuel Ascunce Domenech. Camagüey, Cuba.

 

 

---

RESUMEN

Fundamento: la presión intraocular provoca tensiones y deformaciones en los tejidos del disco óptico que pueden ocasionar daño glaucomatoso.
Objetivo: simular el comportamiento biomecánico del disco óptico y describir su aplicabilidad en la predicción del daño glaucomatoso.
Métodos: la herramienta de simulación computacional usada es el Método de Elementos Finitos. Se utilizó una presión intraocular de 15 mm Hg, así como las propiedades mecánicas y la geometría de los tejidos de la papila óptica reportados en la literatura.
Desarrollo: las mayores concentraciones de tensiones aparecen a nivel de la esclerótica peripapilar y fueron congruentes con las estimaciones reportadas en la literatura. La rigidez escleral influyó sobre las tensiones transmitidas a la lámina cribosa. Este tejido resultó ser el más susceptible al daño glaucomatoso dentro de la papila óptica.
Conclusiones: el análisis preliminar obtenido constituye un punto de partida para el estudio del nervio óptico a través de la simulación computacional. Se demuestra que la presión intraocular, la complejidad de la geometría y las propiedades mecánicas de los tejidos de la cabeza del nervio óptico son factores condicionantes del daño glaucomatoso.

DeSC:PRESIÓN INTRAOCULAR; GLAUCOMA; FENÓMENOS BIOMECÁNICOS; DISCO ÓPTICO; LITERATURA DE REVISIÓN COMO ASUNTO. 

---

ABSTRACT

Background: intraocular pressure causes tension and deformities in the tissues of the optical disc that can entail glaucomatous damage.
Objective: to simulate the biomechanical behaviour of the optical disc and describe its applicability in the prediction of glaucomatous damage.
Method: Finite Element Method was the computational simulation tool used. An intraocular pressure of 15 mm Hg was used, as well as the mechanical properties and geometry of tissues of the optic papilla reported in the literature.
Development: most of the concentrations of tension appear at the level of the peripapillary sclera and were consistent with the estimations reported in the literature. Scleral stiffness had an influence on the tension transmitted to the lamina cribosa sclerae. This tissue was the most susceptible to glaucomatous damage in the optical papilla.
Conclusions: the preliminary obtained analysis is a starting point for the study of the optic nerve by means of the computational simulation. It was proved that intraocular pressure, the complexity of the geometry and the mechanical characteristics of the tissues of the head of the optic nerve are determining factors of the glaucomatous damage.

DeSC: INTRAOCULAR PRESSURE; GLAUCOMA; BIOMECHANICAL PHENOMENA; OPTIC DISK; REVIEW LITERATURE AS TOPIC. 

---

 

 

INTRODUCCIÓN

Muchas enfermedades le provocan al ser humano la pérdida total o parcial de la visión, ¹ por ejemplo: catarata, neuropatías ópticas, tracoma, retinopatía diabética, etc. y a pesar que se actualizan los tratamientos,² los protocolos, ³ y los novedosos medios de diagnóstico como el tomógrafo retiniano Heidelberg, (HRT), ⁴ el tomógrafo de coherencia óptica (OCT) y la polarimetría láser, ⁵ los índices de personas discapacitadas son altos, aunque un gran porciento  de estas enfermedades se pueden evitar o curar.

Dentro de las neuropatías ópticas se distingue el glaucoma. Según Burgoyne, et al, ⁶ el daño glaucomatoso es gobernado por la distribución de tensiones y deformaciones provocadas por la presión intraocular (PIO) sobre los tejidos del disco óptico o papila óptica; independientemente de la magnitud a la que ocurre. ⁷

En las últimas décadas, dos hipótesis fundamentales se consideran como las responsables del daño glaucomatoso: la afectación del suministro de sangre a la cabeza del nervio óptico (hipótesis vascular) y la elevación de la PIO (hipótesis mecánica) donde la papila óptica se analiza como una estructura biomecánica.  ^8,9

Como argumentó Burgoyne, et al, ⁶ la influencia de la tensión y la deformación provocadas por la PIO dentro del tejido conectivo, son centrales tanto para la fisiología como la fisiopatología de los tejido que conforman la cabeza del nervio óptico.

Los modelos biomecánicos han tenido un vertiginoso auge en los últimos años, muy favorecidos por el considerable desarrollo de la informática. La simulación computacional vinculado con el glaucoma es beneficiado por tales avances, ^8,10 fundamentalmente con la implementación del método de elementos finitos (MEF), ^11,12 soportado en software profesionales. Aunque no existe una solución definitiva al grave problema que representa la neuropatía óptica glaucomatosa, los modelos biomecánicos demuestran ser un pilar en la búsqueda de ese resultado.

Explorar el campo de la aplicación de la biomecánica con fines de diagnóstico de las enfermedades oculares tiene un escenario favorable tanto en Cuba como en Camagüey, donde los especialistas de la salud cuentan con gran experiencia en la Oftalmología. ¹³ El objetivo de este trabajo es simular el comportamiento biomecánico del disco óptico y describir su aplicabilidad en la predicción del daño glaucomatoso.

 

DESARROLLO

Los modelos más consistentes, desde un enfoque físico, son los basados en ecuaciones de la mecánica continua no lineales; los cuales generalmente son resueltos mediante métodos numéricos como el MEF.

Este método consiste en aproximar la geometría mediante la división del modelo en pequeñas porciones, conocidas como elementos finitos. Se utiliza en el presente estudio debido a la complejidad de la geometría y de las propiedades de los tejidos que conforman el disco óptico.

Según González, et al, ¹⁴ los modelos mecánicos están definidos por el modelo geométrico, el modelo de carga (interacción entre los elementos) y el modelo de material (leyes, principios e hipótesis). Los fundamentos usados en la definición del modelo serán descritos a continuación.

Geometría de la cabeza del nervio óptico.

La geometría de los tejidos del disco óptico relacionados con el daño glaucomatoso es muy compleja. En primer lugar por el difícil acceso al interior del globo ocular, en segundo lugar por las dimensiones tan pequeñas que éstas presentan y en tercer lugar porque el equipamiento para la obtención de modelos con parámetros geométricos reales es muy costoso. ^15,16

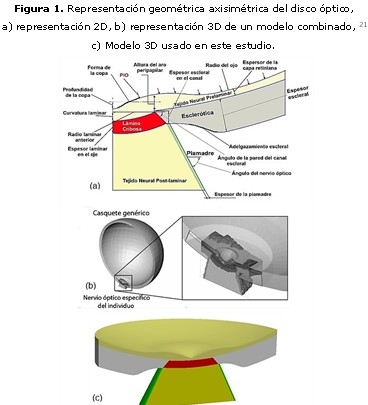
En los primeros intentos significativos de análisis biomecánico del disco óptico, la representación geométrica se limitó a lo dominios de la geometría bidimensional (2D). Sigal, et al, ¹⁷ construyó tres modelos axisimétricos 2D a través de la variación independiente del espesor escleral, el diámetro del canal escleral y la forma de la copa óptica. Los detalles fisiológicos utilizados en esos modelos se basaron en datos reportados en la literatura y otros provenientes de resultados experimentales. En el tercer modelo están incluidos la piamadre y el adelgazamiento escleral peripapilar, que no fueron considerados en los anteriores modelos (figura 1a).

Posteriormente fue evaluado el efecto de 21 factores, entre anatómicos y biomecánicos, en la respuesta biomecánica del disco óptico.¹⁸ Se determinó que la rigidez escleral (módulo de Young), el radio del globo ocular, la rigidez de la lámina cribosa (LC), la PIO y el espesor de la esclerótica peripapilar son, en este orden, los cinco factores más sensibles a los cambios de PIO.

Los modelos tridimensionales (3D) de las geometrías reales de la cabeza del nervio óptico están agrupados en:

1) modelos genéricos obtenidos virtualmente, donde se pueden modificar los parámetros implicados de forma independiente.
2) modelos específicos–individuales (técnicas de histomorfometría), ¹⁹ estos son muy congruentes con los detalles geométricos del tejido In vivo, pero su generalización es limitada por el número y la diversificación de los especímenes.
3) La combinación de ambas aproximaciones (figura 1b). ^11,15

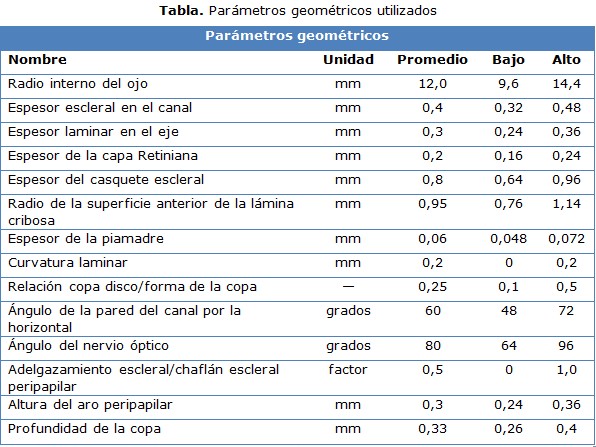
Debido a las limitaciones y complejidad de la histomorfometría, el presente trabajo se elaboró sobre un modelo genérico tridimensional, a partir del tercer modelo realizado por Sigal, et al, ¹⁷ (figura 1c), cuyos parámetros geométricos aparecen en la tabla, sintetizados de la literatura consultada. ^17,18,20

Propiedades mecánicas de los tejidos de la cabeza del nervio óptico.

Como afirmó González, et al, ¹⁴ las propiedades del material son esenciales en el modelado. Cuando la esclerótica y la LC son rígidas, contribuyen a disminuir las deformaciones dentro de la cabeza del nervio óptico.  ²¹ Por otra parte, la rigidez de la esclerótica produce 10 veces más cambios en las deformaciones compresivas medias dentro del tejido neural prelaminar que las diferencias geométricas. ¹⁸ A partir de la modificación de las propiedades mecánicas de la esclerótica de ratones, se han planteado estrategias de tratamiento sobre una nueva aproximación terapéutica al glaucoma, basados en la reducción de la tensión generada por la PIO en la papila óptica. ²² Grytz, et al, ¹⁶ reportó estimaciones de propiedades del material de la esclerótica peripapilar humana posterior que incorpora la naturaleza no homogénea, hiperelástica y anisotrópica del tejido; sus resultados fueron muy compatibles con otras aproximaciones de caracterización de material. ²³

Las propiedades del material, reportadas en la literatura revisada, ^{11, 21, 24, 25} para los tejidos más influyentes en el comportamiento biomecánico del disco óptico, son las siguientes:

• Para la esclerótica, el módulo de Young entre 1 y 9 MPa. Con la excepción de Eilaghi, et al, ¹² que considera la esclerótica como un material hiperelástico.
• La lámina cribosa, entre 0, 0055 y 0, 9 MPa.
• Los tejidos neurales prelaminar y post-laminar, entre 0, 01 y 0, 09 MPa.
• La piamadre, entre 1 y 9 MPa.
• Un coeficiente de Poisson, entre 0, 49 y 0, 5.

Por su reiteración en las investigaciones consultadas, en la definición de las propiedades mecánicas a emplear, en este trabajo se utilizan: el módulo de Young de 3 MPa para la esclerótica; 0, 3 MPa para la LC; 0, 03 MPa para los tejidos neurales, ³ MPa para la piamadre, y un coeficiente de Poisson de 0, 49 (prácticamente incompresible). De manera análoga, con el objetivo de simplificar el estudio, todos los materiales fueron asumidos como elásticos, isotrópicos e incompresibles.

Presión intraocular y restricciones del modelo.

Fue definido el modelo de carga a través de la presión intraocular como una entidad mecánica (fuerza normal por unidad de área, ejercida por los fluidos intraoculares sobre los tejidos que la contienen). La cual experimenta fluctuaciones debido a los ritmos circadianos. ²⁶

Estadísticamente la bibliografía médica ²⁶ considera la PIO normal de 10 a 21 mm Hg, pero en la actualidad no están definidos claramente los rangos de PIO que permitan diferenciar a los ojos normales de los glaucomatosos o de los hipertensos oculares; puesto que la respuesta biomecánica del ojo a la presión intraocular varía de un individuo a otro por múltiples factores.

Según Bellezza, et al, ⁷ para valores de PIO normales (alrededor de 15 mm Hg) la papila óptica está sometida a tensiones substanciales, concentradas mayormente en las regiones de la esclerótica peripapilar, el canal escleral, y la lámina cribosa. En las modelaciones reportadas en la literatura, la PIO es aplicada como una carga estática distribuida uniformemente en toda la superficie interior del globo ocular. Los valores usados en las simulaciones computacionales oscilan entre 5 y 50 mm Hg. ^9,16,20 En el presente estudio la PIO es 15 mm Hg.

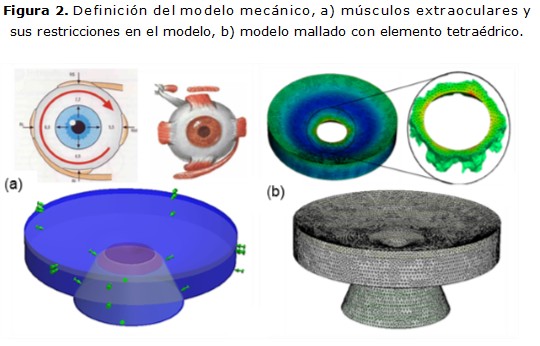
Las condiciones de contorno son definidas como restricciones de movimiento del modelo y son las que expresan la interacción del modelo con el organismo. Se eliminaron los desplazamientos radiales en el eje ecuatorial del ojo; equivalente, de forma aproximada, con las restricciones que generan los músculos extraoculares. El resto de las restricciones fueron aplicadas de manera que el globo ocular solo se deforme en la dirección del eje de simetría (figura 2a).

Aunque el globo ocular presenta deformaciones generales bajo la acción de la PIO, solo se modelaron sus efectos sobre la región de la cabeza del nervio óptico, limitados a 5º del centro del eje de simetría consecuente con los 10º del campo de adquisición de la HRT. ¹⁷ Se empleó el método de mallado compatible auto-adaptativo (h-method), con el propósito de reducir el tamaño de los elementos en las zonas donde las tensiones son mayores. El cálculo de las tensiones es más preciso, se incrementa la calidad de la malla en la zona de interés del análisis (figura 2b), se logra una unión rígida entre los elementos del ensamble, los que se deforman y desplazan en conjunto.

Simulación biomecánica de la cabeza del nervio óptico.

Cuando se analiza un objeto tridimensional sometido a cargas, las reacciones internas que aparecen en su interior se oponen a las fuerzas externas. De esta manera surgen las tensiones en el interior del cuerpo (densidad de fuerza por unidad de área). Si se considera un elemento infinitesimal en el interior del nervio óptico en forma de cubo, en cada una de las caras aparecen tensiones normales y tangenciales. A través de una de las teorías de resistencia se obtiene la tensión equivalente de cada elemento infinitesimal. Para determinar dichas tensiones, se seleccionó la teoría de la energía potencial de deformación o también conocida como de von Mises. La interpretación de los resultados se basó en las tensiones equivalentes máximas de von Mises expresadas en múltiplos de PIO y en los desplazamientos.

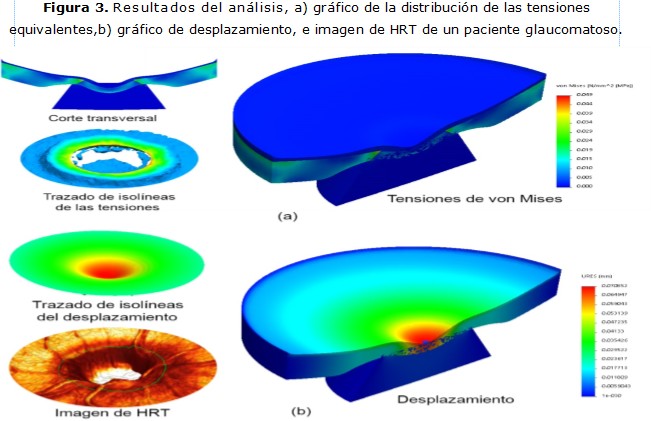
De los resultados de la simulación por el MEF se observó la distribución de las tensiones en todo el volumen del cuerpo (figura 3).

En la figura 3a, el gráfico de isolíneas muestra como las mayores tensiones equivalentes (13 x PIO) se concentraron a nivel de la esclerótica peripapilar (en la pared del canal escleral), las que fueron congruentes, en magnitud y localización, con las estimaciones reportadas.^9,11,12,17 Esto confirma la influencia de la rigidez escleral como soporte de las tensiones que se trasmiten a la LC, que por sus propiedades es el tejido más susceptible al daño glaucomatoso dentro del disco óptico. ^9,18

La interpretación de la concentración de tensiones desde el punto de vista físico se debe a que la LC se encuentra unida a la esclerótica. ¹⁵ Al aplicar la PIO sobre el tejido neural preliminar (que se modela con un comportamiento quasi-incompresible) se transmite a la lámina cribosa. Como respuesta a la presión intraocular, la lámina cribosa se deforma y en la zona de unión con la esclerótica se generan fuerzas internas en oposición a la deformación.

Los mayores desplazamientos dentro del modelo se ubicaron en el centro de la papila óptica. Si se compara el trazado de isolíneas y la imagen proveniente del HRT para un paciente con daño glaucomatoso (figura 3b) se puede apreciar que la cabeza del nervio óptico posee el comportamiento pronosticado en la simulación. O sea, que existe coincidencia del lugar donde ocurre la excavación óptica, con las estimaciones computacionales.

La deformación o adelgazamiento del tejido neural prelaminar observado en el modelo (350 µm) estuvo dentro del rango de valores que se obtienen en los medios de diagnóstico para este fin, como la OCT ²⁷ o la polarimetría láser; ²⁸ y no es más que la respuesta a la compresión que ejerce la PIO sobre la capa de fibras neurorretinianas.

Existen varios factores como la expansión lateral del canal escleral, deformación de las superficies anterior-posterior de la LC, rotación de la esclerótica peripapilar, etc., que deben ser tomados en cuenta y que su efecto se analizó previamente en otros artículos,²⁸ donde se demostró que al variar la geometría y las propiedades mecánicas de los elementos de la papila óptica, en conjunto con esos factores, se modifica la respuesta biomecánica de la cabeza del nervio óptico.

Finalmente, para elevar la confiabilidad de los estudios y que sus resultados puedan ser utilizados en el diagnóstico de pacientes glaucomatosos, se requiere de modelos específicos-individuales, que se obtienen a través un complejo procesamiento de imágenes y de establecer relaciones que permitan reducir las diferencias entre las propiedades mecánicas del individuo y las reportadas tradicionalmente en la literatura.

Por otra parte, la confiabilidad de la simulación computacional se puede incrementar al vincular los parámetros geométricos obtenidos en los medios de diagnósticos con la geometría y al conceptuar modelos constitutivos de material que consideren los tejidos blandos de la cabeza del nervio óptico con una naturaleza no homogénea, hiperelástica y anisotrópica.

 

CONCLUSIONES

La simulación computacional preliminar del comportamiento biomecánico del disco óptico sometido a presión intraocular fue realizada. Se muestran los fundamentos para definir los elementos del modelo del disco óptico: la presión intraocular, la complejidad de la geometría y las propiedades mecánicas. Los resultados confirman que estos son factores condicionantes de la concentración de tensiones, las deformaciones y los desplazamientos en el tejido conectivo que soporta la carga dentro del disco óptico.

La localización y magnitud de las tensiones y desplazamientos obtenidos permite afirmar que es posible aplicar la simulación computacional como herramienta de apoyo para comprender el comportamiento del disco óptico. Los resultados serán más confiables a medida que la definición de los elementos del modelo sean más precisos y específicos al paciente.

 

REFERENCIAS BIBLIOGRÁFICAS

1. Pascolini D, Mariotti SP. Global estimates of visual impairment: 2010. Br J Ophthalmol. 2012 Dic;96(5):25-35.

2. Panda Jonas S, Xu L, Yang H, Wang YX, Jonas SB, Jonas JB. Optic nerve head morphology in young patients after antiglaucomatous filtering surgery. Acta Ophthalmol. 2014 Feb;92(1):46-78.

3. Eguía Martínez F, Rió Torres M, Capote Cabrera A. Manual de Diagnóstico y Tratamiento en Oftalmología. La Habana: ECIMED; 2009.

4. Balasubramanian M, Bowd C, Weinreb RN, Zangwill LM. Agreement between the Heidelberg Retina Tomograph (HRT) stereometric parameters estimated using HRT-I and HRT-II. Optom Vis Sci. 2011 Ene; 88(1):140-9.

5. Sigal IA, Grimm JL, Schuman JS, Kagemann L, Ishikawa H, Wollstein G. A Method to Estimate Biomechanics and Mechanical Properties of Optic Nerve Head Tissues From Parameters Measurable Using Optical Coherence Tomography. IEEE Transactions on Medical Imaging. 2014 Jun;33(6):1381-9.

6. Burgoyne CF, Downs JC, Bellezza AJ, Suh FJK, Hart RT. The optic nerve head as a biomechanical structure: a new paradigm for understanding the role of IOP-related stress and strain in the pathophysiology of glaucomatous optic nerve head damage. Prog Retin Eye Res. 2005 Ene;24(1):39-73.

7. Bellezza AJ, Hart RT, Burgoyne CF. The Optic Nerve Head as a Biomechanical Structure: Initial Finite Element Modeling. Invest Ophthalmol Vis Sci. 2000 Sep;41(10):2991-3000.

8. Gaddie B, Bloomenstein M, Thimons J, Wooldridge R. Using Biomechanics to Advance Glaucoma Care. Optometric Management. 2013 Feb:3-11.

9. Sigal IA, Grimm JL. A Few Good Responses: Which Mechanical Effects of IOP on the ONH to Study? Invest Ophthalmol Vis Sci. 2012 Abr;53(7):4270-8.

10. González Carbonell RA, Nápoles Padrón E, Claderín Pérez B, Hidalgo Cisneros YA, Landín Sorí M. Interdisciplinariedad entre Ingeniería y Medicina en problemas de salud. Rev Hum Med. 2014. De proxima aparición.

11. Norman RE, Flanagan JG, Sigal IA, Rausch SM, Tertinegg I, Ethier CR. Finite element modeling of the human sclera: influence on optic nerve head biomechanics and connections with glaucoma. Exp Eye Res. 2011 Jul;93(1):4-12.

12. Eilaghi A, Flanagan JG, Simmons CA, Ethier CR. Effects of scleral stiffness properties on optic nerve head biomechanics. Ann Biomed Eng. 2010 Abr;38(4):1586-92.

13. Landín Sorí M, Rodríguez Bencomo DdJ. Una aproximación a la historia de la Oftalmología en Camagüey. Rev Hum Med. May-Ago 2014;14(2):271-84.

14. González Carbonell R, Alvarez García E, Moya Rodríguez J. Tacón de Torque para uso Ortopédico: Propuesta de un Nuevo Diseño. En: Folgueras Méndez J, Aznielle Rodríguez TY, Calderón Marín CF, Llanusa Ruiz SB, Castro Medina J, Vega Vázquez H, et al, editores. V Latin American Congress on Biomedical Engineering CLAIB 2011. IFMBE Proceedings. 33. Berlin Heidelberg: Springer; 2013. p. 912-5.

15. Sigal IA, Flanagan JG, Tertinegg I, Ethier CR. 3D morphometry of the human optic nerve head. Exp Eye Res. 2010 Ene;90(1):70-80.

16. Grytz R, Fazio MA, Girard MJA, Libertiaux V, Bruno L, Gardiner S, et al. Material properties of the posterior human sclera. J Mech Behav Biomed. 2014 Ene;29:602-17.

17. Sigal IA, Flanagan JG, Tertinegg I, Ethier CR. Finite Element Modeling of Optic Nerve Head Biomechanics. Invest Ophthalmol Vis Sci. 2004 Ago;45(12):4378-87.

18. Sigal IA, Flanagan JG, Ethier CR. Factors Influencing Optic Nerve Head Biomechanics. Invest Ophthalmol Vis Sci. 2005 Nov;46(11):4189-99.

19. Qiu J, Qian X, Quan H, Wangjun O, Liu Z. The in vivo 3D Optic nerve head modeling based on human multimodality images. En: Long M, editor. World Congress on Medical Physics and Biomedical Engineering 2012. IFMBE Proceedings. 39. Berlin Heidelberg: Springer; 2013. p. 264-6.

20. Sigal IA. Interactions between geometry and mechanical properties on the optic nerve head. Invest Ophthalmol Vis Sci. 2009 Abr;50(6):2785-95.

21. Sigal I, Flanagan J, Tertinegg I, Ethier CR. Modeling individual-specific human optic nerve head biomechanics. Part II: influence of material properties. Biomech Model Mechan. 2009 Abr;8(2):99-109.

22. Quigley H, Cone F. Development of diagnostic and treatment strategies for glaucoma through understanding and modifiction of scleral and lamina cribrosa connective tissue. Cell Tissue Res. 2013 Ago;353(2):231-44.

23. Girard MJA, Downs JC, Burgoyne CF, Suh JKF. Peripapillary and Posterior Scleral Mechanics—Part I: Development of an Anisotropic Hyperelastic Constitutive Model. J Biomech Eng. 2009 May;131(5):051011 1-9.

24. Sigal IA, Bilonick RA, Kagemann L, Wollstein G, Ishikawa H, Schuman JS, et al. The optic nerve head as a robust biomechanical system. Invest Ophthalmol Vis Sci. 2012 May;53(6):2658-67.

25. Sigal IA, Flanagan JG, Lathrop KL, Tertinegg I, Bilonick R. Human lamina cribrosa insertion and age. Invest Ophthalmol Vis Sci. 2012 Ago;53(11):6870-9.

26. Bilonick R. Human lamina cribrosa insertion and age. Invest Ophthalmol Vis Sci. 2012 Ago;53(11):6870-9.

27. CTO G. Manual CTO de Medicina y Cirugía. 8va ed. CTO Medicina; 2011.

28. Mwanza J-C, Chang RT, Budenz DL, Durbin MK, Gendy MG, Shi W, et al. Reproducibility of Peripapillary Retinal Nerve Fiber Layer Thickness and Optic Nerve Head Parameters Measured with Cirrus HD-OCT in Glaucomatous Eyes. Invest Ophthalmol Vis Sci. 2010 Nov;51(11):5724-30.

 

 

Recibido: 12 de noviembre de 2014
Aprobado: 3 de diciembre de 2014

 

 

Ing. Bernardo Calderín Pérez.  Ingeniero Mecánico. Centro Provincial de Electromedicina. Camagüey, Cuba. Email: [e-mail]