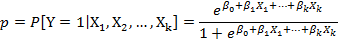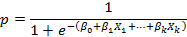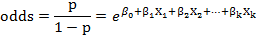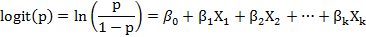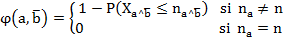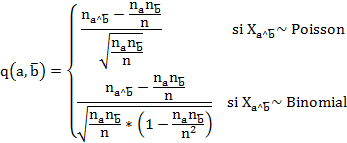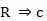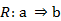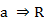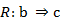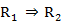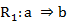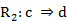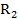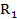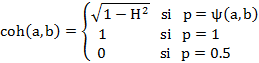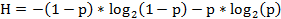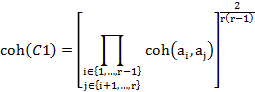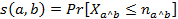Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
Uno de los elementos que más ha contribuido al avance de la investigación médica en los últimos años ha sido el desarrollo de determinados métodos de análisis como la regresión logística binaria (RLB). Esta técnica permite hacer cuantificaciones del riesgo de padecer determinado desenlace, crear modelos predictivos de fenómenos complejos, controlar el efecto de posibles variables confusoras y analizar la interacción entre diferentes covariables, siempre que se trate de un desenlace dicotómico.
Hosmer y Lemeshow, ofrecen los fundamentos y las diversas posibilidades que brinda esta técnica a través de ejemplos, Silva, también expone su amplio y creciente empleo en los trabajos publicados en revistas biomédicas de alto impacto, llegando a ser el modelo de análisis multivariado más utilizado en la literatura médica desde mediados del siglo XX hasta la actualidad. 1
El análisis estadístico implicativo, conocido por la sigla ASI de Analyse Statistique Implicative del idioma francés donde se originó, es una herramienta de la minería de datos basada en las técnicas estadísticas multivariadas, la teoría de la cuasi-implicación, la inteligencia artificial y el álgebra booleana, para modelar la cuasi-implicación entre los sucesos y variables de un conjunto de datos. (2,3)
Esta técnica surgió para solucionar problemas de la Didáctica de las matemáticas y fue creada por el francés Régis Gras, profesor emérito de la Universidad de Nantes, Francia, quien comenzó sus trabajos en este campo en 1980, y desde entonces ha venido estudiando el fenómeno de la creación de reglas inductivas no simétricas y de la cuantificación de la probabilidad de que se presente una cierta característica b si se ha observado otra característica a en la población. El ASI contempla la estructuración de datos, interrelacionando sujetos y variables, la extracción de reglas inductivas entre las variables y, a partir de la contingencia de estas reglas, la explicación y en consecuencia una determinada previsión en distintos campos del saber. (4
Varias investigaciones han validado la efectividad del ASI en la identificación de factores pronósticos o de riesgo utilizando como estándar de oro la RLB al ser aplicadas en estudios observacionales de tipo caso control, clásicos o anidados en una cohorte. Para validar la capacidad diagnóstica del ASI se han estimado en cada uno de estos estudios indicadores como: sensibilidad, especificidad, valores predictivos, razones de verosimilitud, entre otros. (5-8
El objetivo de este trabajo es establecer una comparación entre la RLB y el ASI, a fin de determinar similitudes y diferencias entre ambas y poder decidir en qué medidas emplear una o ambas técnicas en los estudios para la identificación de factores pronósticos o de riesgo. Para lograr este propósito se llevó a cabo una exhaustiva revisión de la literatura en las bases de datos biomédicas de la Internet y de los resultados del conjunto de investigaciones, antes mencionadas, en las cuales se aplican de forma simultánea ambas técnicas al mismo conjunto de datos para verificar las características a comparar en la práctica. Se definieron como patrones de comparación los siguientes aspectos:
Formulación teórica
Tipo de variables para emplear la técnica
Cantidad y requisitos que deben satisfacer las variables para aplicarse las técnicas
Tratamiento de las variables previo al análisis
Tamaño de la muestra
Multicolinealidad y monotonía
Características de la identificación de las relaciones entre variables
Indicadores básicos estimados en el análisis
Característica de los índices para establecer las relaciones entre variables
Nivel de confianza establecido por el investigador
Influencia de las observaciones raras en la validez de los resultados
Identificación de confusores
Procesadores automatizados para la aplicación de la técnica
Métodos de presentación de los resultados
Formulación teórica
El modelo de RLB múltiple, que expresa la probabilidad de que ocurra un evento en función de ciertas variables, viene dado a través de la expresión:
Donde p representa la probabilidad de ocurrencia del evento o desenlace dicotómico estudiado, Y es la variable dependiente (desenlace),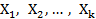 
son las covariables y 
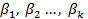son los coeficientes de regresión asociados a cada covariable.1
Algunos autores como Silva, 2 y Aguayo, (13 se refieren al modelo de regresión logística mediante una expresión equivalente a la anterior:
Si la probabilidad (p) se divide por su complementario (1-p), se obtiene el odds, el cual cuantifica cuanto más probable es tener el desenlace que no tenerlo, y viene dado por la expresión:
Empleando la transformación logit se obtiene un modelo lineal que permite un mejor manejo de los datos e interpretación de los resultados, quedando la expresión siguiente:
La estimación de los parámetros (coeficientes de regresión) del modelo se realiza por un proceso de máxima verosimilitud a través del algoritmo iterativo de Newton-Raphson. (14
El modelo obtenido debe cumplir con dos aspectos: el principio de parsimonia, que aboga por la menor cantidad de variables que expliquen los datos, y que sea clínicamente congruente e interpretable.
Existen varios métodos para la selección de las variables que conformarán el modelo y una vez obtenido se evaluará su ajuste a los datos mediante pruebas estadísticas que determinan si las covariables se asocian con el desenlace de interés más de lo que podría esperarse solo por azar (lo que corresponde a un valor de p < 0,05 si el investigador ha fijado un nivel de significación del 5%). Entre estas pruebas se pueden citar las pruebas G de razón de verosimilitud, ómnibus, de Wald y Score, para contrastar la bondad de ajuste en cada paso y la prueba de bondad de ajuste de Hosmer y Lemeshow, la lejanía o desvianza, el coeficiente R2 y otras pseudo-R2 como la de Cox y Snell, la de Nagelkerke y la de McFadden, que se usan para contrastar la bondad de ajuste desde un punto de vista global. (9-13
Aunque el modelo ajuste bien se debe hacer un diagnóstico posterior para corroborar el cumplimiento de los supuestos, si otra función (no logística) describe mejor los datos, si existen valores raros o con excesiva influencia en la estimación de los parámetros del modelo. Este diagnóstico se realiza mediante: el análisis de los residuos del modelo que pueden ser de tres tipos: estandarizados, estudentizados y de desviación y las medidas de influencia que cuantifican la influencia que cada observación ejerce sobre la estimación del vector de parámetros o sobre las predicciones, como son la medida de apalancamiento (Leverage), la distancia de Cook y los Dfbeta. (14,15
La curva de características operativas del receptor (curva COR o en inglés ROC) también permite cuantificar la capacidad del modelo para clasificar o pronosticar. (16)
En el ASI la validez de la regla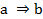 
(donde 
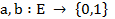son dos variables binarias representando dos características objeto de estudio y E es el conjunto de los sujetos o individuos) depende de la probabilidad o fuerza de la cuasi-implicación, que se determina al comparar el número de contraejemplos presentes que invalidan dicha regla con los que aparecerían bajo una ausencia de relación estadística.
El ASI consta de tres procedimientos: la implicación, la cohesión y la similaridad. Para definirlos se parte de considerar 
, conjuntos de individuos que poseen la característica a y b, respectivamente, siendo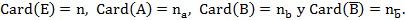 
La implicación
En la implicación se destacan tres conceptos básicos: intensidad implicativa, índice de implicación e índice de implicación-inclusión.
La intensidad implicativa, la cual se denota por
es una medida probabilística de la validez de la regla 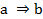y se calcula a partir de la siguiente expresión:
Donde n representa el número de individuos o sujetos objeto de estudio,
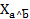representa la cantidad de contraejemplos esperados y 
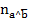los contraejemplos observados. La decisión de aceptar o no la regla está en función del nivel de significación 
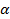o su complemento, el nivel de confianza
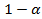elegido por el investigador y se dirá que la regla 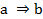es admisible para un 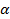dado si
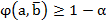, o sí 
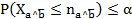.El índice de implicación,
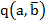es un indicador de la no implicación de a sobre b. Es no simétrico y no coincide con el coeficiente de correlación u otros índices simétricos que miden asociación. Viene dado por la expresión: 
El índice de implicación-inclusión o de implicación entrópica,
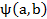es la versión entrópica del índice de implicación y supera la poca discriminación de este en muestras grandes. Este índice mide la calidad inductiva de a sobre b y de su contra recíproco (no b sobre no a) y viene dada por la expresión:
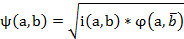Donde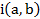 
es el índice de inclusión de A, soporte de a, en B, soporte de b.
La cohesión
La cohesión permite estructurar el conocimiento en forma de reglas y meta reglas y superar la simple articulación de las partes de una tipología clásica, a fin de alcanzar un todo significativo al ser de carácter no lineal, asimétrico, jerárquico y dinámico. Las reglas y meta reglas que surgen se puede presentar en tres esquemas:
, donde 
, que se interpreta como que c es consecuencia de la regla R.
, donde 
, que se interpreta como que a se dedujo de la regla R o que la regla R es consecuencia de a.
, donde 
y 
, que se interpreta como que 
se dedujo de la regla 
o que la regla es consecuencia de .
A partir de la entropía (H), la cual permite dar cuenta del desorden entre las variables, se define el índice de cohesión entre dos variables a y b, el cual mide la fuerza de la consistencia de las variables involucradas en la clase creada a través de la siguiente expresión:
Siendo 
.
Para la formación de las reglas y meta reglas se sigue el siguiente procedimiento: en el primer paso o nivel de la jerarquía se calcula el índice de cohesión entre cada par de variables (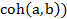
. En cada paso siguiente se calcula el índice de cohesión entre cada par (ordenado) de clases y se forma una nueva clase que reúne (y remplaza) a las dos anteriores y así sucesivamente. Intuitivamente, la cohesión mide el desequilibrio de las frecuencias de los eventos 
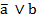y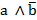 
a favor del primero.
En la cohesión, Gras y Kuntz, 17) plantean que, las reglas y meta reglas elaboradas harán referencia a variables que se estructurarán en clases ajustadas y orientadas de manera ascendente. Una regla entre clases de variables solo tiene sentido bajo la condición de que dentro de cada clase de variables, cuya relación se examina, exista una cierta "cohesión" entre las variables que la constituyen; esto debe hacerse respetando el orden instituido en la clase, para ello el "flujo" implicativo de una clase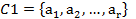 
de r características sobre una clase 
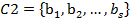de s características estará reforzado con un "flujo" interno en 
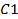y a la vez, reforzará el "flujo" interno en 
.
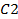La cohesión de la clase ordenada de variables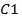 
es definida como la media geométrica de las cohesiones de los pares de variables que la conforman, esto es:
La similaridad
La similaridad es una medida de correspondencia o semejanza entre los objetos que van a ser agrupados. A diferencia de los métodos de clasificación usualmente empleados, en el ASI se emplea el índice de similaridad de Lerman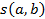 
, que se calcula como la probabilidad de que el número observado de copresencias entre dos variables sea mayor o igual que el de las copresencias esperadas por el azar, esto es:
Donde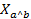 
representa la variable aleatoria asociada con el número de ejemplos en el modelo aleatorio asumido, y 
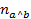, es el valor observado (copresencias de a y b) de los ejemplos en la regla 
.
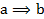Al igual que como se procede con el índice de cohesión para formar la jerarquía, se procede con el índice de similaridad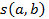 
para formar conglomerados con una jerarquía ascendente atendiendo a su semejanza, al calcular este índice para cada par de variables o clases de variables que se vayan formando.
Además de los procedimientos antes descritos, el ASI permite cuantificar el aporte de cada individuo en la formación de las estructuras que se obtienen a partir de los índices de cohesión y de similaridad, para lo cual emplea la contribución o la tipicalidad de cada sujeto. La tipicalidad es un índice porcentual que mide cómo se comporta un individuo en relación a la regla o a la clase, llamando sujeto típico a aquél que verifica todas las implicaciones (similaridades) que poseen mayor intensidad de implicación (índice de similaridad) en la formación de las reglas (clases). La contribución cuantifica el aporte de un determinado individuo en la formación de la regla o de la clase. Por ejemplo, si una regla a ⇒ b posee una intensidad implicativa de 0.7, entonces los individuos más contributivos son los que tienen el valor 1 para las variables a y b.
Tipos de variables para emplear la técnica
La RLB se puede aplicar siempre que exista una variable dependiente representando el desenlace, que es dicotómico (caso o control) y las covariables se conforman con las supuestas causas que influyen en el desenlace, solas o combinadas si se sabe que existe efecto de interacción entre ellas. Las covariables pueden ser medidas en cualquier escala inicialmente y luego se transformarán según lo requiera el análisis.
El ASI admite el tratamiento de variables medidas en cualquier escala, binarias, modales, frecuenciales, de intervalo y hasta difusas, sin distinción entre variables dependientes e independientes o covariables. En este trabajo solo se analizará el caso binario. (17
Un aspecto interesante de esta técnica es que, tanto en el análisis cohesitivo como en el de similaridad, las variables pueden ser analizadas como variables principales o suplementarias. La variable suplementaria es extrínseca al estudio, no interviene directamente en las relaciones entre las variables principales, pero permite esclarecer la importancia o la superfluidad de estas categorías en la formación de las reglas o meta reglas. Generalmente se emplean variables modales como variables suplementarias. Esta posibilidad puede ser aprovechada en los estudios de causalidad en biomedicina para determinar cuánto contribuyen los casos o los controles a la formación de las relaciones entre las variables, empleando las variables que representan el desenlace como suplementarias.
Número y requisitos de las variables para el análisis
El número de variables en la RLB está en relación con el tamaño de muestra, no obstante, por el principio de parsimonia que debe cumplir el modelo hay que tratar de explicar los datos con el menor número de variables posible. Más importante que el número de variables son los requisitos que deben cumplir las variables a incluir o excluir del modelo. Para incluir las covariables se deben tener en cuenta todos los aspectos relacionados con la pregunta de investigación y cualquier variable que potencialmente pueda afectar la relación entre las covariables y el desenlace (variables confusoras y modificadoras del efecto).
Previo a la construcción del modelo se deben aplicar técnicas bivariadas para estudiar las posibles asociaciones entre las covariables y la variable dependiente.
Se deben incluir como covariables aquellas que: en el análisis bivariado previo demostraron una relación "suficiente" (la literatura sugiere emplear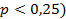 
con la variable dependiente, ya que a pesar de existir una débil asociación en solitario pueden ser fuertes predictoras al analizarlas en conjunto con el resto de las covariables, que sean clínicamente importantes, con independencia de si se demostró la significación estadística de la asociación, y por teoría o investigaciones previas se consideren variables confusoras.18
Las covariables a excluir del análisis son las que: definitivamente no están en la vía causal que se está analizando, las que sean redundantes o estrechamente relacionadas, para evitar la multicolinealidad, o las que sean intervinientes (se encuentran en la vía causal del desenlace, pero son desencadenadas o causadas directamente por el mismo factor de riesgo o pronóstico en estudio, por lo que perdería valor la asociación del factor con el desenlace). (18
En el ASI no hay restricción en cuanto al número de variables o requisitos que deben cumplir para entrar o salir del análisis. Este análisis aportaría un nuevo criterio para apoyar la difícil decisión de cual variable incluir o no en el modelo de RLB por lo que se sugiere se realice previo a la RLB, como una técnica gráfica para el análisis exploratorio de datos.
Tratamiento de las variables previo al análisis
En la RLB la variable dependiente es dicotómica y las covariables pueden ser de cualquier tipo. Las covariables dicotómicas tienen ventaja con respecto a otros tipos de variables, ya que pueden ser analizadas sin necesidad de ninguna transformación, codificadas como 1 (presencia de la característica) y 0 (ausencia de la misma).
Con los otros tipos de covariables es necesario efectuar transformaciones específicas para poder analizarlas. Las politómicas deben convertirse en múltiples variables dicotómicas, llamadas variables dummy o indicadoras. (19) En este proceso de transformación se debe especificar la categoría de referencia contra la cual se comparan todas las otras alternativas.
Para las variables ordinales se deben crear también variables dummy, con la diferencia que en estas sí hay un orden jerárquico entre las diversas categorías.
Para las variables continuas, el modelo multivariado asume que cada cambio de una unidad, en cualquier punto de la escala de la covariable, tiene un cambio de igual magnitud en la variable dependiente (asunción de linealidad). (20) Por lo que se recomienda, cuando las variaciones entre una unidad y otra no son importantes, discretizar la variable.
El ASI, al contextualizarse a la investigación médica de causalidad, a sugerencia de estas autoras, requiere cambios importantes en las variables. En este trabajo solo se analiza el caso en que todas las variables son binarias. Antes de efectuar el análisis, se deberán efectuar transformaciones en la variable dependiente y en las covariables que sean más que dicotómicas. La variable dependiente, de respuesta o desenlace, que tradicionalmente es única con dos categorías, se duplicará contando para el análisis con dos variables dependientes binarias que representen el desenlace peor y mejor, respectivamente.
Así, por ejemplo, en los estudios para la identificación de factores de riesgo se crearán dos variables, “enfermo” y “no enfermo”, y para la identificación de factores pronóstico una variable para el desenlace favorable y otra para el desfavorable, que según el tipo de desenlace que se escoja podría ser “vivo” y “fallecido” o “complicado” y “no complicado”, etc.
Cada variable creada se codificará con el valor 1 si el individuo analizado posee la característica de interés y con el 0 en caso contrario. Por ejemplo, la variable “fallecido” toma el valor 1 si el individuo ha fallecido y 0 en caso contrario y la variable “vivo” toma el valor 1 si está vivo y 0 en caso contrario.
Esta duplicación se sustenta por el hecho de que el algoritmo empleado en el procesamiento de estos datos sólo analiza la variable codificada con 1, por ejemplo, en el caso de la identificación de factores pronósticos de mortalidad si se declarase una sola variable “estado”, donde se representase el fallecido con 1 y el vivo con 0, nunca sería posible analizar las relaciones de causalidad asociadas al estado vivo, es decir identificar los factores de buen pronóstico que pudieran existir.
Con respecto a las variables independientes o covariables que sean politómicas, se sugiere dicotomizarlas para ganar en eficiencia, tal como ocurre en la regresión, aun cuando parezca que se pierde en información. Este proceso, el cual permitirá visualizar mejor el cambio de una categoría a otra y facilitará su interpretación, se puede realizar de dos formas:
Creando tantas variables nuevas como categorías posean, por ejemplo, estado civil, que habitualmente es una variable con cuatro categorías, se convierte en cuatro variables dicotómicas: casado, soltero, divorciado y viudo, con las categorías si o no. Esto es algo semejante a la creación de variables sintéticas o dummy que se hace en la regresión logística.
Creando dos variables, en las cuales se agrupen, siempre que sea posible, varias categorías, por ejemplo, en caso que tuviera sentido, estado civil se codificaría con 1 para casados y viudos y con 0 para solteros y divorciados.
En el caso de las covariables cuantitativas, estas se transformarán en categóricas, preferiblemente con dos categorías, considerando la de peor y mejor pronóstico para los estudios de identificación de factores pronósticos, o la que pudiera constituir un factor de riesgo o un factor protector, en los casos de identificación de factores de riesgo, siempre codificando con 1 la peor situación y con 0 el caso contrario.
Este proceso de dicotomizar consiste en buscar un punto de corte apropiado en el recorrido de la variable, lo cual es posible hacer de diferentes formas:
A partir de una hipótesis teórica que pueda operacionalizarse en el estudio y que tenga cierto sentido explorar; por ejemplo, teniendo en cuenta que se conoce de otro estudio que las edades de peor pronóstico son las mayores de 50, en un estudio de factores pronósticos podría transformarse la variable edad a dos categorías mayores de 50 años y menores o iguales de 50 años.
Si no hay una hipótesis previa es posible emplear la mediana, que permite agrupar los individuos, previamente ordenados según el valor de la variable, en dos grupos de igual tamaño.
Establecer el punto de corte arbitrariamente, lo cual es lo menos recomendable.
Emplear la estrategia propuesta por Molinero 16 conformada por los siguientes pasos: se toman dos percentiles
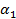y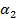 
cercanos al 75 percentil por ambos lados, si se supone que los valores más altos de la variable son los que determinan el peor desenlace; se recodifica la variable en dos nuevas variables dicotómicas asociadas a cada uno de sus percentiles, asignándole la categoría 0 a los valores menores que 
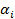y la categoría 1 para los valores mayores o iguales a 
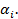; se conforman dos tablas de contingencia de 2X2 para cada una de las variables dicotómicas, donde se asocian con la variable dependiente y se calcula el valor del estadígrafo chi cuadrado de Pearson en ambas; el mejor punto de corte, hasta el momento, se corresponderá con el mayor valor de los dos estadígrafos calculados (mínimo valor de p); luego se repite el proceso empleando dos percentiles cercanos al percentil que arrojó el mayor valor del estadígrafo hasta el momento (mínimo valor de p) y así se reitera el proceso hasta ir acercándose y finalmente encontrar el mayor valor de todos.
Lo recomendado es siempre consultar la literatura disponible, así como la opinión de expertos en el tema para hacer corresponder la relevancia clínica con la estadística.
Además de la codificación en 0 y 1, como en los estudios habituales, se sugiere que se exponga siempre en la operacionalización de las variables el nombre con el cual se procesarán estas en la base de datos, ya que a través de este nombre se visualizan en los gráficos, aspecto muy importante para poder comprender las relaciones que se establecen e interpretar los gráficos obtenidos. Se deben emplear nombres que identifiquen por si solos la variable de que se trata y que no sean muy largos, sobre todo si se trabaja con muchas variables, para facilitar la comprensión del gráfico.
Tamaño de la muestra
En principio, se puede calcular el tamaño de muestra por la fórmula para los casos y controles balanceado o no balanceado, según el diseño. (21
La RLB requiere un tamaño de muestra grande, de al menos 10 sujetos por cada variable independiente para lograr estimaciones adecuadas. Existen varios criterios a tener en cuenta ya que si la muestra no es suficientemente grande implicará errores estándar grandes y la estimación de coeficientes falsamente elevados (sobreajuste). Al respecto, en la literatura se encuentran varios criterios: Hosmer y Lemeshow (1980) recomiendan más de 400 unidades de análisis, Freeman (1987) sugiere emplear diez veces el número de variables independientes a estimar más uno, De Maris (1992) sugiere 15 casos por variable, Peduzzi (1996) sugiere por cada covariable contar al menos 10 casos por cada evento de la variable dependiente con menor representación, Long (1997) sugiere incrementarlo a 100. Estas autoras recomiendan seguir el criterio de Peduzzi, que es el más generalizado. 22
Del ASI no se reportan criterios restrictivos en cuanto al tamaño de muestra a emplear en el análisis. Se puede trabajar con muestras pequeñas o extremadamente grandes. En dependencia del tamaño de muestra se seleccionará una distribución u otra a la hora de estimar los índices en el análisis. La distribución que siguen estas variables aleatorias depende del patrón asumido para seleccionar los subconjuntos, pudiendo ser la hipergeométrica (cuando la población es finita y la muestra es de tamaño fijo), binomial (población infinita y tamaño de muestra fijo) o Poisson (población infinita y tamaño de muestra aleatorio). Bodín, (18 detalla los modelos y pruebas de hipótesis para cada distribución. El trabajo con muestras grandes requiere que el investigador elija el enfoque entrópico a la hora de llevar a cabo el análisis implicativo.
Multicolinealidad y monotonía
La RLB requiere del cumplimiento de ciertos supuestos, así que antes de construir el modelo de la RLB es preciso tener en cuenta algunas precauciones para que el mismo tenga sentido, entre ellas: el tamaño de muestra, el tratamiento de las covariables, los criterios de inclusión y exclusión de estas, la multicolinealidad y la monotonía.
De los primeros requerimientos se habló en los acápites anteriores, solo se comentan a continuación los dos últimos. Se debe evitar la multicolinealidad ya que genera varianzas y covarianzas extremadamente grandes con lo cual los intervalos de confianza de los coeficientes serán muy amplios. Además, aparecen como no significativas variables que a priori se esperaría que lo fuesen. (23)
Para el diagnóstico de la multicolinealidad se puede emplear el factor de inflación de la varianza, el cual mide el incremento que se produce en la varianza de los estimadores de los coeficientes de regresión al comparar dicha varianza con la que deberían tener si las covariables fuesen incorrelacionadas. También es posible usar los autovalores o el índice de condición. (18
En presencia de multicolinealidad se tienen las siguientes opciones: aumentar el tamaño de muestra, omitir la covariable que es teóricamente menos importante, la que presenta más valores faltantes o de alguna manera es menos satisfactoria para el análisis o transformar las covariables: centrando con respecto a la media, estandarizando, con escalas más elaboradas o creando variables sintéticas mediante un análisis previo de componentes principales. Las opciones 2 y 3 se emplean a riesgo de invalidar la capacidad predictiva del modelo. (16
Otro de los supuestos para que la regresión logística tenga un sentido claro es la existencia de una relación monótona entre las covariables y la probabilidad del evento que se estudia, o sea, debe evitarse que dicha probabilidad aumente para cierto recorrido de valores de la covariable y disminuya para otro rango de valores de esta.
En el ASI no se requiere del cumplimiento de ningún supuesto en especial para que el resultado sea válido.
Características de la identificación de las relaciones entre variables
La RLB identifica solamente aquellas covariables con una fuerte asociación con la variable dependiente o desenlace y no permite visualizar las relaciones existentes entre el conjunto de covariables estudiadas. El hecho de considerar la no existencia de multicolinealidad como supuesto básico conlleva a excluir del modelo covariables correlacionadas, por lo que tampoco sería posible identificar la relación de la variable dependiente con estas variables excluidas.
Dunkler,20 plantea que el procedimiento paso a paso hacia detrás puede excluir confusores del modelo o dejar falsos confusores, dado que la selección se realiza a través de algoritmos basados en el valor p (índice decreciente de la fiabilidad de un resultado), sin la opinión del investigador.
El ASI permite estimar la relación existente entre todas las variables con diferentes intensidades de implicación. A medida que el investigador selecciona una intensidad de implicación menor aparecen nuevas variables y nuevas relaciones entre ellas.
Indicadores básicos estimados en el análisis
La RLB estima como indicadores básicos los odds ratio o razón de probabilidades, dados por la exponencial del coeficiente de regresión (β) que acompaña a cada covariable, el p valor para probar la significación de estos y sus intervalos de confianza.
Proporciona, además, otros indicadores que complementan el análisis y permiten decidir sobre la bondad de ajuste y diagnóstico del modelo, antes comentados.
El ASI aporta una información diferente al estimar tres índices básicos: de similaridad, de cohesión y de implicación. Además, muestra indicadores como: la frecuencia absoluta de ocurrencia de cada variable, su media y desviación estándar, la frecuencia de ocurrencia de cada pareja de variables que se pueden formar y sus coeficientes de correlación.
Característica de los índices para establecer las relaciones entre variables
La RLB exige una relación lineal entre el logit de la probabilidad del suceso de interés y las covariables que conlleva a transformaciones para lograrlo.
En el ASI todos los índices son asimétricos, no lineales, en correspondencia con la complejidad de los procesos naturales y sociales como el de salud-enfermedad.
Nivel de confianza establecido por el investigador
La RLB trabaja con un solo nivel de confianza, habitualmente el 95%, con el cual se estima el intervalo de confianza de los odds ratio. Este intervalo se hace más amplio, si sube el nivel de confianza o más estrecho, si baja, manteniendo las mismas covariables y el mismo valor de odds ratio para cada covariable.
En el ASI el nivel de confianza se establece a partir de la intensidad implicativa. El mismo permite el manejo de cuatro niveles de intensidad implicativa a la vez, que se modifican según el criterio del investigador y que permiten un análisis más amplio y una interpretación más completa del fenómeno de la causalidad. A medida que el investigador decide disminuir este nivel pueden aparecer nuevas relaciones y/o nuevas variables se incluyen en la trama causal.
Influencia de las observaciones raras en la validez de los resultados
Algunas observaciones “raras” que constituyen valores extremos pudieran tener una influencia exagerada en las estimaciones de los parámetros del modelo logístico, lo cual lo invalidaría. En estos casos es conveniente realizar siempre un análisis exploratorio para identificar casos que pudieran afectar las estimaciones, inclusive repetir el análisis con y sin el caso para apreciar los cambios.
El ASI por restringirse a sucesos frecuentes desoye lo trivial, por lo que no se ven afectados los resultados.
Identificación de confusores
La RBL a través del método de selección paso a paso asegura la selección de los confusores, aunque algunos autores plantean que esta selección a partir de algoritmos basados en el valor p puede excluir confusores importantes o dejar erróneamente variables clasificadas como confusores. (18) El modelo causal estructural constituye una alternativa a los modelos clásicos de regresión para identificar confusores. (3
En el ASI es posible identificar posibles confusores por la similitud del grafo implicativo con el diagrama causal denominado grafo acíclico dirigido (DAG del inglés Directed Acyclic Graphs) empleando los mismos métodos propuestos para estos diagramas cuya teoría ha sido abordada ampliamente y aplicada por muchos autores. (2
Procesadores automatizados para la aplicación de la técnica
La técnica está implementada en procesadores estadísticos de propósito general como el SPSS (Statistical Package for the Social Science), el Statistica, Minitat, SYSTAT, SAS, STATA, entre muchos otros. También existen varios programas específicos, por ejemplo, de autores cubanos como Luis Carlos Silva y Humberto Fariñas, quienes sobre los años 90 confeccionaron el RELODI y el RELOPO.
En el ASI la herramienta informática que posibilitó este análisis en un principio fue el software específico designado por el acrónimo CHIC (del francés: Classification Hiérarchique Implicative et Cohésitive que significa Clasificación Jerárquica, Implicativa y Cohesitiva), el cual proporciona de forma rápida, gran cantidad de cálculos y gráficos. Su programación fue iniciada por Régis Gras y retomada por autores como Saddo Ag Almouloud, Harrison Ratsimba-Rajohn y Raphaël Couturier, (7) quien, además, implementó un paquete en R con estas mismas posibilidades de cálculo y representaciones gráficas denominado RCHIC. En Santiago de Cuba se creó el SIASI que ha sido validado en diferentes estudios. (4
Métodos de presentación de los resultados
La RLB muestra múltiples tablas, de resumen del modelo, de clasificación, entre otras; siendo la más importante la tabla de los odds ratio dada por la exponencial de β y sus intervalos de confianza. No se emplean gráficos de presentación propiamente dichos.
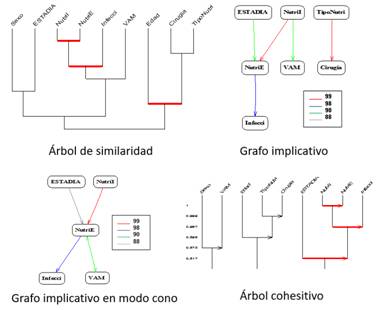
En el ASI los resultados se presentan en tres gráficos que ilustran mejor los resultados y facilitan la interpretación de los mismos: arboles de similaridad, de cohesión y el grafo implicativo, que puede ser general y también en modo cono según decida el investigador. (figura) Estas autoras consideran apropiado formar dos grafos en modo cono para la identificación de factores de riesgo o pronóstico ubicando en cada cono el peor y mejor desenlace.
También se muestran múltiples cuadros donde constan las frecuencias absolutas de ocurrencia de cada variable, sus medias y desviaciones estándares, las frecuencias de ocurrencias de cada par de variables que se pueden formar, así como sus coeficientes de correlación, los índices de similaridad, de cohesión implicativa y de implicación inclusión, las tipicalidades y contribuciones de los individuos.
Tanto en el árbol cohesitivo como en el de similaridad se pueden representar los nodos significativos (marcados en rojo en los árboles de la figura), los cuales representan los nodos correspondientes a una clasificación compatible lo mejor posible con los valores y la calidad de los valores de implicación y de cohesión, en el árbol cohesitivo, y de similaridad para el árbol de similaridad. Los nodos internos del árbol dirigido representan la jerarquía dirigida y describen relaciones implicativas complejas entre el conjunto de variables estudiadas llamadas R-reglas.
Conclusiones
A partir de los catorce patrones de comparación analizados se pudo visualizar que a pesar de tener el mismo propósito, ambas técnicas arriban a resultados diferentes, con ciertas ventajas del ASI sobre la RLB en cuanto a los requerimientos para su ejecución y concluir que ninguna es mejor, sino que ambas se complementan, por lo que su empleo simultáneo en investigaciones clínico-epidemiológicas para la identificación de factores pronósticos o de riesgo a partir de diseños observacionales enriquecería los resultados de estos estudios y su interpretación. Se sugiere emplear primero el ASI, cuyas salidas ayudarían en el proceso de decisión de cuáles variables serán incluidas en el modelo de RLB.
