Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Cubana de Higiene y Epidemiología
versión On-line ISSN 1561-3003
Rev Cubana Hig Epidemiol v.38 n.3 Ciudad de la Habana sep.-dic. 2000
ARTÍCULOS ORIGINALES
Ministerio de Salud Pública. Área de Higiene y EpidemiologíaMétodos para la vigilancia de eventos en salud
Dra. Gisele Coutin Marie,1 Lic. Jorge Borges Soria,2 Dr. Ricardo Batista Moliner,3 Dr. Andrés Zambrano Cárdenas 4 y Dr. Pablo Feal Cañizares 5.
RESUMEN
Uno de los objetivos fundamentales del trabajo en las unidades de análisis y tendencias es el perfeccionar los métodos de vigilancia utilizados en el país de manera que se garantice la detección oportuna de cualquier comportamiento que se desvíe de lo normal esperado para los eventos de salud de nuestro interés. Durante los 5 años de funcionamiento de nuestras unidades hemos utilizado diversos métodos para lograr este propósito, tomando en consideración los avances en la materia en el ámbito internacional. Recientemente hemos comenzado a emplear 2 nuevos métodos. El primero de ellos está dedicado a la comparación de lo observado con el comportamiento histórico obtenido mediante un sencillo procedimiento de cálculo, mientras que el segundo está concebido para el procesamiento de los eventos de muy baja incidencia, los cuales resultan difíciles de tratar con cualquiera de los procedimientos tradicionales, este último emplea la distribución de probabilidades Poisson. Con ambos métodos se han obtenido buenos resultados pues permiten la detección de desviaciones del comportamiento habitual con bastante exactitud y se recomendó su uso en nuestras unidades provinciales y municipales. Descriptores DeCS: VIGILANCIA DE LA POBLACIÓN; TÉCNICAS INVESTIGATIVAS.
Uno de los principales problemas que afronta la vigilancia en salud no sólo es el de poder detectar variaciones significativas en el patrón de comportamiento habitual de las enfermedades, sino, hacerlo rápida y eficazmente. Es por ello que la detección de patrones inusuales en los datos de vigilancia rutinarios en ocasiones representa una dificultad de envergadura considerable para los investigadores.1-3
Dado que uno de los fundamentos de la Epidemiología es estudiar las diferencias entre los eventos observados y los esperados según la experiencia previa, la mayoría de los métodos más utilizados descansan en la comparación de lo observado en un período determinado, con lo hipotéticamente esperado para ese lapso de tiempo; por lo cual es aconsejable el empleo y diseminación de las técnicas que con la mayor prontitud alerten acerca del posible comportamiento diferenciado. No obstante, es conveniente tener en cuenta que no debe utilizarse un método único para pretender detectar con éste todo tipo de desviaciones de lo considerado como normal, lo ideal es disponer de varios procedimientos para comparar los resultados.4
Por este motivo en la Unidad de Análisis y Tendencias en Salud (UATS) se han utilizado diferentes técnicas entre las cuales se pueden citar los métodos tradicionales de análisis del canal endémico de las enfermedades, el estudio de las tendencias de las mismas, la elaboración de pronósticos e intervalos de predicción para ellos con las técnicas clásicas y con modelos estocásticos, entre estos los más utilizados han sido los modelos ARIMA o modelos autorregresivos de medias móviles.5,6 También se utiliza cada semana un gráfico donde se compara el incremento o decremento acumulado con relación a igual período del año anterior, que ha resultado ser de gran utilidad. Recientemente se han comenzado a emplear 2 nuevos métodos con el propósito de perfeccionar nuestra vigilancia. Este trabajo consiste en la descripción de los dos métodos, su implementación y los resultados obtenidos con su aplicación en el país.
Método para comparar el comportamiento observado en relación con el comportamiento histórico
El método que hemos empleado en nuestra unidad desde hace varios meses es similar al desarrollado por Donna Stroup y otros7,8 y consiste en la comparación del valor observado para un evento determinado en un momento (número de casos reportados en un período: semana o mes) con una línea de base que se utiliza como referencia y que está conformada por una base de datos que incluye la información de los casos de esa enfermedad reportados en 15 intervalos de tiempo pertenecientes a 5 ó más años anteriores. Estos intervalos comprenden las observaciones del período inmediato anterior, del período central (correspondiente a un momento de tiempo similar al actual) y la inmediatamente posterior. Un esquema de lo anteriormente explicado se muestra en la tabla 1.
| | | | |
| Año actual | | ||
| Año 1 | | | |
| Año 2 | | | |
| Año 3 | | | |
| Año 4 | | | |
| Año 5 | | | |
El período central es representado por un conjunto de 4 semanas que incluye la semana que interesa evaluar en la actualidad y las 3 inmediatamente anteriores, esto se realiza con el propósito de evitar las fluctuaciones que puedan producirse, debido más a irregularidades en los mecanismos de notificación que a verdaderas variaciones en la incidencia de la enfermedad. La decisión de utilizar 5 años obedeció a las características de la información disponible, pues cuando se elaboraron las bases de datos no disponían de datos uniformes para todas las enfermedades, ya que todas las estudiadas no habían comenzado a notificarse en el mismo tiempo. No obstante, esta característica es opcional pues posteriormente implementaron este gráfico para grupos de años de referencia mayores, hasta 7 ó 10 años.7
En la tabla 2 se muestra un ejemplo de cómo quedan conformados los diferentes períodos de la línea de base cuando se desea comparar lo acontecido en la semana 10 de 1999 con la media histórica representada por los períodos de los 5 años anteriores (1994-1998). Observe que el período actual se representa con la semana objeto de nuestro interés y las 3 semanas que le anteceden con el propósito de atenuar las deficiencias en los reportes de casos, pues puede suceder que en determinada semana no se reporten todos los casos ocurridos y que parte de ellos se informen en la semana siguiente produciendo un pico que no representa la verdadera realidad.
TABLA 2. Esquema de los períodos analizados por el método
Período actual
| Años | | | Semanas 11-14 |
| 1998 | | | |
| 1997 | | | |
| 1996 | | | |
| 1995 | | | |
| 1994 | | | |
Para la construcción de este modelo se asumió que en ausencia de aberraciones de cualquier tipo, las Xi (conjunto de casos reportados en el período) constituyen variables aleatorias independientes que poseen la misma distribución, lo cual resulta ventajoso para poder emplear la teoría normal en la obtención de intervalos de confianza. Los intervalos de confianza calculados en torno a los valores esperados permiten determinar si la enfermedad se mantiene dentro de, lo esperado o si se "sale" de estos límites. Es decir que la comparación del período actual con este marco de referencia, dado por el conjunto de datos de períodos anteriores permite responder a la interrogante de si el número de casos observados este año resulta diferente de los años anteriores.
Ahora bien, para representar el valor esperado en el momento analizado, se decidió utilizar la media aritmética del número de casos de los 15 períodos de la línea de base, aun cuando se sabe que dadas las características muy particulares de esta medida de tendencia central no resulta ser la mejor candidata para estos fines pues se ve afectada por los valores extremos, no obstante, la necesidad de utilizar la teoría de la distribución normal obliga a ello. Sin embargo, esto hace que el método no sea muy recomendable cuando entre los años utilizados para la línea de referencia aparecen valores epidémicos, sin embargo, si esos valores pueden ser tratados por cualquiera de las técnicas para la sustitución de valores aberrantes, el método conserva todas sus bondades.
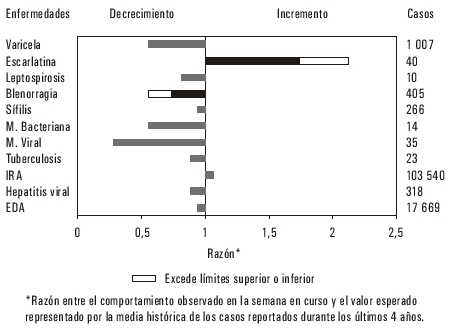
Para obtener los intervalos de confianza se definieron los límites históricos de cada enfermedad como: 1 ± 2 * s x, donde la unidad representa la igualdad entre casos observados y esperados y el cociente entre la desviación estándar y la media no es más que el coeficiente de variación, medida de dispersión relativa, utilizada en este caso para poder comparar entre sí las dispersiones de varias series de enfermedades en torno a sus medias. En la figura se señalan las desviaciones significativas del comportamiento histórico mediante una barra sombreada con rayas cuya magnitud es igual a la diferencia entre lo actual y lo normal histórico.
Debido a la facilidad que para la interpretación ofrece el gráfico construido sobre un eje de coordenadas centrado en la unidad, pues este es el valor que toma el cociente entre observados y esperados cuando ambos son iguales y dado que los decrecimientos con relación a la media histórica implican valores menores que uno de igual manera que los incrementos conllevan valores mayores que éste, se emplea una escala logarítmica de base 2 y se utilizan las potencias de ese orden en el mismo para representar los aumentos o las disminuciones.
No obstante, este método exige el cumplimiento de algunos requisitos entre los cuales está el que no exista una correlación de primer orden elevada, es decir correlación entre los valores adyacentes de la serie como ocurre en aquellas que tienen una fuerte tendencia lineal. Esto constituye una de las desventajas del método, a la cual habría que añadir también la de que, para los eventos raros, la inestabilidad causada por el escaso número de casos reportados puede provocar que la notificación de casos aislados sea considerada como epidemia. En nuestro caso esto pudiera suceder con el reporte de un caso de rabia o de tétanos, lo cual desde luego debería ser correctamente valorado por los expertos que realizan la vigilancia.
Como cualquier otro medio de diagnóstico utilizado para la vigilancia se requiere que el mismo sea bastante sensible, es decir lo suficientemente capaz de diagnosticar las desviaciones del comportamiento normal que se produzcan. Con los datos ofrecidos por Wharton y otros9 se pudo calcular algunos indicadores para medir su eficiencia, obteniéndose que la sensibilidad fue de 73,68 % y el valor predictivo positivo fue de 51,85. Este valor de la sensibilidad fue considerado bastante alto por ellos quienes hacen responsables de los principales fallos del método en la detección de algunas epidemias el incremento de casos en la línea de referencia y el retraso en el reporte de un número de casos. En cuanto al valor predictivo, esta técnica predijo correctamente el 52 % de las epidemias, mientras que un 48 % de las veces alertó acerca de situaciones supuestamente epidémicas inexistentes, lo cual no constituye un necesario defecto importante de la misma pues resulta relativamente fácil comprobar este diagnóstico mediante los mecanismos establecidos en cualquier unidad de vigilancia. De manera que este método muy suficiente para la vigilancia y detección precoz de comportamientos anormales de las enfermedades.
Sin embargo, el hecho de que la sensibilidad del método se vea afectada por los niveles altos de la línea de referencia, el incremento de la varianza de la misma, la existencia de datos faltantes, el reporte tardío y posterior reparo de los casos, así como el hecho de que el mismo no funciona por igual para todas las enfermedades y resulta desaconsejado para los eventos raros, nos llevan a recomendar la precaución en el empleo de éste y sobre todo la construcción de una buena base de datos revisada y analizada así como a la cuidadosa selección de las enfermedades a incluir en ésta.
Al efectuar los análisis de series de tiempo de las enfermedades de los últimos 10 años, hemos observado que durante los años 1993-1994 se presentaron, en general, comportamientos diferentes a los años anteriores o los subsiguientes en muchas enfermedades, por lo que decidimos utilizar, para construir nuestra línea de referencia, el intervalo de tiempo comprendido entre 1995-1998 para todos los análisis para que nuestras series de datos fueran lo más estables posibles. El ejemplo que presentamos se elaboró para la semana 10 de 1999 (tabla 3) y se mostraron los promedios históricos obtenidos para cada una de las enfermedades, los límites inferiores y superiores del intervalo de confianza construido para ellos así como el número de casos del mes considerado y la razón entre observados y esperados. Observe que la blenorragia ha presentado un decrecimiento que la coloca fuera del limite inferior histórico, mientras que por el contrario la Escarlatina se ha incrementado más allá de su límite histórico superior. Este comportamiento se aprecia mejor al observar la figura 1.
FIG.1 Comparación de la incidencia de enfermedades seleccionadas de la semana con su comportamiento histórico, sem 10, 1999.
| Enfermedades | | | | | |
| EDA | | | | | |
| HEPATITIS VIRAL | | | | | |
| IRA | | | | | |
| TUBERCULOSIS | | | | | |
| ME. VIRAL | | | | | |
| ME. BACTERIANA | | | | | |
| SÍFILIS | | | | | |
| BLENORRAGIA | | | | | |
| LEPTOSPIROSIS | | | | | |
| NEUROPATIA | | | | | |
| ESCARLATINA | | | | | |
| VARICELA | | | | | |
| | ||||
| Municipios | | | | |
| Playa | | | | |
| Plaza | | | | |
| C. Habana | | | | |
| H. Vieja | | | | |
| Regla | | | | |
Como se ha señalado este procedimiento constituye una forma más de analizar el comportamiento de diferentes problemas de salud comparando sus valores actuales y lo ocurrido en períodos anteriores. Sin embargo tiene como deficiencia que no puede utilizarse para analizar eventos de baja incidencia, por lo que se decidió emplear el método que mostramos a continuación.
Método para evaluar eventos de baja incidencia: distribución Poisson
Evaluar el comportamiento de algunos eventos de salud que se presentan con una baja frecuencia resulta de gran importancia en el proceso de vigilancia, sobre todo, con el propósito de identificar los territorios donde el evento considerado exhibe un comportamiento diferente del resto del país de acuerdo con lo esperado para ese problema. Generalmente, se desea saber si esa diferencia es debida a un aumento significativo en el número de casos reportados. Ahora bien, los eventos raros (entiéndase como estos en nuestro caso, aquellos cuya notificación está representada por un número pequeño de casos) resultan en la práctica imposibles de modelar con los modelos clásicos y estocásticos utilizados habitualmente para el tratamiento de las series temporales. Entre otras cosas, ello está determinado por el escaso número de casos que se reportan en un período, notándose con relativa frecuencia que ese número se aproxima a cero y puede incluso ser igual a éste. Es evidente que esta situación es más común en los territorios pequeños, donde incluso, las enfermedades que a escala nacional pueden tener una prevalencia relativamente alta, presentan incidencias muy pequeñas en los períodos generalmente analizados (semanas, meses). La escasez de casos y la cercanía al cero provoca que todos los modelos concebidos para ofrecer un valor estimado y un intervalo de confianza alrededor de éste, traigan como consecuencia la aparición frecuente de límites de confianza inferiores negativos, lo cual en nuestro marco resulta un desatino. Estas dificultades complican la búsqueda del método adecuado para poder predecir estas enfermedades y sin embargo, esta predicción resulta tanto o más necesaria que para el resto, por cuanto los eventos raros o poco frecuentes pueden convertirse o manifestarse como enfermedades ree-mergentes, las cuales con más razón deben ser vigiladas de cerca. Hasta ahora, hemos basado nuestro análisis en la observación de las diferencias entre las tasas de incidencia de cada provincia con relación a la tasa nacional, esto nos ha permitido apreciar la variación del riesgo a ese nivel comparado con el riesgo nacional. Para ello empleamos en los reportes habituales, tablas y figuras que ilustran estas diferencias entre las provincias y el país.
Sin embargo, con ninguno de éstos métodos se puede determinar con exactitud si en algún municipio del país se está produciendo un incremento alarmante en el número de casos y por ende un aumento en el riesgo de enfermar, pues por una parte la utilización de las tasas de incidencia en áreas geográficas pequeñas como pueden ser algunos municipios, resulta improcedente por cuanto en las poblaciones pequeñas estas tasas son inestables y no permiten evaluar con precisión la verdadera magnitud del riesgo. Por otro lado, la cantidad de municipios existentes en el país hace inoperante la confección de las figuras necesarias.
Es ante esta situación, donde resulta útil disponer de un método el cual, con un determinado grado de certeza, nos permita conocer cuánto se acerca o se aleja el comportamiento observado del esperado establecido con anterioridad, de manera que se pueda evaluar mejor la distribución del problema en los municipios. Para ello resulta bastante aceptable la utilización de la distribución de probabilidades Poisson, similar a como viene apareciendo desde hace algún tiempo en el reporte Warner del CDR weekly (Communicable Disease Report)10 del PHLS Communicable Disease Surveillance Centre de Inglaterra.
La distribución Poisson es ideal para predecir el número de sucesos (casos) que se producirán en un determinado período de tiempo, cuando se trata de eventos raros que se asume ocurren de manera aleatoria en el tiempo. La ventaja del empleo de esta distribución está dada porque permite obtener la probabilidad de ocurrencia, del evento según su comportamiento medio anterior, pues los parámetros de la misma son los siguientes:11-13
e-l l x
P (X = x) =
x
donde:
l : es el promedio de ocurrencia del evento (media aritmética de los casos en un período determinado).
x: es el número de veces que ocurrió el suceso (número de casos).
Como ejemplo de la utilización de esta distribución tenemos que, si deseáramos comparar el comportamiento de la leptospirosis durante la primera semana de 1999 con relación a su comportamiento medio anterior, podríamos utilizar la media semanal de casos de leptospirosis en el país durante el período 1990-1998 para la semana número 1 (4 casos) , mientras que en la semana 1 de 1999 se reportaron 9 casos, la probabilidad Poisson es P(X=9) =0,0132 para estos valores de los parámetros. Si tomamos como nivel de confianza a=0,05 para decidir sobre nuestra hipótesis de diferencias entre lo observado y lo esperado, entonces podemos plantear que en 1999 el número de casos observados en la primera semana es significativamente diferente de lo esperado.
No obstante, en nuestro caso como se trataba de evaluar el comportamiento de las enfermedades en los diferentes municipios del país decidimos considerar que la tasa de incidencia nacional constituye la referencia idónea para determinar los casos esperados en cada municipio. Por consiguiente, para realizar el análisis se obtiene el número esperado de notificaciones en cada municipio multiplicando la tasa nacional para el evento en cuestión por la población en riesgo de sufrir el evento en cada uno de los municipios. En las tablas 3 y 4 se muestran los resultados obtenidos al aplicar este método a la incidencia de hepatitis viral en algunos municipios de la Ciudad de la Habana, durante la semana número 15 del año 1999. En esa semana en el país se reportaron 315 casos y la tasa de incidencia nacional fue de 2,85 por 100 000.
Entonces, pueden compararse los casos observados y los esperados de la misma forma que cuando utilizamos el promedio, obteniendo las probabilidades correspondientes en la distribución Poisson y decidiendo acerca de la significación o no de las diferencias. Si se desea disminuir la probabilidad de error se pueden tomar valores de a tan pequeños como se quiera, por ejemplo 0,005, con lo cual se dificultará aún más el rechazo de nuestra hipótesis. Observe que los municipios que tuvieron un comportamiento significativo al del país fueron Playa, Plaza, Centro Habana y Regla (a £ 0,05); sin embargo esta diferencia se presentó lo mismo por exceso que por defecto y en realidad lo que nos interesa es remarcar cuando el número de casos observados excede al número de esperados.
Para determinar de una manera fácil y rápida cuáles son los municipios donde el reporte excede lo esperado según la tasa nacional y ayudar en la toma de decisiones al respecto, se construyó un indicador que no es más que la razón entre lo observado y lo esperado, el cual se calcula para todos los municipios que resulten significativamente diferentes de la tasa nacional. Este indicador refleja la magnitud de la diferencia, si este es < 1, significará que se ha producido un reporte superior a lo esperado cuya importancia será directamente proporcional al valor del mismo. En la tabla 5 se muestra el resultado final del análisis y podemos apreciar que de los cuatro municipios que habían presentado un comportamiento diferente al esperado, solamente en el caso de Regla este fue significativamente superior:
| Municipios | | | | | |
| Playa | | | | | |
| Plaza | | | | | |
| C. Habana | | | | | |
| H. Vieja | | | | | |
| Regla | | | | | |
Otra de las maneras en que se puede utilizar este método es para identificar los municipios que al finalizar un año presentaron una incidencia significativamente superior a la del país. El siguiente ejemplo se elaboró con los datos de casos anuales de neuropatía epidémica de todos los municipios del país durante 1998. La tasa de incidencia nacional del período fue de 3,3 / 100 000 habitantes Después de obtener los casos esperados según esta tasa se procedió a efectuar la comparación mediante la distribución de probabilidad Poisson y la razón entre observados y esperados. Los resultados se muestran en la tabla siguiente, donde podemos observar los municipios cuya incidencia estuvo muy por encima de lo que hubiera podido esperarse si su comportamiento hubiera sido similar al del país. En todos esos casos la probabilidad según la distribución Poisson fue inferior a 0,05 y como se aprecia los valores del indicador calculado fueron superiores a 1(tabla 6).
| | | | | |
| Mantua | | | | |
| P. del Río | | | | |
| S. J. y Martínez | | | | |
| Guane | | | | |
| N. Paz | | | | |
| 10 de Octubre | | | | |
| La Lisa | | | | |
| C. de Ávila | | | | |
| Camagüey | | | | |
| R. Cauto | | | | |
| Jiguaní | | | | |
| Bayamo | | | | |
| Stgo. De Cuba | | | | |
| Guantánamo | | | | |
| Baracoa | | | | |
Existen numerosos municipios donde la enfermedad se mantuvo durante el año dentro de los límites que pudiéramos considerar como normales. Para tener una mejor apreciación del comportamiento del evento en todo el país se confecciona una figura con los valores de la razón entre observados y esperados, aún cuando la diferencia entre ambos valores no haya sido significativa, en este gráfico se aprecia con facilidad donde están las principales dificultades en el país pues los municipios están codificados en orden sucesivo de occidente a oriente (excepto la Isla de la juventud que es el 169), con una observación rápida de la figura se observa que en los extremos del país se presenta mayor cantidad de municipios con tasas muy altas, así como de territorios con mas casos de los esperados, de acuerdo con la notificación nacional (fig. 2).
FIG.2 Neuropatía Epidémica. Comportamiento de la razón entre tasas observadas y esperadas por municipios, 1998.
Consideraciones finales
Como se ha podido apreciar ambos métodos son bastante sencillos y fáciles de aplicar para la vigilancia en cualquiera de los niveles del sistema. No obstante, el método que utiliza a la distribución Poisson está recomendado para los territorios pequeños en el análisis de muchas enfermedades y a escala nacional sólo para las enfermedades de baja frecuencia mientras que el método del comportamiento histórico puede ser utilizado indistintamente por todos los niveles siempre y cuando se disponga de buenas bases de datos y se cumplan los demás requisitos tratados en este artículo. De todos modos siempre recomendamos la utilización de varios métodos y sobre todo el análisis integral de la información que éstos brindan complementada con la opinión de expertos, pues debe tenerse presente las ventajas y limitaciones de cada técnica para cada enfermedad y situación particular las cuales no deben sustituir la información cualitativa que estos aportan.
Por otra parte es necesario continuar trabajando en el perfeccionamiento de estas técnicas y adecuarlas a las condiciones reales del trabajo de cada instancia de nuestras unidades.
SUMMARY
One of the fundamental objectives of the work in the units of analysis and tendencies is to improve the surveillance methods used in the country so as to guarantee, the timely detection of any behaviour deviating from what is normally expected from health events of our concern. During the 5 years of operation of our units we have used different methods to achieve this purpose, taking into account the advances in this field abroad. We have recently started to use 2 new methods. The first of them is devoted to the comparison of what has been observed with the historical behaviour through a simple calculation procedure, while the second one is conceived for the processing of very low incidence events, which are difficult to treat with any of the traditional procedures, it uses Poisson distribution curve. Good results have been obtained with both methods since they allow the detection of deviations from the usual behaviour with enough accuracy and their use was recommeded in our provincial and municipal units. Subject headings: POPULATION SURVEILLANCE; INVESTIGATIVE TECHNIQUES.
REFERENCIAS BIBLIOGRÁFICAS
- Thacker, S; Berkelman, R. Public Health Surveillance in the United States. Epidemiologic Reviews. Vol 10;1988:168-70.
- Thacker, S; Berkelman R: Stroup. D. The Science of Public Health Surveillance. Journal of Public Health Policy Summer; 1990:187-88.
- Thacker, SM Commentary. Symposium of statistics in Surveillance. Statistics in Medicine. 1989; Vol(8):363.
- Berkelman,R. Summary Remarks. Symposium of Statistics in Surveillance. Statistics in Medicine 1989;Vol(8)393-5.
- Aguirre J. Introducción al tratamiento de Series temporales. Aplicaciones a las Ciencias de la Salud. Medrid. Díaz de Santos; 1994:90-115.
- Wei W. Univariate and multivariate Time Series Analysis. New York: Mc Graw Hill;1994:223-75.
- Stroup. D, Williamson. G, Herndon. J, Karon J. Detection of aberrations in the Ocurrence of Notifiable Diseases Surveillance Data. Stat in Med;1989:8(3):323-9.
- Stroup. D, Wharton. M, Kafadar. K, Dean.A. Evaluation of a Method for Detecting Aberrations in Public Health Surveillance Data. Am J Epidem, 1993.137(3):373-81.
- Wharton, M. Price, W.Hoesly, F et al. Evaluation of a Method for detecting Outbreaks of Diseases in Six States. Am. J. Prev. Med. 1993;9(1):45-8.
- Weekly Analysis Report of Notifications. Commun Dis Rep CDR Wkly 1998;8:40-1.
- Freixa M. Anális exploratorio de datos. Nuevas técnicas estadísticas. Barcelona: Publicaciones Universitarias; 1992:266-7.
- Armitage P. Stastical Methods in medical research. London. Blackweel Publications;1997:326-40.
- Steel T. Principles and procedures of Statistics: A Biometrical Approach. New York, Mc Graw Hill. 1994:528--30.
Recibido: 28 de julio de 1999. Aprobado: 19 de enero del 2000.
Dra. Gisele Coutin Marie. Avenida del Bosque No. 58, Nuevo Vedado, Plaza de la Revolución, Ciudad de La Habana, Cuba.
1 Especialista de I Grado en Bioestadística y en Administración de Salud.
2 Licenciado en Matemáticas.
3 Especialista de primer Grado en Medicina General Integral y Máster en Epidemiología
4 Especialista de I Grado en Epidemiología.
Especialista de I Grado en Medicina General Integral y Máster en Atención Primaria.