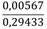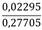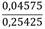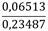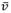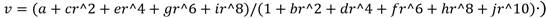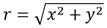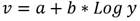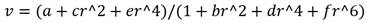Introducción
La capacidad de predecir con precisión los parámetros del flujo aguas arriba y aguas abajo de un accesorio colocado en serie, es crucial para garantizar un diseño eficiente y seguro de los sistemas de tuberías.
Toda investigación encaminada a solucionar problemas asociados a accesorios en tuberías a presión tiene relevancia tanto en el ámbito académico, como en el industrial, ya que su impacto contribuirá al avance del conocimiento y a la mejora de las prácticas de diseño y operación de sistemas de tuberías. Esto permitiría a los ingenieros y diseñadores tomar decisiones acertadas sobre el rendimiento y eficiencia de los sistemas de tuberías, así como validar los resultados obtenidos con las normas y estándares establecidos.
La utilización de herramientas de simulación numérica, como la Dinámica de fluidos computacional (CFD), permite evaluar diferentes configuraciones de geometrías, mallado, parámetros del flujo y modelos de turbulencia que permiten un análisis computacional de la solución y una vez calibrado el modelo, permiten hacer un estudio exhaustivo de las mejores alternativas de su implementación y cuantificar los efectos sobre el flujo que el accesorio provocará (Stefano et al., 2021).
Por otra parte, existe poca información publicada que profundice en los criterios que deben seguirse, en el caso de flujos computacionales, al definir las longitudes de tubería, en la cual irá insertada una obstrucción artificial, tal como: una válvula, un flujómetro del tipo deprimógeno, un estabilizador de flujo, etcétera. La simulación numérica CFD es una herramienta capaz de ofrecer esta información con relativamente poca inversión y tiempo. Al emprender este tipo de simulaciones el especialista se enfrenta a numerosas variables a valorar hasta lograr obtener los resultados deseados con mínimos errores que posibiliten hacer un uso adecuado de la información obtenida y poder llegar a conclusiones totalmente válidas.
Si a lo anterior se le suma, que los modelos CFD requieren de un potencial de cómputo nada despreciable, si se quiere llegar a respuestas ingenierilmente aceptables, entonces, se deben decidir, con mucha precisión, la cuantificación de un número de variables que influyen en la respuesta que dará el modelo y en el tamaño de almacenamiento que el mismo tenga y que influye decisivamente en las capacidades de la computadora a emplear y en el tiempo de cómputo de cada corrida.
El trabajo que aquí se expone se centrará en algunas de esas variables como son: la decisión de la longitud de los tramos de tubería a estudiar, la densidad del mallado y el criterio de parada empleado para aceptar la solución.
Antecedentes sobre soluciones CFD
La Dinámica de fluidos computacional (CFD) surge entre las décadas de los años 50 y 60 del pasado siglo, de manos de John D. Anderson en 1995, citado por Chirino (2023). CFD es una de las ramas de la Mecánica de fluidos que utiliza métodos numéricos y algoritmos para resolver y analizar problemas sobre el flujo de fluidos.
A grandes rasgos el método en discretizar una región del espacio, creando lo que se conoce por una malla espacial, dividiendo esa región en pequeños volúmenes de control. Después se resuelve, en cada uno de ellos, las ecuaciones de conservación discretizadas, de forma que, en realidad se resuelve una matriz algebraica en cada celda de forma iterativa. El proceso de cálculo se prolonga hasta que se alcance el valor del residuo de las variables que intervienen en el proceso, declarado en la construcción del modelo, o, hasta que visualmente el especialista verifique, después de un grupo de iteraciones, que los residuos se mantienen constantes.
En gráficos por computadora, los primeros intentos para resolver las ecuaciones de Navier-Stokes en 3D lo hicieron Foster y Metaxas en 1996, del Center for Human Modeling and Simulation. Ellos basaron su trabajo, en un artículo clásico de CFD del año 1965 publicado por Harlow y Welch en 1965, (Chirino, 2023).
En el campo del CFD uno de los paquetes más utilizados los proporciona la empresa ANSYS Inc. en su paquete computacional propietario ANSYS y una versión limitada para estudiantes (ANSYS Academic Student). Pero, no son los únicos y en código abierto, al acceso de todos, está cobrando mucha fuerza el OpenFOAM (Open Field Operation and Manipulation).
Desde esa época y hasta hoy se han presentado en revistas, congresos y libros, numerosos trabajos sobre el uso de CFD para la solución de problemas de la ciencia y la ingeniería.
En los últimos años han sido publicados numerosos trabajos relacionados con fluidos. Villaroel (2015), en su tesis de maestría, al evaluar una válvula de mariposa emplea para la longitud aguas arriba una distancia de 6 diámetros y 15 diámetros para la longitud de tubería aguas abajo, sin entrar en detalle de como validaron esas longitudes. Por su parte, Lluguay en 2016, citado por Chirino (2023), desarrolla un modelo CFD para el análisis del comportamiento del fluido en tuberías sin abordar el tema de las longitudes idóneas para una simulación. Chirino (2023), en su tesis de grado cita también a Ordoñez et al. (2018), que publica un estudio, donde el objetivo principal es desarrollar un modelo CFD para el análisis y simulación de los perfiles de velocidad en el banco de pérdidas del laboratorio de turbomáquinas hidráulicas.
Recientemente, Barros y un grupo de colaboradores en el año 2022, citado por Chirino (2023), llevaron a cabo un estudio en la Universidad de Estadual de Campinas en Brasil donde desarrollaron y validaron un procedimiento diseñado para utilizar la dinámica de fluidos computacional (CFD) para estimar con precisión la caída de presión del flujo de agua a través de placas perforadas con orificios delgados biselados, sin que en el mismo se detalle el cálculo de las longitudes de tubería empleadas.
También en el año 2022, Khayat y Afarideh, citado por Chirino (2023), plantean que las simulaciones con herramientas de la dinámica de fluidos computacional es un método numérico válido para predecir el flujo de dos fases en flujómetros Venturi, pero no abunda en el diseño del modelo necesario para llevar a cabo el estudio.
Importante es resaltar que, en 2008, el National Institute of Standards and Technology de Estados Unidos de América, utilizó ANSYS, para modelar las causas y efectos del desplome del edificio World Trade Center, durante el atentado del 11 de septiembre de 2001, citado por Chirino (2023).
En su trabajo de tesis de grado Chirino (2023) recopila, en breve síntesis, los trabajos desarrollados en el Centro de Investigaciones Hidráulicas (CIH) del Instituto Superior Politécnico “José Antonio Echeverría”, hoy Universidad Tecnológica de La Habana “José Antonio Echeverría”.
En la citada institución cubana, se han presentado trabajos basados en el empleo de herramientas CFD, desde hace más de dos décadas y se han impartido por el profesor Doctor Alejandro P. Prieto, cursos optativos a los estudiantes de Ingeniería Hidráulica. Dentro de los estudios realizados en el CIH, se encuentran: la investigación dirigida por A. J. León realizadas por Márquez (2002), que aborda un estudio sobre la modelación, en conducciones forzadas, con el empleo de ANSYS; y para darle continuidad a ese estudio la tesis de grado de Vélez (2003). Posteriormente en el año 2012, se publica un trabajo sobre conducciones libres utilizando, otra herramienta computacional CFD, el programa FLOW 3D (León y Herrera, 2012).
Otra de las tesis con la que cuenta el CIH, que aparece citada por Chirino (2023), es la de maestría desarrollada por Bosch (2015), dirigida por A. J. León y A. Prieto, sobre el comportamiento de las obras hidráulicas, siendo la primera tesis de maestría en Ingeniería Hidráulica defendida en Cuba sobre la aplicación de modelos CFD a estas obras.
Otro de los trabajos es la tesis de grado defendidas en el año 2017 por Izquierdo (2017), dirigidas por A. J. León, donde se desarrolló un trabajo metodológico sobre la construcción de modelos de conducciones forzadas con herramientas CFD.
Más reciente, se encuentra el trabajo de Stefano et al. (2019), con recomendaciones básicas para modelar obras hidráulicas en canales, empleando CFD. Por su parte, Asen (2019), presenta su tesis de diploma dirigida por A. Prieto y J. Ramírez, dedicada a la simulación de la ruptura súbita en tuberías de agua, empleando ANSYS CFX y ANSYS Fluent.
También se aborda, más recientemente, el tema de la modelación de tuberías con CFD en una publicación dedicada a los flujómetros proporcionales (León et al. 2022).
De los trabajos publicados en Cuba, ninguno aborda el tema de la longitud ideal de los tramos de tubería, pero sin embargo en varios de ellos (Márquez, 2002; Vélez, 2003; León y Herrera, 2012; Izquierdo, 2017; León, Ramírez y Stefano, 2022) se aborda el tema de la simulación del comportamiento de accesorios en una tubería.
Es de resaltar que, en muy pocos de los trabajos internacionales consultados, se aborda el tema de la longitud de los tramos de tubería a emplear, en consonancia con el mejor rendimiento del modelo y la obtención de resultados válidos y con bajos errores. El resto de la búsqueda de trabajos publicados en otros países y que aparecen en Chirino (2023) y que, por limitaciones propias de esta revista no pueden ser incluidos, no arrojó ningún resultado destacable.
Por la razón anterior, el grupo de recomendaciones que se presentarán a continuación se espera que contribuyan en el futuro a un mejor empleo de esta importante y útil herramienta computacional en la búsqueda de mejores soluciones.
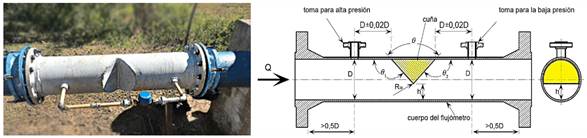
Para el desarrollo que a continuación se expone se empleará como accesorio insertado en serie en la tubería el flujómetro de Cuña (Wedge Meter) validado recientemente por la SASO ISO 5167-6 (2020) y para su modelación, se empleará la componente CFX del ANSYS.
ANSYS CFX es una herramienta CFD de propósito general, muy potente para el análisis ingenieril y el diseño de problemas relacionados con flujos de fluidos, transferencia de calor, reacciones químicas, problemas de combustión, etc. CFX es un solucionador basado en la presión (pressure based solver) que no necesita una corrección especial para Números de Mach bajos.
El objetivo del presente trabajo, es transmitir la experiencia de los autores, trabajando con ANSYS CFX, acerca del diseño inicial de tuberías que contienen accesorios, con el objetivo de minimizar el número de elementos del mallado y así disminuir el espacio de almacenamiento del modelo y el tiempo de cómputo necesario para su solución.
Consideración sobre las longitudes de tubería aguas arriba y aguas abajo de un accesorio.
Las longitudes de tubería aguas arriba y aguas abajo de un accesorio, para una misma densidad de mallado, influyen de forma directamente proporcional en el número de nodos y elementos de la malla de elementos finitos en que se subdivide el volumen del cuerpo a modelar; por tanto, tiene una relación directa con el costo computacional y el tiempo de ejecución de cada corrida. Por esta razón, la decisión que se tome influirá directamente, también, en la selección de la potencia informática de la PC a emplear, si se quiere llegar a una solución con bajos errores.
Longitud necesaria para la estabilidad del flujo aguas arriba (aarr) del accesorio
Las pruebas para determinar esta distancia tendrán como base los patrones de velocidad formados a lo largo del conducto, observando su estabilidad y reduciendo los tramos de la tubería donde ya se mantiene estable.
Entre las opciones de ANSYS CFX para ingresar el flujo en el conducto, se encuentra la de introducir un valor de velocidad. Esta última opción, tiene dos modalidades, introducir un patrón de velocidades homogéneo, o constante; o introducir un patrón de velocidades no homogéneo, o variable.
Para el trabajo se modeló una tubería de 300 mm de diámetro interior, 50 metros de largo y una rugosidad de 0,15 mm. Para la malla global y la malla local se empleó una inflación con 15 capas y en total para los 50 metros de tubería la malla se subdividió en 2,54E+06 nodos y 6,15E+06 elementos, o lo que es igual 5,00E+04 nodos y 1,20E+05 elementos por metro lineal de tubo.
Empleando la opción de introducir la velocidad como variable de entrada del flujo con la velocidad media que se quiere modelar formando un patrón homogéneo, se estudiaron en secciones desde la entrada del flujo hasta la salida de este en una tubería de 300 mm de diámetro interior, 50 metros de largo y una rugosidad de 0,15 mm.
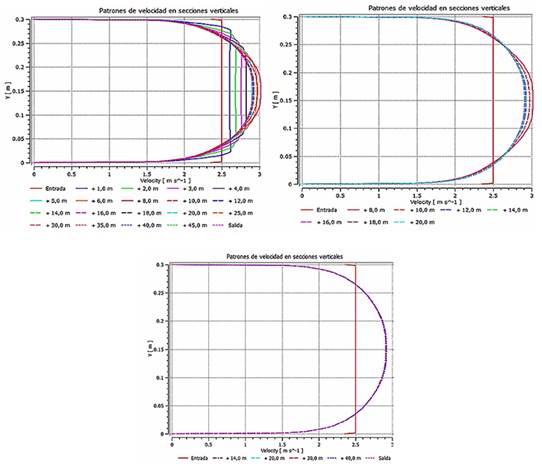
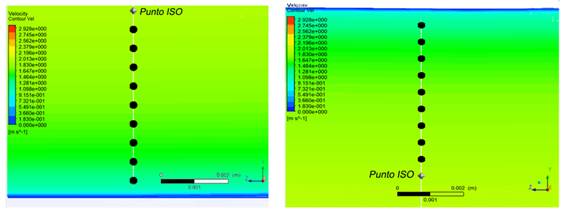
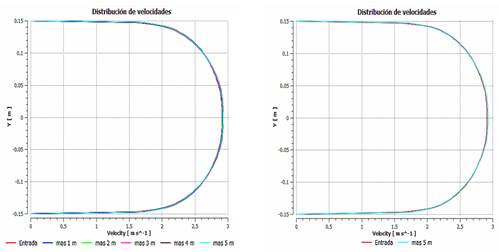
Se empleó para la evaluación de la longitud, la mayor velocidad a modelar, que para este caso fue de 2,5 m/s (ver figura 1).
Para el trabajo se empleó una PC con una placa base B365M DS3H, memoria GPU compartida 3,9 Gb, procesador Core I5 de 9na generación, 6 núcleos y 8 Gb de memoria RAM de 2666 MHz.
Se empleó, como criterio de parada que el RMS (Root Mean Square) que los residuos fueran menores que una millonésima (1E-06), mientras que el tiempo de ejecución fue de 1 hora 37 minutos para la entrada con patrón homogéneo de 2,5 m/s y alrededor de 1 hora 7 minutos para la entrada con el patrón no homogéneo que más adelante se empleará.
La figura 1, muestra las distribuciones de velocidades en diferentes secciones desde la entrada, donde se evidencia una estabilidad a partir de los 14 metros de la entrada (≈ 47D) el patrón de velocidades se mantiene estable, por lo que, si el accesorio hubiera estado ubicado en el medio del tubo (aproximadamente 25 metros aguas abajo de la entrada y 25 metros aguas arriba de la salida), podía prescindirse de 10 metros de tubería aguas arriba del accesorio, con lo cual se reduce en 5,00E+05 nodos y 1,22E+06 elementos, con el consiguiente ahorro de costo computacional y tiempo de cómputo.
Al patrón estable se le mide la velocidad media que representa, empleando para esto los normado por el método avalado por la BS ISO 3966 (2008), que establece la posición de los puntos de medición en una tubería con un tubo de Pitot para la determinación del caudal por el método aritmético, figura 2.
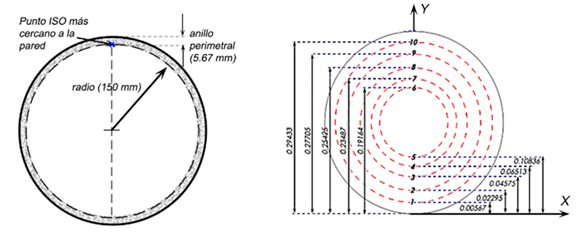
Figura 2 Sección de la tubería donde se resaltan los puntos para medir la velocidad media por la BS ISO 3966 (2008) y el anillo más cercano al perímetro interno de ducto.
Del procesamiento de la información que se obtiene del patrón estable de velocidades a 14,0 metros de la entrada del flujo, según el método Log-Lineal de la BS ISO 3966 (2008); es el resultado que aparece en la tabla 1. Este resultado indica el bajo error relativo (-0,245%) de la velocidad media real del patrón, estable y no homogéneo, que se forma a los 14,0 metros de la entrada; respecto a la velocidad media que se quiere emplear para la simulación de accesorio.
Tabla 1 Resultado de la medición de la velocidad (v) media del patrón estable de velocidad
*la coordenada Y= 0,00 metros, está en la invertida de la tubería
Reducción de la longitud aguas arriba (aarr) del accesorio aplicando un perfil de velocidad en la entrada
La segunda variante empleada para acortar el tramo aguas arriba, de un supuesto accesorio colocado en la sección media de la tubería (25,0 metros aguas abajo de la entrada y 25,0 metros aguas arriba de la salida), fue la de llevar a una ecuación, el patrón estable de velocidades que CFX creó en la prueba anterior, en una tubería de igual diámetro, igual rugosidad (material del tubo), igual mallado e igual modo de turbulencia que el que se empleará para evaluar el accesorio.
Para garantizar la simetría del patrón y dado que las diferencias entre las velocidades, para los puntos simétricos (1 y 10; 2 y 9; ...) difieren en menos de 0,078%, se calcula una distribución simétrica de velocidades, promediando la mismas a ambos lados del centro. En la tabla 2, aparecen las velocidades del patrón de velocidades simétrico. En cada celda donde aparecen las coordenadas de los dos puntos simétricos, que caracterizan el patrón, los números en la parte superior de la línea horizontal son las distancias, dadas por la ISO3966 (2008), entre el cetro del conducto y su invertida, medidos a partir del centro.
A partir de los datos obtenidos del patrón de velocidades, de acuerdo con la máxima cantidad de puntos recomendados por la BS ISO 3966 (2008) y agregándole a estos puntos, la velocidad en el centro de la tubería, medida con la herramienta probe del módulo de posprocesamiento del ANSYS CFX, se obtiene la expresión matemática (1), que modela, con un error estándar (Standard Error) de 2,76E-16 y un coeficiente de determinación (r2) de 1,0; el patrón de velocidades que debe imponerse, a la entrada del conducto. Debe resaltarse que este patrón ajustado no tiene en cuenta la distribución de velocidades que se produce en el anillo perimetral; que va desde la circunferencia que contiene los puntos 1 y 10, hasta la pared (ver figura 2).
Donde:
a, ..., j |
constantes de la ecuación y su valor es función de la velocidad media con la cual se evaluó el patrón. Para el caso de estudio, los valores aparecen tabulados en la tabla 3. |
r |
distancia, medida sobre un radio, que separa el punto de velocidad v del centro de la sección del ducto. Esta distancia se evalúa de acuerdo con la expresión (2). |
Tabla 3 Valores de las constantes del patrón estable de velocidades
| a= | 2,91578 | f= | -212141,3573979267 |
| b= | 51,15327262021717 | g= | 207171,4934702348 |
| c= | 140,1114577458863 | h= | 8721813,743396307 |
| d= | 4035,619288220024 | i= | -41271272,71169078 |
| e= | 4245,481875297239 | j= | -665017518,6421526 |
El patrón definido por la ecuación (1) y las constantes que aparecen en la tabla 3, se genera con los puntos definidos por la BS ISO 3966 (2008) más el punto central, considerando lineal la distribución de velocidades en el anillo perimetral. La cantidad de cifras de cada constante es importante mantenerlas para no alterar las velocidades que conforman el patrón.
Para imponer el patrón ajustado por la ecuación (1), se asume que la distribución de velocidades es lineal, a partir de los dos puntos BS ISO 3966 (2008) más cercanos al perímetro interno de la tubería y el propio perímetro interno (anillo de 5,67 mm para este diámetro).
Para el diseño geométrico que se evalúa, su mallado y las restricciones adoptadas en el Setup y con el fin de comprobar el error que se comete en con la suposición anterior, se distribuyeron 9 puntos en cada una de las dos zonas del anillo y se midió el valor de las velocidades, con la herramienta probe del módulo de posprocesamiento del ANSYS CFX.
En la figura 3 aparecen, de izquierda a derecha, los 9 puntos ubicados en la zona superior (anillo de 5,67 mm para este diámetro) y los 9 puntos ubicados en la zona inferior (anillo de 5,67 mm para este diámetro) y las distribuciones de velocidad para cada grupo y el patrón promedio para esa franja perimetral.
Según el método Log-Lineal que aparece en la BS ISO 3966 (2008) el patrón de velocidades cerca de la pared responde a la ecuación (3).
Evaluando los 9 puntos de la parte inferior y superior del anillo, promediando las velocidades en los puntos simétricos e incorporando, la velocidad media del punto más cercano, normado por la BS ISO 3966 (2008), (puntos 1 y 10, tabla 2), se obtienen los resultados que se muestran en la tabla 4 a partir de ajustar con la ecuación logarítmica, dada por el método Log-Lineal propuesto por la BS ISO 3966 (2008), para el anillo más cercano a las paredes del ducto, resultando un coeficiente de determinación r2= 0,9996951 y un Standard Error= 0,0038305
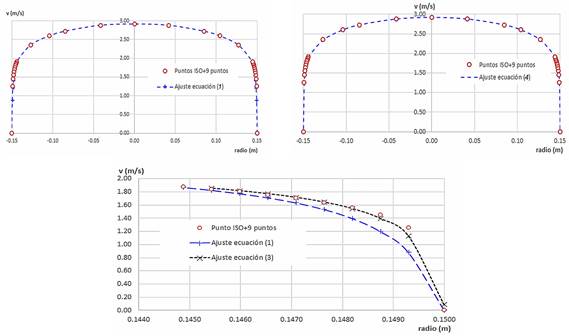
Para verificar la validez de suponer una distribución lineal, en el anillo más cercano al perímetro interno del ducto, se realizaron dos pruebas. Primero, se comparó el patrón de velocidades medido (los 10 puntos de la BS ISO 3966 (2008), más el valor del punto central más la suposición de que en el último anillo el patrón es lineal terminando en cero en la pared) con los resultados del ajuste realizado con el modelo matemático que aparece en (1), midiéndose los errores entre ambos, dando como resultado que varían en un intervalo entre +6,78E-13 % a -1,54E-14%, los valores indican, una vez más, que la expresión (1) ajusta los puntos medidos. En la figura 4, izquierda, aparecen los dos patrones: medidos y ajustados.
La segunda prueba incorpora los puntos medidos, con los de la velocidad de los nueve puntos que cuantifican la distribución de velocidades en el anillo perimetral, ajustando una nueva ecuación a la nube de puntos. La nueva expresión aparece en la expresión (4).
La expresión (4) es más simple que la (1) al tener menos términos formando el numerador y el denominador. El modelo matemático de ajuste, aunque con buenos resultados estadísticos, tiene mayores desviaciones que los que presenta el ajuste de la expresión (1). Las constantes (a, b, ..., f) que aparecen en la tabla 5 se generan con los puntos definidos por la BS ISO 3966 (2008), más el punto central, más la distribución de velocidades media medida en el anillo perimetral. Para este ajuste se obtuvo un coeficiente r2= 0,9961219 y un valor del Standard Error= 0,04763849.
Tabla 5 Valores de las constantes del patrón estable de velocidades
| a= | 2,92060107821163 | d= | 1012,462737166585 |
| b= | -67,90500046507253 | e= | 4054,116810927918 |
| c= | -221,0091877491234 | f= | 1639,567309474713 |
En la figura 4, izquierda, aparecen los patrones medidos y ajustados para la prueba con los puntos de la ecuación 1, correspondientes a la BS ISO 3966 (2008), más el punto central, considerando lineal la distribución en el anillo perimetral; en la propia figura, a la derecha, los patrones medidos y ajustados para la prueba que incorpora los nueve puntos del anillo perimetral (ecuación 4). Además, aparece al centro y abajo, una comparación, a mayor escala, de la diferencia entre los patrones ajustados, de las pruebas anteriores, cerca del perímetro interno del tubo.
Debido a la similitud entre ambos patrones, tanto medido como ajustado, decidió emplear el formulado por la ecuación (4) en la entrada de la tubería, por ser el que mejor representa la distribución de velocidades medidas con CFX, cercana a la pared.
Luego de obtener los resultados numéricos y gráficos se pasó a verificar, a partir de qué distancia de la entrada del ducto, se establecía un patrón estable de velocidades. Con este análisis se determina con mayor rigor la distancia de conducto aguas arriba del accesorio que debe emplearse.
La determinación de los patrones se realizó, muestreando 200 puntos de velocidad para cada patrón a partir de la entrada con intervalos regulares de 1,0 metro en dirección del flujo. En la figura 5, aparecen los valores de los patrones obtenidos. A la izquierda en la propia figura, todos los patrones con intervalos de 1,0 metro desde la entrada hasta la sección ubicada a 5,0 metros de la entrada y en la figura de la derecha, el patrón de entrada y el patrón a 5,0 metros de la entrada.
En la tabla 6 se muestra una valoración de las diferencias de las velocidades obtenidas entre cada patrón y el patrón de entrada empleando el error relativo medio. Se incluyeron los errores entre los patrones que se producen a 6 metros y a 7 metros de la entrada, para corroborar el resultado.
Visualmente no hay diferencias apreciables entre el patrón de entrada y los patrones cada un metro hasta cinco metros de la entrada, pero al analizar cuantitativamente las diferencias, se observan pequeñas variaciones que conducen a un mejor criterio acerca de la distancia que debe mantenerse aguas arriba del accesorio para que el patrón tenga estabilidad.
Tabla 6 Error máximo entre secciones transversales contiguas
| Intervalo | Entrada y 1,0 m | 1,0 m y 2,0 m | 2,0 m y 3,0 m | 3,0 m y 4,0 m | 4,0 m y 5,0 m | 5,0 m y 6,0 m | 6,0 m y 7,0 m |
| Error (%) | 1,27% | 0,63% | 0,88% | 0,59% | 0,28% | 0,30% | 0,29% |
El cálculo numérico de los errores que aparecen en la tabla 6, indican que a los 5,0 metros de la entrada se puede considerar estable el patrón de velocidades, y además la velocidad media del mismo tiene un bajo error cuantificado en -0,25%, con la velocidad que inicialmente se supuso para el ensayo.
En la tabla 7, se muestra una comparación entre la velocidad media a la entrada y en la sección ubicada a los 5,0 m de la entrada. Además, aparece el error de estas respecto a la velocidad media esperada de 2,5 m/s, donde se evidencia la factibilidad de emplear el perfil previamente generado con errores inferiores al 1%.
Tabla 7 Velocidad media según la BS ISO 3966 (2008) y error relativo respecto a 2,5 m/s
| Patrón de la entrada | Patrón a +5,0 metros | ||
| 2,489 m/s | -0,44% | 2,489 m/s | -0,43% |
Vale resaltar que es importante emplear la velocidad media calculada del patrón en el proceso de calibración del modelo en ANSYS, conteniendo el accesorio a investigar.
Determinación de la longitud necesaria y suficiente aguas abajo (aab) del accesorio a modelar.
El análisis para determinar la longitud aguas abajo del accesorio que se inserte, es un proceso semejante al anterior y reviste, también, mucha importancia, por lo que implica una menor longitud en el ahorro de costo computacional y tiempo de cómputo.
A diferencia del anterior análisis, en este caso es importante tener en cuenta el accesorio a modelar y su efecto sobre el flujo aguas abajo. De forma general si el accesorio tiene geometría constante (reducido, ampliaciones, etcétera), la determinación se realiza solo para la mayor velocidad de trabajo y este escenario dará el resultado esperado y con factor de seguridad para las velocidades menores.
Si el accesorio es necesario evaluarlo para diferentes estrechamientos, caso típico de flujómetros deprimógenos, válvulas, etc.; entonces la condición extrema debe cumplir ambas restricciones: máxima velocidad y mínimo estrechamiento.
Para los límites del presente trabajo, se analizó mediante simulaciones CFD el perfil de velocidad en un tramo de 25 metros aguas abajo de un flujómetro deprimógeno tipo Cuña (Wedge flowmeter), figura 6, observando y cuantificando aguas abajo del accesorio, la distancia a la cual el perfil comienza a tomar un patrón estable. Se empleó la máxima velocidad (2,5 m/s) y el menor valor de abertura para este flujómetro (h, figura 6) igual a 60 mm para un diámetro interior de conducto de 300 mm (h/D= 0,2; figura 6). Los resultados de los patrones de velocidad aguas abajo del flujómetro aparecen cuantificados en la tabla 8, donde se evidencia una estabilidad del perfil de velocidades a partir de los 10 metros con un error porcentual respecto a las secciones anterior y posterior de 0,148 % como máximo.
Tabla 8 Resultados del procesamiento de los patrones aguas abajo del vértice de la cuña.
| Secciones (m) | 4,0 a 6,0 | 6,0 a 8,0 | 8,0 a 10,0 | 10,0 a 12,0 | 12,0 a 15,0 | 15,0 a 20,0 |
| Error **(%) | 0,282 | 0,197 | 0,150 | 0,148 | 0,147 | 0,148 |
| v (m/s) | 2,486 | 2,491 | 2,489 | 2,489 | 2,490 | 2,488 |
*a partir del vértice de la cuña en dirección aguas abajo ** máximo calculado muestreando el patrón en 200 puntos
El patrón de velocidades estable en la tubería y su relación con el criterio de parada de las iteraciones en el cálculo
El ANYS tiene tres criterios de parada, el primero manualmente por el usuario al analizar las curvas del comportamiento de los errores (normalmente RMS o máximos) y de las variables del proceso. El segundo criterio viene dado por el número de iteraciones que el usuario elige al configurar el módulo Setup del CFX y el tercero por el límite del error impuesto, en el propio Setup, para las variables englobadas en masa (Mass) y momento (Momentum).
El criterio de parada influirá decisivamente en los resultados, así como las variables que se analicen. Cada problema en particular tiene sus propias características, pero en los límites del presente trabajo, el criterio de parada tiene influencia en el patrón estable de velocidades que se genera y por tanto tendrá influencia en la decisión de las longitudes de tubería a emplear, aguas arriba y aguas abajo.
Como ejemplo, se presentan en la tabla 9, resultados de los patrones generados aguas arriba del accesorio estudiado para criterios de parada para valores de 10-3, 10-4, 10-5 y 10-6.
Conclusiones
No se encontró en la literatura consultada sobre la simulación de tuberías a presión, todas perteneciente a los últimos 10 años, datos específicos en cuanto a cómo acortar los tramos de tubería con accesorio insertado, en un ensayo CFD.
En este estudio se demostró que, para un accesorio con una obstrucción muy fuerte y una velocidad relativamente alta, el empleo del patrón de velocidades que genera ANSYS CFX en una tubería de iguales características, muy larga y sin accesorio insertado, la dimensión del tramo aguas arriba, que garantiza un patrón estable para una modelación con rigor, equivalente a 16,7 veces el valor del diámetro interno del tubo (Laarr= 16,7D).
Para las mismas condiciones de obstrucción provocada por el accesorio y la velocidad del ensayo, la dimensión del tramo aguas abajo, que garantiza un patrón estable para una modelación con rigor, equivale a 33,3 veces el valor del diámetro interno del tubo (Laarr= 33,3D).
Por último, apoyando esta recomendación con los resultados de la tabla 8, se reafirma la necesidad de estudiar inicialmente, para cada accesorio en particular, el criterio de parada de cada corrida del modelo de simulación.