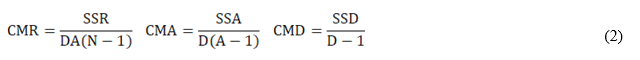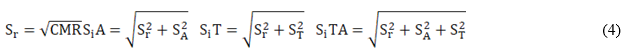Artículo original

Determination of Copper and Zinc by energy dispersive X-Ray fluorescence in modified natural Zeolites

Determinación de cobre y zinc por fluorescencia de rayos-X de dispersión de energías en zeolita natural modificada

0000-0003-2797-369XEvelin Valdés-Ríos^{1  *}  , 0000-0003-1568-4647Onibag Gutiérrez-Artiles²  , 0000-0002-3365-5885Juan Jiménez-Chacón¹  , 0000-0002-3322-0793Manuel Álvarez-Prieto² 

¹Institute of Materials Science and Technology, University of Havana, Havana. Cuba

²Faculty of Chemistry, University of Havana, Havana. Cuba

ABSTRACT

A procedure for the determination of Cu and Zn by Energy Dispersive X-Ray Fluorescence in naturals modified zeolites with these elements is presented. Reference samples of these materials were prepared and used for the procedure validation. The validation included the estimation of the following performance characteristics: scope, precision, bias and combined measurement uncertainty. The last tree characteristics were estimated at five levels of concentration defined by the reference samples. The precision was obtained in repeatability conditions and intermediate conditions, different analyst, different time and different time-analyst. The results obtained with the proposed procedure in the reference samples were compared with the results obtained in the same samples with the Flame Atomic Absorption Spectrometry. The comparison was carried out by linear regression using the iterative reweighted least squared method. No statistical significant differences were found between results.

Key words: modified zeolites; procedure validation; X-Ray fluorescence

RESUMEN

Se presenta un procedimiento para determinar el contenido de Cu y Zn por fluorescencia de rayos-X de dispersión de energías en zeolitas naturales modificadas con estos metales. Se prepararon materiales de referencia que fueron utilizados para validar el procedimiento. La validación contempló la estimación de los principales parámetros de desempeño del procedimiento: alcance, precisión, sesgo e incertidumbre combinada de la medición. Los tres últimos parámetros se estimaron a cinco niveles de concentración definidos por las muestras de referencia. La precisión se obtuvo en condiciones de repetibilidad y condiciones intermedias, diferente analista, diferente tiempo y diferente tiempo-analista. Los resultados obtenidos con el procedimiento propuesto en las muestras de referencia se comparan con los obtenidos para estas muestras por Espectrometría de Absorción Atómica. La comparación se llevó a cabo por regresión lineal, usando los mínimos cuadrados iterativamente reponderados. No se encontraron diferencias estadísticamente significativas entre los resultados.

Palabras-clave: zeolitas modificadas; validación de procedimientos; fluorescencia de rayos-X

Introduction

During the last 25 years, the Zeolite Engineering Laboratory of the Materials Science and Technology Institute of the University of Havana has focused its research on the design and development of new materials based on natural zeolites (NZ). These materials have been used to obtain high value-added products with applications in different branches of industry, especially those linked to the pharmaceutical sector. An example of this are the NZ modified with Cu or Zn that have microbicidal properties related to the oligo dynamic activity of the exchanged elements.

The NZ belonging to the Tasajera deposit meets the requirements established in the Cuban Standard 625 of 2008 ¹ for its use in the Cuban pharmaceutical industry. The analytical control of the exchanged element is of vital importance since it conditions the possible use of the material. To carry out this control, consolidated analytical techniques such as flame atomic absorption spectrometry (FAAS) and inductively coupled plasma optical emission spectrometry (ICP-OES) are used. Although with these techniques it is possible to obtain unbiased results with good precision, they require the dissolution of the sample prior to analysis, an extremely cumbersome process that involves a considerable consumption of time and chemical reagents.

Contrary to this, energy dispersive X-Ray fluorescence (EDXRF) is an analytical technique that has the advantage of presenting the sample to the instrument in solid phase, either in the form of loose powder or in briquettes of different sizes and thicknesses. In addition, it allows the determination of major and minor elements in diverse matrices in a precise and exact way. On the other hand, EDXRF is a non-destructive and environmentally friendly technique since it does not generate waste.

The objective of this work is to develop an analytical procedure by EDXRF in order to obtain reliable results of the Cu and Zn content in the modified NZ produced in the Zeolite Engineering Laboratory of the Materials Science and Technology Institute of the University of Havana. To achieve the above, it is necessary to validate the procedure and thus offer documented evidence that demonstrates that it is suitable to be used for that purpose.²

It is known that there are a large number of sources ^3-5 that provide general indications regarding how the validation of an analytical procedure should be carried out. However, there is no general consensus regarding the performance parameters of the procedure to be taken into account in the validation, so the diversity of terms and criteria prevails.⁶ However, those with the greatest incidence on the reliability of the result are the precision, the bias and the combined uncertainty of the measurement. The last performance characteristic is very important because of its great influence on the decisions that can be made with the result. For this reason, it is now required that all testing laboratories issue their results accompanied by the combined uncertainty of the measurement.⁷ Validation of an analytical procedure is not considered complete without estimation of this performance characteristic.

Materials and methods

Preparation of reference materials

The reference materials were prepared by weighing known amounts of NZ from the Tasajera deposit with CuSO₄5H₂O (ZN-Cu) orZnSO₄7H₂O (ZN-Zn) in a porcelain capsule. Subsequently, a small portion of deionized water was added and gently stirred with an agate pestle for 3 min. The mixture was dried at 100 ^oC in an oven and after cooling to room temperature it was homogenized for 5 min.

The contents of Cu and Zn expressed as a mass fraction in percent mass/mass in the reference materials were estimated according to:

where S is the weighed mass of CuSO₄5H₂O or ZnSO₄7H₂O,Zthe weighed mass of NZ and F is the ratio of atomic masses (gravimetric factor) of each element in its respective hydrated salt. The combined uncertainty (u_ref) associated with the C_ref concentration value was estimated as established in the Guide for the Expression of Uncertainty in Measurement (GUM).⁸

Samples reference preparation for FAAS measurement

The determinations were carried out on the samples selected for validation. About 0,1 g of each sample was weighed on graphite crucibles of 125 mL capacity. Then, 5 mL of 40 % HF were added, keeping the crucibles covered and at rest for 24 h. Once that time had elapsed, 1 mL of 60 % HClO₄ was added and heated on an electric hot plate until dense white fumes appeared. The contents of the crucibles were allowed to cool, 3 mL of 40 % HF was added, and heating was repeated until dense fumes. Subsequently, the walls of each crucible were washed with a fine stream of deionized water, 3 mL of 37 % HCl was added and heated until the sample dissolved. The crucibles were allowed to cooland the dissolved samples were transferred to a volumetric flask with a capacity of 100 mL. All reagents used were of analytical purity.

Instrumental conditions for FAAS spectrometer

Measurements were made in a Shimatzu model AA-6800 atomic absorption spectrometer operated under the instrumental conditions that appear in table 1.

Table 1 Instrumental conditions of measurement by FAAS 

Parameter	Cu	Zn
Wavelength (nm)	324,8	213,9
Band pass (nm)	0,2	0,2
Air flow (L/min)	10	10
C2H2flow (L/min)	1,8	2
Burner height (mm)	7	7
Burner length (cm)	10	10
Lamp current (mA)	6	8
Integration time (s)	3,0	3,0
Background correction	No	No

Preparation of tablets for measurement by EDXRF

0,5 g of H₃BO₃ and 1 g of modified zeolite sample were weighed out separately. The solids were transferred in that order to a stainless steel die in individual layers as homogeneously as possible. Finally, the die was placed in a hydraulic press and a pressure of 15 MPa was applied.

Instrumental conditions for EDXRF spectrometer

EDXRF measurements were performed on an Oxford Instruments energy dispersive X-Ray spectrometer model X-Supreme. This equipment consists of an SDD-type Si semiconductor detector with a resolution of 169 eV for Zn Kα and a 3-watt X-Ray tube with W anode. In addition, it has three types of primary radiation filters and offers the possibility of working in atmospheres of He and air.

Table 2 shows the measurement conditions under which all the spectra were recorded. The values ​​(keV) corresponding to the maximum of the analytical line Kα of the elements Cu and Zn and the lower and upper limits of the region of the spectrum around these maximums where the measurement of the area of ​​the signal in counts per second (cps) were carried out are also shown.

Table 2 Instrumental conditions of measurement by EDXRF. The values for Cu and 

Measurement condition		Value
Applied voltage to x ray tube (KV)		20
Applied current to the x ray tube (µA)		100
Radiation primary filter		W (5µm thickness)
Acquisition time of the spectrum (s)		120
Atmosphere		Air
Sample adaptor		Cd
Element	Maximum	Lower limit	Upper limit
Cu	8,04	7,85	8,24
Zn	8,63	8,50	8,80

Procedure validation

The validation of the analytical procedure included the estimation of the following performance characteristic: bias (Δ), scope, combined measurement uncertainty (u_c), precision in repeatability conditions (S_r), in intermediate conditions different analyst (SiA), different time (SiT) and different time-analyst (SiTA).

The precision, bias and uncertainty of the measurement were estimated at five concentration levels defined by the reference samples selected for validation. For this purpose, a validation experiment applied to each element was carried out.

The validation experiment is a fully nested three-factor design according to the ISO 5725-3⁹ standard. It was structured as follows: on D non-consecutive days (Factor 1) A analyst (Factor 2) made N determinations under repeatability conditions (Factor 3) of the Cu and Zn content by EDXRF in the corresponding reference sample.

Estimation of performance characteristics

Precision

The different precision estimates were obtained from the sums of squares and mean squares due to each factor in the nested design according to:

where:

SSR, SSA, and SSD are the sums of squares due to the repeatability, analyst and day factors, respectively.

CMR, CMA and CMD are the respective mean squares.

D, A and N are the number of days, the number of analysts and the number of replicates made by each analyst, respectively.

S_r ², S_A ² and S_T ² are the variances of repeatability, analysts and days, respectively.

Bias

The estimation of the bias and its associated uncertainty was carried out using two totally different procedures. The first is based on estimating the recovered:

and then the statistician t:

where C i is the average of the results obtained by the A analysts on each day, C_obs is the average of C i and constitutes the concentration value (%) estimated by EDXRF in the corresponding reference sample. The term δ is the bias in terms of recovery and u(δ) its associated uncertainty which was estimated according to Barwick and Ellison¹⁰, C_ref is the concentration of the reference sample and u_ref its uncertainty.

The value of the t-statistician obtained from equation (6) is compared with the critical values of the Student's t-distribution. If it is true that t_{1-α⁄2; D-1} ≤ t ≤ t_{1 - α⁄2; D-1}, the bias is not statistically significant for the selected confidence level α.

The second method is based on the comparison of the concentrations obtained by EDXRF in the reference samples (C_obs) with the corresponding concentration values obtained by FAAS (C_FAAS) according to:

The values of the intercept a and the slope b were estimated by linear regression using the Iteratively Reweighted Least Squares (IRLS) method¹¹. The bias evaluation was carried out from the joint estimation of the significance of the intercept and the slope by mean of its confidence ellipse.¹² The test result is best visualized as a plot of intercept vs. slope where the point (a, b) and the confidence ellipse are represented. If the point (a= 0, b= 1) is inside the ellipse, the bias of the EDXRF procedure is not statistically significant.

Combined measurement uncertainty

The combined measurement uncertainty was estimated according to:

where ∆= C_ref δ is the bias and u(Δ) is its associated uncertainty, both expressed in % mass/mass.

Scope

From four NZ samples belonging to deposits different from Tasajera, twelve reference materials were prepared (three for each sample) following the procedure described above. The differences in the content of SiO₂ in these samples with respect to that of the zeolite from the Tasajera deposit (60-68 %) was used as the main criterion for selection. The content of SiO₂ of such samples appears in table 3.

Table 3 SiO₂ content (%, mass/mass) of the NZ belonging to a deposit different from Tasajera 

	Z7	Z25	Z29	Z29	Z32
SiO2	51,10	46,38	54,78	54,78	68,62

Results and discussion

Table 4 shows the concentrations of Cu and Zn (C_ref) calculated using equation (1) for the reference materials prepared from the NZ belonging to the Tasajera deposit. The combined uncertainties (u_ref) associated with these concentration values ​​are included in the table. The first seven materials (P1 to P7) that appear for each element were used as calibration standards and the remaining ones (R1 to R5) as reference samples for the respective nested designs.

The tablets that were prepared according to the procedure described were resistant to handling, with well-defined faces and edges. This result rules out the use of binders, which implies weighing this and the reference material on an analytical balance and the exhaustive homogenization of the mixture of both. On the other hand, it would increase the time of the preparation being this more critical if it is necessary to analyze a large number of samples.

Table 4 Cu and Zn contents (C_ref) and associated combined uncertainties (u_ref) in the 

Cu			Zn
Name	Cref	uref	Name	Cref	uref
ZNCuP1	0,19	0,03	ZNZnP1	0,39	0,02
ZNCuP2	0,40	0,03	ZNZnP2	0,78	0,02
ZNCuP3	0,99	0,03	ZNZnP3	0,97	0,03
ZNCuP4	1,50	0,03	ZNZnP4	1,87	0,03
ZNCuP5	2,00	0,03	ZNZnP5	2,72	0,03
ZNCuP6	2,52	0,03	ZNZnP6	3,52	0,03
ZNCuP7	4,83	0,03	ZNZnP7	4,27	0,03
ZNCuR1	0,80	0,01	ZNZnR1	0,48	0,01
ZNCuR2	1,19	0,01	ZNZnR2	1,00	0,01
ZNCuR3	1,79	0,01	ZNZnR3	2,00	0,01
ZNCuR4	2,18	0,01	ZNZnR4	3,00	0,01
ZNCuR5	4,80	0,02	ZNZnR5	4,00	0,01

The selected measurement conditions (table 2) allowed the detector dead time in all measurements to be less than 20 % (manufacturer's recommendation). The use of the W filter considerably reduces the background and practically eliminates the W Lα line (8,39 KeV). This line belongs to the X-Ray tube and is scattered by the sample. If it appears in the spectrum, it constitutes a potential interference to the Kα of Zn (8,63 KeV). The spectrum acquisition time ensured that the relative standard deviation (RSD) of the analytical signal area was less than 1 %. The RSD was estimated according to:

where T is the acquisition time of the spectrum and A is the area under the analytical signal defined by the counts per second accumulated in the region of interest.

Estimation of the concentration in the validation samples

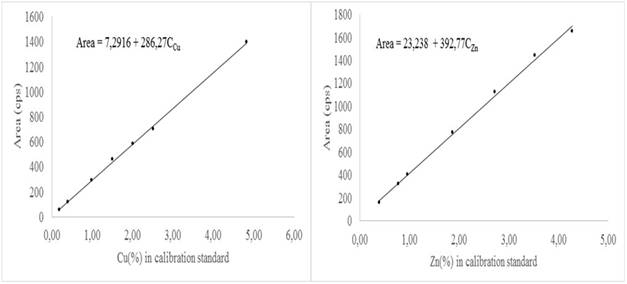
Figure 1 is the calibration curves for Cu and Zn in one of the days of execution of the nested design. As can be seen, the behavior of the area of ​​the analytical signal with respect to the concentration of Cu or Zn in the respective calibration standard is linear. This is an indication that the matrix does not exert any absorption or enhancement effect in the signal of both elements.

This behavior was observed for all the calibration curves obtained. Thus, the calibration function Area = I + PC was used to model this behavior. The values ​​of the intercept I and the slope P were estimated by ordinary least squares. This calibration function was used to calculate by analytical interpolation the content of Cu and Zn in the samples selected for validation.

Fig. 1 Behavior of the area of analytical line for Cu and Zn with respect to the concentration of element in the calibration standard. The equations inside the graph model the observed behavior 

Estimation of performance characteristics

Precision

Table 5 shows the results of the estimation of precision (%, mass/mass) in repeatability conditions (Sr), intermediate conditions different analyst (SiA), intermediate conditions different time (SiT) and intermediate conditions different time-analyst (SiTA). The analyst standard deviation (S_A) and the time standard deviation (S_T) also appear.

These values ​​were obtained by applying equations (2-4) to the results of the nested design where 3 analysts carried out on 4 non-consecutive days 2 determinations in repeatibity conditions of Cu and Zn content in the corresponding reference samples.

Table 5- Results of the precision estimates for the EDXRF procedure. All the results 

Zn
Cobs	Sr	SA	ST	SiA	SiT	SiTA
0,49	0,011	0,013	0,006	0,017	0,013	0,019
0,99	0,023	0,015	0,014	0,028	0,027	0,031
1,99	0,047	0,042	0,056	0,063	0,056	0,070
3,00	0,080	0,043	0,089	0,091	0,120	0,127
3,99	0,125	0,102	0,151	0,162	0,149	0,180
Cu
Cobs	Sr	SA	ST	SiA	SiT	SiTA
0,82	0,013	0,012	0,006	0,018	0,014	0,019
1,22	0,018	0,017	0,019	0,025	0,026	0,031
1,81	0,023	0,027	0,017	0,035	0,028	0,039
2,20	0,027	0,037	0,032	0,045	0,041	0,055
4,86	0,074	0,038	0,074	0,083	0,104	0,111

The ISO 5725-6¹³ standard establishes that in routine tasks the control of precision in repeatability conditions of the analytical procedure should be carried out by means of the maximum permissible deviation between replicates (MPD):

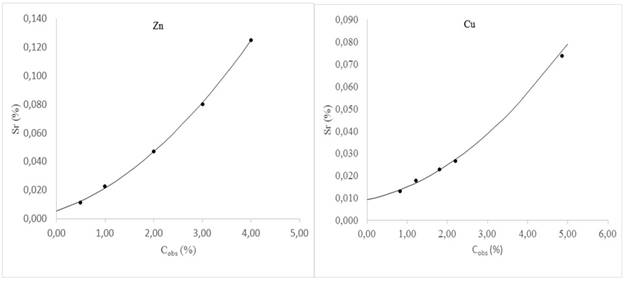
where T_0,95,n is a tabulated value that appears in the standard for different number of replicates n and 95 % confidence level. For n = 2, a value widely used in routine, the MPD = 2,8Sr. However, if the average of the replicates does not coincide with some concentration value of the validation samples, then it is necessary to use the so-called characteristic function¹⁴ to estimate the corresponding S_r and therefore the MPD.

Fig. 2 Behavior of S_r with respect to C_obs of Zn and Cu in the validation samples 

The characteristic function models the behavior of S_r with concentration and figure 2 is a graphical representation of that behavior. As can be seen, in both elements the increase in S_r with the increase in C_obs shows a non-linear trend. Thus, using the values of C_obs and S_r that appear in table 5, the respective characteristic function was obtained for Cu and Zn:

In routine tasks, the above equations allow the estimation of S_r for sample concentrations (obtained as an average of replicates) that do not coincide with the C_obs of the validation samples. In this way, it is possible to have the corresponding DMP and carry out the precision control as established by the aforementioned ISO 5725-6 standard.

Bias

The results obtained in the evaluation of the significance of the bias through the recovery are shown in table 6. In it, the tabulated values ​​for the recovery R, ​​the bias δ, its uncertainty u(δ) and the value of the statistician t were obtained from equations (5-8). As can be seen, for both elements the t-statistician is between the limits established by the critical values ​​of the Student's t-distribution for 95 % confidence and 3 degrees of freedom (D-1). Therefore, it can be stated with this level of confidence that there is no statistical evidence to affirm that the bias is significant, that is, it is accepted that there is no systematic error.

Table 6 Results of the bias evaluation through the recovery 

Zn
Cref	Cobs	R	δ	u(δ)	t	-t0,975,3	t0,975,3
0,49	0,49	1,00	0,004	0,04	0,08	-3,18	3,18
1,00	1,00	1,00	-0,003	0,02	-0,16
2,00	1,99	0,99	-0,007	0,01	-0,63
3,00	2,98	0,99	-0,007	0,02	-0,31
4,00	3,97	0,99	-0,008	0,01	-0,71
Cu
Cref	Cobs	R	δ	u(δ)	t	-t0,975,3	t0,975,3
0,82	0,82	1,00	0,005	0,03	0,15	-3,18	3,18
1,19	1,22	1,02	0,021	0,02	0,91
1,79	1,81	1,01	0,010	0,01	0,69
2,18	2,20	1,01	0,011	0,02	0,69
4,80	4,86	1,01	0,012	0,01	0,91

Although CuSO₄5H2O and ZnSO₄7H2O meet the requirement to be considered as reference materials of the composition, the possibility of changes in their structure during the preparation process of the reference materials according to the described procedure cannot be ruled out. This can influence the concentration values of the reference materials and therefore the results obtained with the EDXRFprocedure. For this reason, the estimation and evaluation of bias by regression was decided.

Table 7 shows the contents of Zn and Cu determined by FAAS in the reference samples selected for validation as well as the combined uncertainties associated with these concentration values ​​u(FAAS) estimated according to GUM⁸. These contents are the average of 3 replicates carried out by two analysts under repeatability conditions. The results obtained by EDXRF (C_obs) and its uncertainty S_r (values ​​taken from table 5) are also included.

Table 7 Results of the determinations by FAAS and EDXRF (C _obs) in the samples selected for validation. All the tabulated values are in % mass/mass 

Zn				Cu
Cobs	Sr	FAAS	u(FAAS)	Cobs	Sr	FAAS	u(FAAS)
0,49	0,011	0,44	0,02	0,82	0,013	0,89	0,02
1,00	0,023	0,94	0,03	1,22	0,018	1,17	0,01
1,99	0,047	2,06	0,04	1,81	0,023	1,84	0,03
2,98	0,080	2,95	0,06	2,20	0,027	2,33	0,03
3,97	0,125	4,02	0,08	4,86	0,074	4,98	0,03

Figure 3 is a graphic representation of the estimated concentrations of Zn and Cu in the reference samples by EDXFR (C_obs) and FAAS. The figure also shows the result of the linear regressions by IRLS.

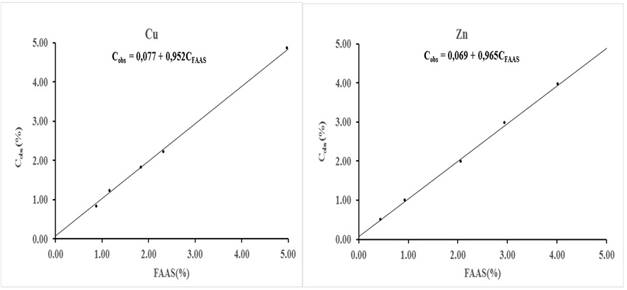
Fig. 3 Behavior of the results of Zn and Cu determination by FAAS in the reference samples with respect to the obtained in the same ones by EDXRF. The value of the intercept and slope of the equations in the graphic were estimated by IRLS regression 

The FAAS is an analytical technique with chemical-physical fundamentals completely different from those of the EDXRF. The way the sample is presented to the instrument is also totally different. Consequently, if the intercept and slope of the linear equations that appear in figure 3 are not statistically different from zero and one, respectively, it is possible to affirm that the bias of the EDXRF procedure is not significant in the validation interval. IRLS regression was used because it considers the uncertainties associated with the results of the two methods in estimating the intercept and slope.

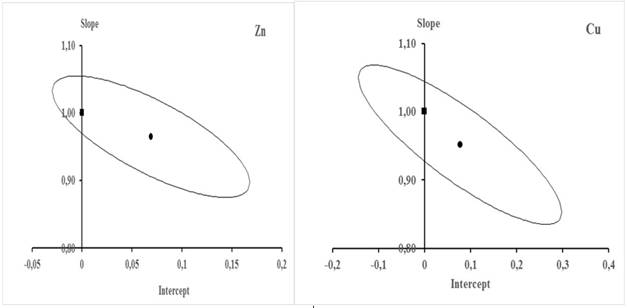
Fig. 4 Joint 95 % confidence interval (ellipse) of the intercept and slope (circle) belonging to the equations showed in figure 3. Thesquare represents the values intercept = 0 and slope =1 

Figure 4 shows the results of the joint significance test of the intercept and slope estimated by IRLS. The confidence level of the test was 95 %. As can be seen in the figure, the point (0,1); represented by a square, is within the ellipse that describes the joint 95 % confidence interval of the intercept and slope (circle). Therefore, it can be stated with this level of confidence that there is no statistical evidence to affirm that the bias of the procedure by EDXRF is significant. This test has the advantage that it includes the covariance between the intercept and the slope.

Estimation of bias using any type of linear regression allows its significance to be assessed globally over a concentration range. In addition, it is possible to know the type of bias if it is significant¹¹. However, it is not possible to estimate the bias (Δ_R) and its uncertainty u(Δ_R) individually for each of the concentrations in the interval. Borges and collaborators¹⁵ offer a way to estimate Δ_R and u(Δ_R) in this case:

Table 8 Results (% mass/mass) of the estimation of bias Δ_R and the associated uncertainty u(Δ_R) for the EDXRF procedure. The values of u(Δ) are showed for comparison purposes 

Cu
Cobs	FAAS	u(FAAS)	ΔR	u(ΔR)	u(Δ)
0,82	0,86	0,02	-0,04	0,053	0,024
1,22	1,15	0,01	0,07	0,060	0,028
1,81	1,82	0,03	-0,01	0,080	0,026
2,20	2,32	0,03	-0,12	0,096	0,036
4,86	4,98	0,03	-0,12	0,191	0,062
Zn
Cobs	FAAS	u(FAAS)	ΔR	u(ΔR)	u(Δ)
0,49	0,44	0,02	0,05	0,043	0,021
1,00	0,94	0,03	0,06	0,047	0,021
1,99	2,06	0,04	-0,07	0,061	0,023
2,98	2,95	0,06	0,03	0,076	0,071
3,97	4,02	0,08	-0,05	0,096	0,045

In table 8 it can be seen that for both elements u(Δ_R) is always numerically greater than u(Δ) and the difference between both tends to increase with the increase in C_obs. If equations (11) and (17) are compared, it is clear that four uncertainty components are involved in the estimation of u(Δ_R), while only two are involved in the estimation of u(Δ). In the case of u(Δ_R) the dominant components are those of the intercept, slope and covariance, however, for u(Δ) the contribution due to the reference material is practically negligible. In addition, u(Δ) is obtained from a nested experiment in which 24 replicates were made under repeatability conditions, while u(ΔR) is obtained from a regression with only five values.

Combined measurement uncertainty

Table 9 Results of the estimation of the combined measurement uncertainty for the determination of Cu and Zn by EDXRF. All the tabulated values in % (m/m) 

Zn
Cobs	SiTA	u(Δ)	u(Cobs)
0,49	0,018	0,021	0,03
0,99	0,031	0,021	0,04
1,99	0,070	0,023	0,07
3,00	0,127	0,071	0,15
3,99	0,180	0,045	0,19
Cu
Cobs	SiTA	u(Δ)	u(Cobs)
0,82	0,019	0,024	0,03
1,22	0,031	0,028	0,04
1,81	0,039	0,026	0,05
2,20	0,055	0,036	0,07
4,86	0,111	0,062	0,13

Table 9 reproduces the results of the estimation with equation (10) of the combined measurement uncertainty u(C_obs) associated to the C_obs concentration ​​obtained by EDXRF in the reference samples selected for validation. Values of the uncertainty of the estimation of the bias u(Δ) from the recovery are also shown.

In routine tasks is possible that an estimated concentration (C_est) of Cu or Zn does not coincide with some concentration of the validation interval (C_obs). In order to estimate the combined uncertainty of the measurement associated with C_est, it is necessary to obtain first the so-called uncertainty function¹⁶. This function describes the performance of an analytical procedure in terms of the behavior of the uncertainty in a concentration range. Furthermore, it is very useful when it is necessary to compare the value of C_est with a specification limit.¹⁷

From the data in table 9, the behavior of u(C_obs) with respect to C_obs was modeled for each element. Figure 5 is a graphical representation of that behavior.

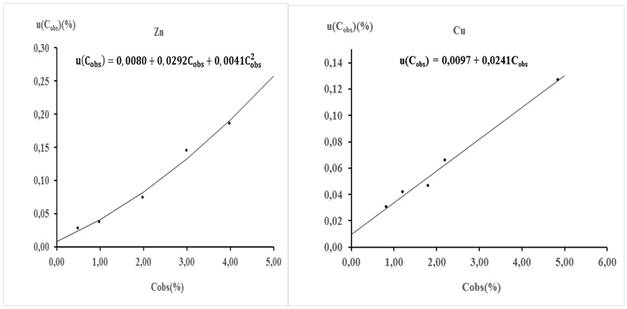
Fig. 5 Behavior of u(C_obs) with respect to C_obs in the validation interval. The equations showed in the figure are the respective characteristic functions 

In the case of Cu, it is observed that as C_obs increases the value of u(C_obs) increases linearly, while in Zn the increase of u(C_obs) with the increase of C_obs is parabolic. Figure 5 shows the respective functions that describe these behaviors and allow the estimation for each element of the combined uncertainty associated with any concentration value within the validation interval.

Scope

Table 10 shows the contents (C) of Cu and Zn estimated by EDXRF in the reference samples prepared with natural zeolites that not belong to Tasajera deposit. The corresponding combined uncertainty (u_c) and expanded uncertainty (U) values ​​are also shown, as well as the lower (LL) and upper (UL) limits of the coverage interval where 95 % of the values ​​attributable to the concentration C are found. The concentration values ​​of the reference samples (C_REF) were obtained from equation (1) and their uncertainties (u_REF) according to GUM⁸.

The concentrations of these samples are at the extremes and center of the concentration range of the reference samples used in the validation. The values of u_c in table 10 were obtained from the respective uncertainty functions that appear in figure 5. The expanded uncertainty was obtained as U = 2u_c while the limits of the 95 % coverage interval as LL =C - U and UL = C + U. The value of Z was estimated according to:

Table 10 Results of the Cu and Zn estimation in the reference samples prepared with natural zeolites that not belong to Tasajeradeposit 

Cu
Name	C	uc	U	LL	UL	CREF	uREF	Z
Z7CuR1	0,63	0,02	0,05	0,58	0,68	0,80	0,01	-6,1
Z7CuR2	1,46	0,04	0,09	1,37	1,55	1,80	0,01	-7,2
Z7CuR3	3,29	0,09	0,18	3,11	3,47	4,02	0,02	-8,1
Z25CuR1	0,67	0,03	0,05	0,62	0,72	0,80	0,01	-4,5
Z25CuR2	1,49	0,05	0,09	1,40	1,58	1,80	0,01	-6,5
Z25CuR3	3,31	0,09	0,18	3,13	3,49	4,01	0,02	-7,7
Z29CuR1	0,66	0,03	0,05	0,61	0,71	0,80	0,01	-4,8
Z29CuR2	1,55	0,05	0,09	1,46	1,64	1,81	0,01	-5,3
Z29CuR3	3,50	0,09	0,19	3,31	3,69	4,00	0,02	-5,2
Z32CuR1	0,74	0,03	0,06	0,68	0,80	0,80	0,01	-2,0
Z32CuR2	1,76	0,05	0,10	1,66	1,86	1,80	0,01	-0,7
Z32CuR3	4,04	0,11	0,21	3,83	4,25	4,00	0,02	0,4
Zn
Name	C	uc	U	LL	UL	CREF	uREF	Z
Z7ZnR1	0,44	0,02	0,04	0,40	0,48	0,51	0,01	-2,8
Z7ZnR2	1,70	0,07	0,14	1,56	1,84	1,99	0,01	-4,1
Z7ZnR3	3,28	0,15	0,30	2,98	3,58	4,00	0,01	-4,8
Z25ZnR1	0,44	0,02	0,04	0,40	0,48	0,51	0,01	-2,8
Z25ZnR2	1,76	0,07	0,14	1,62	1,90	2,00	0,01	-3,3
Z25ZnR3	3,64	0,17	0,34	3,30	3,98	4,00	0,01	-2,1
Z29ZnR1	0,47	0,02	0,05	0,42	0,52	0,51	0,01	-1,6
Z29ZnR2	1,85	0,08	0,15	1,70	2,00	1,99	0,01	-1,8
Z29ZnR3	3,69	0,17	0,34	3,35	4,03	4,00	0,01	-1,8
Z32ZnR1	0,51	0,02	0,05	0,46	0,56	0,51	0,01	0,0
Z32ZnR2	2,07	0,09	0,17	1,90	2,24	2,00	0,01	0,8
Z32ZnR3	3,96	0,19	0,38	3,58	4,34	4,00	0,01	-0,2

Values of Z ​​between -2 and 2 indicate that the C_REF is within the 95 % coverage interval of the values ​​attributable to C. For Cu, the above is only true in the reference samples prepared from Z32, although in one of them (Z32R1) the value of C_REF is equal to the upper limit UL. In the case of Zn, it is observed that Z is between -2 and 2 in samples Z32 and Z29, although in the latter C_REF is very close to the upper limit UL. The non-inclusion of C_REF in the interval C ± U is an indication of the presence of significant bias due to systematic errors caused by the different type of matrix between calibration standards and samples to be analyzed.

All of the above mentioned define the scope of the proposed procedure. This should be applied to determine Cu and Zn only in zeolites modified with these elements that belong to the Tasajeras deposit.

Conclusions

The inclusion of reference materials in the nested design allowed the precision, bias, and combined uncertainty of measurement to be estimated from the results of a single experiment. This is generally not possible to do because such materials are not always available in sufficient quantity and different concentration levels. The estimation and evaluation of the significance of the bias by regression allows us to affirm that CuSO₄5H₂O and ZnSO₄7H₂O do not undergo changes in their structure during the procedure for preparing the reference materials according to the procedure described. The instrumental conditions selected for the measurement of Cu and Zn in the X-Ray spectrometer made possible to obtain the area of ​​the analytical signal of these elements with a RSD less than 1 % and to keep this source of uncertainty at a low level. On the other hand, the use of the W filter makes unnecessary the use of background corrections by mean of mathematical processing of the spectrum. So, it was easy to obtain the area measuring directly the accumulated counts in the region of interest. The result of the validation of the procedure by EDXRF guarantees reliable estimates of the Cu and Zn during analytical control of the modified zeolites with these elements obtained in the IMRE Zeolite Engineering Laboratory.

References

1.  OFICINA NACIONAL DE NORMALIZACIÓN. Zeolitas Naturales-Requisitos. NC 625, 2008.

2.  HUBER, L. Validation and Qualification in Analytical Laboratories2.  . Second Edition. USA: Inform a Healthcare, 2007. ISBN 9780849382673.

3.  CURRIE-LLOYD, A. “Nomenclature in evaluation of analytical methods including detection and quantification capabilities”, Pure & Appl. Chem3.  . 1995, 67(10), 1699-1723. http://dx.doi.org/10.1351/pac199567101699.

4.  EURACHEM. The Fitness for Purpose of Analytical Methods. A Laboratory Guide to Method Validation and Related Topics4.  . First English Edition 1.0, 1998.ISBN 978-91-87461-59-0.

5.  THOMPSON, M.; ELLISON, S.; WOOD, R. “Harmonized guidelines for single-laboratory validation of methods of analysis”. Pure & Appl. Chem5.  .1995, 74(5), 835-855. DOI: 10.1351/pac200274050835.

6.  ÁLVAREZ, M.; JIMÉNEZ, J. “A fitness for purpose approach to validation and verification of analytical measurements”. Accred. Qual. Assur6.  . 2018, 23(4), 219-229. https://doi.org/10.1007/s00769-018-1331-y.0123456789.

7.  OFICINA NACIONAL DE NORMALIZACIÓN. Requisitos generales relativos a la competencia de los laboratorios de ensayo y calibración, NC ISO/IEC 17025, 2006.

8.  INTERNATIONAL STANDARD ORGANIZATION. Uncertainty of measurement - Part 3: Guide to the expression of uncertainty in measurement (GUM), ISO/IEC GUIDE 98-3:2008(E).

9.  INTERNATIONAL STANDARD ORGANIZATION. Accuracy (trueness and precision) of measurement methods and results - Part 3: Intermediate measures of precision of a standard measurement method, ISO 5725-3:1994(E).

10.  BARWICK, V. J.; ELLISON, L. R. “Measurement uncertainty: Approaches to the evaluation of uncertainties associated with recovery”, Analyst10.  . 1999, 124, 981-990. https://doi.org/10.1039/A901845J.

11.  RIPLEY, B. D.; THOMPSON, M. “Regression Techniques for the Detection of Analytical Bias”, Analyst11.  . 1987, 112, p. 377-383. https://doi.org/10.1039/AN9871200377.

12.  RIU, J.; RIUS, F. X. “Assessing the accuracy of analytical methods using linear regression with errors in both axes”, Analytical Chemistry12.  . 1996, 68(11), 1851-1857. https://doi.org/10.1021/ac951217s.

13.  INTERNATIONAL STANDARD ORGANIZATION. Accuracy (trueness and precision) of measurement methods and results - Part 6: Use in practice of accuracy values, ISO 5725-6:1994(E).

14.  THOMPSON, M. “The Characteristic Function, a Method-Specific Alternative to the Horwitz Function”, Journal of AOAC International14.  . 2012, 95 (6), 1803-1805. DOI:10.5740/jaoacint.12-042.

15.  BORGES-MIRANDA, A.; MARQUEZ-LEYVA, I.; PÉREZ-MARTÍNEZ; JIMÉNEZ-CHACÓN, J.; ÁLVAREZ-PRIETO, M. “Overcoming constraints of the control charting approach for measurement uncertainty assessments”, Accred. Qual. Assur15.  . 2015, 20 (6), 473-482. DOI 10.1007/s00769-015-1161-0. ISSN 0949-1775.

16.  THOMPSON, M. “Uncertainty functions, a compact way of summarizing or specifying the behaviour of analytical systems”, Trend in Analytical Chemistry16.  , 2011, 30 (7), 1168-1175. DOI:10.1016/j.trac.2011.03.012.

17.  ÁLVAREZ, M.; JIMÉNEZ, J. “Fitness for purpose in relation to specification limits”, Accreditation and Quality Assurance17.  , 2012, 17, 27-34. DOI 10.1007/s00769-011-0825-7.

Received: March 12, 2022; Accepted: June 01, 2022

^*Author for correspondence: correo electrónico: [e-mail]

The authors state that there are no conflicts of interest in the submitted manuscript.

Evelin Valdés Ríos: prepared Cu-modified zeolite reference materials. He participated as an analyst in the nested design, in the development of the FAAS procedure and carried out the Cu determinations in the reference materials. He worked on the writing of the article. Author for correspondence.

Onibag Gutiérrez Artiles: prepared Zn-modified zeolite reference materials. He participated as an analyst in the nested design, in which he developed the FAAS procedure and carried out the Zn determinations. He worked on the writing of the article.

Juan Jiménez Chacón: ponception and research design. He carried out the statistical processing and interpretation of the results. Participated as an analyst in the nested design. Manuscript review.

Manuel Álvarez Prieto: conception and research design. Manuscript review.