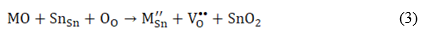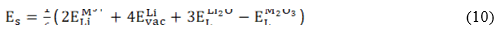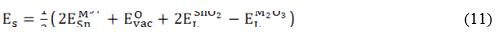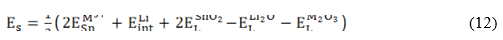Serviços customizados
Inglês (pdf)
Artigo em XML
Referências do artigo
Enviar este artigo por email
Citado por SciELO 
Similares em
SciELO 
Permalink
Introduction
In the context of a global transition to cleaner energy technologies, the design of safer, more durable energy storage devices constitutes an urgent research subject. Replacing the liquid electrolytes traditionally used in batteries with solid-state electrolytes (SSE) is a promising route to overcome existing issues associated with current liquid-electrolyte batteries, including flammability, leakages, and volatility. However, the development of inorganic SSE faces critical challenges, such as relatively low ionic conductivity as compared to conventional liquid electrolytes, interfacial resistance with the electrodes, and a narrow electrochemical window, which constrains their practical applications.1
Outstanding ion transport, recognized by high diffusion coefficients of the lithium ions and low activation energies, is an essential requirement of a material to be considered as an electrolyte for LIBs.1-5) Lithium stannate, Li2SnO3, is considered for many energy storage applications, including as an electrode, a inorganic solid electrolyte and a coating material for anodes in Li-ion batteries.5
Atomistic simulations based on density functional theory (DFT) and forcefield approaches have previously been used to explore the ground-state properties of undoped and doped Li2SnO3.3,4,6,7) Advanced atomistic simulations disclose additional information to experiment, related to revealing the migration mechanisms and energetics of dopant incorporation. Kuganathan et al.3) studied defect formation and ion migration in Li2SnO3 and showed that dopant with 4+ valence charge are the best dopants to be incorporated at the Sn4+ site in terms of lowering the formation energy.3 Al3+ as a dopant can also be used to occupy the Sn4+ site to increase the Li concentration in Li2SnO3 via Li interstitial defect compensation. The activation energy of Li-ion migration through various diffusion paths were also evaluated by using the conventional transition state theory.3
In our recent works, the defect formation energy and transport properties of transition metal dopant and pure divalent dopant were studied in two separated papers.6,7 Besides, the information collected in those manuscript are inaccessible for the majority of the researcher in the field living in developing countries. Collecting the main results of those manuscript, the aim of this work consists in the exploration of the ion transport properties and capabilities of Na- and K-doped Li2SnO3 as an inorganic solid electrolyte using advanced atomistic simulations. Defect formation and ion migration in Li2SnO3 systems are investigated, revealing the potential of Na- and K-doped Li2SnO3 as a promising inorganic solid electrolyte material.
Methodology
Lattice static calculations are performed using the GULP code.8 Interatomic potential parameters to model the ion interactions are taken from the literature.6,7 The Mott-Littleton approach is used for the defect calculations.9 This method subdivides the crystal structure into two spherical regions with radius r1 and r2 (with r1<r2), respectively. The isolated defect or defect cluster is located at the inner sphere r1, where the interaction between the defect/cluster with the local structure is strong. The external region r2 is treated by a quasi-continuum approximation.9 To the best accuracy of the defect energetics calculations, values of r1 = 13 Å and r2 = 21 Å are assumed after convergence testing. The Broyden-Fletcher-Goldfarb-Shanno algorithm was adopted to update the cell parameters and fractional positions during the defect energetics and geometry optimizations computations.8 This technique has been used to explore ion migration and defect formation in solid-state materials.6,7,10,11
LAMMPS code is used to determine the long-range diffusion of Li ions via potential-based MD simulations.12 The simulation boxes were created using a 5×5×4 supercell of Li2SnO3, equivalent to 4800 ions in the stoichiometric cell. The temperature range for MD simulations is 500-1 100 K. We consider two kinds of defective Li2SnO3 supercells; the first one contemplates the common Li2O Schottky defect and the second, the incorporation of divalent dopants as additional source of Li vacancies. The simulation boxes were first relaxed using an isothermal-isobaric ensemble (NTP) for reaching the equilibrium, the production runs were carried out with an isothermal-isochoric ensemble (NVT), while recording the mean square displacement (MSD) for the Li ions. The slope of the expected straight line of MSD plots was then used to calculate the diffusion coefficients (D) by the equation:
where t is the simulation time. Given the significant number of defect concentrations, each production run was limited to 2 nanoseconds (ns) with a time step of 2 faraseconds (fs).
Results and discussion
In order to disclose the transport properties, we consider various incorporation mechanisms: Li2O Schottky defect formation in pristine Li2SnO3, divalent dopant (M2+) at the Li -site with a Li -vacancy formation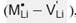 
, the substitution of M2+ at the Sn -site leading oxygen vacancy 
. For trivalent dopants (M3+) various incorporation schemes were considered, involving Li interstitial, and partial substitution of trivalent dopant at Li- and Sn- site leading Li and oxygen vacancies.(6,7)
The first mechanism describes Li2O Schottky defect formation in pristine Li2SnO3:
where LiLi is a Li -ion at a Li -site, OO is an O -ion at an O -site and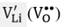 
represents a Li (O) vacancy. The second scheme represents the incorporation mechanism of a divalent dopant (M2+) at the Li -site with a Li -vacancy formation to ensure the charge neutrality:
where M Li • denotes a divalent dopant occupying a Li -site in Li2SnO3 lattice structure. Furthermore, the substitution of M2+ at the Sn -site is described by equation (3):
where 
represents a M2+-dopant at the Sn -site.
In this study, three incorporation mechanisms involve trivalent dopants (M3+) are additionally considered:
Equation (6) deals with M3+ substitution at the Sn-site occupying interstitial sites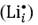 
in the structure. The solution (Es), binding (EB) and final solution (Ef) energies are computed accordingly. The solution energy (Es) for the defect energy for the Li2O Schottky defect is defined by equation (8):
where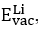 
, 
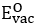and 
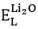represent the required energy for a Li (O) -vacancy creation (in eV/defect) and the lattice energies of Li2O (in eV/uc), respectively.
For the M2+ incorporation at Li- and Sn- site the relations are:
respectively. In equations (8) and (9)
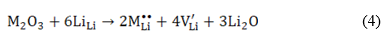, denote the M2+ substitution energy at the Li- and Sn- site (in eV/dopant) and , 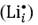the lattice energy of the MO and SnO2 oxides, respectively. In the case of trivalent dopant, the solution energy is given by:
where 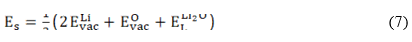denotes the M3+ substitution energy at Li -site, 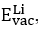at interstitial atomic position, at the Sn -site and the lattice energy of the M2O3 oxide considered.
Figure 1 depicts the results of defect energetics computations. For the Li2O Schottky defects, the formation leads to 2 eV/defect, which agrees with the reported values in the literature.(3,6,7) Solution energy varies from 1,84 to 2,80 eV/dopant for M2+ at the Li -site leading a Li vacancy. Mn2+, Sc2+ and Cd2+ have the lowest Es and Ef values. In this sense, these dopants are favorable to control the Li-vacancy concentration with low energetic cost. For the binding energy analysis, all EB values are negative, indicating the effective defect formation cluster relative to the incorporation mechanisms in concern.
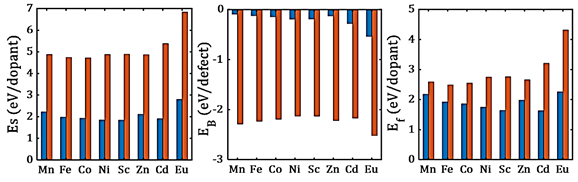
Fig. 1 Solution (Es), binding (EB) and final solution (Ef) energy of M2+ at a Li-site leading one Li-vacancy (blue bars) and M2+ at a Sn-site leading oxygen vacancy (brown bars), respectively
Figure 2 shows the defect energetic behavior for transition state dopant, specifically for 3+ charge state. Li- interstitial mechanism have lower ES and Ef, which indicates that trivalent dopants have a strong energetic preference for doping at the Sn-site, with a charge compensation from Li-interstitial formation. For binding energy, the values are similar to those obtained for divalent dopants.
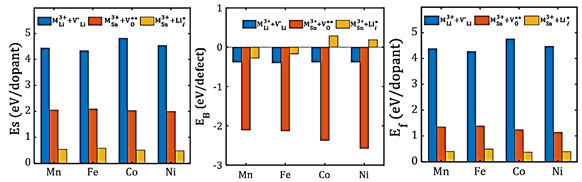
Fig. 2 Solution (Es), binding (EB) and final solution (Ef) energy of (blue bars) for transition metal dopant incorporation mechanisms. The legend depicts the pair defect involved
Inclusion of divalent dopant at Li site creates strong attractive interactions as compared to the repulsive Li-Li pair, while the interaction becomes even stronger for 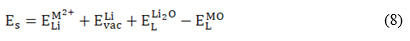. Fe2+, Co2+ and Zn2+ emerged as the best dopants to control the oxygen vacancy concentration, whereas Sc2+ and Cd2+ are good for tracking the Li-vacancy concentration in divalent doped Li2SnO3.
The transport properties of doped Li2SnO3 samples were evaluated.(6,7) Figure 3 displays calculated results of the Arrhenius-type dependence of diffusion and dc-conductivity for the specific divalent dopant samples. The results pointed out that the diffusion coefficient is higher in one or two orders of magnitude as compared to the non-doped sample where the Li-interstitial defect is involved.(7) In the latter case, transport properties of monocrystalline samples are exposed. The Li-interstitial mechanism leads to the highest diffusion coefficient as a consequence of a reduction of the average Li-Li distance, improving the Li-migration with smaller activation energy. As Co3+ and Mn3+ have the lowest Ea values upon charge state and relatively low final solution energy, both dopants can be considered to improve the transport properties as found in the resulting transition metal doped Li2SnO3 samples.
For pure divalent dopants, the corresponding transport properties, diffusion coefficient and dc-conductivity are also evaluated. For this set of divalent dopants, transport properties are evaluated for both mono- and nanocrystalline Li2SnO3 doped samples.6 The results are displayed in figure 4. As it is shown in figure 4, in monocrystalline divalent-doped Li2SnO3, the Sc2+, Zn2+, Cd2+ and Eu2+ dopants can result in a Li-ion diffusion/conduction improvement of over one order of magnitude in contrast to the pristine Li2SnO3 sample with low activation energies.7 The activation energy ranges between 0,40-0,44 eV and 0,34-0,38 eV for diffusion and conduction, respectively. Zn2+ is the best candidate to be used for improvement of the transport properties in monocrystalline Li2SnO3. A favorable reduction of the activation energy of 0,39-0,43 eV and 0,33-0,36 eV for diffusion and conduction, respectively, is observed. Activation energies are smaller in polycrystalline samples except for Zn2+ doped sample.6 These findings imply that Li ion transport properties can effectively be improved upon doping with divalent dopants, leading to better battery performance of polycrystalline samples.6,7
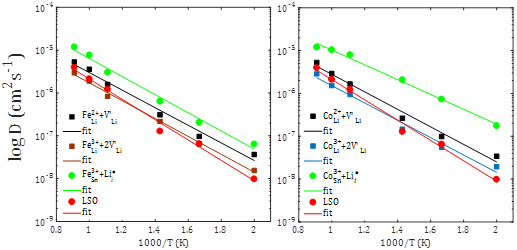
Fig. 3 Arrhenius plot of Li diffusion coefficient for each sample. LSO denotes the Schottky defect mechanism
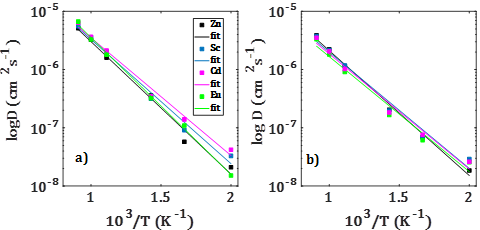
Fig. 4 Arrhenius dependence of a)-b) Li-ion diffusion coefficient (D) with the temperature (T) of mono- and polycrystalline M2+-doped Li2SnO3 (M2+ = Zn2+, Sc2+, Cd2+ and Eu2+) samples, respectively
Combination of calculated results of defect energetics and transport properties points out that inclusion of transition metal and pure divalent dopant into the Li2SnO3 structure effectively improves the quality of transport properties of Li2SnO3 with direct improvement for electrode/electrolyte in alkali ion batteries.6,7
Conclusions
We have utilized atomic-scale simulations to study dopant incorporation and Li -ion diffusion in pristine and metal doped Li2SnO3. Defect energy calculations reveal that divalent dopants occupies the Li site, leading to Li vacancy formation. In contrast, trivalent dopants have a strong energetic preference for doping at the Sn site, with charge compensation from Li -interstitial formation. Molecular dynamics simulations show that transition metal doped Li2SnO3 can result in a Li ion diffusion enhancement with lower activation energies. The activation energy for diffusion ranges between 0,34-0,42 eV, while the undoped value is 0,48 eV. In fact, trivalent states of transition metal dopant reduce the activation energy as compared with divalent state and undoped samples. Of particular interest, the interstitially Li containing samples have better transport properties as compared with the other samples. The values reported here are in line with those reported for other similar Li ion conductor compounds.
Based on the results of defect formation and transport properties explored in this work, we believe that divalent/trivalent doped Li2SnO3 can be proposed as a candidate material for electrodes and inorganic solid state electrolytes in alkali -ion batteries.
