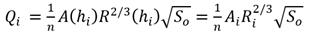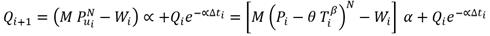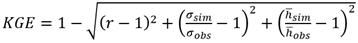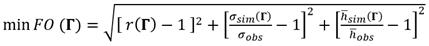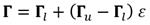Introducción
El acueducto de Albear es gestionado por la empresa Aguas de La Habana. Esta fuente de abasto a la capital cubana conduce volúmenes de agua de la cuenca subterránea Vento, a partir de dos importantes estructuras de captación de manantiales, denominadas Taza Grande y Taza Chica (figura 1).
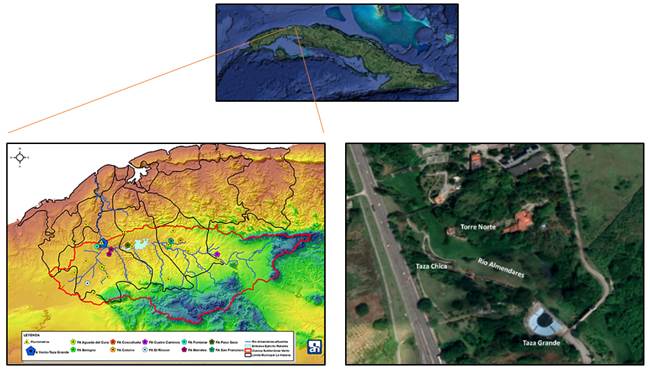
Figura 1 Ubicación geográfica y límites de la cuenca subterránea Vento. A la derecha, imagen satelital con las captaciones Taza Grande y Taza Chica
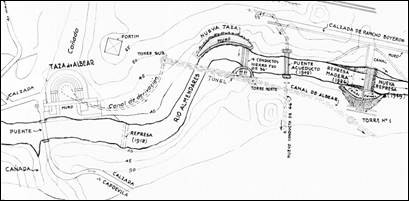
Las aguas son entregadas a un canal de derivación curvo en planta (figura 2), el cual sale de la esquina noroeste de la Taza Grande y conduce las aguas hasta dos sifones invertidos, ubicados en un túnel que cruza bajo el río Almendares desde la margen izquierda hacia la derecha, los cuales se encuentran conectados a un canal de sección ovoide (figura 3d) de 2,42 m de altura y 2,00 m de ancho máximo con una pendiente de fondo de 1:5000, contando con una sección de control ubicada en Torre Norte que permite estimar el caudal de descarga de los manantiales a partir de la medición de la profundidad de circulación.
 (Adaptado de: Fernández 1950)
(Adaptado de: Fernández 1950)Figura 2 Esquema en planta donde se muestra la ubicación de Taza Grande (Taza de Albear) y Taza Chica (Nueva Taza).
Antiguamente, al inicio del canal de Vento, los niveles eran medidos en la Torre Norte (figura 3a), con una regla graduada, tal y como se muestra en la figura 3c. Debido al notable deterioro de la regla graduada y a la necesidad de obtener mediciones confiables y precisas de los niveles a la entrada del canal, la empresa Aguas de La Habana implementó un sistema de adquisición de datos por medio de un sensor de nivel. Este sensor ultrasónico, marca FMU-232 (figura 3b), registra niveles en un rango entre 0 - 3,00 m, con una incertidumbre en la medición de 0,25 %, tal y como reporta Ossorio (2007).

Figura 3 a) Vista interior de Torre Norte, b) detalle de sensor ultrasónico de nivel FMU - 232, c) canal de Vento y antigua regla graduada, d) sección transversal del canal.
Las propiedades geométricas del canal de Vento han sido descritas en detalle por Pacho (1954), Alfonso (2008) y Martínez 2006, 2019a. Este último autor, a partir de dichas propiedades, realizó un análisis de las probables fórmulas empleadas por Albear para el diseño del canal de Vento, resultando que las evidencias apuntan a que la fórmula de Darcy permite verificar el valor de caudal de diseño reportado por Albear (1,20 m3/s), tomando en cuenta la confianza que le reportaba a este la mencionada fórmula (García, 2002 y Martínez, 2019a). Es válido destacar que existen importantes precedentes en la obtención de la curva de la sección de control en Torre Norte. En este sentido se encuentran las curvas de descarga obtenidas por Euler (1952), citado por Ossorio (2007) y Pacho (1954), aunque no está claro a partir de cuales ecuaciones de la hidráulica de canales fueron obtenidas, pues estas se encuentran disponibles bien en forma gráfica o tabular.
Martínez (2019a), aplicando la popular ecuación de Manning, y con el correspondiente análisis de la variación de la rugosidad en el tiempo, a partir de mediciones reportadas en la literatura en los años 1908, 1912, 1953, 1996 y 2005, demuestra las alteraciones que ha sufrido la curva de descarga del canal de Vento.
No obstante, la variabilidad del comportamiento de la profundidad de circulación en el canal de Vento, y por tanto, del caudal de descarga de las captaciones que lo alimentan, viene influenciada por las variaciones climáticas de la precipitación, como elemento fundamental de recarga, así como del patrón conductual de las extracciones en la cuenca subterránea Vento. En la Figura 4 se muestra el comportamiento histórico de dichas variables, así como de las profundidades de circulación entre enero/1987 y diciembre/2017. El régimen de explotación de las extracciones presenta una marcada tendencia creciente (Rivera, 2009; Méndez, 2017). En este sentido, la ecuación de Manning como modelo no depende directamente de estas variables, por lo que su carácter predictivo es limitado.
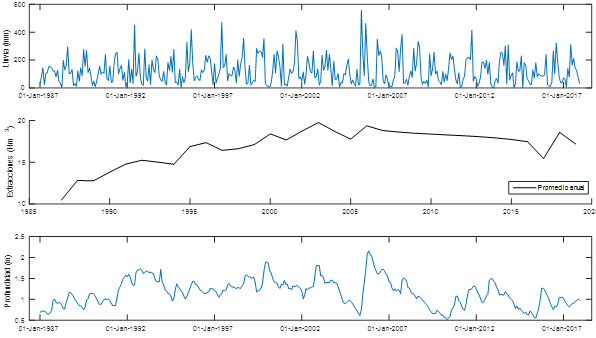
Figura 4 Comportamiento histórico de las precipitaciones y extracciones en la cuenca subterránea de Vento y su influencia en la profundidad del canal.
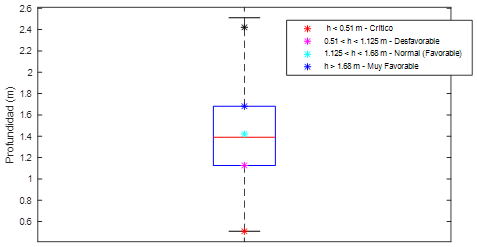
Es válido resaltar que los regímenes de operación del canal de Vento, a partir del análisis del comportamiento histórico de los niveles (profundidades de circulación), quedan representados en el diagrama de caja y bigotes de la figura 5, que permite mostrar valores medios y su dispersión. El rango normal de trabajo (1.125 - 1.68 m, percentil 25 y 75, respectivamente) fluctúa alrededor de la profundidad de diseño del canal de Vento (1.42 m, aprox., mediana de la serie histórica). Condiciones desfavorables para el abasto se encuentran en profundidades por debajo de 1.125 m y llegan a ser críticas para valores iguales o inferiores a 0.51 m.
El objetivo de esta contribución es, precisamente, proponer un modelo para realizar proyecciones mensuales de la descarga del canal de Vento que incorpore la influencia de las variables hidrológicas y de explotación de la cuenca, bajo diferentes condiciones de operación, para mejorar la gestión de los volúmenes que son entregados a los consumidores que se abastecen de este acueducto.
Modelo para estimar las descargas del canal de vento
Para monitorear las descargas del canal de Vento, la Empresa Aguas de La Habana registra las profundidades de circulación del canal de Vento. Esta medición continua se lleva a cabo mediante el sensor ultrasónico, con una frecuencia de muestreo de 10 minutos (Ossorio, 2007). Las propiedades geométricas de la sección de control del canal de Vento están debidamente determinadas (Martínez, 2019a) y la transformación de niveles a caudales de circulación se lleva a cabo utilizando como modelo la ecuación de Manning. El procesamiento y monitoreo de dichas descargas se realiza en el Centro de Operaciones de la empresa Aguas de La Habana a partir de su estimación (figura 6).
Tomando en cuenta que el régimen de trabajo del canal de Vento es continuo, y que durante los días de un mes las fluctuaciones en los niveles de circulación en el canal, como promedio, pueden ser despreciables, entonces para el i-ésimo mes (i = 1,2…) las descargas por el canal vendrán dadas por:
Donde:
N |
coeficiente de rugosidad de Manning (~ 0,012 en las condiciones actuales, según Martínez 2019a) |
H |
nivel de circulación (m) |
A |
área mojada (m2) |
R |
radio hidráulico (m) |
S o |
pendiente del lecho de fondo (1/5000) |
En esta contribución se propone correlacionar la precipitación, la temperatura y las extracciones mensuales en la cuenca Vento con la descarga de esta a través del canal. Para ello, se introduce el Modelo para el Estudio de Descargas de Acuíferos (M.E.D.A) del Instituto Tecnológico GeoMinero de España, el cual puede ser expresado como (Martínez, 2019b):
Siendo:
P u |
la lluvia útil (aprovechable) del i-ésimo mes, los parámetros M, N, θ y β de origen climático |
α |
coeficiente de agotamiento del acuífero |
P i , T i , y W i |
representan la precipitación (mm), la temperatura media ( o C) y las extracciones (m3) mensuales, respectivamente |
Δt i |
intervalo de tiempo (ej. 1 mes) |
Es válido destacar que, de acuerdo a la literatura consultada, el empleo de MEDA en Cuba tiene como referente principal el estudio de Martínez et al. (1986) para estimar las descargas del acuífero Ciego - Morón, en la provincia de Ciego de Ávila. Posteriormente, Martínez (2019b) retomó este mismo escenario y contrastó dicho modelo y varios similares. Hasta donde las evidencias lo permiten, se puede afirmar que no existen precedentes de que este modelo se haya aplicado con anterioridad en la cuenca Vento, lo cual refuerza su selección, sumado a su simplicidad de implementación computacional.
Influencia del embalse Ejército Rebelde en las descargas del canal de Vento
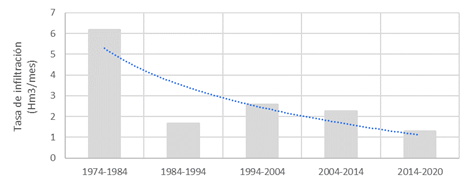
El embalse Ejército Rebelde, desde su puesta en operación en 1974, tiene la función de recargar al acuífero Vento. Sus tasas de infiltración están íntimamente relacionadas con las variaciones del volumen almacenado. Acorde con Rodríguez (2021), entre los años 1993 y 2020 los niveles mínimos anuales de la presa presentan una tendencia creciente, como constatación de que las infiltraciones hacia el acuífero Vento han ido disminuyendo como consecuencia del azolvamiento desde su construcción hasta la fecha. En la figura 7 se muestra la tasa promedio de infiltración decadal, con una tendencia marcadamente decreciente.
El comportamiento de esa tasa de infiltración representa entre un 5 ~ 10 % del volumen extraído en la cuenca Vento (~20 Hm3/ mes), lo cual quiere decir que, en periodo poco lluvioso (o sequía), esta tasa no es suficiente para contribuir a la recuperación en el balance de los recursos hídricos en la cuenca Vento. Por esta razón, dicha componente en la recarga no será considerada en esta contribución, lo cual equivale a razonar que, en las condiciones actuales, las variaciones en los niveles del canal de Vento son poco sensibles respecto a las variaciones de nivel en el embalse Ejército Rebelde.
Solución numérica del modelo
Las ecuaciones (1) - (2) forman un sistema a través del cual pueden estimarse descargas y niveles de circulación en el canal de Vento, conocido el comportamiento de las precipitaciones, temperaturas y extracciones en la cuenca Vento. Como ya se mencionó, este enfoque no ha encontrado precedentes en investigaciones realizadas por Alfonso (2008), Rivera (2009), Sánchez (2017) y Méndez (2017), consideradas de las más relevantes. Tomando en cuenta que es un sistema el cual, para su solución numérica debe partir de una condición inicial, existen dos alternativas de solución bien identificadas:
Se conoce el caudal en el estado inicial (Q i=1 = Q 1): en este caso se resuelve directamente la ecuación (2) para i =1,2,…y de esta manera se obtiene una serie de descargas Q 1, Q 1 … las cuales permitirán obtener mes a mes las profundidades de circulación mediante la aplicación de la ecuación (1), aplicando un método numérico de separación de raíces.
Se conoce el nivel en el estado inicial (h i=1 = h 1): sustituyendo la ecuación (1) en la ecuación (2) se obtiene:
De forma similar a la alternativa anterior, para resolver la ecuación (3), puede aplicarse un método numérico de separación de raíces y, de esta manera, se obtendría una serie de niveles mensuales h 1, h 2 … los cuales al ser evaluados directamente en la ecuación (1), permiten cuantificar las respectivas descargas en el canal de Vento.
Estimación de parámetros del modelo propuesto
El sistema de ecuaciones (1) - (2) involucra parámetros característicos del canal, así como aquellos que identifican a la cuenca Vento, de origen climático y del sistema acuífero. En sentido general, esto genera un vector de parámetros 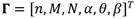 , los cuales son desconocidos “a priori” y que es preciso que sean estimados eficientemente para un satisfactorio desempeño del modelo que se plantea en esta contribución. Es válido destacar que el coeficiente de rugosidad del canal no será involucrado en este análisis, ya que este ha sido estimado con suficiente precisión en una contribución anterior por Martínez (2019a), y su valor de referencia es n = 0,012. De esta manera, el modelo propuesto es pentaparamétrico y dado el carácter empírico de su formulación conjunta, será considerado que no existe correlación entre los parámetros a ser estimados.
, los cuales son desconocidos “a priori” y que es preciso que sean estimados eficientemente para un satisfactorio desempeño del modelo que se plantea en esta contribución. Es válido destacar que el coeficiente de rugosidad del canal no será involucrado en este análisis, ya que este ha sido estimado con suficiente precisión en una contribución anterior por Martínez (2019a), y su valor de referencia es n = 0,012. De esta manera, el modelo propuesto es pentaparamétrico y dado el carácter empírico de su formulación conjunta, será considerado que no existe correlación entre los parámetros a ser estimados.
Para la estimación de parámetros en modelos hidrológico - hidráulicos, Gupta et al. (2009) y Kling et al. (2012) han introducido un índice conocido por eficiencia de Kling - Gupta (KGE, por su acrónimo en inglés), para resumir en dicho indicador el desempeño de los modelos. Este índice se define de acuerdo a la ecuación (4):
Siendo:
r |
coeficiente de correlación de Pearson |
σ |
es la desviación estándar |
|
la media de los valores simulados u observados, según corresponda. Cuando KGE = 1, se indica una coincidencia perfecta |
En este sentido, Knoben et al.(2019) demuestran que valores mayores que - 0,41 indican que el modelo mejora por encima del flujo medio como criterio de referencia. En el caso particular de esta aplicación, la variable simulada corresponde a niveles y el criterio de referencia sería el nivel medio del canal de Vento. Por tanto, con el objetivo de maximizar la eficiencia computacional del modelo se plantea minimizar la siguiente función objetivo:
Algoritmo de cómputo
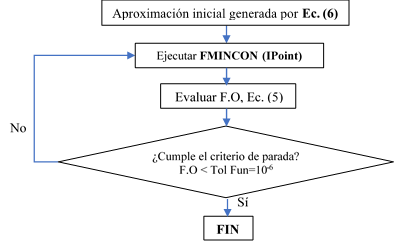
En esta investigación ha sido utilizado el algoritmo punto interior (en lo adelante IPoint), el cual le incorpora rapidez y precisión al problema abordado, al tratarse de minimizar la función objetivo (ecuación 5), sujeta a restricciones de los parámetros. El algoritmo se encuentra implementado en el toolbox de optimización del asistente matemático MatLab, a través de la función fmincon. En la figura 8 se muestra el diagrama de flujo para la estimación de los parámetros en el modelo propuesto. Para la aplicación de IPoint, inicialmente se genera una aproximación inicial aleatoria del vector de parámetros en la forma:
Nótese que 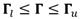 y
y 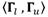 son los vectores de los respectivos límites inferior y superior de los parámetros del modelo; ε = número aleatorio uniformemente distribuido entre 0 y 1. El algoritmo IPoint se ejecuta y la función objetivo (ecuación 5) es evaluada y se compara con la tolerancia (criterio de parada, valor predeterminado en MatLab, TolFun =10-6). Este procedimiento se ejecuta sistemáticamente hasta que se cumple que el valor de la función objetivo sea menor que la tolerancia. De esta forma, quedan determinados los parámetros y la eficiencia del modelo.
son los vectores de los respectivos límites inferior y superior de los parámetros del modelo; ε = número aleatorio uniformemente distribuido entre 0 y 1. El algoritmo IPoint se ejecuta y la función objetivo (ecuación 5) es evaluada y se compara con la tolerancia (criterio de parada, valor predeterminado en MatLab, TolFun =10-6). Este procedimiento se ejecuta sistemáticamente hasta que se cumple que el valor de la función objetivo sea menor que la tolerancia. De esta forma, quedan determinados los parámetros y la eficiencia del modelo.
Estudio de caso
Para abordar el análisis de las descargas mensuales del canal de Vento serán contemplados dos periodos. El primero de ellos, correspondiente a la etapa de calibración, será de Mayo/1999 a Diciembre/2005, utilizado en una contribución anterior por Sánchez (2017). El segundo periodo seleccionado es para la etapa de validación, el cual contempla los meses de Enero/2014 a Diciembre/2016. Este último ha sido empleado por Bui (2019) en un análisis de los recursos extraídos en la cuenca Vento durante ese periodo.
Definición del área a modelar y datos para la estimación de la descarga
En el área en estudio, la descarga del acuífero al canal de Vento se produce por los manantiales que son captados por las estructuras Taza Grande y Taza Chica. Los niveles medidos en la sección del canal localizado en Torre Norte, se reportan en los periodos (Mayo/1999 - Diciembre/2005 y Enero/2014 - Diciembre/2016). En ambos, se dispone de datos diarios de precipitación en la red de estaciones pluviométricas del Instituto Nacional de Recursos Hidráulicos - INRH (P-12, P-15, P-35, P-166, P-282, P-284, P-293, P-303, P-338, P-340, P-341, P-342, P-343, P-451 y P-456), los cuales fueron procesados para el cálculo de la lluvia media mensual sobre la cuenca. A partir de los registros de la estación climática de Santiago de Las Vegas, correspondiente a la red de estaciones del Instituto de Meteorología - INSMET, se obtuvieron los datos de temperatura diaria, los cuales de forma análoga fueron procesados para obtener la temperatura media mensual. Los datos de extracciones de las obras de captación fueron suministrados por la Empresa “Aguas de La Habana”. En la figura 9 se encuentran las extracciones mensuales para los periodos antes mencionados.
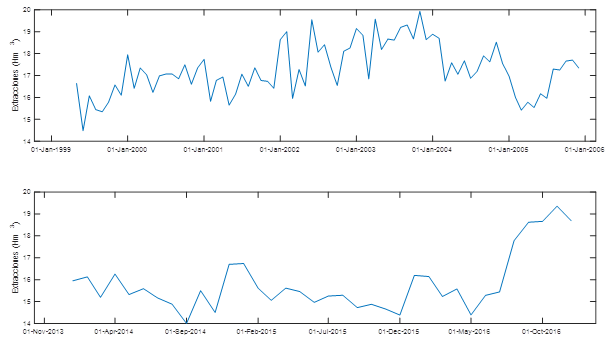
Figura 9 Extracciones mensuales en la cuenca subterránea Vento (superior: May/1999-Dic/2005, inferior: Ene/2014 - Dic/2016)
Experimento numérico
Para estimar los intervalos de los parámetros involucrados en el modelo propuesto, fue llevado a cabo un experimento numérico. El algoritmo IPoint, como ya se mencionó anteriormente, presenta una tolerancia Tol = 10-6, la cual está definida como el mínimo valor tolerable que puede obtener la función objetivo en estudio, dada en este caso por la ecuación (5). Las ejecuciones preliminares del mencionado algoritmo permitieron establecer los límites inferior y superior de cada uno de los parámetros, definiéndose de esta manera el espacio de búsqueda, con una dimensión igual al número de parámetros a ser estimados (Dim = 5), tal y como se muestra en la tabla 1.
Resultados y discusión
En la tabla 2 se muestran los parámetros que presentaron el mejor desempeño en la evaluación de la función objetivo dada por la ecuación (5). Se realizaron 10 corridas, siendo la de mejor eficiencia computacional la segunda réplica (tabla 2). Se detectó que el parámetro M exhibe las mayores variaciones con relación a su valor medio. Los de menor desviación fueron los exponentes N y (, con valores en el entorno de 2,20 y 1,40 respectivamente.
Tabla 2 Conjunto de parámetros del modelo para cada una de las réplicas ejecutadas
| Réplicas | M | N | ( | ( | ( | F.O(ec.5) | KGE (ec.4) |
|---|---|---|---|---|---|---|---|
| 1 | 209,7124 | 2,2329 | 0,0130 | 0,0437 | 1,4798 | 0,2880 | 0,7120 |
| 2 | 203,4458 | 2,2392 | 0,0135 | 0,0505 | 1,4350 | 0,2627 | 0,7373 |
| 3 | 218,6707 | 2,2258 | 0,0135 | 0,0542 | 1,4128 | 0,2659 | 0,7341 |
| 4 | 275,4428 | 2,1835 | 0,0135 | 0,0512 | 1,4308 | 0,2771 | 0,7229 |
| 5 | 211,8896 | 2,2316 | 0,0135 | 0,0587 | 1,3879 | 0,2641 | 0,7359 |
| 6 | 222,3654 | 2,2228 | 0,0135 | 0,0508 | 1,4330 | 0,2674 | 0,7326 |
| 7 | 288,5709 | 2,1652 | 0,0100 | 0,0597 | 1,3829 | 0,4550 | 0,5450 |
| 8 | 225,7425 | 2,2200 | 0,0135 | 0,0598 | 1,3821 | 0,2673 | 0,7327 |
| 9 | 292,8761 | 2,1721 | 0,0135 | 0,0548 | 1,4095 | 0,2810 | 0,7190 |
| 10 | 247,3278 | 2,2032 | 0,0135 | 0,0567 | 1,3987 | 0,2718 | 0,7282 |
| Media | 239,6044 | 2,2096 | 0,0131 | 0,0540 | 1,4152 | 0,29 | 0,71 |
| Cv | 0,1424 | 0,0122 | 0,0840 | 0,0941 | 0,0215 | - | - |
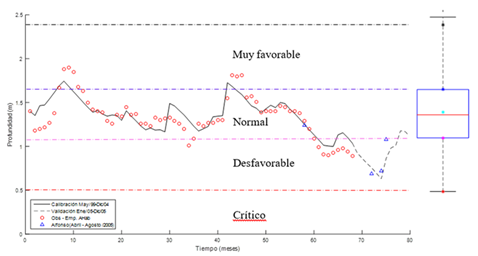
En la figura 10 puede apreciarse una notable convergencia entre los niveles observados y simulados en el canal durante el periodo Mayo/1999-Diciembre/2005 (80 meses en total), considerando el régimen de recarga neta a que fue sometida la cuenca Vento. Nótese que en dicho periodo el canal mantuvo predominantemente un comportamiento normal (71 % de duración del periodo), a excepción del periodo 2004-2005, donde existió una sequía importante que influyó negativamente en el régimen de trabajo del canal, cayendo en zona desfavorable. En este periodo de escasas precipitaciones predominó la influencia de las extracciones en los descensos de nivel registrados.
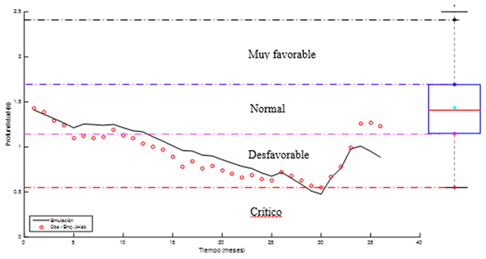
La validación del modelo propuesto en el periodo Enero/2014-Diciembre/2016 arroja también resultados satisfactorios (figura 11). En este caso el criterio de eficiencia del modelo KGE = 0,8776. Este fue un periodo caracterizado por un decrecimiento de los niveles en el canal de Vento, marcado por un desbalance en la recarga neta del acuífero producto de extracciones sostenidas y una disminución en los acumulados mensuales de precipitación. Esto originó que el canal operara en zona desfavorable entre los meses de Mayo/2014 - Septiembre/2016 (~ 80 % de duración del periodo), llegando a ser crítico el servicio durante los meses de Mayo-Junio/2015, donde la profundidad de circulación fluctuó alrededor del valor mínimo histórico.
Conclusiones
En la presente contribución se estimaron las descargas de los manantiales al canal de Vento a partir de un modelo propuesto por los autores. Este modelo fue implementado en el asistente matemático MatLab y acoplados al algoritmo IPoint, demostrándose la robustez de la estrategia abordada para reproducir series mensuales de caudales. Fueron identificados los parámetros relacionados con el volumen de precipitación drenado por el acuífero Vento y aquellos que caracterizan su agotamiento.
El desempeño del modelo caracterizado por las eficiencias computacionales alcanzadas, de acuerdo con el criterio de Kling -Gupta propuesto demostró ser totalmente satisfactorio al ser contrastado con las observaciones en la estación en el canal de Vento para los periodos analizados. Así mismo mostró gran adaptabilidad para diferentes escenarios de explotación y variabilidad de las precipitaciones.