ARTÍCULO ORIGINAL

 

 

Diseño Óptimo de Líneas de Aducción por Bombeo

 

Optimal Design of Pumped Water Pipelines

 

 

Carlos José Martins Alves ^I, José Bienvenido Martínez Rodríguez ^II

^I Universidad Nacional Experimental Francisco de Miranda (UNEFM).
^II Centro de Investigaciones Hidráulicas. Instituto Superior Politécnico José Antonio Echeverría (Cujae). La Habana.

 

 

---

RESUMEN

El uso de técnicas de optimización en el diseño de sistemas de abastecimiento de agua potable ha avanzado en los últimos años. No obstante, la complejidad de estos algoritmos ha impedido su uso general en la práctica. En este trabajo se desarrolló un algoritmo para el diseño óptimo de líneas de aducción por bombeo que determine el número, capacidad y ubicación de las estaciones de bombeo requeridas, aplicando un algoritmo de programación dinámica. Se divide la línea de aducción en tramos con una estación de bombeo probable al inicio del tramo. El algoritmo calcula los costos de inversión y energía de cada posible diámetro en cada tramo. La alternativa seleccionada es la del costo mínimo total. Para verificar el algoritmo, se empleó un caso de la literatura optimizado por una técnica de Colonia de Hormigas, obteniéndose similitud en sus resultados.

Palabras clave: líneas de aducción, diseño óptimo, programación dinámica.

---

ABSTRACT

The use of optimization techniques in the design of water supply systems has advanced over the years. However, complexity of these algorithms has prevented its general use in practice. In this study an algorithm was developed for the optimal design of pumped water mains including determination of number, capacity and location of required pumping stations, applying a dynamic programming algorithm. The pipeline is divided in sections with a probable pumping station at the beginning of each section. The algorithm calculates capital and energy costs for each possible diameter for every section. The chosen alternative is the one with minimum total cost. To verify the proposed algorithm a case of the literature optimized with a model of Ant Colony was tested which produced similar results.

Keywords: water pipelines, optimal design, dynamic programming.

---

 

 

INTRODUCCIÓN

La infraestructura usada para el transporte del agua desde las fuentes a los centros de consumo son las líneas de aducción (también llamadas conductoras). Desde el punto de vista de su funcionamiento hidráulico estas líneas pueden ser por gravedad o por bombeo. En el caso de las aducciones por gravedad su diseño resulta sencillo, puesto que el diámetro mínimo a colocar (desde el punto de vista económico, el diámetro que genere el menor costo de ejecución del proyecto) está definido como el que aproveche al máximo el desnivel existente entre el inicio y el fin de la conducción, esto es, que equipare las pérdidas de carga con el desnivel existente. En las aducciones por bombeo esto no es así, ya que entran en juego otra serie de factores que hacen más complicado hallar el diseño de costo mínimo. Entre estas consideraciones están los costos de los equipos de bombeo, costos de la infraestructura relacionada con dichos elementos, costos de energía y otros.

Históricamente el procedimiento para el diseño ha sido por ensayo y error, es decir, los proyectistas calculan algunas alternativas modificando unas pocas variables (generalmente diámetros), obteniendo así un diseño particular, que generalmente es función de la experiencia de cada proyectista en particular (Simpson et al. 1994). Sin embargo, tomando en cuenta la gran variedad de componentes del sistema, y si todos ellos se modifican, se podría concluir que hay muchas alternativas de solución que no se toman en cuenta, pudiendo ser alguna de ellas la óptima (la más económica).

En las últimas décadas, ha cobrado importancia la aplicación de técnicas de optimización al diseño de sistemas de abastecimiento, por una parte debido a que los costos de las tuberías representan el 70% de los costos de tales sistemas (Jung and Karney 2004), y por otra, debido a que los recursos económicos son escasos en los países en vías de desarrollo, lo que obliga a ser eficiente en su inversión.

Sin embargo, Formiga et al. (2006) indican que el dimensionamiento optimizado de sistemas de abastecimiento ha originado centenas de trabajos científicos en las últimas décadas, sin embargo la mayoría de las metodologías desarrolladas no llegan a ser aplicadas en la práctica. Esta última idea plantea entonces la necesidad de búsqueda de algoritmos más amigables que permitan de forma sencilla su programación a fin de que puedan permear al campo práctico y realmente aportar beneficios en los proyectos a ejecutar.

FORMULACIÓN Y DESARROLLO DEL MODELO PROPUESTO

Planteamiento del modelo

El problema planteado en este trabajo consiste en adaptar una técnica de optimización a fin de poder obtener para una línea de aducción sus diámetros óptimos (que minimicen los costos de proyecto), pero a su vez que también indique la cantidad de estaciones de bombeo, en caso de ser requeridas, su ubicación y potencia, a fin de optimizar el diseño y minimizar los costos totales de proyecto.

Como se sabe, las líneas de aducción pueden estar formadas básicamente por tuberías y estaciones de bombeo. En las secciones de tuberías se deberá cumplir con lo expresado en la ecuación simplificada de energía, ecuación (1).

donde:

Pa y Pb = Presiones en el punto inicial y final del tramo de la conducción en estudio,

expresadas en Pascal.

γ = Peso específico del fluido en N/m³.

Va y Vb = Velocidades medias en el punto inicial y final de la conducción en m/s.

Za y Zb = Altura de los puntos respecto a un nivel de referencia en m.

g = Aceleración de la gravedad en m/s².

hp = Presión de bombeo impartida al fluido en m.

hf = Pérdidas de carga en m.

Las pérdidas de carga se pueden expresar por la ecuación (2) de Hazen Williams.

donde:

hf = Pérdida de carga en m.

Q = Caudal de circulación expresado en m³/s.

C = Coeficiente de rugosidad de Hazen Williams (adimensional), referente a la tubería.

D = Diámetro interior de la tubería en m.

L = Longitud de la tubería, m.

Por otro lado, los costos de adquisición e instalación de las tuberías estarán dados por la ecuación (3).

Puede apreciarse que en el caso de líneas de aducción con funcionamiento por gravedad el diámetro mínimo a colocar solo será función de la energía total disponible, la cual deberá igualarse a las pérdidas de carga. Sin embargo, esto no garantiza que la solución sea la más económica, porque para poca energía disponible generará requerimiento de grandes diámetros lo que pudiese producir una solución antieconómica. Se puede concluir que existirá una energía disponible crítica en la cual el sistema por bombeo y por gravedad tengan el mismo costo. En ese caso, si la energía disponible es mayor que la crítica el sistema por gravedad sería la solución y en caso contrario la solución sería por bombeo.

En el caso de la conducción con funcionamiento por bombeo, la energía adicional que se requerirá aportarle al fluido será proporcionado por las estaciones de bombeo, y su potencia expresada en kilovatios (kW) estará dada por la ecuación (4).

donde:

γ = Peso específico del fluido en kN/m³.

Q = Caudal expresado en m³/s.

H = Altura de bombeo en m.

ε = Eficiencia.

Estando la energía requerida asociada directamente al caudal transportado y a la altura total de bombeo, si se mantiene constante el caudal, el factor que incide es la altura de bombeo, la cual a su vez está comprendida por el desnivel a vencer y las pérdidas de carga en la conducción.

Y los costos asociados a la energía consumida por el equipo, estarán dados por la ecuación (5).

Obviamente al variar los diámetros, las pérdidas de carga variarán, y los costos de energía también cambiarán, lo que indica que existirán muchas alternativas de solución, cada una con un costo de implementación diferente. Por otro lado, si se varía la ubicación de la estación de bombeo y el número de estaciones de bombeo a emplear, el número de alternativas de solución se incrementa haciendo necesaria la aplicación de alguna técnica de optimización para ayudar en la selección de la solución óptima.

Para cualquier línea de aducción, sin importar su tipo de funcionamiento (por bombeo, por gravedad o mixta), si se supone dividida en «n» tramos continuos y numerados consecutivamente, el costo anualizado total de la mejor alternativa de solución a dicha aducción se obtendrá de minimizar (Afshar and Madadgar2011) la ecuación (6).

donde:

CCA = Costo anualizado total de la alternativa.

FRC = Factor de recuperación de capital, adimensional.

Cbom = Costo del equipo de bombeo.

Cest = Costo de construcción de la infraestructura civil de la estación de bombeo.

Cequip = Costo del equipamiento mecánico y de accesorios de la estación de bombeo.

Cele = Costo de la instrumentación eléctrica de la estación de bombeo.

Cenergía = Costos anuales de operación debido a los requerimientos energéticos.

Todo esto sujeto al cumplimiento de las siguientes restricciones:

1) Ecuación (7) de continuidad en cada nodo.

donde:

Q_tramo = Caudal que circula en el tramo, m³/s.

Q_ES = Caudal de entrada o salida en el nodo aguas abajo del tramo, m³/s.

Q_tramo-1 = Caudal que circula en el tramo siguiente, m³/s.

2) Ecuación (8) de la conservación de la energía en cada tramo.

donde:

Piezo_Abajo = Cota piezométrica aguas abajo del tramo en m.

Piezo_Arriba = Cota piezométrica aguas arriba del tramo en m.

Δ_Arriba-Abajo = Diferencia de cotas entre aguas arriba y aguas abajo del tramo en m.

AltBom = Carga por bombeo en m.

hf = Pérdidas de carga generadas en el tramo en m.

3) Límites de presiones en cada nodo, ecuación (9).

donde:

P_mín = Presión mínima permisible en m.

P_max = Presión máxima permisible en m.

4) Límites de velocidades en cada tramo, ecuación (10).

donde:

V_mín = Velocidad mínima permisible de circulación en m/s.

V_tramo = Velocidad de circulación en el tramo en m/s.

V_máx = Velocidad máxima permisible de circulación en m/s.

5) Límites de carga por bombeo en cada nodo, ecuación (11).

donde:

AltBom_mín = Altura mínima permisible de bombeo en m.

AltBom_máx = Altura máxima permisible de bombeo en m.

6) Disponibilidad de diámetros para cada tramo, en la forma de una lista de diámetros comerciales posibles.

Desarrollo del modelo

El desarrollo del modelo de optimización se basó en la programación dinámica, la cual tiene la ventaja de adaptarse mucho más fácilmente a este problema, por encima de otras técnicas determinísticas. Siendo esto así, quedará establecida la relación recurrente que identifica la política óptima para una etapa «n», dada la política óptima para la etapa anterior como expresa la ecuación (12), una ecuación clásica de la programación dinámica.

donde:

f_n*(s) = Costo inmediato (etapa n) + costo futuro mínimo (etapas n-1 en adelante).

s = Estado inicial en la etapa actual.

C_(s,xn) = Costo de opción de ir desde el estado inicial s al destino x_n al final de la etapa.

f_n-1*(x_n ) = Costo futuro mínimo desde la etapa final hasta el estado x_n.

El esquema general de trabajo consistirá, en primer lugar, en dividir el recorrido que tendrá la línea de aducción en tramos, de manera de ir segmentando el problema general en varios problemas de menor magnitud y esto se hará ajuicio del diseñador, tratando que la pendiente sea razonablemente constante para cada tramo, para que las elevaciones de la superficie sean preservadas en la segmentación (Martin 1990). De no cumplirse esto se podrían perder puntos significativos del perfil (puntos máximos altos y máximos bajos) que generarían afectación en el diseño final de la conducción. Estos tramos una vez definidos serán llamados las etapas del problema, es decir el problema de diseño tendrá tantas etapas como tramos se hayan definido.

Los estados de cada etapa serán definidos como las condiciones posibles en lasque se puede encontrar el sistema en cada etapa (sabiendo que el sistema es la línea de aducción en funcionamiento). La cota piezométrica, con la que llega el fluido a cada etapa, será el estado que esta pueda tomar y será función directa delos diámetros elegidos o probados; así se garantiza que el punto de conexión de una tubería con otra (la conexión de una etapa con la etapa siguiente) tenga la misma cota piezométrica. Al inicio y al final de cada etapa se tendrá un rango de valores que pudiese tomar la cota, y la pendiente que tome la línea piezométrica será función del diámetro que se esté probando para dicha etapa.

Se puede apreciar que la incógnita más importante es el diámetro a usar en cada etapa (conociendo el diámetro a colocar se obtienen las pérdidas), de ahí que se tome que la variable de decisión para cada etapa será el valor de la cota o altura piezométrica al inicio de la etapa anterior «n», que se conecta con el final de la etapa actual «n-1»; ya que el valor de la piezométrica al final de la etapa actual deberá coincidir con el valor inicial de la piezométrica de la etapa anterior, a fin de mantener la continuidad.

La ecuación recurrente (12) se irá aplicando etapa por etapa de atrás hacia adelante (desde aguas abajo hacia aguas arriba del modelo), calculando la política óptima de decisión para cada estado en cada etapa hasta llegar a la etapa inicial, tal como se puede mostrar en la figura 1.

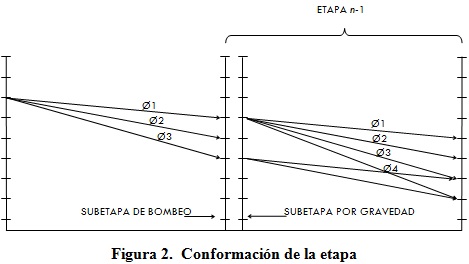
Se puede notar que, dentro de la formulación matemática del modelo, se da la posibilidad de ubicación de estaciones de bombeo en el recorrido de la línea de aducción, y para tomar esto en cuenta, se establecerá que la ubicación tentativa de las estaciones estará en el punto inicial de cada etapa. Siendo esto así, y para diferenciar los requerimientos de datos de la ecuación de estimación de los costos de implementación (ecuación 6), se establecerá que toda etapa tendrá asociada una subetapa por bombeo, quedando las etapas del modelo descritas por subetapas de tuberías (llamadas subetapa por gravedad) y subetapas por bombeo. Por lo tanto, cada etapa estará conformada por la superposición de los valores delos posibles estados de la subetapa por bombeo y de la subetapa por gravedad, según lo muestra la figura 2.

Cada una de las divisiones que poseen las etapas por bombeo y por gravedad, representa el valor que puede tomar la piezométrica. La diferencia que posea la piezométrica entre el inicio y el fin de la etapa, serán las pérdidas de carga y con ellas se podrá determinar un diámetro que las genere, quiere decir entonces, que cada piezométrica en la etapa por gravedad estará asociada a un diámetro, y este a su vez tendrá un costo de implementación. La determinación de los costos y su comparación, se hará en función de los costos anualizados de infraestructura requerida por cada alternativa y los costos energéticos requeridos por dicha infraestructura.

Así pues, se determinarán los costos para todas las alternativas de llegada de la piezométrica en el tramo aguas abajo, asociadas a un punto de partida aguas arriba, y como expresa la ecuación recurrente, se seleccionará el valor más bajo que resulte de la sumatoria del costo de implementación de dicho diámetro más el costo óptimo que conecta la piezométrica de la etapa «n-1» con la etapa «n». Este proceso se repetirá para todos los valores de piezométrica que estén disponibles aguas arriba en la etapa por gravedad.

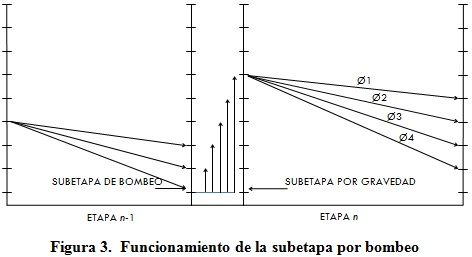
Una vez concluido el procedimiento de la etapa por gravedad, se procederá a determinar los costos a cada posible alternativa de la etapa por bombeo, la cual será necesaria para suplir la necesidad de energía a todas las posibles soluciones de la etapa «n-1», cuya piezométrica esté por debajo del nivel de partida de los estados en la etapa «n», según se aprecia en la figura 3.

Como se puede apreciar en la figura 3, en la subetapa por bombeo se comienza desde el valor mínimo que puede tener la piezométrica, y comienzan a determinarse los costos de bombeo para cada una de las posibles alturas que tenga la piezométrica en la subetapa por gravedad, seleccionando el valor que resulte mínimo de la sumatoria del costo de implementación de la etapa por bombeo más el costo óptimo general hasta el final, ya alcanzado en la etapa por gravedad. El procedimiento se repite para cada uno de los valores de la subetapa por bombeo, hasta completar todos los estados o hasta completar un rango especificado por el diseñador, en caso de que requiera limitar las alturas de bombeo.

La superposición de ambas matrices, generará una matriz única por etapa que servirá de referencia para la llegada de las piezométricas para la etapa siguiente, ya que en ella estarán almacenados los costos de soluciones óptimas generales obtenidos hasta el momento.

Este proceso se irá repitiendo etapa tras etapa, hasta llegar al tramo inicial de la conducción y donde a través de la matriz de la etapa, se obtendrá el costo óptimo total de la conducción. A partir de ahí se comienza un proceso inverso (desde aguas arriba hacia aguas abajo), donde con la información de la matriz de etapa, se obtiene la información en cuanto al diámetro óptimo para la etapa actual, además del punto de partida de la piezométrica y su punto de llegada, si se requiere bombeo y cuál será su altura. Así sucesivamente, se va obteniendo la información de cada tramo hasta que llegar al punto final de la conducción, quedando de esta forma definida la configuración óptima para la aducción.

PRUEBA DEL MODELO PROPUESTO

Para verificar la eficiencia del algoritmo planteado, se realizó el diseño para la conducción propuesta por Afsharand Madadgar (2011), para la cual determinaron la configuración óptima aplicando un algoritmo de optimización basado en Colonia de Hormigas, y se compararon sus resultados obtenidos con el modelo de optimización propuesto en este trabajo, usando la técnica de la programación dinámica, a fin de verificar la calidad de los resultados optimizados.

El perfil de la conducción es mixto (incluye tramos con funcionamiento por gravedad y por bombeo) y puede apreciarse en la figura 4.

En cuanto a las consideraciones hidráulicas en el diseño, se tomó como base lo establecido por Afsharand Madadgar (2011) en su trabajo de optimización, el cual consiste en aceptar que el gasto de circulación será 0,30 m3/s; los rangos de velocidad permisible en la conducción estarán comprendidos entre 0,40 y 2,60 m/s. Así mismo, el rango de valores de diámetros disponibles de acuerdo con el gasto circulante estará entre 0,40 m y 0,80 m, constituyendo 9 variables discretas. Los rangos disponibles de presiones máximas y mínimas a ser soportadas por las tuberías, estarán comprendidos entre 3 y 150 metros de columna de agua (mca), y la altura máxima de bombeo será establecida en 80 mca.

El coeficiente de fricción «C» para la ecuación de pérdidas de carga toma un valor de 120; además se tomó del mismo trabajo una vida útil del proyecto de 20 años y la tasa de interés de 10%. El costo del kilowatt-hora (kWh), al no ser aportado, se estableció en 0,07 dólares.

La aplicación del algoritmo programado en Visual Basic para aplicaciones (Macro para MsExcel) al modelo de prueba se realizó en diversas oportunidades, a fin de verificar la sensibilidad del modelo matemático a la variación de diversos parámetros. En primer lugar, se ejecutó el algoritmo programado con los valores de los parámetros señalados anteriormente, pero tomando en consideración que se seleccionará el mayor diámetro comercial más cercano, siempre que la diferencia entre el mayor diámetro comercial y el teórico se encuentre dentro de un rango equivalente al 90% de la diferencia entre el mayor y menor diámetro comercial más cercano. Esta diferencia se denomina aquí «ventana». Así mismo, se tomó como un (1) metro el valor del paso en la variación de la discretización de la piezométrica.

Los resultados obtenidos después de un tiempo de cálculo de 40,91 segundos, pueden apreciarse en la tabla 1, y la configuración óptima obtenida tiene un costo de implementación de 163960 Unidades Monetarias (U.M.), mientras que el óptimo del modelo de la literatura fue de122710 U.M.

Se puede apreciar también en la tabla 1, que los puntos óptimos para la ubicación de las estaciones de bombeo coinciden, así como la altura de bombeo combinada de las estaciones es muy similar, para el caso reportado en la literatura es de 137,03 m, mientras que para el obtenido por el algoritmo propuesto es 139 m.

En la figura 5, puede apreciarse el comportamiento de la línea piezométrica a lo largo de toda la conducción, pudiéndose observar que se garantiza cumplir con las presiones máximas y mínimas impuestas para todo el modelo, siendo además prácticamente igual a la obtenida por Afshar y Madadgar (2011). Desde el punto de vista económico no se puede realizar una comparación ya que para el modelo de referencia no fue aportado el costo del kWh, por lo que para la ejecución del programa se tomó el valor antes indicado.

Es notorio que, al ser la piezométrica una variable discreta y no continua, dentro de la formulación bajo programación dinámica, se ocasiona un error al estimar las pérdidas de carga con los diámetros comerciales, lo que genera que la piezométrica real de la conducción difiera de la piezométrica que estima el modelo matemático. Para evidenciar esto, se determinó la piezométrica para toda la conducción con los diámetros obtenidos del modelo matemático y se comparó con la ofrecida por el mismo modelo, obteniéndose que la diferencia llega a ser de hasta 1,27 metros, que la tiene la piezométrica real por debajo de la teórica en el nodo final de la etapa 17 (la última).

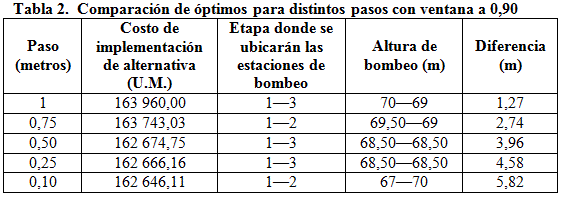
Posteriormente, se aplicó el algoritmo pero variando el grado de discretización para valorar como incide en la obtención de otras soluciones óptimas. Para ello, se evaluaron los valores de discretización con pasos a 0,75, 0,50, 0,25, y 0,10 metros, obteniéndose los resultados mostrados en la tabla 2.

Puede apreciarse que a medida que disminuye el paso en la discretización, se incrementa el error dado por la diferencia entre la piezométrica teórica y la real, y para el caso de discretizar la piezométrica cada 0,10 metros el error es de 5,82 metros en la descarga, es decir, la piezométrica real estará 5,82 metros por debajo de la teórica.

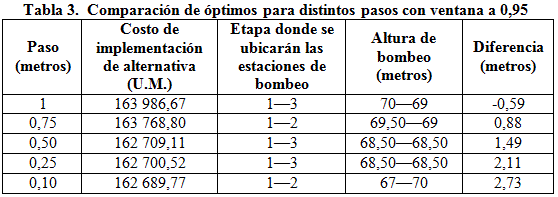
En función de los resultados anteriormente obtenidos, se varió el parámetro referente a la ventana para la aproximación de diámetros y se incrementó a 0,95; efectuadas las corridas al modelo se obtuvieron los resultados mostrados en la tabla 3.

Se puede apreciar, que los costos de implementación de alternativa se incrementan un poco en relación con los hallados para una ventana de selección de diámetro de 0,90, pero el error de la piezométrica se reduce.

Así mismo, se mantiene la tendencia de disminución de alturas de bombeo a medida que decrece el paso en la discretización de la piezométrica.

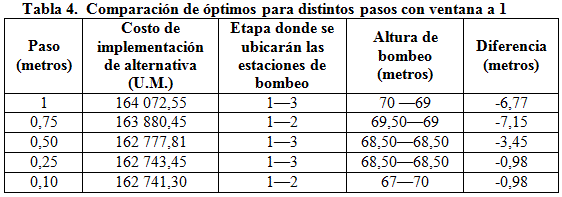
Para seguir ahondando en ello, se procedió a generar una nueva serie de corridas del modelo pero con una ventana de selección de diámetros igual a 1, es decir, el diámetro teórico se aproximará siempre al comercial mayor más cercano a este, para lo cual se obtuvieron los resultados siguientes, mostrados en la tabla 4.

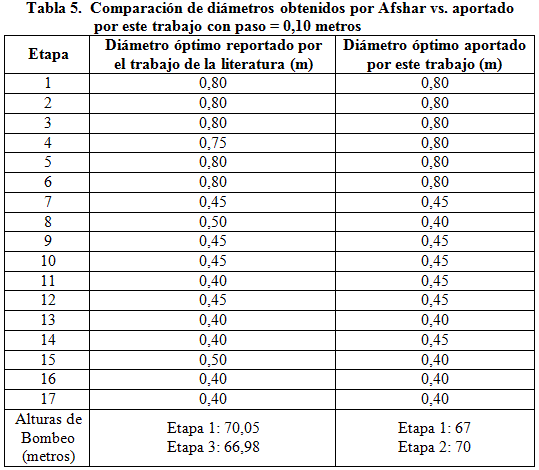
Puede evidenciarse, que la solución óptima factible de menor costo estará dada por escoger una ventana de 1, con valor de discretización de paso a 0,10 metros, para lo cual se obtiene un costo de implantación de 162741,30 U.M. y una altura de bombeo combinada de 137 metros, ubicando las estaciones de bombeo en el inicio de las etapas 1 y 2; quedando la configuración de diámetros establecida según lo mostrado en la tabla 5.

Así mismo, si se recalculan los costos de la solución aportada por Afsharand Madadgar (2011), tomando como base una tasa de interés de amortización de 10% y el costo de electricidad de 0,07 $/kWh; se observa que el costo anualizado es de 162784,75 U.M., el cual resulta más alto que el aportado por el modelo propuesto bajo programación dinámica, que asciende a 162741,30 U.M., y esto constituye una diferencia de 0,03 % a favor del modelo propuesto, significando esto una mejora en la solución en comparación con el algoritmo basado en Colonia de Hormigas.

 

CONCLUSIONES

· Se pudo constatar que los avances por generar procesos de optimización en los sistemas de abastecimiento por diferentes técnicas han sido muy grandes, sin embargo, la mayoría de las metodologías desarrolladas no son fáciles de implementar en la práctica.

· Por otro lado, la aplicación del algoritmo al modelo de prueba de la literatura, verificó que con la creación de la subetapa por bombeo y la subetapa por gravedad dentro de cada etapa de la formulación por programación dinámica, se le da solución al problema de ubicación óptima de las estaciones de bombeo necesarias para un diseño de aducción, sin importar las características del perfil.

· Así mismo, se observó que a medida que se disminuye el paso en la discretización de los valores de la piezométrica, se logran soluciones más económicas; y para los pasos más bajos se obtienen los valores menores de error, al comparar la piezométrica aportada por el modelo contra la real.

· De acuerdo con las modelaciones efectuadas, resultó recurrente que la solución óptima factible siempre estará dada por una ventana de aproximación de diámetros de 1, por lo tanto, deberá siempre aproximarse el diámetro teórico al comercial mayor más cercano, para el modelo desarrollado.

 

 

REFERENCIAS BIBLIOGRÁFICAS

1. Afshar A. and Madadgar, S. «Forced water main design; mixed ant colony optimization». International journal of optimization in civil engineering, 1, 24-71, Publisher: Building & Housing Research Center, School of Civil Engineering, Iran University of Science and Technology, Teheran, Iran, (2011).

2. Formiga K., Chaudhry F., y Vieria, M. «Otimizacao multiobjetivo de redes de abastecimiento de agua». Paper presented at the VI SEREA - Seminario Iberoamericano sobre sistemas de abastecimiento urbano de agua, Brasil, (2006).

3. Jung B. and Karney B. «Fluid transients and pipeline optimization using GA and PSO». Urban water journal, 1:2, 167-176, London, United Kingdom, (2004).

4. Martin Q. «Linear water supply pipeline capacity expansion model». Journal of hydraulic engineering, 116:5, 675-691. ASCE. USA, (1990).

5. Simpson A., Dandy G., and Murphy L. «Genetic algorithms compared to other techniques for pipe optimization». Journal of water resources planning and management, 120:4, 423-443. ASCE. USA, (1994).

 

 

Recibido: 17 de septiembre de 2014.
Aprobado: 13 de diciembre de 2014.

 

 

Carlos José Martins Alves, José Bienvenido Martínez Rodríguez, Universidad Nacional Experimental Francisco de Miranda (UNEFM), Centro de Investigaciones Hidráulicas. Instituto Superior Politécnico José Antonio Echeverría (Cujae), La Habana, e-mail: [e-mail], email: [e-mail]