ARTÍCULO ORIGINAL

 

 

Relación entre tiempo de consolidación y permeabilidad no saturada en presas de tierra

 

Relationship between strain rate and unsaturated permeability for earth dams

 

 

Jenny García Tristá,^I Willian Daniel CobeloCristiá,^I Gilberto Julio Quevedo Sotolongo,^II

^I Facultad de Ingeniería Civil,Instituto Superior Politécnico José Antonio Echeverría (Cujae), La Habana. Cuba.
^II Facultad de Construcciones, Universidad Central «Marta Abreu» de Las Villas (UCLV), Santa Clara, Cuba.

 

 

---

RESUMEN

Las limitaciones de la Mecánica de Suelos tradicional son evidentes cuando se necesita explicar las deformaciones en suelos no saturados, es por ello que en este trabajo se presenta la obtención de la variación del tiempo de consolidación cuando varía la permeabilidad del suelo debido a cambios en el grado de saturación, empleándose en el análisis el modelo de Rojasy Alanís para la obtención de la velocidad de deformación y los modelos de Van Genuchteny Fredlundpara la obtención de la curva de conductividad hidráulica en el suelo no saturado de la formación Capdevila, a partir de la curva de retención, tomando como caso de estudio una presa de tierra de 22m de altura.

Palabras clave: conductividad hidráulica, curva de retención,permeabilidad, suelos no saturados, tiempo de consolidación.

---

ABSTRACT

The limitations of traditional Soil Mechanics are evident when you need to explain the deformation in unsaturated soils. That is why in this paper is presented how to obtain the time variation of consolidation when soil permeability varies due to changes in the degree of saturation. In the analysis Rojas and Alanísmodel is applied to obtain the strain rate and Van Genuchtenand Fredlundmodels are applied to obtain the hydraulic conductivity curve in the Capdevila formation unsaturated soil sample, starting from the retention curve. The case study presented is a 22m highearth dam.

Key words: hydraulic conductivity, retention curve, permeability, unsaturated soils, time of consolidation.

---

 

 

INTRODUCCIÓN

Las limitaciones de la Mecánica de Suelos tradicional son evidentes cuando se necesita explicar las deformaciones en suelos no saturados o de las estructuras apoyadas en esos suelos (pavimentos, presas de tierra, taludes, cimentaciones entre otros) sujetos a cargas de servicio o en los estados de tensiones totales presentes in situ, donde la deformación que sufre un suelo al aplicarle un esfuerzo depende de la composición, de la relación de vacíos, de la historia tensional y de la forma en que se apliquen los esfuerzos.

Al diseñar una presa hay que tomar en consideración el comportamiento tenso-deformacional de los suelos que la conforman, teniendo en cuenta la curva de compresibilidad del suelo mediante el ensayo de consolidación, donde para suelos arcillosos que tienen una baja permeabilidad la deformación va a depender del tiempo.

La formación Capdevila es una formación geológica muy abundante en las provincias occidentales de Cuba y ha sido utilizada como material de construcción en numerosas presas tales como Niña Bonita, Maurín, La Coronela, Aguas Claras y otras (Armas et al. 1993). Las características físicas y mecánicas de la arcilla Capdevila han sido ampliamente estudiadas, aunque hay aspectos relativos al comportamiento tenso-deformacional no saturado de las presas de tierras, donde se relaciona la permeabilidad del suelo no saturado con la velocidad de consolidación, y donde juega un papel fundamental la curva de retención de agua en el comportamiento de los suelos no saturados, que se pretende analizar en este trabajo.

DESARROLLO

Para muchos problemas geotécnicos relacionados con los suelos no saturados, el conocimiento de las presiones de poros es de interés primordial. Estos valores son relativamente insensibles al coeficiente de permeabilidad saturada y a la función de la permeabilidad, pero a su vez resulta especialmente útil cuando se tiene en cuenta la dificultad que existe cuando se realiza la medición de los coeficientes de permeabilidad para un suelo no saturado.

La obtención de la función de permeabilidad se puede clasificar en: I) métodos directos, derivados a partir de la cantidad de agua que entra o sale del suelo debido a los cambios en la succión y II) métodos indirectos, que obtienen la función a partir del tamaño y distribución de los poros o de la curva de retención del suelo.

El coeficiente de permeabilidad para suelos no saturados no es constante sino que varía fundamentalmente con el contenido de humedad, o visto de otro modo, con el grado de saturación (S_r) o con la succión (S). Se han realizado estudios que relacionan el grado de saturación (S_r), definido como el volumen de agua entre el volumen total de poros, y la permeabilidad no saturada (K_unsat). Esta última se suele expresar como un porcentaje de la permeabilidad del mismo suelo en estado saturado (K_sat).

La curva de retención o curva característica para un suelo se define como la relación entre el contenido de agua o el grado de saturación del mismo y de la succión para el suelo (Alanís 2012), donde el contenido de agua se define como la relación porcentual entre el peso de la fase líquida y el peso de la fase sólida del suelo y la succión es la propiedad que tiene este para retener agua.

La curva de retención del suelo se puede utilizar para estimar varios parámetros empleados en la descripción de los suelos no saturados. Los estudios de laboratorio han demostrado que existe una relación entre la curva de retención y las propiedades del suelo no saturado (Fredlund y Rahardjo 1993), convirtiéndose en un procedimiento aceptable para predecir empíricamente la función de la permeabilidad de un suelo no saturado utilizando el coeficiente de permeabilidad del suelo saturado.

Dentro de los métodos para estimar la permeabilidad de suelos no saturadosse encuentran los que se explican en lo que sigue.

Método de Van Genuchten

En este método para determinar la permeabilidad de suelo no saturado se parte de determinar la curva de retención obteniendo el ajuste de la misma, ecuación (1), (Chae et al. 2010), (Krishnapillai and Ravichandran 2011), (Tejo et al. 2015).

donde: S_r es el grado de saturación, S es la succión total de la muestra, α y η representan los parámetros de ajuste del método. Conocida la curva de retención del suelo se puede obtener la permeabilidad no saturada del suelo en función de la succión que experimenta el suelo, m = 1 - 1 / η.

Conocida la curva de retención del suelo se puede obtener la permeabilidad no saturada del suelo k_unsat en función de la succión que experimenta el suelo, ecuaciones (2), (3) y (4).

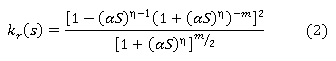
donde: k_unsat es la permeabilidad del suelo no saturado, K_r(S) es la permeabilidad residual planteada por Van Genuchten, S es la succión del intervalo analizado, k_sat es la permeabilidad saturada obtenida experimentalmente, α, m, η son los parámetros de ajuste del modelo.

Método de Fredlund

El método de Fredlund (Fredlund et al. 1994) para determinar la permeabilidad de suelo no saturado parte de conocer la permeabilidad saturada obtenida experimentalmente en el laboratorio, ecuaciones (5) y (6).

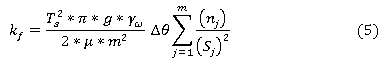
donde: T_s es la tensión superficial del agua, γ_ω es el peso específico del agua, g es la aceleración de la gravedad, μ_ω es la viscosidad absoluta del agua, Δθ es la variación del contenido volumétrico de agua, m y n son el número de intervalos, k_f es el coeficiente de permeabilidad planteado por Fredlund, k_sat es la permeabilidad saturada obtenida experimentalmente, p es la constante que cuenta para la interacción de poros de varios tamaños.

Partiendo de conocer la curva característica de un suelo se puede obtener la permeabilidad de los suelos no saturados empleando métodos empíricos y ensayos de laboratorios. Este tipo de enfoque es válido emplearlo para el estudio de las deformaciones en suelos a lo largo del tiempo.

El estudio del comportamiento volumétrico en los suelos parcialmente saturados ha sido objeto de investigaciones en las últimas décadas, debido a la influencia de la succión en su comportamiento. Los fenómenos más característicos del comportamiento del suelo en estado no saturado son los relacionados con las deformaciones volumétricas al modificar el grado de saturación. Los efectos del cambio de tensión total y los cambios de presiones de agua deben ser tratados de forma independiente para un suelo parcialmente saturado. Por lo tanto, (σ - u_a) se define como la tensión neta total, donde (u_a) es la presión de aire, σ es la tensión total, y (u_a - u_w) se define como la succión matricial del suelo, siendo (u_w) la presión de agua. El estado de tensión que se produce por la presión de agua se utiliza como la delimitación entre la mecánica de suelos saturados y no saturados.

El cambio de volumen global de una muestra de suelo debe ser igual a la suma de los cambios parciales de volumen de cada fase, cumpliéndose el principio de continuidad. Como las partículas sólidas y el agua son fundamentalmente incompresibles los cambios globales de volumen se deben a que el agua entra o sale de la muestra, para suelos saturados.

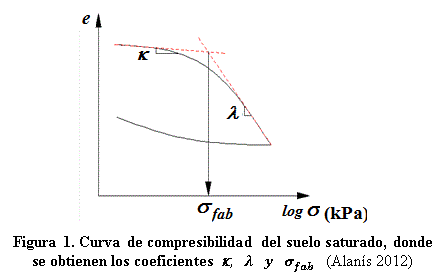
Con el empleo del modelo de Rojas y Alanís se puede predecir el comportamiento tenso-deformacional en suelos no saturados. El modelo parte de tomar en cuenta el comportamiento elástico y plástico del material no saturado, considerando en la formulación del modelo los factores κ y λ, los cuales serán tomados de la curva de compresibilidad del material saturado en su tramo virgen de carga y de descarga respectivamente (Rojas 2013), (Tristá et al. 2015).

Para el cálculo delos coeficientesê y ë correspondientescon su comportamiento elástico y plástico se utiliza la curva saturada (figura 1) empleándose las ecuaciones (7) y (8).

Cuando la muestra es compactada se tomará un esfuerzo de fabricación σ_fab el cual se añadirá para calcular los esfuerzos efectivos. Este esfuerzo de fabricación se obtiene de la curva de compresibilidad saturada trazando dos líneas rectas en los cambios de pendiente en la zona virgen como se puede apreciar en la figura 1. El esfuerzo de fabricación sería el esfuerzo de preconsolidación para el caso de muestras inalteradas.

La ecuación propuesta por Rojas y Alanís para determinar la relación de vacíos se muestra como ecuación (9), (Rojas 2013), (Tristá et al. 3015).

Comportamiento elástico

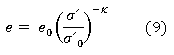
Comportamiento elastoplástico

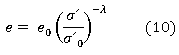
La formulación considera que:

donde: σ' son los esfuerzos efectivos, σ son los esfuerzos normales totales, hay que considerar el esfuerzo de fabricación antes mencionado en el valor final, (u_w) es la presión del agua, (u_a) es la presión de aire, (u_a - u_w) se define como la succión matricial del suelo, (χ) se considera que va a tener el mismo valor que el grado de saturación presente en las muestras.

Todos los materiales experimentan deformaciones cuando son sometidos a cambios en sus condiciones de esfuerzos. La deformación en los suelos no se produce de forma simultánea a la carga sino que se desarrolla en el transcurso del tiempo, evidenciándose que los suelos disminuyen su volumen conforme pasa el tiempo y aumentan las cargas por sedimentación sucesiva. El índice de consolidación para suelos saturados se puede obtener con el empleo de las ecuaciones (12) y (13) porque depende de la permeabilidad que tenga el suelo.

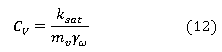
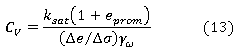
donde: C_v es el índice de consolidación, k_sat es la permeabilidad saturada, m_v es el coeficiente de compresibilidad, γ_ω es el peso específico de agua, Δe = e_i - e_f es la variación de relación de vacíos para variación de tensión Δσ, e_prom = (e_i + e_f)/2 (Crespo 2006).

El índice de consolidación influye en la obtención del tiempo, ecuación (14) o en el grado de consolidación del suelo saturado. El tiempo de consolidación para el caso de los suelos no saturados se obtiene por medio del empleo de la ecuación (15), que se consigue sustituyendo la ecuación (13) en la ecuación (14),tomando en consideración la permeabilidad no saturada y la curva de compresibilidad cuando varía la succión en el suelo.

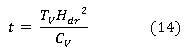
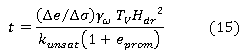
donde: C_v es el índice de consolidación, H_dr trayectoria de drenaje promedio más larga durante la consolidación: si drena en 2 sentidos H_dr = 1/2 H y si drena en un solo sentido H_dr = H (H es el espesor del estrato), T_v es el factor tiempo y depende del grado de consolidación U (%, K_unsat es la permeabilidad del suelo no saturado y está en función de la succión, γ_ω es el peso específico de agua, Δe = e_i - e_f es la variación de relación de vacíos para una variación de tensión Δσ en la curva de compresibilidad del suelo no saturado y e_prom = (e_i + e_f)/2 (Crespo 2006).

RESULTADOS DE LOS ENSAYOS DE LABORATORIO

Ensayos físicos y ensayo de compactación

Para la realización de los ensayos del suelo objeto de estudio y su clasificación se siguieron las orientaciones de las normas actualmente vigentes en cuanto a: determinación de la granulometría, peso específico, límite líquido, límite plástico e índice de plasticidad, Proctor estándar, permeabilidad saturada, consolidación y succión en los suelos. Los resultados de los ensayos físicos realizados a las muestras de suelos estudiadas se muestran en la tabla 1.

En función de los resultados obtenidos en la granulometría y límites de consistencia del suelo estudiado este clasifica como CH (arcilla de alta compresibilidad) (tabla 1).

Se realizó el ensayo de Proctor Estándar a las muestras de suelos de la formación Capdevila para obtener los valores de peso específico seco máximo y la humedad óptima y tener un parámetro de referencia a la hora de remoldear las muestras para la realización de los ensayos, ya que no se contaban con muestras inalteradas.

El método utilizado en esta investigación para la obtención de la permeabilidad saturada vertical fue el ensayo de carga variable (figura 2), empleando la norma vigente. Los resultados obtenidos de forma experimental se emplean en la obtención de la permeabilidad no saturada (K_unsat), empleando los métodos empíricos de Van Genuchten y Fredlund, para distintas succiones experimentadas por el suelo producto de la variación del grado de saturación del mismo.

Ensayo de consolidación

Para determinar la curva compresibilidad (evs σ) de suelo saturado, se tomó como base la norma vigente. A continuación se muestran las curvas de compresibilidad de los suelos estudiados para 100% de grado de saturación (figura 3).

De la curva de compresibilidad del suelo en condiciones saturadas se obtienen los valores de κ y λ con los que se trabaja en el modelo de Rojas y Alanís, que se emplea en la simulación de la curva de compresibilidad para distintos grados de saturación, para obtener la relación entre el tiempo de consolidación y la permeabilidad del suelo no saturado ya que la relación de vacíos en el suelo no saturados depende de la succión matricial (u_a - u_w).

Ensayo de Succión (Curva de retención)

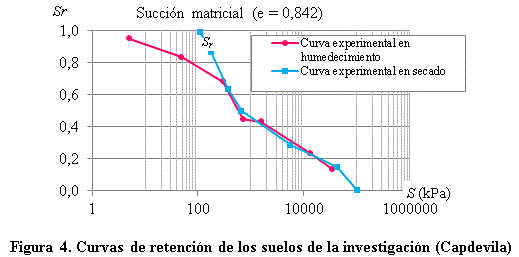
Para determinar la succión de los suelos, se tomó como base la norma correspondiente con la determinación de la succión en los suelos. Los resultados experimentales de la succiones de las muestras de suelo empleado en la investigación aparecen en la figura 4, representando la rama en secado y en humedecimiento.

SIMULACIÓN DE LAS CURVAS DE COMPRESIBILIDAD Y DE LA CURVA DE CONDUCTIVIDAD HIDRÁULICA

Curva de compresibilidad del suelo

Para el cálculo del tiempo de consolidación del suelo no saturado se obtiene la curva de compresibilidad del suelo de la formación Capdevila cuando varía la succión en el suelo producto de una variación del grado de saturación, empleando el modelo de Rojas y Alanís para los valores de k_carga= -0,0427, λ_carga= -0,3282 y k_descarga= 0,0396 de la curva de compresibilidad para 100% de grado de saturación. Los resultados obtenidos aparecen reflejados en la figura 5.

Curva de conductividad hidráulica

Método de Fredlund

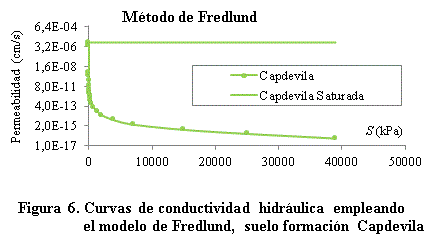
Empleando las ecuaciones (5) y (6) y los datos de la tabla 2, se determina la curva de conductividad hidráulica para el suelo de la formación Capdevila como se puede observar en la figura 6.

Método de Van Genuchten

Partiendo de conocer la curva retención de los suelos y realizado el ajuste de la misma con el modelo de Van Genuchten como se muestra en la figura 7 (a), se obtiene la curva de conductividad hidráulica para el suelo estudiado, figura 7 (b), empleando las ecuaciones (1) (4), se trabaja con la rama en secado de la curva de retención del suelo.

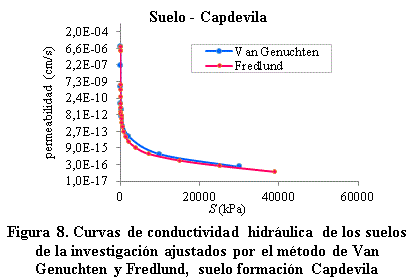
Ambos métodos son válidos para la obtención de la curva de conductividad hidráulica como se puede observar en la figura 8, para el caso del método de Van Genuchten la curva se obtiene a partir del ajuste de la curva de retención y para el caso de método de Fredlund se emplea la curva de retención obtenida experimentalmente sin realizar el ajuste.

CASO DE ESTUDIO

El comportamiento tenso-deformacional del suelo de una presa de tierra va a depender del grado de saturación producto de variaciones en la succión del suelo, provocando que la permeabilidad de la presa de tierra se vea afectada, así como el tiempo de consolidación del suelo.

Para el caso de estudio se analiza la variación del tiempo de consolidación para grados de consolidación entre 20 y 80%, cuando se producen cambios en la saturación del suelo de la presa de tierra (figura 9), que tiene una altura de 22m. En el análisis se toma en consideración los datos planteados en las tabla 3 y tabla 4, así como los resultados obtenidos en la simulación de las curvas de compresibilidad (figura 5) y de las curvas de conductividad hidráulica (figura 6, figura 7 y figura 8). Los resultados obtenidos para el suelo Capdevila se muestran en la figura 10 y figura 11.

Para la obtención de la variación de la tensión en el punto A de la presa empleada en el caso de estudio se empleó la ecuación (16). Siendo el peso específico seco máximo y la humedad óptima del suelo de la formación Capdevila obtenidos mediante el ensayo Proctor estándar (tabla 1).

En la figura 10 y figura 11 se evidencia que a medida que disminuye la permeabilidad del suelo producto de un aumento de la succión cuando varía la saturación del suelo se produce un aumento en el tiempo de consolidación, donde la influencia de la permeabilidad no saturada es más marcada cuando aumenta el grado de consolidación del suelo para la presa de tierra estudiada.

CONCLUSIONES

· La obtención de la permeabilidad de los suelos no saturados en el laboratorio resulta compleja si no se cuenta con el equipamiento adecuado, esta permeabilidad se puede determinar de forma análítica y de manera efectiva conociendo la curva de retención y la permeabilidad de los suelos para su condición saturada.

· Tanto para el método de Fredlund como para el de VanGenucthen se evidencia en la figura 6, figura 7 y figura 8 que un aumento de la succión trae consigo una disminución de la permeabilidad en los suelos, lo que valida la importancia de la succión en el comportamiento de los suelos no saturados.

· El tiempo de consolidación del suelo no saturado disminuye a medida que aumenta la succión en el suelo provocando una disminución en la permeabilidad del suelo no saturado. Siendo más marcada esta influencia a medida que aumenta el grado de consolidación del suelo.

 

 

REFERENCIAS BIBLIOGRÁFICAS

1. Alanís A. O. «Deformación volumétrica en suelos no saturados». Tesis de Maestría, Facultad de Ingeniería, Universidad Autónoma de Querétaro, Querétaro. México, extraído de: http://ri.uaq.mx/browse?type=dateissued, en mayo del 2013. (2012).

2. Armas R., Moreno L., Gandara W. y Morales P. «Presas de tierra homogéneas con arcilla Capdevila. Criterios de diseño». Ingeniería Estructural y Vial, (1993), vol. XIV, no. 3, pp. 85-92. ISSN: 0258-5952. La Habana. Cuba.

3. Chae J., Kim B., Park S. and Kato S. «Effect of suction on unconfined compressive strength in partly saturated soils». KSCE Journal of Civil Engineering, (2010), vol. 14, no. 3, pp 281-290. ISSN: 1976-3808. Publisher: Korea Society of Civil Engineering, Korea.

4. Crespo C. «Mecánica de suelos y cimentaciones». Limusa Noriega. 5ta edición. ISBN: 968-18-0069-9.México. (2006).

5. Fredlund D. and Rahardjo H. «Soil mechanics for unsaturated soils». University of Saskatchewan, John Wiley & Sons, Ed.: A Wiley-Interscience. ISBN: 978-0-471-85008-3. Saskatoon, Saskatchewan. Canadá. (1993).

6. Fredlund D., Xing A. and Huang S. «Equations for the soil-characteristic curve». Canadian Geotechnical Journal, (1994), vol. 31, no. 3, pp. 521-532. ISSN 1208-6010. Canadá .

7. Krishnapillai S. H. and Ravichandran N. «Improved soil-water characteristic curves and permeability functions for unsatured soils». 14^th Pan-American Conference on Soil Mechanics and Geotechnical Engineering. Toronto. Canadá. (Octubre 2011). (2011).

8. Rojas E. «La última pieza del rompecabezas: el comportamiento volumétrico de los suelos no saturados». Ciencia@UAQ, (2013), no. 2 pp. 1-16. Querétaro. México. extraído de:http://www.uaq.mx/investigación/revista_ciencia@uaq/ArchivosPDF/v6-n1/art8.pdf, en marzo del 2014.

9. Tejo J., González M. y Darby A. «Método numérico aplicados a ensayos de terreno para la determinación de la permeabilidad saturada». Obras y Proyectos, (2015), no. 7, pp. 45-51. ISSN: 0718-2813. Santiago de Chile. Chile. extraído de:http://www.scielo.cl/pdf/oyp/n17/art06.pdf, en noviembre del 2015.

10. Tristá J. G., Cobelo W., Quevedo G. y García C. «Comportamiento volumétrico de un suelo de la formación Capdevila en condiciones de saturación parcial». Revista Cubana de Ingeniería, (2015), vol. VI, no. 2, pp. 5-15. ISSN: 2223-1781, La Habana, Cuba.

 

 

Recibido: 10 de noviembre de 2015.
Aprobado: 7 de enero de 2016.

 

 

Jenny García Tristá, Willian Daniel Cobelo Cristiá, Gilberto Julio Quevedo Sotolongo. Facultad de Ingeniería Civil, Instituto Superior Politécnico José Antonio Echeverría (Cujae), La Habana. Cuba. Facultad de Ingeniería Civil, Instituto Superior Politécnico José Antonio Echeverría(Cujae), La Habana. Cuba. Facultad de Construcciones, Universidad Central «Marta Abreu» de Las Villas (UCLV), Santa Clara, Cuba. e-mail: [e-mail], e-mail: [e-mail], e-mail: [e-mail]