Introducción
La Dinámica de los Fluidos Computacional (CFD, por sus siglas en inglés), es considerada una rama de la mecánica de fluidos en la que se utilizan métodos numéricos y algoritmos para resolver y analizar problemas sobre el flujo de fluidos Versteeg and Malalasekera (1995); Ayremlouzadeh. and Ghafouri (2016); Cruz el al. (2000).
Las amplias y poderosas características de los programas desarrollados para estos fines permiten dar solución a prácticamente cualquier problema hidráulico. Sin embargo, suele requerir de mucho estudio y experiencia por parte del usuario; aún más en problemas con dos o más fluidos como es el caso de las conducciones libre (agua y aire).
El objetivo fundamental del presente trabajo es presentar recomendaciones para la simulación eficiente de obras en canales, dirigido a los usuarios con computadores personales de características corrientes. Para este fin se ha elegido la modelación en el software ANSYS Fluent, una obra de regulación: el vertedor de laberinto de un solo ciclo.
El vertedor de larga longitud de vertimiento de un solo ápice, llamado vertedor de pico de pato, Kraatz y Mahajan (1982), es muy usado ya que disminuye la repercusión de los cambios de caudales en la carga hidráulica sobre el vertedor al ser empleado como obra reguladora aguas arriba y por adaptarse eficientemente a la mayoría de situaciones debido a que admite apertura entre 45º y 70º según Kraatz y Mahajan (1982) y entre 50º y 84º según Tullis (Rojas y León, 2016). Este tipo de obra es de construcción y mantenimiento simples, y de funcionamiento seguro, figura 1.

Fig. 1 Vertedor de un solo ápice o pico de pato: a la izquierda con el ápice hacia aguas abajo y a la derecha con el ápice hacia aguas arriba
Para el caso particular de Cuba, se han presentado muy pocos trabajos con CFD, aunque la mayoría en problemas con regímenes de circulación libre. Es de destacar la profundidad y rigor científico de los trabajos realizados en el país, particularmente por el esfuerzo de contrastación de los modelos numéricos respecto a los ensayos de laboratorio con modelos físicos, o normas ISO.
En el año 2002 aparece en Cuba la primera investigación constatada que se desarrolla mediante un modelo CFD: “Modelación en conductos forzados utilizando el software ANSYS”, presentada por Márquez, R. y León, A. en el 2002. Posteriormente los trabajos de Alvin, M. y León, A. en el 2003; Herrera, U. y León, A. en el 2010, referenciados en Bosch et al. (2015) dan continuidad al primer trabajo.
La primera tesis de maestría en Ingeniería Hidráulica defendida en Cuba sobre la aplicación de modelos CFD a obras hidráulicas la presentó Patricia Bosch, (Bosch et al., 2015). Esta se centraba en el diseño hidráulico y estructural de obras hidráulicas.
En la Universidad Central “Marta Abreu” de Las Villas, Cuba, Gutiérrez, Y. y Suárez V. (2016) presentan un estudio de modelación con ANSY en vertedores de pared delgada validando los modelos con experimentos realizados en un laboratorio de la Hidráulica Universidad de San Carlos de Guatemala.
Los trabajos de tesis de grado por el título de Ingeniero Hidráulico presentadas en el “Instituto Superior Politécnico “José Antonio Echeverría” por Carriazo y León (2017) y Meluzzi y Rojas (2017), representan las investigaciones más cercanas en el tiempo realizadas en Cuba sobre el tema del presente trabajo.
A nivel de Latinoamérica, uno de los referentes más próximos, en cuanto a recomendaciones sobre estos modelos, está en un trabajo realizado en Colombia, Otálora (2016). En esta investigación se simulan varias obras: un vertedero triangular de pared delgada, un vertedor de laberinto asimétrico y un pico de pato; todos comparados con datos tomados de un modelo físico a escala reducida. Finalmente, el autor propone una guía metodológica para el modelado mediante ANSYS Fluent y hace recomendaciones de buenas prácticas.
A continuación, se describirán los pasos esenciales a seguir para desarrollar un modelo, comenzando por la construcción de la geometría del mismo. Al final del trabajo se realizan un grupo de recomendaciones básicas para comenzar la modelación de una obra.
Geometría
En una simulación, la definición primaria del fenómeno es la geometría. Esta debe en principio representar fielmente el volumen ocupado por los fluidos y las estructuras con las que interactúa.
Cuando se define la geometría se están condicionando también un número de elementos para determinada resolución de la malla, lo que a su vez influye directamente en la duración de la simulación. La eliminación de partes prescindibles en la geometría es una excelente manera de reducir el tiempo de cómputo sin afectar la calidad de los resultados.
En el caso particular de las obras en canales es importante determinar las longitudes de canal aguas abajo y aguas arriba respecto a la obra, tanto en los modelos matemáticos como en los modelos físicos a escala reducida.
En los modelos físicos la reducción del espacio es importante para la economía de la investigación y para ceder espacio del laboratorio a otros modelos. En el caso de los matemáticos, la reducción debe garantizar toda la influencia de la obra en el flujo sin aumentar el tiempo de cómputo innecesariamente. Las longitudes necesarias varían según la obra y el caudal simulado.
Si se cuenta con mediciones de nivel y velocidad, de un modelo físico a escala reducida o del propio prototipo, los puntos donde estas se realizaron, son una buena referencia para orientar la ubicación del inicio del tramo aguas arriba y el final del tramo aguas abajo respecto a los puntos de medición.
Hay que tener en cuenta que no todos los softwares CFD permiten declarar los niveles a la entrada y a la salida. Un modo de solventar esto es a través de la geometría, dividiendo la entrada o la salida en dos caras horizontales respecto al fondo del canal y fijándole a la inferior una altura igual al nivel del agua. Sin embargo, cuando se pretenden simular diferentes caudales, se vuelve tedioso y lento modificar la geometría y mallar para cada simulación, así que una buena alternativa es entrar agua en toda la cara y dar suficiente longitud al tramo aguas arriba para garantizar un patrón uniforme en las velocidades.
Cuando no se cuenta con datos reales y no se conoce del todo la magnitud de los fenómenos que provoca la obra en el flujo por el canal, es necesario, para determinar las longitudes de canal simulado, realizar simulaciones preliminares.
En el trabajo realizado, la estrategia seguida para minimizar el número de elementos del mallado se dirigió a la confección de soluciones, con mallas similares en diferentes geometrías, para determinar la repercusión y la viabilidad de la reducción de las dimensiones. El estudio de la geometría se realizó de forma paralela a la del mallado.
Las transformaciones respecto al modelo físico de laboratorio, están en la reducción del tramo aguas arriba y la eliminación de la parte superior, donde no circula agua. Además, se alargó el tramo aguas abajo para reproducir mejor la influencia de la obra. Estas modificaciones permitieron reducir la cantidad de elementos a la mitad respecto al modelo que reproducía las condiciones reales de laboratorio, sin influir en la simulación. La figura 2 muestra el mallado en la zona alrededor de la obra en contraste con lo que se observó y midió en el laboratorio.
En general las recomendaciones en la elaboración de geometrías para la simulación de vertimiento son:
La geometría debe tener una altura entre un 15% y un 25% por encima del mayor tirante de agua esperado para prevenir cualquier sobreelevación de la superficie.
Los tramos de canal deben reducirse al máximo sin interferir en el experimento, fijando como distancia mínima aguas arriba aquella donde comienza la influencia del vertedor sobre las líneas de corriente y siempre incluyendo los puntos donde se tengan mediciones, lo cual implica necesariamente un proceso de tanteo inicial modelo matemático-modelo físico.
Siguiendo las recomendaciones de Nengoue (2015), en obras simétricas, se puede usar una frontera simétrica por el eje del canal para reducir a la mitad la cantidad de elementos, pero esto impide comprobar que se reproduce simétricamente el flujo y el efecto de la obra.
Las recomendaciones anteriores pueden ser extrapoladas a otras obras.
Mallado
En una simulación, el mallado es la esencia de la aplicación del método de elementos finitos. Su calidad determinará la precisión en los resultados de la simulación, por lo que debe ser creada con la configuración idónea para cada problema. Para la generación de una malla adecuada deben considerarse, sobre todo, la geometría del problema (dimensiones; forma de las caras y bordes), las direcciones del flujo y los principales puntos de interés.
Las principales variables de optimización en el mallado son el tamaño de los elementos y su distribución. El tamaño del elemento debe cumplir un compromiso entre precisión y coste computacional. Cuantos más pequeños sean, más nodos y elementos. Esto implica, en principio, una mayor precisión, pero también un mayor tiempo de análisis (en función a la capacidad de cómputo), como se aprecia en la figura 3.
En el caso de la figura 3, se empleó una computadora personal con Windows 10-x64, procesador Intel(R) Core(TM) i5-7200U, CPU @ 2.50 GHz y Memoria RAM de 8 GB.
En la investigación se detectó que mallas con una distribución uniforme genera menor cantidad de elementos con respecto a otras con mayor exactitud en los resultados de la simulación (Tablas 1 y 2).
Tabla 1 Estadísticas de los mallados con diferentes distribuciones
| Distribución | |||
|---|---|---|---|
| Uniforme | Adaptativa | Proximidad y curvatura | |
| Cantidad de Nodos | 17 141 | 14 185 | 113 019 |
| Cantidad de Elementos | 85 925 | 70 555 | 632 112 |
| Tamaño medio de los elementos (mm) | 49 | 56 | 29 |
| Tiempo de cálculo aproximado en 100 iteraciones (min) | 2,5 | 2,0 | 25,0 |
En la tabla 2, la incoherencia entre el tiempo de cómputo y la exactitud en la medición de la función Proximity and Curvature se debe a que esta concentra un gran número de elementos con tamaños innecesariamente pequeños en regiones cercanas a los bordes, mientras estos son demasiado grandes en partes más alejadas, donde se generan los mayores errores.
Para obtener mayor control en el tamaño de los elementos se debe usar una distribución uniforme y elementos más pequeños en la zona donde ocurre la caída de agua en el vertedor (lo que permite reproducir con precisión el fenómeno), y la entrada si se está fijando un nivel para el que se requiere precisión.
Tabla 2 Errores para la profundidad (y) y la velocidad (v) entre el modelo CFD con las diferentes distribuciones y el modelo físico
| Distribución | ||||||
|---|---|---|---|---|---|---|
| Uniforme | Adaptativa | Proximidad y curvatura | ||||
|
|
aguas arriba | Laboratorio | 0,1816 | |||
| Simulación | 1,1844 | 0,1841 | 0,1866 | |||
| Error relativo (%) | 1,5678 | 1,3629 | 2,7324 | |||
| aguas abajo | Laboratorio | 0,1308 | ||||
| Simulación | 0,1321 | 0,1331 | 0,1363 | |||
| Error relativo (%) | 0,9763 | 1,7458 | 4,2031 | |||
|
|
aguas arriba | Laboratorio | 0,1891 | |||
| Simulación | 0,1915 | 0,1855 | 0,1807 | |||
| Error relativo (%) | 1,2663 | 1,9170 | 4,4594 | |||
| aguas abajo | Laboratorio | 0,2633 | ||||
| Simulación | 0,2729 | 0,2501 | 0,2861 | |||
| Error relativo (%) | 3,6455 | 5,0185 | 8,6436 | |||
Hay que tener en cuenta que la cantidad de elementos es muy sensible al cambio del tamaño para los tramos de canal, que representan la mayor parte. Esto está relacionado con la forma en que se acomodan los elementos para diferentes tamaños dentro de la geometría. Así un tamaño de 15 mm puede generar 1 millón de elementos y uno de 16,5 mm generar una malla de 400 mil elementos. Es importante además considerar que el tamaño de los elementos va a coincidir con el error absoluto máximo en los niveles de agua de la simulación si esta es buena. Esto se debe a que el método de cálculo determina los valores en cada nodo del elemento, pero los puntos intermedios se interpolan según el esquema de desratización empleado, lo que termina enclaustrando el nivel en un rango limitado por el propio tamaño del elemento:
Respecto a la forma de los elementos, lo más eficiente es emplear elementos hexaédricos que tienden a disminuir la cantidad sin afectar la solución del problema. Por otra parte, disminuye la falsa difusión en la interfaz aire-agua, al alinearse con la superficie del flujo. Además, la representación gráfica de la superficie de agua, como se observa en la figura 4, es más exacta.
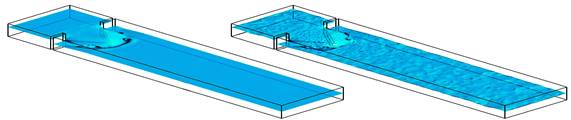
Fig. 4 Representación de la superficie del agua con un mallado de elementos hexaédricos (izquierda) y elementos tetraédricos (derecha)
Las recomendaciones para el mallado son:
Aplicar un tamaño máximo de elementos igual al error absoluto admisible para la simulación (esto se cumplirá si la simulación es buena). Con este principio se pueden estimar también el rango de los valores relativos.
Utilizar en la entrada y en la zona cercana al vertimiento al menos la mitad del tamaño en los elementos respecto a los tramos de canal para lograr mayor exactitud y definición.
Emplear elementos hexaédricos por alinearse con la superficie del agua.
Configuración de la simulación
Condiciones de frontera
Establecer condiciones de frontera significa asignar características de interacción a los límites del medio analizado. La existencia de estas condiciones de frontera, define el problema y la forma en la cual los sistemas computacionales determinan la convergencia.
Las condiciones de frontera utilizadas en CFD pueden dividirse en aquellas que permiten la entrada (Inlet) y la salida (Outlet) del fluido, las condiciones de presión y las limitaciones físicas (muros y estructuras rígidas). Las más comunes son: velocidad de entrada (velocity inlet), velocidad de salida (velocity outlet), flujo másico a la entrada (mass flow inlet), flujo másico a la salida (mass flow outlet), presión de entrada (pressure intlet), presión de salida (pressure outlet) y pared (Wall).
Las fronteras que interactúan libremente con el medio y las fronteras rígidas tienen concebido el tipo pressure outlet y wall respectivamente para su reproducción. Estos tipos de fronteras no son caso de estudio de la presente investigación.
Sin embargo, en conducciones libres las condiciones de entrada y salida deben ser tratadas con especial cuidado. Sucede que cuando se está simulando un canal se representa solo una porción de este y la existencia de flujo que circula (libre) por una porción de la altura del canal obliga a establecer una entrada y una salida a esa altura para evitar la alteración del modelo, o de lo contrario alargar los tramos de canal y con ello el número de elementos y la duración. La mejor opción en estos casos es emplear Open Channel Flow del modelo Multiphase y luego imponer niveles de entrada y de salida. Estos niveles deben ser seleccionados correctamente.
Modelo de turbulencia
Fluent cuenta con tres métodos en los que se basan los múltiples modelos aplicables: Reynolds Averaged Navier-Stokes Turbulence Models (RANS), Large Eddy Simulation (LES) y Direct Numerical Simulation (DANS). De estos se evaluó el RANS, que es el más ligero e inexacto de los métodos, pero también el más empleado, sobre todo en simulaciones ingenieriles por no requerir mallados demasiado finos. Su contraparte es el modelo DANS mucho más robusto y aplicable a investigaciones más rigurosas.
Del método RANS los modelos evaluados fueron el k-epsilon Standard y el Reynolds stress model.
El modelo k-epsilon define con robustez, economía, y exactitud razonable una gama amplia de flujos turbulentos y es el más comúnmente utilizado para problemas de este tipo (Launder and Spalding, 1974). Hay tres modelos k-epsilon elegibles: Standard: útil para la mayoría de problemas; RNG: más refinado en la simulación de remolinos en la turbulencia y flujos a altas velocidades; Realizable: contiene formulaciones alternativas.
Por otra parte, el Reynolds stress model (RSM) se presenta por los creadores de ANSYS Fluent como su mejor modelo de tipo RANS. Este modelo reproduce efectos aerodinámicos, remolinos, rotación, y cambios rápidos en la proporción de tensión de una manera más rigurosa. Tiene el potencial mayor para dar predicciones exactas en flujos complejos.
El modelo RSM según ANSYS® (2017) puede presentar problemas de inestabilidad y dificultad para converger. La solución que se ofrece es comenzar las iteraciones con un modelo k-epsilon para luego cambiarlo al modelo RSM. Recíprocamente, en los modelos k-epsilon cuando se obtengan residuales alejados de la convergencia sin tendencia a disminuir, recomienda cambiar y continuar con un modelo Reynolds Stress Model (RMS).
En general los dos modelos pueden ser considerados para la simulación de problemas de este tipo con buenos resultados como se muestra en la tabla 3.
Tabla 3 Comparación entre la velocidad (v) y la profundidad (y) entre el modelo CFD con el mallado propuesto y el modelo físico para los modelos de turbulencia k-epsilon y RMS
| Modelo k-epsilon | Cambio a modelo RSM | |||
|---|---|---|---|---|
|
|
aguas arriba | Laboratorio (m) | 0,1816 | |
| Simulación (m) | 0,1808 | 0,1821 | ||
| Error Relativo (%) | 0,4398 | 0,2945 | ||
| aguas abajo | Laboratorio (m) | 0,1308 | ||
| Simulación (m) | 0,1310 | 0,1351 | ||
| Error Relativo (%) | 0,1277 | 3,2564 | ||
|
|
aguas arriba | Laboratorio (m) | 0,1891 | |
| Simulación (m) | 0,1950 | 0,1842 | ||
| Error Relativo (%) | 3,1117 | 2,5760 | ||
| aguas abajo | Laboratorio (m) | 0,2633 | ||
| Simulación (m) | 0,2697 | 0,2645 | ||
| Error Relativo (%) | 2,4344 | 0,4593 | ||
La diferencia más notable entre los modelos está, en la representación gráfica del fenómeno. El RSM muestra la solución gráfica más detallada. Véase figura 5. Pero requiere más iteraciones para superar el salto en los residuales debido al cambio de modelo.
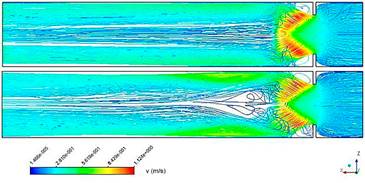
Fig. 5 Representación de las líneas de corriente mediante un modelo de turbulencia k-epsilon (figura superior) y el RSM (figura inferior)
Inicialización
La inicialización es un punto significativo en la configuración de la solución. Define los valores con los que se comienza el cálculo y puede tener repercusión en la solución final pues indica la dirección de los primeros cálculos. Para problemas de este tipo ANSYS ofrece dos métodos: el híbrido (Hybrid) y el estándar (Standard).
El método hibrido realiza interpolaciones a partir de condiciones de los valores en las condiciones de frontera para hallar buenos valores iniciales al problema. Por su parte el método Standard permite al usuario definir los valores iniciales (los valores por defecto corresponden a los adjudicados a las condiciones de frontera). El método estándar es más grotesco si no se proponen valores por el usuario. En general para la gran mayoría de problemas, ambos métodos son efectivos.
Especialmente para la simulación de canales abiertos se recomienda (para ambos métodos) realizar la inicialización a partir de la entrada (Inlet) mediante la opción Compute from. Además, cuando se usa un modelo multifase, se permite usar un método de inicialización Flat, que crea un volumen de agua inicial a partir del nivel de agua aportado en las condiciones de frontera para la entrada (si se usa como referencia para la inicialización).
Esquema de discretización del espacio
Los esquemas de discretización del espacio (Spatial Discretization Scheme) determinan los valores para cada variable en las caras del elemento en la dirección de flujo. ANSYS Fluent permite elegir entre varios esquemas según el tipo de problema de los cuales los más empleados para problemas de ingeniería por ser estables y simples son First-order upwind scheme y Second-order upwind scheme; esquemas que determinan los valores a partir de los valores aguas arriba del elemento (de primer y segundo orden respectivamente).
El esquema de primer orden determina el valor en la cara del elemento suponiendo que esta es igual al del centro del elemento inmediato aguas arriba. Este esquema es el que aparece por defecto en la mayoría de los problemas, sin embargo, no es el más preciso y crea falsa difusión. Su uso es recomendado por ANSYS Fluent para problemas con flujo laminar empleando mallados hexaédricos. En este caso específico la falsa difusión no será especialmente notable. Este es considerado el mejor esquema para comenzar el cálculo.
Por su parte el esquema de segundo orden utiliza el valor central y el gradiente de las 2 celdas aguas arriba del elemento para determinar el valor en una cara del elemento. Este esquema es de los más populares por brindar estabilidad y precisión. No obstante, en algunos casos puede no lograr buenas primeras aproximaciones.
ANSYS Fluent recomienda comenzar las simulaciones con un esquema de primer orden y luego de 100 iteraciones, cambiar a segundo orden. No obstante, para las simulaciones del vertedor pico de pato realizadas, esta estrategia no aportó resultados diferentes a comenzar con un esquema de segundo orden.
Control de la simulación
Distinto a la práctica común, la manipulación por el usuario en la simulación no debe finalizar cuando comienza la resolución del problema. Aún durante el cálculo es conveniente observar y orientar la solución para obtener la más exacta y con el menor número de iteraciones posibles. La preparación de la simulación es un proceso de prueba y error, en el que habitualmente se debe desestimar la solución y realizar correcciones. Para facilitar este proceso se recomienda salvar la solución cada un número determinado de iteración mediante la opción Autosave (every iterations). Las soluciones guardadas pueden ser luego cargadas para regresar a un punto estable en caso de divergencia. Existen varias estrategias para la reducción de tiempo y el refinamiento de la solución, algunas de las cuales fueron analizadas y serán evaluadas a continuación.
Factores de Relajación
Los factores de relajación (relaxation factor) controlan el cambio en la suposición del valor de una variable entre una iteración y la siguiente. Para un factor de relajación de 1 se aplica directamente el valor supuesto por el programa, para un valor inferior (underrelaxation) se aplica una reducción en la variación y para uno mayor (overrelaxation) se aplicaría un aumento en la fluctuación entre iteraciones.
La práctica más común es aplicar underrelaxation factors con el objetivo de disminuir la posibilidad de divergencias e incrementar la estabilidad en la solución, pero esto en teoría puede disminuir la velocidad con que converge. Mientras, los valores por encima, pueden ser usados para acelerar la convergencia, pero decrece la estabilidad en el cálculo. Estos valores además pueden influir indistintamente en la rapidez con que converge la solución pues al determinar el rango de búsqueda de un valor a partir de otro inicial, reducirlo o aumentarlo puede en determinados casos ser favorable y en otros desfavorable.
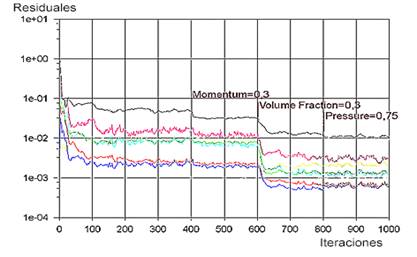
Con su aplicación durante el cálculo se experimentó y se comprobó el impacto en los gráficos de residuales. A continuación, se presenta el caso de cálculo en el que fueron aplicados underrelaxation factors para algunas variables de la manera que se refleja en la figura 6, partiendo de los valores por defecto, tabla 4. La estrategia en los casos estudiados fue intentar reducir el residual para la continuidad, habitualmente el más alto para problemas con la configuración empleada. Específicamente disminuir el factor de relajación por defecto a el cálculo de la presión resultó en este caso contraproducente, entonces se aplicó un factor superior.
Tabla 4 Factores de relajación por defecto
| Factor | Valor |
|---|---|
| Pressure (Presión) | 0,5 |
| Momentum | 0,5 |
| Volume fraction (Fracción de volumen) | 0,5 |
El refinamiento de la solución se produce porque al aplicarse underrelaxation factor se aminora el rango de búsqueda de la próxima solución y el programa determina con mayor rapidez la mejor solución de las posibles. Además, las soluciones se mueven en un menor rango por lo que las soluciones son muy estables: puede comprobarse la reducción en las fluctuaciones cuando se disminuyen los factores de relajación. La disminución de la variedad en las posibles soluciones también constituye una limitación porque pueden excluirse soluciones aún mejores.
Otro experimento aplicando todos los valores al mismo tiempo trajo resultados en el mismo orden para el gráfico de residuales, con menor número de iteraciones que para el caso en que fueron aplicados uno a uno tras la estabilización. Sin embargo, no se recomienda cuando se desconoce el impacto de cada underrelaxation factor pues puede que algún factor esté introduciendo resultados contraproducentes y sin que el usuario pueda ser consciente de esto. Además, los residuales pueden usualmente provocar saltos en la solución que, aunque se suelen disipar a medida que continúa el cálculo, pueden resultar demasiado grandes hasta el punto de ser detectados como divergencia por el programa. Por este motivo se recomienda guardar la solución antes de aplicar los cambios.
Lo más recomendable es usar los valores por defecto y modificarlos sólo si es necesario. Su uso se justifica en casos extremos de inestabilidad o de divergencia o como medida para refinar una solución que convergen o es estable. Se recomienda además ir modificando los valores tentativamente para comprobar los resultados. Disminuir demasiado los underrelaxation factor resulta contraproducente en algunos casos haciendo divergir la solución o creando inestabilidad luego de un número determinado de soluciones; cuando este es el caso debe emplearse por un breve número de iteraciones como último toque de refinamiento a la solución.
Criterios de convergencia
No se ha establecido un criterio de convergencia único aplicable a todos los problemas. Los gráficos de residuales pueden comportarse de manera muy diferente para problemas similares. Es necesario aplicar diferentes criterios de convergencia.
En todos los casos evaluar la convergencia de la representación y los valores obtenidos con la simulación, especialmente aquellos con mayor interés, es la medida que define finalmente si la solución es confiable o no. De no serlo es oportuno verificar primero la calidad del mallado.
Para la mayoría de los problemas, el criterio de la convergencia predefinido en ANSYS Fluent es suficiente. Este criterio requiere que los valores residuales globales a escala sean menores que 10-3 para todas las ecuaciones de continuidad, velocidad por cada eje, los diferentes volúmenes de fluidos (volume fraction) y las del modelo de turbulencia (para las ecuaciones de energía y de modelos de radiación en problemas que lo requieran el criterio es 10-6). Sin embargo, este criterio no es apropiado para todos los casos. Por ejemplo, en problemas en que los residuos fluctúan en un rango amplio de valores no debe considerarse convergente la solución basándose únicamente en el valor absoluto del residual, debe ser evaluado también su comportamiento. Es necesario asegurarse de que el residuo continúa disminuyendo o permanece bajo, para 50 o más iteraciones, antes de concluir que la solución ha convergido.
También es posible que los residuales fluctúan en pequeños valores alejados de los valores mínimos requeridos para la convergencia durante un gran número de iteraciones (habitual en modelos k-epsilon de turbulencia); puede considerarse un modelo estabilizado y la solución es aceptada como correcta aún sin converger. No obstante, a este tipo de resoluciones debe intentarse aplicar una estrategia de refinamiento con relaxation factors. En este caso también es conveniente controlar el cumplimiento de la continuidad empleando un monitor para el Mass Flow Rate pues es posibles que el gráfico de residuales se mantenga estable pero no se haya logrado estabilizar las diferencias entre la entrada y salida de agua en el modelo
Validación
Para la validación de los resultados de esta investigación se realizaron siete simulaciones con diferentes combinaciones de geometría y caudales aplicando las recomendaciones del presente trabajo. Ninguna corrida sobrepasó las 1500 iteraciones y un tiempo de 3 horas (aplicando los criterios de convergencia mencionados) en un ordenador, con Windows 10-x64, procesador Intel(R) Core(TM) i5-7200U, CPU @ 2.50 GHz y Memoria RAM de 8 GB.
La estrategia general para crear las mallas fue crear elementos de hasta 10 milímetros en los tramos de canal y de 5 milímetros en la entrada y en el vertedor. Por lo que se previó un error absoluto máximo en los niveles de 10mm.
Los resultados fueron comparados con los obtenidos en un modelo de laboratorio para la investigación publicada por Rojas, A. y León, A. (2016), donde se detallan las características del instrumental empleado.
La característica de las obras simuladas se relaciona a continuación enumeradas en correspondencia con la tabla 5 y la figura 7.
1. Caudal de 3,24 l/s por un vertedor con ángulo de apertura de 70º con contracción lateral y ápice en dirección aguas abajo
2. Caudal de 9,56 l/s por un vertedor con ángulo de apertura de 70º con contracción lateral y ápice en dirección aguas abajo
3. Caudal de 24,8 l/s por un vertedor con ángulo de apertura de 70º con contracción lateral y ápice en dirección aguas abajo
4. Caudal de 9,27 l/s por un vertedor con ángulo de apertura de 70º sin contracción lateral y ápice en dirección aguas abajo
5. Caudal de 24,21 l/s por un vertedor con ángulo de apertura de 70º sin contracción lateral y ápice en dirección aguas abajo
6. Caudal de 4,14 l/s por un vertedor con ángulo de apertura de 45º con contracción lateral y ápice en dirección aguas abajo
7. Caudal de 23,79 l/s por un vertedor con ángulo de apertura de 45º con contracción lateral y ápice en dirección aguas abajo
En la tabla 5 se muestra la comparación de los valores de velocidad y las profundidades aguas abajo y aguas arriba de la obra respectivamente obtenidos en el modelo físico de laboratorio y los errores relativos porcentuales.
En la tabla se observa que las diferencias en los niveles en laboratorio y en la simulación nunca es mayor a los 10 mm, fijados como tamaño de los elementos en los tramos de canal por lo que efectivamente se encuentran dentro de lo previsto. De todas las simulaciones la de mejores resultados resultó la número 3, donde ningún error relativo excedió el 1%. Por otro lado, en otras dos simulaciones encontramos errores relativos que exceden el 3%, es el caso del tirante aguas abajo para la simulación número 2 y la velocidad aguas abajo para la simulación número 7; esto se debe a que al tener menor magnitud son más sensible a este tipo de errores.
La figura 7 muestra la representación de las líneas de corriente, para cada uno de los modelos de validación con un modelo de turbulencia k-epsilon.
Tabla 5 Comparación entre la velocidad (v) y la profundidad (y) aguas abajo y aguas arriba de la simulación y el modelo físico de laboratorio
| Numeración que caracteriza la obra | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| aguas arriba | Laboratorio | 0,1233 | 0,140 | 0,1816 | 0,1992 | 0,2120 | 0,1367 | 0,178 | |
| Simulación | 0,1273 | 0,1433 | 0,1805 | 0,2036 | 0,2198 | 0,1392 | 0,1728 | ||
| Error relativo (%) | 3,24 | 2,36 | 0,61 | 2,21 | 3,68 | 1,83 | 2,92 | ||
| aguas abajo | Laboratorio | 0,0365 | 0,0948 | 0,1897 | 0,0646 | 0,1389 | 0,0421 | 0,1856 | |
| Simulación | 0,0363 | 0,0903 | 0,1895 | 0,063 | 0,137 | 0,0411 | 0,1916 | ||
| Error relativo (%) | 0,55 | 4,75 | 0,11 | 2,48 | 1,37 | 2,38 | 3,23 | ||
| aguas arriba | Laboratorio | 0,1129 | 0,1153 | 0,1308 | 0,1884 | 0,1911 | 0,1341 | 0,1366 | |
| Simulación | 0,1118 | 0,1138 | 0,1305 | 0,1885 | 0,1911 | 0,1336 | 0,1367 | ||
| Error relativo (%) | 0,97 | 1,30 | 0,23 | 0,05 | 0,00 | 0,37 | 0,07 | ||
| aguas abajo | Laboratorio | 0,0399 | 0,1152 | 0,2633 | 0,0683 | 0,176 | 0,0429 | 0,2419 | |
| Simulación | 0,0399 | 0,1125 | 0,2633 | 0,0705 | 0,169 | 0,0396 | 0,2437 | ||
| Error relativo (%) | 0,00 | 2,34 | 0,00 | 3,22 | 3,98 | 7,69 | 0,74 | ||
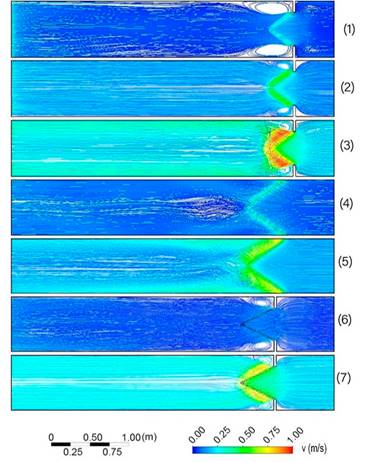
Fig. 7 Líneas de corriente para cada uno de los modelos de validación con un modelo de turbulencia k-epsilon y colores según la velocidad (v)
Las representaciones de las líneas de corriente son similares a la realidad coherentes en recorrido y velocidad con las condiciones del por la obra al flujo. Las líneas de corriente nos permiten percatarnos de la simetría en flujo, un buen indicio de calidad de la simulación.
Recomendaciones para comenzar una modelación
Generales:
1. Realizar simulaciones preliminares con mallados de menor resolución para que permitan prever los cambios en la geometría sin repercutir en el experimento y comprobar grosso modo los tirantes de agua estimados por el programa y los parámetros escogidos.
En la geometría:
2. Usar una altura de 3 a 5 veces el tamaño medio de elementos empleado en el mallado por encima del mayor tirante de agua esperado.
3. Emplear la menor longitud de canal posible sin excluir de la simulación los puntos donde se tengan mediciones y la influencia de la obra en la uniformidad de las líneas de corriente.
En el mallado:
4. Aplicar un tamaño máximo de elementos igual al error absoluto admisible para la simulación.
5. Utilizar en la cara de entrada y en la zona cercana al vertimiento, al menos la mitad del tamaño de los elementos que en el resto de la obra.
6. Emplear elementos hexaédricos.
De la configuración de la simulación:
7. Asignar niveles de entrada y de salida coherentes con las condiciones del experimento.
8. Comenzar las iteraciones con un modelo de tubulencia k-epsilon para luego cambiarlo al modelo RSM
9. Inicializar la solución con un método híbrido tipo Flat a partir de la cara de entrada.
10. Usar un esquema de desratización del espacio de primer orden para las primeras 100 iteraciones y luego cambiar para un esquema de segundo orden.
Del control de la simulación:
11. Salvar la solución cada 100 iteraciones mediante la opción Autosave
12. Ante pequeñas fluctuaciones en los valores de los residuales sin tendencia a la convergencia modificar los factores de relajación uno a uno y analizar la repercusión en los residuales y aplicar finalmente la mejor combinación posible para el problema.
Conclusiones
En el trabajo se profundiza sobre las simulaciones numéricas y se indaga en elementos, antes no tratados en Cuba y con escasa literatura en español: factores de relajación, esquemas de discretización, modelos de turbulencia.
Se lograron elaborar un grupo de recomendaciones a partir de las experiencias obtenidas con la simulación numérica (CFD) con modificaciones en el mallado, la geometría y la configuración de múltiples vertederos de laberinto de un solo ciclo y su calibración, respecto a los resultados obtenidos sobre modelos físicos a escala reducida. Estas recomendaciones son válidas para futuras simulaciones con el ANSYS Fluent, aplicables en la docencia y en investigaciones y en otros modelos CFD.
Se destaca en los resultados la importancia y la influencia de la intervención del usuario durante la simulación mediante cambios en los factores de relajación, la correcta interpretación de los gráficos de residuales y la aplicación de criterios de convergencia.