Instituto de Ciencias Básicas y Preclínicas "Victoria de Girón"

Centro de Investigaciones y Referencia de Aterosclerosis de La Habana. Policlínico "19 de Abril"

Árboles de regresión y otras opciones metodológicas aplicadas a la predicción del rendimiento académico

Dr.C. Jorge Bacallao Gallestey,1 Dr. José M. Parapar de la Riestra,2 Lic. Mercedes Roque Gil3 y Lic. Jorge Bacallao Guerra

Resumen

El presente trabajo se realizó con el fin de construir un algoritmo para detectar estudiantes con alto riesgo de fracaso académico e identificar los mejores predictores del rendimiento. Se caracterizaron los estudiantes que ingresaron en el primer año en el ICBP "Victoria de Girón" durante el curso 2001-2002 de acuerdo con su índice académico del preuniversitario, índice escalafonario, exámenes de ingreso, prueba de inteligencia y un indicador de su motivación profesional. Se emplearon árboles de clasificación para identificar los predictores relevantes y sus puntos de corte óptimos. Se utilizó un modelo de regresión ordinal para evaluar la importancia relativa de los predictores y proponer el algoritmo de predicción. A partir del índice escalafonario, exclusivamente, se obtuvo un procedimiento de clasificación, que permitió identificar a los estudiantes de mayor riesgo de fracaso académico. Los puntos de corte fueron 87 y 91 puntos, que definen una tricotomía para el pronóstico del rendimiento.

Palabras clave: Arboles de clasificación, regresión ordinal, predicción del rendimiento, admisión en la enseñanza médica superior.

Desde la década de los 90 se aplica en el Instituto de Ciencias Básicas y Preclínicas "Victoria de Girón" un sistema semiautomatizado para el pronóstico del rendimiento académico. A partir de las bases de datos de los estudiantes de nuevo ingreso y mediante la aplicación de modelos estadísticos de predicción, se obtiene un índice individual que mide la probabilidad de fracaso académico, el que se utiliza para caracterizar a cada uno de los estudiantes y para aplicar medidas preventivas con los que rebasan cierto umbral de riesgo.

Para estimar la probabilidad de éxito, se han utilizado diversos modelos analíticos de predicción que difieren en su estructura, en sus supuestos estadísticos y en su grado de complejidad. Estos modelos predictivos (Bacallao J, Antón M. Aspectos metodológicos relativos a la predicción del rendimiento académico en los centros de enseñanza médica superior. Trabajo presentado a concurso para el mejor trabajo científico del MINSAP en el área de investigaciones aplicadas; 1992) se han empleado con varios fines: la predicción individual del riesgo,1,2 el pronóstico de la promoción global en un curso académico3 y la identificación de predictores relevantes.4 También se han empleado diversos recursos analíticos de naturaleza estadística para la validación de los propios modelos de predicción.5,6

Las variables que se emplean para el pronóstico se eligen dentro de una batería que históricamente ha incluido: el índice académico del preuniversitario, una prueba de ortografía, pruebas de nivel de entrada, exámenes de ingreso y variantes de diversas pruebas psicométricas. En la actualidad, la predicción se lleva a cabo mediante la aplicación de diversos modelos predictivos o de una heurística simple, a partir del índice académico del preuniversitario (IAP), los exámenes de ingreso (MAT, BIOL, HIST), el resultado de una prueba de inteligencia general (INTEL) y un indicador de motivación profesional (MOTIV). INTEL se expresa en una escala ordinal creciente de 7 niveles y MOTIV en una ordinal decreciente de 5 niveles.

Otras facultades de Medicina del país han aplicado también diversos modelos estadísticos multidimensionales para predecir el rendimiento y para identificar predictores relevantes.7,8

La dirección del proceso de admisión, usualmente responsabilidad del personal de la Secretaría Docente de las facultades, requiere que este proceso pueda llevarse a cabo en poco tiempo -1 ó 2 semanas a lo sumo- mediante la aplicación de algoritmos simples y fáciles de interpretar.

En un trabajo previo se ha argumentado que los procesos de admisión deben regirse por estrictas consideraciones de costo-beneficio, lo cual implica definir con precisión los objetivos que se persiguen y, en función de dichos objetivos, simplificar al máximo el proceso. La mayor simplificación posible del proceso supondría el empleo del menor número posible de indicadores y la conversión de éstos en variables binarias u ordinales a partir de la definición de puntos de corte apropiados. El mismo argumento es válido para la identificación de estudiantes en riesgo.

Si fuera posible hacerse con una variable única, toda la evidencia previa indica que el mejor candidato es el índice académico del preuniversitario (IAP) o el índice escalafonario, que integra IAP y los exámenes de ingreso.1,2,5-8 Si esta simplificación se obtuviera sin un sacrificio importante de capacidad predictiva, se dispondría de un instrumento idóneo para mejorar los indicadores de aprovechamiento del proceso de enseñanza-aprendizaje, porque se podría actuar oportunamente sobre los estudiantes en riesgo.

El presente trabajo tiene el propósito de encontrar los predictores más relevantes y sus cortes óptimos para predecir el riesgo individual de los estudiantes de nuevo ingreso en la carrera de Medicina, construir un algoritmo sencillo de identificación de estudiantes en riesgo y poner a prueba la hipótesis de que el índice escalafonario es suficiente para la contrucción de este algoritmo.

Métodos

El universo del estudio se restringió a los nuevos ingresos en la carrera de Medicina durante el curso 2001 - 2002 con expedientes completos (n=152 estudiantes). Esta decisión excluye a los estudiantes que ingresan por vías que no exigen pruebas de ingreso o historia académica del preuniversitario, y a los que no fueron sometidos a las pruebas que hace de rigor, la unidad de orientación estudiantil de la institución.

Se consideraron completos los expedientes que contenían las variables siguientes: índice académico del preuniversitario, índice escalafonario, resultados de los exámenes de ingreso en Matemática, Biología e Historia, resultados del test de inteligencia aplicado, un indicador de motivación y los resultados del rendimiento, expresados como promedio de todas las asignaturas.
El indicador de motivación consiste en una variable ordinal expresada en una escala de 1 a 5, que se obtiene a partir de varias pruebas conocidas de actitud y personalidad.

El promedio de todas las asignaturas se convirtió a una variable dicotómica que toma el valor 1 ("fracaso") si el promedio es inferior a 3,75 y el valor 2 ("éxito") en caso contrario. Esta conversión convencional -exigente para el éxito- tiene la intención de que el algoritmo de selección resultante tenga una sensibilidad alta para detectar el riesgo académico.

Para los efectos de validación del algoritmo resultante de este estudio, se incluyó también un indicador pronóstico ("progno", indicador ordinal con 4 categorías: excelente, bien, tránsito y riesgo; que emite de rutina la secretaría docente de la institución, basándose en una heurística simple), obtenido a discreción a partir de una apreciación global subjetiva de todos los indicadores de entrada.

Los procedimientos analíticos empleados fueron los siguientes:

• Árbol de clasificación que permite asignar los sujetos a grupos de riesgo, identificar los predictores relevantes, y ubicar sus puntos de corte óptimos.
  
• Modelos de "regresión ordinal" para evaluar la importancia relativa del predictor elegido y seleccionar una métrica óptima para la operacionalización de dichos predictores.

El ajuste de un árbol de regresión se llevó a cabo con el programa SYSTAT versión 9.0, se tomó como variable de respuesta, la condición de "éxito" o "fracaso" y como predictores, el índice escalafonario, los exámenes de ingreso (MAT, BIOL e HIST), la prueba de inteligencia (TESTINTEL) y el indicador de motivación profesional (MOTIV).

La regresión ordinal se realizó con el paquete SPSS versión 11.5, tomando como variable dependiente el promedio de las calificaciones en las asignaturas del primer año de la carrera de Medicina.

I . Sobre los árboles de clasificación

Los árboles de clasificación se emplean para asignar sujetos a las clases de una variable dependiente a partir de sus mediciones en uno o más predictores. Modernamente, los árboles de clasificación (AC) constituyen uno de los recursos instrumentales básicos de la llamada "minería de datos".Producen cortaduras en los regresores para predecir o explicar variables dependientes discretas (usualmente binarias) y constituyen, por la interpretación inmediata de sus resultados y por su condición "no paramétrica", una opción favorable entre otras alternativas como el análisis discriminante, el análisis de clusters o la regresión logística binaria o politómica.

Los AC son jerarquías de cortes que se construyen a partir de los predictores, de modo que se maximice cierto criterio de asociación con la variable de respuesta. Cada cortadura da lugar a una partición de los sujetos en 2 grupos: avanzando en pasos sucesivos a lo largo del árbol jerárquico de cortaduras se llega a la clasificación final.9

El uso de los árboles de clasificación no es frecuente en el ámbito de las probabilidades o del reconocimiento de patrones, pero se han extendido considerablemente en el ámbito del diagnóstico, las ciencias de la computación, la taxonomía y la teoría de la decisión. Los árboles tienen una expresión gráfica que facilita su intepretación.

Una diferencia importante entre los árboles de clasificación y otras técnicas con propósitos afines como el análisis discriminante, es que en estas últimas, las decisiones de asignación de los sujetos a un grupo son simultáneas; mientras que en los primeros, es jerárquica y recursiva.10

Los AC son más flexibles que otras técnicas de clasificación porque permiten incorporar predictores medidos virtualmente en cualquier escala: continua, ordinal o mezclas de ambas escalas. Cualquier transformación monótona en la escala de medición que preserve el orden en las categorías de una variable ordinal, preserva también la clasificación que se obtiene si se emplea un AC.

La capacidad discriminatoria que se gana al añadir una nueva cortadura al criterio de clasificación, puede medirse u observarse directamente, en lugar de tener que estimarse como en el análisis discriminante o en otros modelos predictivos.11

Es posible utilizar combinaciones lineales de cortaduras, del mismo modo que en el análisis discriminante (AD) se utilizan combinaciones lineales de predictores. No obstante, hay una diferencia crucial: mientras que en el AD, el número de combinaciones lineales está acotado superiormente por el número de predictores menos 1, en los AC puede realizarse un número ilimitado de cortaduras, lo cual permite aprovechar mucho mejor la información contenida en los predictores. Por ejemplo, un mismo predictor podría arrojar varias cortaduras para mejorar su capacidad predictiva, algo que es imposible en el análisis discriminante o en cualquier otro modelo estadístico que suponga una relación monótona de los predictores con la variable dependiente.

En general, se usan 2 algoritmos para la construcción de los AC. El primero de ellos, conocido como QUEST (quick unbiased efficient statistical tree)12 es rápido e insesgado en la identificación de los predictores relevantes, algo especialmente importante en el caso de predictores ordinales con muchos niveles, en los que las cortaduras recursivas tienden a producir sobreajuste (overfitting) y por tanto, a seleccionar demasiados predictores (Quinlan JR, Cameron-Jones RM. Oversearching and layered search in empirical learning. Proceedings of the 14th International Joint Conference on Artificial Intelligence. Vol 2. Montreal.: Morgan Kaufman p.1019-24). El otro algoritmo es el CART (classification and regression trees) que lleva a cabo una búsqueda exhaustiva de todas las posibles cortaduras para minimizar el porcentaje de clasificación incorrecta.

II. Sobre la regresión ordinal

La regresión ordinal (RO) permite asignar una métrica óptima a los regresores discretos de un modelo de regresión múltiple. Se trata, en síntesis, de elegir la recodificación de los predictores de acuerdo con una métrica ordinal tal, que se optimice el ajuste del modelo. De este modo, se extrae de cada regresor su mayor capacidad predictiva posible mediante una recodificación óptima de sus valores posibles en una nueva escala de naturaleza ordinal.

Resultados

En el árbol de regresión, cuando al modelo (que tiene 2 salidas, "éxito" y "fracaso") se hacen ingresar todos los predictores (índice escalafonario, Matemática, Biología, Historia, motivación y test de inteligencia), sólo elige como entrada el índice escalafonario (en 2 ocasiones sucesivas) y selecciona como puntos de corte, los valores que muestra la figura: alrededor de 87 y 91 puntos. De esta forma quedó definida una variable politómica con 3 niveles (escalaf) como muestra la figura 1.

FIG. 1. Resultados del ajuste de un árbol de clasificación.

Como es fácil constatar, el árbol de clasificación define un algoritmo con 3 nodos terminales que arrojan una clasificación en 3 categorías, a partir de 2 cortaduras sólo en el índice escalafonario:

• Grupo 1: indesc<87
  
• Grupo 2: 87= indesc<91
  
• Grupo 3: indesc = 91

Con la media aritmética de las calificaciones, estratificadas de acuerdo con los valores de progno y escalaf se intenta mostrar que con sólo 1 predictor (el índice escalafonario), y mediante un criterio de clasificación muy sencillo, es posible construir una tipología adecuada para la clasificación de estudiantes en riesgo (tabla 1).

TABLA 1. Rendimiento académico promedio de acuerdo con 2 predictores ordinales del rendimiento.

Escalaf
Progno	1	2	3	Total
1	3,38	3,48	4,53	3,54
2	3,54	3,72	4,39	3,90
3	3,37	4,00	4,42	4,21

Debe notarse que:

• El predictor que se obtuvo a partir de las cortaduras óptimas derivadas del árbol de clasificación (escalaf) tuvo una relación monótona con el rendimiento académico de los estudiantes. Basta ubicarse en cualquier fila de la tabla y observar cómo crecieron las calificaciones al pasar de un nivel a otro de escalaf.
  
• Los resultados de las calificaciones también fueron crecientes de acuerdo con progno, pero no lo fueron para todas las categorías de escalaf (no en todas las columnas se mantuvo la tendencia creciente).

En el rendimiento académico se mantuvo la misma estructura que en el cuadro anterior, pero las calificaciones se estratificaron de acuerdo con escalaf y un indicador de la motivación profesional (motiv) (tabla 2).

TABLA 2. Rendimiento académico promedio de acuerdo con 2 predictores ordinales del
rendimiento.

Escalaf
Motiv	1	2	3	TOTAL
1	-	3,00	-	3,00
2	3,47	4,00	4,57	4,19
3	3,47	3,75	4,54	4,09
4	3,37	3,88	4,51	3,98
5	--	3,00	--	3,00
Total	3,46	3,76	4,50	4,05

Pudo comprobarse que:

• Escalaf conservó su monotonicidad para cada nivel del indicador de motivación (motiv), es decir, para 1 de las filas.
  
• El recíproco no se cumplió.
  
• Los peores rendimientos ocurrieron en los estudiantes muy motivados (motiv=1) o nada motivados (motiv=5).
  
• Si el pronóstico basado en el índice escalafonario fue bueno, fue indiferente tener mucha o poca motivación.
  
• Si el pronóstico basado en el índice escalafonario fue malo, también fue indiferente la motivación.

La comparación de 3 de los predictores del rendimiento (escalaf, progno y tesintel) de acuerdo con 3 importantes criterios de comparación: correlación simple del predictor con la calificación final; correlación parcial (asociación remanente después de remover el efecto de los otros predictores) y la importancia relativa (efecto directo, después de eliminar el efecto intermedio de los otros predictores, equivalente al "coeficiente de camino" análisis en que la variable se toma como predictora del rendimiento académico y las 2 restantes, como mediadoras) se muestra en la tabla 3.

TABLA 3. Correlaciones simples, parciales e importancia de 3 predictores en relación con el
rendimiento académico en el primer año de Medicina.

Correlaciones
Predictores	Simple	Parcial	Importancia
escalaf	.437	.366	.839
progno	.268	.021	.031
tesintel	.230	.114	.131

Pudo observarse que:

• La correlación simple de escalaf con el rendimiento fue casi el doble que la del pronóstico a discreción y la de la prueba de inteligencia.
  
• La correlación parcial fue aún mayor relativamente. Casi toda la capacidad predictiva de progno ocurrió a expensas del índice escalafonario, al punto de que si se remueve su efecto, la capacidad predictiva remanente es despreciable.
  
• Aunque la prueba de inteligencia fue relativamente independiente en su capacidad predictiva, es probablemente mucho más inespecífica y por eso su correlación parcial sigue siendo más de 3 veces menor.
  
• Por último, la importancia relativa mostró que el índice escalafonario fue casi 27 veces más importante que el pronóstico a discreción y casi 6 veces y media más importante que la prueba de inteligencia.

En el reescalamiento óptimo de las variables escalaf, progno y tesintel, a partir de un modelo de regresión con variables ordinales, se observó la capacidad discriminatoria de las 3 categorías de escalaf y la poca capacidad discriminatoria de tesintel, 3 de cuyas categorías se superponen. Hay prácticamente sólo 2 niveles de discriminación en progno y tesintel, lo que muestra la insuficiente validez de dichas variables (figs. 2, 3 y 4).

FIG. 2. Reescalamiento óptimo del predictor escalaf.

De la figura anterior se interpreta que si se practica una regresión del rendimiento sobre la variable escalaf (variable ordinal con 3 niveles), el modo óptimo de redefinir los valores de dicha variable para obtener el mejor ajuste posible consiste en asignarle los valores aproximados de -1,2; -0,5 y 1,0 respectivamente. Es fácil constatar visualmente, que existió una clara diferencia entre los diferentes niveles de escalaf.

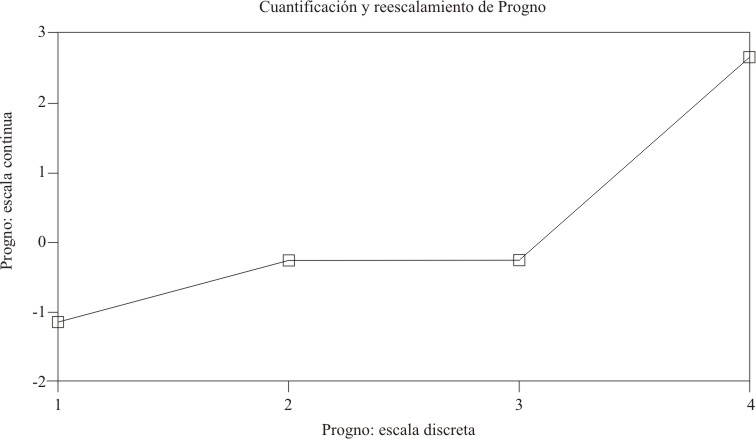
FIG. 3. Reescalamiento óptimo del predictor progno.

A diferencia de lo que se observó con escalaf, prácticamente no hubo discriminación entre las categorías 2 y 3 de progno, que corresponden aproximadamente al valor 0 en la métrica ordinal transformada, y hubo poca discriminación entre estas 2 categorías y la categoría inferior 1, que corresponde al valor de cero en la nueva métrica. Sólo el valor 4 (aproximadamente 2,5 en la nueva escala ordinal) se diferenció claramente del resto.

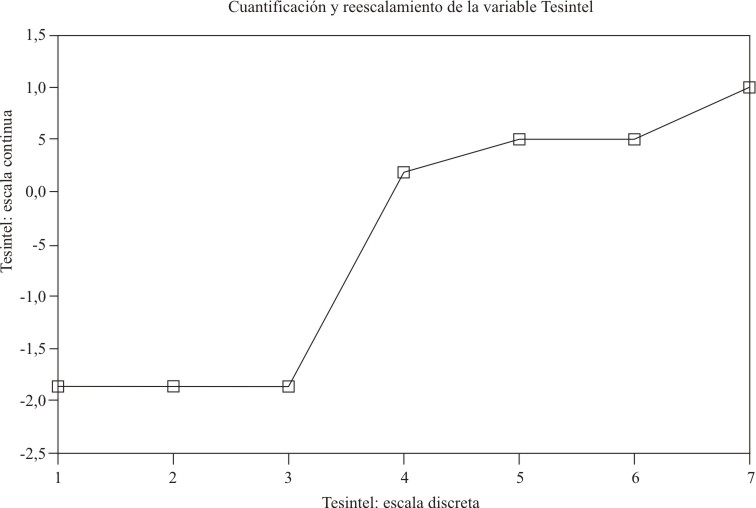
FIG. 4. Reescalamiento óptimo del predictor tesintel.

En relación con el test de inteligencia (tesintel) hay 2 grupos de valores: los correspondientes al 1, 2 y 3 de la escala original y los que corresponden al 4, 5, 6 y 7. Ello indica que tesintel podría tener mejores propiedades discriminatorias con respecto al rendimiento académico si se codifica en una dicotomía mediante la agrupación ya señalada de sus valores originales.

Discusión

Se concluyó que con sólo el índice escalafonario es posible construir un simple algoritmo predictivo del rendimiento académico, lo cual confirmó la hipótesis formulada. El algoritmo se basa en construir una tricotomía sobre el recorrido del índice escalafonario, utilizando 2 puntos de corte óptimos para el pronóstico, que se ubican alrededor de 87 y 91 puntos.El índice escalafonario convertido en variable ordinal fue superior a otros predictores del rendimiento y mostró mayor capacidad discriminatoria.

La capacidad predictiva podría mejorarse,1-8 pero sólo a expensas de complicar el modelo.

Summary

This paper is aimed at constructing an algorithm to detect students at high risk for academic failure and at identifying the best preformance predictors. The students that were admitted in the first year at Victoria de Girón Institute of Preclinical Basic Sciences during the course 2001-2002 were characterized according to their preuniversity academic index, roster index, admission test, intelligence test and an indicator of their professional motivation. Classification trees were used to identify the relevant predictors and their optimal cut-off points. A model of ordinal regression was used to evaluate the relative importance of the predictors and to propose the prediction algorithm.Starting only from the roster index, it was obtained a classification procedure that allowed to identify students at the highest risk for academic failure. The cut-offs were 87 and 91 points, which define a trichotomy for the performance prognosis.
.
Key words: Classification trees, ordinal regression, performance prediction, admission at higher medical education

Referencias bibliográficas

1. Bacallao J, Valenti J, Rodríguez E, Romillo MD. Pronóstico del rendimiento académico mediante un enfoque bayesiano no paramétrico. Educ Med Sup 1991;5:29-37.
   
2. Bacallao J, Aneiros R, Rodríguez E, Romillo MD. Pronóstico y evaluación del rendimiento en un ensayo pedagógico controlado. Ed Med Sup 1992;6: 91-9.
   
3. Antón M, Bacallao J, Valenti J, Casado A. Modelo markoviano para un pronóstico global del rendimiento académico. Educ Med Sup 1993;7: 51-5.
   
4. Bacallao J. Al rescate de las pruebas de nivel de entrada como predictores del rendimiento en la enseñanza médica superior. Educ Med Sup 1996;10:12-8.
   
5. Bacallao J, Antón M, Rodríguez E. La validación del pronóstico del rendimiento en un centro de enseñanza médica superior. Educ Med Sup 1991;5:75-82.
   
6. Bacallao J. Las curvas ROC y las medidas de detectabilidad para la validación de predictores del rendimiento docente. Educ Med Sup, 1996;10:3-11.
   
7. Rodríguez R, Bacallao J, Díaz PA, Morejón M. Valor predictivo de algunos criterios de selección para el ingreso a la carrera de Medicina. Educ Med Sup 2000;14:17-25.
   
8. Rodríguez R, Díaz PA, Moreno M, Bacallao J. Capacidad predictiva de varios indicadores de selección para el ingreso a la carrera de Medicina. Educ Med Sup 2002;14:128-35.
   
9. Ripley BD. Pattern recognition and neural networks. Cambridge: University Press; 1996.
   
10. Breiman L, Friedman JH, Olshen RA, Stone CJ. Classification and regression trees. Monterrey CA: Wadsworth & Brooks / Cole Advanced Books and Software; 1984.
11. Lim TS, Loh WH, Shih YS. An empirical comparison of decision trees and other classification methods. (Technical Report 979. Departments of Statistics). Madison: University of Wisconsin; 1997.
    
12. Loh WY, Shih YS. Split selection methods for classification trees. Statistica Sinica 1997; 7: 815-840.

Recibido: 15 de marzo de 2004. Aprobado: 5 de abril de 2004.
Dr.C. Jorge Bacallao Gallestey. Instituto de Ciencias Básicas y Preclínicas "Victoria de Girón". Ave. 146 No. 3102. Playa, Ciudad de La Habana, Cuba . CP 11600.

1Doctor en Ciencias de la Salud. Profesor Titular.
2Profesor Auxiliar.
3Licenciada en Psicología.
4Licenciado en Matemática.