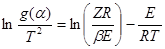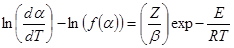Introducción
En los últimos años, han sido extensamente discutidas las potencialidades de la biomasa como fuente renovable de energía.1-5 Los residuos madereros, entre la amplia diversidad de biomasas, ocupan un lugar importante, por sus grandes volúmenes existentes y el impacto ambiental y económico que reviste su utilización.3
Este trabajo centra la atención en los residuos madereros (aserrín), de Teca y Guachapelí, árboles cultivados en la República de Ecuador. El primero, un árbol fino, noble y de rápido crecimiento, cuyas características lo convierten en una de las maderas duras más apetecidas del mundo, debido a su color y larga durabilidad. El segundo, un árbol de rápido crecimiento, forma variada, produce un fuste corto que se bifurca desde poca altura, moderadamente dura, durable y resistente al ataque del comején.6
La madera está compuesta fundamentalmente de tres componentes básicos estructurales, hemicelulosa, celulosa y lignina. Por lo general las especies maderables son más ricas en lignina que las herbáceas. Usualmente contienen de celulosa (40-50% m/m), hemicelulosa (20-40%m/m) y lignina (10-40% m/m).
La pirólisis es una ruta prometedora para la obtención de productos sólidos (carbón), líquidos (alquitrán) y gaseosos (volátiles), como fuentes alternativas de energía.7-11 Los parámetros de este proceso tales como: temperatura, tiempo de residencia, velocidad de calentamiento y tamaño de partícula, pueden afectar la calidad y cantidad del carbón vegetal obtenido y su interacción con el ambiente. De estos parámetros, la temperatura ha sido el más estudiado y se ha demostrado que tienegran influencia en la producción del carbón.12-13 El efecto de la velocidad de calentamiento y la temperatura de pirólisis, en los rendimientos en masa del biochar, ocasionan una disminución en el rendimiento del mismo, con el aumento de ambos parámetros. Esto se atribuye a la significativa descomposición primaria de la biomasa a temperatura más alta o a la descomposición secundaria del carbón. En consecuencia, para una alta producción de biochar debe seleccionarse una baja temperatura y una baja velocidad de calentamiento.14
El estudio cinético de la pirólisis de la biomasa es relevante, ya que constituye el paso inicial de la combustión y la gasificación, además que aporta información para el diseño y operación eficiente de reactores. Algunos autores manifiestan que, el uso de diferentes velocidades de calentamiento durante la pirólisis de la biomasa, tiene un mínimo impacto en el factor de frecuencia, otros indican que las reacciones de conversión de biomasa, son cinéticamente más lentas a mayor tasa de calentamiento.15-17
La influencia de la velocidad de calentamiento (() en los valores de energía de activación y factor pre-exponencial, fue estudiado por Soria y colaboradores y demostraron que ambos parámetros cinéticos aumentan cuando aumenta la (. Los autores refieren que existe un error de alrededor de 40% cuando se determinan dichos parámetros a bajas velocidades de calentamientos (15, 25K/min) y se extrapolan los datos a altas ( (150, 200 K/min).18 Sin embargo, poco ha sido dicho de la influencia de la velocidad de calentamiento en el modelo cinético, cuando se estudian procesos de pirólisis de biomasas.
Este proceso es complejo, debido a las diferentes reactividades y estabilidad térmica de los constituyentes de la biomasa. Dependiendo de las condiciones de operación, ocurren diversas reacciones asociadas con la descomposición térmica de cada componente, que a su vez producen cambios en las propiedades del material 6,19-20 Stefanidis y colaboradores sugirieron que el craqueo pirolítico de biomasa es un mecanismo de reacción en red extremadamente complejo, el estudio químico de este proceso puede ser simplificado estudiando la pirólisis de celulosa, hemicelulosa y ligninapor separado.21) Quesada y colaboradores han utilizado una idea similar, para el estudio de la cinética de la pirólisis de cáscara de naranja y maderas ecuatorianas.22,24
El objetivo de este trabajo es estudiar la influencia de la velocidad de calentamiento y el tipo de biomasa en los parámetros cinéticos (energía de activación y modelo cinético), durante la descomposición pirolítica de las maderas ecuatorianas Teca y Guachapelí, utilizando análisis no isotérmico y el método de ajuste de las funciones.
Materiales y métodos
Las maderas ecuatorianas Teca y Guachapelí, proceden del Centro de Comercialización ubicado en Portoviejo, Manabí, República del Ecuador. Allí el tronco es acerado y preparado para su comercialización, en dependencia de sus diferentes usos. Las muestras objeto de estudio forman parte de los residuos forestales de dicho centro y se escogieron cuidadosamente en forma de pequeños trozos, paralograr una muestra representativa.
Análisis inmediato
Para el análisis inmediato: la humedad,Norma UNE-EN-14774-1:2010 25 y materia volátil, Norma UNE-EN-15148:2010 26, se determinan a través de un TGA Q500 TA Instruments, el poder calórico superior se realiza en un calorímetro Parr 6300,utilizando muestras de 1+/-0.5 g por triplicado, para garantizar su repetividad.
Análisis térmico convencional
Las curvas termogravimétricas analizadas se obtuvieron en un equipo TGA Q500 TA Instruments. Se utilizaron dos velocidades de calentamiento 15 y 95 °C/min, con un flujo de nitrógeno de 60 ml/min para garantizar la atmósfera inerte y masa de muestras de 0.5mg.
Análisis térmico simultáneo
El análisis térmico se efectuó en un equipo NETZSCH STA 449F3m con técnicas TGA, ATD y DSC combinadas. Se utiliza la velocidad de calentamiento 10 °C/min, un flujo de nitrógeno de 60 ml/min para garantizar la atmósfera inertey muestras de 0,5 mg. La obtención de los gráficos se realizó con el software Origin 6.1.
Estudio cinético
Al aplicar el método de ajuste de las funciones, tanto en su forma integral como derivada, para la determinación de los coeficientes de correlación lineal (r) se utiliza el software Microsoft Excel 2010, lo que permite identificar los modelos cinéticos que determinan la velocidad de reacción. Para el cálculo de los parámetros cinéticos energía de activación y modelo cinético se emplea el software Origin 6.1.
Metodología de cálculo utilizada
La metodología de cálculo utilizada ha sido explicada.22-24 De forma general, el método se basa en el ajuste por correlación estadística de una serie de modelos matemáticos (diferenciales o integrales) que describen los modelos cinéticos de reacción (tabla 1).
Para el estudio cinético se escogieron las ecuaciones de Coats-Redfern (método integral) y la ecuación de Achar (método diferencial), las que se explican a continuación.
Método de Coats-Redfern
Graficando el miembro izquierdo con respecto a 1/T, se obtiene E y Z de la pendiente y el intercepto respectivamente, para el modelo que muestre el mejor ajuste linear.
Método de Achar o Método diferencial directo
Al graficar el miembro izquierdo vs. 1000/T para cada función f (α), el modelo cinético que mejor describe la reacción es seleccionado a partir de los valores del coeficiente de regresión (r). Entonces, el valor de la pendiente estará relacionado con el término E/R y el intercepto permite calcular Z.22-24
Resultados y discusión
El análisis inmediato de las maderas estudiadas es presentado en la tabla 2. Los contenidos de humedad menor al 10 % para ambas maderas, las convierten en atractivas para su termoconversión a través de pirólisis.
Tabla 2 Resultados del análisis inmediato de Teca y Guachapelí su comparación con resultados de otros autores.
| Teca | Guachapelí | Teca Nigeriana27 | |
| Humedad (%) | 3,80 | 4,90 | - |
| Volátiles (%) | 76,77 | 72,27 | - |
| Carbón fijo (%) | 17,68 | 14,56 | 3,8 |
| Cenizas (%) | 1,75 | 2,77 | 0,7 |
| Poder calorífico superior (MJ/Kg) | 19,07 | 19,77 | 19,8 |
La porción de combustible que se libera en forma de gases, es decir, los componentes volátiles para ambas maderas ecuatorianas se encuentran en el rango reportado para biomasa maderera (60-80 %). Los contenidos de volátiles y carbón fijo en estos residuos ecuatorianos, explican el poder calórico de las biomasas. En relación a las cenizas, estas poseen bajos contenidos, lo que resulta esperado en biomasa maderera, garantizando la menor evolución de material particulado y reduce la posibilidad de formación de incrustaciones en los equipos, de ser utilizada con fines energéticos.
En la figura 1 se muestra la influencia de la velocidad de calentamiento, en el perfil pirolítico de las maderas ecuatorianas. Un incremento de éstade 15 a 95(C, para cada madera, tiende a desplazar la temperatura máxima (es la temperatura a la cual la velocidad de pérdida de masa es máxima), durante el proceso de degradación de ambas maderas, como se observa en la figura. Varios autores han indicado que las reacciones de conversión de biomasa, son cinéticamente más lentas a mayor tasa de calentamiento.16-17) Además, se incrementa la velocidad de degradación térmica, lo que resulta lógico porque se le suministra más calor a la muestra en menor tiempo y porque aumenta la producción de la materia volátil. Relacionado con esto último, Damartzis y colaboradores explican que cuando la velocidad de calentamiento es alta, se alcanza un flujo calórico alto que reduce la viscosidad de la materia sólida fundida, lo que intensifica la reacción de formación de volátiles.24 Para ambas velocidades de calentamiento se observa que Teca tiene mayor velocidad de degradación, lo que coincide con la mayor materia volátil identificada por análisis inmediato en ella.
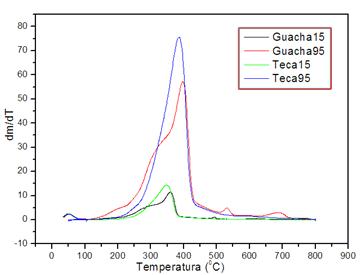
Fig. 1 Efecto de la velocidad de calentamiento sobre el perfil pirolítico DTG de Teca y Guachapelí. Negro Guachapelí 15°C/min, Rojo Guachapelí 95°C/min, Verde Teca 15°C/min y Azul Teca 95°C/min.
En la figura 2 se presenta el efecto de la velocidad de calentamiento en las curvas TGA para ambas maderas. Vuelve a observarse el desplazamiento del perfil térmico hacia temperaturas mayores, cuando se incrementa la (. A partir del tramo isotérmico de las curvas estudiadas, se distingue una similar estabilidad térmica en ambas maderas, para las dos (. Aunque no se distinguen en las curvas una diferente degradación pirolítica en ambas maderas, se demuestra la mayor cantidad de carbón fijo identificada en Teca, a través del análisis inmediato.
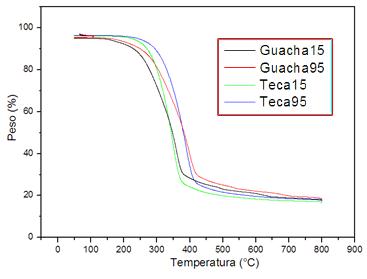
Fig. 2 Efecto de la velocidad de calentamiento sobre el perfil pirolítico TGA de Teca y Guachapelí. Negro Guachapelí 15°C/min, Rojo Guachapelí 95°C/min, Verde Teca 15°C/min y Azul Teca 95°C/min.
Análisis cinético del craqueo pirolítico de las biomasas investigadas
La interpretación de los registros térmicos de las maderas objeto de estudio (figuras 1 y 2), tanto desde el punto de vista cualitativo como cuantitativo, ha sido objeto de análisis en otros trabajos 23-24, por lo que en este artículo centraremos la atención en el efecto de la velocidad de calentamiento y el tipo de biomasa en los parámetros cinéticos calculados.
El estudio cinético del craqueo pirolítico de la biomasa, identifica la etapa más lenta que determina la velocidad de la reacción. Cuando se aborda esta cinética, una gran diversidad de criterios y expresiones matemáticas para llevar acabo este estudio, han sido propuestas. Todos coinciden en la complejidad de este proceso, debido a la diversidad de biomasas existentes, a que en todas ellas predomina la presencia de tres constituyentes fundamentales que se degradan térmicamente, a la ocurrencia de reacciones principales y secundarias que pueden ocurrir de forma paralela o independiente y a los complejos procesos de transferencia de masa y energía que tienen lugar, entre otros aspectos.16-24
Algunos autores prefieren trabajar de forma global o dividir el proceso en cuatro etapas fundamentales, relacionadas con la deshidratación de la biomasa y la descomposición térmica de los componentes mayoritarios. En este trabajo nos acogemos a la segunda vía, pues es evidente que abordar el estudio cinético por etapas, si bien es mucho más complicado y laborioso, permite un estudio más detallado del proceso pirolítico. Además, el estudio cinético fue diseñado para abordar una única reacción, por tanto, al dividir el proceso pirolítico por etapas se logran resultados cinéticos más específicos y representativos de las reacciones individuales que tienen lugar, dentro de ese proceso complejo. Cuando se estudian reacciones que involucran varias etapas, como una etapa única, los parámetros cinéticos calculados son globales y representan a todo el proceso en su conjunto. Por último, varios autores refieren que el método de 3 Reacciones Paralelas Independiente 21) está ofreciendo mejores resultados y en este trabajo se parte de ese criterio, aunque el cálculo se realiza de forma diferente.
A continuación se discuten los resultados obtenidos al abordar el efecto de la velocidad de calentamiento y el tipo de biomasa, en la cinética de las principales etapas involucradas en este proceso, devolatilización de hemicelulosa, celulosa y lignina, auxiliándose para ello de los intervalos de temperatura ya precisados 23-24, en donde prevalecen la ocurrencia de las reacciones propuestas. El cálculo cinético se realiza utilizando el método de ajuste de las funciones y en particular las ecuaciones de Coats (Integral) y Achar (Diferencial).
De forma general, para la selección de los parámetros cinéticos y del modelo cinético en primera instancia, a una velocidad de calentamiento determinada, se utiliza el criterio del coeficiente de correlación lineal cercano a uno, debido a que las ecuaciones cinéticas utilizadas responden a una línea recta. Cuando para una reacción o etapa del proceso en particular, varios modelos presentan valores de r cercanos entre ellos, se considera hasta un Δr =0,06 para distinguir los modelos probables, dentro de una misma ecuación cinética, en este caso Coats o Achar. Luego de identificado estos modelos, se comparan los resultados obtenidos para ambas ecuaciones cinéticas (Coats y Achar) y se escogen los modelos cinéticos que se repiten, como los que determinan la velocidad de la reacción, para esa etapa del proceso de descomposición pirolítica. Una vez seleccionado el modelo cinético, se calcula la Energía de activación a partir de la pendiente de esa recta, como ya fue referido. Esta metodología de cálculo ha sido propuesta y utilizada por Quesada y colaboradores en el estudio de la pirólisis de la cáscara de naranja, maderas ecuatorianas y marabú cubano. 23-24
Las tablas 3, 4 y 5 muestran los resultados obtenidos al estudiar la cinética de la descomposición de los constituyentes principales de Teca a 15 y 95°C/min respectivamente. Los modelos a la izquierda en dichas tablas, son los seleccionados para la (= 15°C/min y los de la derecha para la (= 95°C/min, en vista que se pretende demostrar la influencia o no de la velocidad de calentamiento, en los resultados cinéticos.
Tabla 3 Descomposición pirolítica de la hemicelulosa, parámetros cinéticos calculados al utilizar el método de ajuste de las funciones y dos velocidades de calentamiento
| Teca -Hemicelulosa | ||||||||||
| 15 °C/min | 95 °C/min | |||||||||
| Método Coats | Método Achar | Método Coats | Método Achar | |||||||
| Modelo | R | Ea | R | Ea | R | Ea | R | Ea | Modelo | |
| D1 | 0,92 | 222 | 0,97 | 187 | 0,93 | 202 | 0,97 | 168 | D1 | |
| D2 | 0,93 | 232 | 0,98 | 205 | 0,94 | 212 | 0,98 | 185 | D2 | |
| D3 | 0,94 | 244 | 0,97 | 225 | 0,95 | 225 | 0,98 | 205 | D3 | |
| D4 | 0,93 | 236 | 0,56 | 42 | 0,95 | 216 | 0,62 | 33 | D4 | |
| F1 | 0,94 | 124 | 0,89 | 112 | 0,96 | 114 | 0,89 | 102 | F1 | |
| R1 | 0,91 | 107 | 0,99 | 72 | 0,92 | 97 | 0,99 | 63 | R1 | |
| R2 | 0,93 | 105 | 0,95 | 92 | 0,94 | 105 | 0,95 | 82 | R2 | |
| R3 | 0,94 | 118 | 0,93 | 99 | 0,95 | 108 | 0,93 | 89 | R3 | |
| A 0,5 | 0,90 | 216 | 0,96 | 245 | 0,92 | 197 | 0,97 | 225 | A 0,5 | |
| A1 | 0,75 | 83 | 0,89 | 112 | 0,76 | 74 | 0,89 | 102 | A1 | |
| A2 | 0,14 | 17 | 0,56 | 46 | 0,10 | 13 | 0,54 | 41 | A2 | |
| A3 | 0,01 | 45 | 0,24 | 24 | 0,04 | 8 | 0,21 | 21 | A3 | |
| A4 | 0,14 | 16 | 0,08 | 13 | 0,21 | 18 | 0,06 | 10 | A4 | |
Coats: 107 - 244 kJ/mol Achar: 72 - 245 kJ/mol a 15 °C/min
Coats: 97 - 225 kJ/mol Achar: 62- 225 kJ/mol a 95 °C/min
Aunque el estudio cinético se realiza por separado para ambas velocidades de calentamiento, van a ser discutidos de forma conjunta, aunque partan de un análisis individual, en aras de ser más concretos en dicho análisis.
A partir de los criterios ya referidos se seleccionan para ambas velocidades de calentamiento (tabla 3), los modelos D1, D2, D3, R1, R2, R3 y A0.5, como los que determinan la velocidad de descomposición de la hemicelulosa, por ser los que se repiten entre los más probables para las ecuaciones cinéticas utilizadas. Estos modelos están más relacionados con procesos difusivos (D) y avance de la interfase de reacción (R) y un único modelo de nucleación (A0.5). Resultados similares han sido reportados para las maderas Fernán Sánchez ecuatoriana (D1, D2, D3 y A0.5) 23 y Marabú cubano (D1, D2, D3, F1, R1, R2, R3 y A0,5).24 Resalta la gran coincidencia entre los parámetros cinéticos calculados para ambas velocidades, lo que no ocurre en las etapas de descomposición de celulosa y lignina.
Se demuestra que esta etapa de devolatilización presenta una cinética compleja, porque varios modelos muestran coeficientes de correlación muy cercanos a uno. En nuestra consideración, esta dificultad puede estar atribuida a que, aunque en este intervalo de temperatura (210-310°C) prevalece principalmente la ecuación de descomposición de la hemicelulosa, por ser el constituyente más inestable térmicamente de la biomasa, debido a su estructura. A temperaturas cercanas a 200°C puede iniciar también en menor proporción la descomposición de los fragmentos más volátiles de la lignina. Otros autores han simulado teóricamente estos procesos de descomposición pirolítica de los principales constituyentes de la biomasa por separado y han propuesto intervalos para la lignina entre 200-500°C 27 y 200-600 °C.28 Sin descartar, que pueda iniciarse también el proceso de descomposición de la celulosa, así como otras reacciones que ocurren al margen de la devolatilización de los constituyentes principales. Esta diversidad de reacciones químicas ocurriendo en mayor o menor medida, hacen de esta etapa la más compleja y esa misma diversidad propicia que varios modelos cinéticos se ajusten a los datos experimentales. Aunque vale resaltar que en su mayoría corresponden a modelos difusivos y de avance de la interfase de la reacción, que son los identificados en otras maderas. La mayor parte de los autores suponen a priori que el modelo cinético es F1 o no lo precisan en sus estudios cinéticos.
Los valores de energías de activación para esta etapa se encuentran entre 72-245kJ/mol a 15 °C/min y 62-225 kJ/mol a 95°C/min, no encontrándose tampoco grandes diferencias para ambas velocidades. Quesada y colaboradores reportaron para el marabú entre 89-272 kJ/mol.24
La tabla 4 muestran los resultados cinéticos a 15 y 95°C/min respectivamente, de la devolatilización de la celulosa contenida en Teca. A partir de los criterios explicados para la selección, en el caso de la primera (, F1 es el único modelo elegido, a diferencia de la segunda velocidad de calentamiento estudiada que son D1, D2, D3 y R2, R3. Quesada y colaboradores encontraron para Fernán Sánchez en esta etapa, los modelos F1, A0.5 y A3.23) Se demuestra que no hay coincidencia entre los modelos cinéticos seleccionados para ambas β, en esta investigación.
Los valores de energía de activación están entre 109-155 kJ/mol a 15°C/min y 86-286 kJ/mol a 95°C/min.Fue reportado entre 146 -215 kJ/mol para Fernán Sánchez a 10°C/min.23 Estos resultados demuestran que la velocidad de calentamiento también influye en los valores de Ea de la degradación de celulosa.
Tabla 4 Descomposición pirolítica de la celulosa, parámetros cinéticos calculados al utilizar el método de ajuste de las funcionesy dos velocidades de calentamiento.
| Teca - Celulosa | ||||||||||
| 15 °C/min | 95 °C/min | |||||||||
| Método Coats | Método Achar | Método Coats | Método Achar | |||||||
| Modelo | R | Ea | R | Ea | R | Ea | R | Ea | Modelo | |
| D1 | 0,75 | 202 | 0,08 | 38 | 0,88 | 244 | 0,92 | 173 | D1 | |
| D2 | 0,80 | 229 | 0,46 | 98 | 0,90 | 263 | 0,96 | 207 | D2 | |
| D3 | 0,87 | 270 | 0,87 | 190 | 0,93 | 286 | 0,97 | 248 | D3 | |
| D4 | 0,82 | 241 | 0,35 | 75 | 0,91 | 270 | 0,03 | 11 | D4 | |
| F1 | 0,92 | 156 | 0,89 | 109 | 0,94 | 150 | 0,88 | 126 | F1 | |
| R1 | 0,73 | 96 | 0,48 | 68 | 0,86 | 117 | 0,96 | 46 | R1 | |
| R2 | 0,83 | 119 | 0,19 | 20 | 0,91 | 132 | 0,95 | 86 | R2 | |
| R3 | 0,86 | 130 | 0,65 | 50 | 0,92 | 138 | 0,93 | 99 | R3 | |
| A 0,5 | 0,48 | 145 | 0,95 | 275 | 0,84 | 230 | 0,96 | 287 | A 0,5 | |
| A1 | 0,04 | 22 | 0,89 | 109 | 0,48 | 70 | 0,88 | 126 | A1 | |
| A2 | 0,56 | 105 | 0,25 | 26 | 0,02 | 10 | 0,43 | 46 | A2 | |
| A3 | 0,70 | 132 | 3E-05 | 2 | 0,28 | 37 | 0,10 | 20 | A3 | |
| A4 | 0,75 | 146 | 0,08 | 16 | 0,43 | 51 | 0,003 | 6 | A4 | |
Coats: 156kJ/mol Achar: 109kJ/mol a 15 °C/min
Coats: 132 - 286kJ/mol Achar: 86- 248kJ/mola 95 °C/min
Tabla 5 Descomposición pirolítica de la lignina, parámetros cinéticos calculados al utilizar el método de ajuste de las funciones y dos velocidades de calentamiento
| Teca - Lignina | ||||||||||
| 15 °C/min | 95 °C/min | |||||||||
| Método Coats | Método Achar | Método Coats | Método Achar | |||||||
| Modelo | R | Ea | R | Ea | R | Ea | R | Ea | Modelo | |
| D1 | 0,60 | 93 | 0,04 | 8 | 0,39 | 37 | 0,86 | 46 | D1 | |
| D2 | 0,67 | 108 | 0,57 | 40 | 0,51 | 51 | 0,30 | 14 | D2 | |
| D3 | 0,76 | 131 | 0,81 | 88 | 0,68 | 73 | 0,47 | 36 | D3 | |
| D4 | 0,70 | 115 | 0,88 | 140 | 0,57 | 57 | 0,93 | 244 | D4 | |
| F1 | 0,81 | 73 | 0,48 | 46 | 0,75 | 44 | 0,16 | 25 | F1 | |
| R1 | 0,52 | 40 | 0,93 | 45 | 0,21 | 12 | 0,84 | 72 | R1 | |
| R2 | 0,67 | 53 | 3E-04 | 1 | 0,49 | 24 | 0,24 | 24 | R2 | |
| R3 | 0,72 | 59 | 0,17 | 16 | 0,59 | 30 | 0,02 | 8 | R3 | |
| A 0,5 | 0,37 | 67 | 0,85 | 132 | 0,00 | 5 | 0,70 | 82 | A 0,5 | |
| A1 | 0,09 | 18 | 0,48 | 46 | 0,60 | 53 | 0,16 | 25 | A1 | |
| A2 | 0,61 | 61 | 3E-03 | 4 | 0,82 | 81 | 0,02 | 3 | A2 | |
| A3 | 0,73 | 75 | 0,03 | 11 | 0,85 | 91 | 0,03 | 12 | A3 | |
| A4 | 0,77 | 82 | 0,09 | 18 | 0,87 | 95 | 0,06 | 17 | A4 | |
Coats: 73 - 131 kJ/mol Achar: 45 - 140 kJ/mol a 15 °C/min
Coats: 81 - 95kJ/mol Achar: 3 - 244kJ/mol a 95 °C/min
Por último, la etapa de descomposición de la lignina contenida en la biomasa investigada, cuyos resultados cinéticos se presentan en la tabla 5. Para la β=15°C/min los modelos cinéticos seleccionados son D3, D4, F1, R1, A4 y para β=95°C/min son D4, A2, A3 y A4. Para el Marabú cubano y Fernán Sánchez ecuatoriana, se precisaron en esta etapa los modelos D2 y D3.23-24 Los valores de energía de activación son de 45- 140 kJ/mol para15°C/min y de 81-244kJ/mol para 95°C/min, los mismos concuerdan con los propuestos por otros autores.Para Fernán Sánchez se precisó un intervalo entre 83-153kJ/mol.23 Vuelven a identificarse en este trabajo, la influencia de la tasa de calentamiento en los parámetros cinéticos calculados.
En las tablas 6, 7 y 8 se representan los resultados del estudio cinético de la pirólisis de la madera Guachapelí, cuando se aplican las ecuaciones de Coats y Achar, para las etapas ya precisadas de descomposición de los constituyentes fundamentales de la biomasa y las dos velocidades de calentamiento.
Tabla 6 Descomposición pirolítica de la hemicelulosa, parámetros cinéticos calculados al utilizar el método de ajuste de las funciones y dos velocidades de calentamiento.
| Guachapelí -Hemicelulosa | ||||||||||
| 15 °C/min | 95 °C/min | |||||||||
| Método Coats | Método Achar | Método Coats | Método Achar | |||||||
| Modelo | R | Ea | R | Ea | R | Ea | R | Ea | Modelo | |
| D1 | 0,90 | 192 | 0,95 | 149 | 0,90 | 165 | 0,96 | 127 | D1 | |
| D2 | 0,91 | 203 | 0,97 | 170 | 0,92 | 176 | 0,98 | 146 | D2 | |
| D3 | 0,93 | 218 | 0,97 | 196 | 0,93 | 190 | 0,97 | 170 | D3 | |
| D4 | 0,92 | 208 | 0,07 | 12 | 0,92 | 181 | 0,00 | 3 | D4 | |
| F1 | 0,94 | 113 | 0,88 | 99 | 0,94 | 98 | 0,82 | 85 | F1 | |
| R1 | 0,89 | 92 | 0,99 | 49 | 0,89 | 78 | 0,97 | 40 | R1 | |
| R2 | 0,92 | 101 | 0,95 | 74 | 0,92 | 87 | 0,89 | 63 | R2 | |
| R3 | 0,93 | 105 | 0,92 | 82 | 0,93 | 91 | 0,86 | 70 | R3 | |
| A 0.5 | 0,87 | 183 | 0,96 | 220 | 0,87 | 158 | 0,95 | 192 | A 0,5 | |
| A1 | 0,60 | 62 | 0,88 | 99 | 0,60 | 52 | 0,82 | 85 | A1 | |
| A2 | 0,00 | 2 | 0,48 | 39 | 0,01 | 2 | 0,37 | 33 | A2 | |
| A3 | 0,16 | 18 | 0,16 | 18 | 0,22 | 19 | 0,10 | 15 | A3 | |
| A4 | 0,32 | 28 | 0,03 | 9 | 0,38 | 28 | 0,01 | 6 | A4 | |
Coats: 92 - 218 KJ/mol Achar: 74 - 220KJ/mol a 15 °C/min
Coats: 78 - 190KJ/mol Achar: 40 - 170KJ/mol a 95 °C/min
En el caso de la etapa de devolatilización de la hemicelulosa (tabla 6), se identifican a 15 C(/min los modelos cinéticos D1,D2,D3,R1,R2,R3 y A0,5 y para 95 C(/min los modelos D1,D2,D3,R1 y R2. Vuelven a precisarse los modelos difusivos y los de avance de la interfase, como los que más prevalecen fundamentalmente en esta etapa. Estos resultados también evidencian la complejidad de los procesos de pirólisis de biomasa, objeto de estudio. Fueron calculados los valores de Ea entre 74,1-220,3 kJ/mol a 15°C/min y 40-190,3 kJ/mol a 95 °C/min. A diferencia de la madera Teca, en Guachapelí se obtienen diferentes modelos cinéticos y valores de Ea para esta etapa, a ambas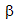 .
.
Para la etapa del craqueo pirolítico de la celulosa (tabla 7) a 15C(/min se escogen los modelos D3 y F1 y a 95C(/min los modelos difusivos D1, D2 y D3, como etapas limitantes del proceso en estudio.Para Teca se obtuvieron los modelos F1 y D1,D2,D3,R2,R3 para 15 y 95C(/min respectivamente. Para Fernán Sánchez se identificaron los modelos F1, A0.5, A3 23) y para el marabú D3,F1,R3,A0.5,A3,A4.24 Vale destacar que esta es la única etapa del proceso de devolatilización de biomasa, donde prevalece el modelo F1, aunque no sea el único. Esto último demuestra el error de suponer a priori este modelo cinético. Los valores de energía de activación calculados en este proceso se encuentran entre 116-267 y 132-244 kJ/mol para 15 y 95 °C/min respectivamente. Vuelve a demostrarse la influencia de la (en los parámetros cinéticos calculados, si bien puede enmarcarse que el efecto es mayor en el modelo cinético.
Tabla 7 Descomposición pirolítica de la celulosa, parámetros cinéticos calculados al utilizar el método de ajuste de las funciones y dos velocidades de calentamiento.
| Guachapelí -Celulosa | ||||||||||
| 15 °C/min | 95 °C/min | |||||||||
| Método Coats | Método Achar | Método Coats | Método Achar | |||||||
| Modelo | R | Ea | R | Ea | R | Ea | R | Ea | Modelo | |
| D1 | 0,79 | 203 | 0,26 | 63 | 0,84 | 203 | 0,90 | 132 | D1 | |
| D2 | 0,84 | 228 | 0,65 | 119 | 0,87 | 221 | 0,95 | 164 | D2 | |
| D3 | 0,90 | 267 | 0,92 | 201 | 0,90 | 244 | 0,95 | 203 | D3 | |
| D4 | 0,86 | 240 | 0,26 | 56 | 0,88 | 228 | 0,40 | 41 | D4 | |
| F1 | 0,94 | 152 | 0,89 | 116 | 0,91 | 129 | 0,78 | 102 | F1 | |
| R1 | 0,77 | 96 | 0,30 | 43 | 0,82 | 97 | 0,94 | 25 | R1 | |
| R2 | 0,86 | 119 | 0,48 | 36 | 0,88 | 111 | 0,82 | 63 | R2 | |
| R3 | 0,89 | 128 | 0,78 | 63 | 0,89 | 117 | 0,80 | 76 | R3 | |
| A 0.5 | 0,57 | 154 | 0,95 | 278 | 0,79 | 190 | 0,94 | 241 | A 0,5 | |
| A1 | 0,00 | 89 | 0,89 | 116 | 0,37 | 52 | 0,78 | 102 | A1 | |
| A2 | 0,49 | 89 | 0,33 | 35 | 0,09 | 18 | 0,23 | 33 | A2 | |
| A3 | 0,64 | 115 | 0,02 | 8 | 0,38 | 41 | 0,02 | 10 | A3 | |
| A4 | 0,70 | 129 | 0,01 | 6 | 0,51 | 53 | 0,01 | 2 | A4 | |
Coats: 152 - 267KJ/mol Achar: 116 - 201KJ/mol a 15 °C/min
Coats: 203 - 244KJ/mol Achar: 132 - 203KJ/mol a 95 °C/min
Tabla 8 Descomposición pirolítica de la lignina, parámetros cinéticos calculados al utilizar el método de ajuste de las funciones y y dos velocidades de calentamiento
| Guachapelí - Lignina | ||||||||||
| 15 °C/min | 95 °C/min | |||||||||
| Método Coats | Método Achar | Método Coats | Método Achar | |||||||
| Modelo | R | Ea | R | Ea | R | Ea | R | Ea | Modelo | |
| D1 | 0,64 | 100 | 0,14 | 17 | 0,39 | 42 | 0,72 | 41 | D1 | |
| D2 | 0,71 | 115 | 0,58 | 49 | 0,51 | 55 | 0,09 | 9 | D2 | |
| D3 | 0,79 | 138 | 0,80 | 92 | 0,67 | 78 | 0,53 | 43 | D3 | |
| D4 | 0,74 | 122 | 0,81 | 136 | 0,57 | 62 | 0,95 | 218 | D4 | |
| F1 | 0,83 | 75 | 0,45 | 45 | 0,74 | 47 | 0,21 | 29 | F1 | |
| R1 | 0,58 | 44 | 0,73 | 39 | 0,23 | 15 | 0,80 | 69 | R1 | |
| R2 | 0,41 | 57 | 0.01 | 3 | 0,49 | 27 | 0,17 | 20 | R2 | |
| R3 | 0,75 | 62 | 0,15 | 17 | 0,59 | 33 | 0,00 | 4 | R3 | |
| A 0,5 | 0,46 | 78 | 0,85 | 133 | 0,01 | 8 | 0,72 | 90 | A 0,5 | |
| A1 | 0,03 | 9 | 0,44 | 45 | 0,56 | 52 | 0,21 | 29 | A1 | |
| A2 | 0,60 | 53 | 0,00 | 2 | 0,80 | 82 | 0,00 | 1 | A2 | |
| A3 | 0,74 | 68 | 0,04 | 13 | 0,84 | 92 | 0,02 | 10 | A3 | |
| A4 | 0,79 | 75 | 0,10 | 21 | 0,86 | 97 | 0,04 | 15 | A4 | |
Coats: 137 kJ/mol Achar: 92 -136 kJ/mol a 15 °C/min
Coats: 82 - 97 kJ/mol Achar: 218 kJ/mol a 95 °C/min
Para la última etapa de descomposición de la biomasa (tabla 8) bajo atmósfera inertea 15 C(/minel modelo D3y 95 C(/min los D4, A2, A3 y A4 son los de mayor coeficiente de correlación.Los valores de energía de activación se encuentran en los intervalos de 92-137 kJ/mol y 82-218 kJ/mol respectivamente. Para la madera Fernán Sánchez los modelos que prevalecen son D2, D3 y la Ea fue entre 83-153 kJ/mol y para Teca fueron D3,D4,F1,R1,A4 y D4,A2,A3,A4 para 15 y 95C(/min respectivamente.23-24) Llama la atención que solo en esta etapa de la lignina, para ambas biomasas, en algunas (, no hay coincidencia entre los modelos cinéticos identificados por Coats y Achar. Las pocas veces que esto ha ocurrido se escogen todos los modelos como posibles y demuestra la validez de la metodología de cálculo aplicada. Recuerde que la mayor parte de los autores realizan el estudio cinético utilizando una única expresión matemática y condiciones experimentales.
Influencia de la velocidad de calentamiento y la biomasa en la cinética de la descomposición pirolítica de Teca y Guachapelí
En la tabla 9 se resumen los resultados cinéticos de la pirólisis de Teca y Guachapelí, cuando se descompone la biomasa a 15 y 95 °C/min.
Tabla 9 Influencia de la β y la biomasa en la cinética de la pirólisis de Teca
| Etapas | Biomasas | Β (°C/min) | Parámetros Cinéticos | ||
| Modelo Cinético | Ea (kJ/mol) | ||||
| Hemicelulosa | Teca | 15 | D1,D2,D3,R1,R2,R3,A0,5 | 72-245 | |
| 95 | D1,D2,D3,R1,R2,R3,A0,5 | 62-225 | |||
| Guachapelí | 15 | D1,D2,D3,R1,R2,R3,A0,5 | 74-220 | ||
| 95 | D1,D2,D3,R1,R2 | 40-190 | |||
| Celulosa | Teca | 15 | F1 | 109-155 | |
| 95 | D1,D2,D3,R2,R3 | 86-286 | |||
| Guachapelí | 15 | D3,F1 | 115-266 | ||
| 95 | D1,D2,D3 | 132-244 | |||
| Lignina | Teca | 15 | D3,D4,F1,R1,A4 | 45-140 | |
| 95 | D4,A2,A3,A4 | 2,9-244 | |||
| Guachapelí | 15 | D3 | 92-137 | ||
| 95 | D4,A2,A3,A4 | 81-218 | |||
Cuando se realiza un estudio cinético con un fin más relacionado con la ciencia, se prefiere trabajar a bajas velocidades, porque se logra un mejor control de los gradientes de temperatura y presión que propician alcanzar resultados cinéticos reproducibles. Sin embargo, para la industria, los procesos químicos a bajas β son largos, engorrosos y caros, de ahí la preferencia de los tecnólogos a utilizar altas β. En la actualidad lo que ocurre es que se extrapolan y utilizan resultados cinéticos obtenidos a bajas β a escalados tecnológicos, en los que se emplean velocidades de calentamiento mayores. Esto solo puede ser justificable si la β y la biomasa no influyen en la cinética del proceso estudiado.
En tabla 9 se demuestra de forma general, que la velocidad de calentamiento y el tipo de biomasa influyen en los parámetros cinéticos calculados, es decir, ejercen efecto tanto en el modelo cinético, como en la energía de activación. Después de este resultado se demuestra que es cuestionable realizar generalizaciones de parámetros cinéticos, cuando se trabaja con diferentes β y biomasas. En lo que respecta a la β, este parámetro no solo puede variar la cinética, sino hasta el tipo de reacción que ocurre y los productos finales de la misma.11,16
La diversidad de los parámetros cinéticos calculados, incluso para una única etapa de devolatilización de la biomasa, demuestra la complejidad cinética de estos procesos de craqueo pirolítico y la dificultad de precisar el modelo cinético que determina dicho proceso. Razón por la cual, la mayor parte de los investigadores obvian ese parámetro. Además, se demuestra que los modelos cinéticos difusivos se repiten entre los posibles para las tres etapas de descomposición de la biomasa y solo en excepciones el F1 (crecimiento unimolecular) es el único que prevalece, lo que demuestra el error de suponer a priori que este es el modelo que determina la velocidad de reacción, aspecto que es ampliamente difundido en esta temática.
Conclusiones
El estudio cinético realizado identificó los modelos cinéticos y los valores de energía de activación para la devolatilización de hemicelulosa, celulosa y lignina para Teca y Guachapelí, demostrándose que no se debe escoger a priori el modelo F1 como el determinante.Se demuestra la influencia de la velocidad de calentamiento y del tipo de biomasa en los resultados cinéticos obtenidos, por lo tanto, no deben extrapolarse resultados de bajas a altas velocidades de calentamiento