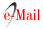Original article

Offside rule: the assistant referee's condemnation

0000-0002-6643-8940Fernando Correa Alsina^{1  *} 

¹Universidad de la República. Facultad de Ciencias Sociales. Departamento de Economía Montevideo, Montevideo Uruguay.

ABSTRACT

Introduction:

in this article, a model is developed that includes the main elements of a typical game situation in which the assistant referee must judge a possible offside. In this conceptual framework, the assumption is incorporated that the assistant makes a change of gaze and can only evaluate the relative position of the attacker with respect to the penultimate opponent thousandths of seconds after the pass..

Objective:

to identify the determinants of the degree of difficulty that exists for the assistant referee to correctly judge a possible offside.

Material and methods:

analytical-synthetic and systemic structural-functional methods were used as theoretical methods of scientific research. From the empirical ones, documentary analysis and expert judgment, as well as estimates based on geometric calculations.

Results:

it is shown that in most cases the assistant referee must make a decision at the precise moment in which the distortion derived from the change of gaze reaches its maximum expression.

Conclusions:

the estimates made for different situations allow the model's derivations to be verified and quantified.

Key words: offside; assistant referee; soccer.

INTRODUCTION

The offside penalty is one of the most controversial aspects of soccer. Although the regulations are clear and establish an apparently simple rule, its practical application give rise too many erroneous rulings, as well as discussions between players and referees, in which journalists and fans also participate.

Law 11 of the rules governing soccer worldwide establishes that a player is in an offside position when he is wholly or partially in the opponents' half of the field of play and closer to the opponents' goal line than the ball and the second last opponent. The hands and arms of the players shall not be taken into consideration for this determination.

However, being in an offside position does not constitute an offence. A player who is offside, at the time the ball touches or is played by a teammate, is only be penalized if he becomes actively involves in play. An offside offence is not sanctioned when the ball comes directly from a goal kick, throw-in or corner kick ^{(International Football Association Board, 2023)}.

This Rule underwent few modifications throughout its long history and all of them were aimed at facilitating the work of the attacking team. In its first version of 1863, it established that attacking players who were in front of the ball line, at the time of the pass, were out of play and could not touch the ball or prevent another player from doing so. Three years later, the Rule was modified allowing the attacker to touch the ball or participate in play, in such circumstances, if there were at least three opposing players located closer to the goal line. In 1925, this requirement was reduced to only two players. Finally, in 1990 the attacking player was allowed to be on the same line as the penultimate opponent ^{(Carosi, 2010}; ^{Clark, 2016)}.

Over the past 25 years, a significant number of studies have been carried out on offside, aimed both at quantifying the errors committed and identifying their main causes. Regarding the first aspect, research shows that between 13% and 26% of refereeing decisions are erroneous, considering as such both those not sanctioned (non-flag errors) and those wrongly sanctioned (flag errors) ^{(Catteeuw et al.,2010}; ^{Helsen et al., 2006}; ^{Mallo et al., 2012)}. The importance of the errors made prompted the introduction of the video refereeing (Video Assistant Referees - VAR) in 2018 ^{(International Football Association Board, 2018)}. However, this technological tool is of optional use and is only used in a smaller set of competitions held worldwide.

On the second aspect, three main hypotheses have been developed that would explain the causes of refereeing errors. It should be noted that, although a debate has been generated, based on empirical evidence, among the advocates of the different hypotheses, they are not mutually exclusive.

The first hypothesis states that refereeing errors are due to the shift of gaze (shift of gaze hypothesis) that the assistant referee must perform, at the time of the pass, from the player who makes the pass to the last defender (without considering the goalkeeper), simultaneously evaluating the relative position of the attacker receiving the ball. This change of gaze determines that the offside judgment is made milliseconds after the pass, when the relative positions of the players may have been altered ^{(Belda Maruenda, 2004}; ^{Sanabria et al., 1998)}.

In support of this hypothesis, evidence has been found that refereeing errors are more frequent when, from the position of the assistant referee, a relatively wide angle is formed between the player passing the ball and the last defender. However, it has not been possible to verify a positive correlation between the two variables mentioned ^{(Hüttermann et al., 2017}; ^{Mallo et al., 2012)}.

According to the second hypothesis, the problem originates in an optical error (optical error hypothesis) derived from an inadequate positioning of the assistant referee at the time of the pass, positioned outside the offside line, that is, the line parallel to the goal line that passes through the last defender. When the assistant referee is positioned in front of the offside line, he may perceive an attacker, who is on the opposite side of the last defender, to the right of the last defender and raise the flag when the player is not in an offside position. Conversely, when the referee is positioned behind the offside line, he can perceive an attacker, who is running on the opposite side of the last defender, to the left of the last defender, and not raise the flag when the player is in an advanced position. At the same time, the opposite may occur if the attacker is closer to the assistant referee than the last defender ^{Oudejans et al., 2000)}.

In support of this hypothesis, evidence has been found that the assistant referee is often positioned forward of the offside line and that he commits more flag errors when the attacker is on the opposite side of the defender and more non-flag errors when he is closer to the assistant than the defender ^{(Oudejans et al., 2007}; ^{Oudejans et al., 2005}; ^{Oudejans et al., 2000)}.

The third hypothesis attributes refereeing errors to an optical illusion by which any moving object is perceived as being further forward than its real position at a given instant when a stimulus is produced (flash-lag effect). As a result of this effect, the attacker receiving the ball, normally moving towards the opponent's goal, is perceived by the assistant referee as being further forward than his true position at the time of the pass, which would explain the flag errors ^{(Baldo et al., 2002)}.

In support of this hypothesis, some studies find a bias in favor of flag-errors. However, they maintain that the occurrence of the two types of errors in different situations can only be explained by the combined effect of the second and third hypotheses ^{(Baldo et al., 2002}; ^{Helsen et al. 2006}; ^{Helsen et al., 2007)}. On the contrary, a later study finds a general bias in favor of non-flag errors that could not be explained, in the absence of other assumptions, by any of the aforementioned hypotheses ^{(Catte euw et al., 2010)}.

In addition to the three hypotheses presented above, studies have also analyzed the effect of fatigue ^{(Helsen et al., 2006}; ^{Catteeuw et al., 2010}; ^{Mallo et al., 2012)}, the speed of the assistant referee's movement ^{(Oudejans et al., 2005}; ^{Catteeuw et al., 2010)}, the distance between the last defender and the attacker ^{(Wühr et al., 2015)} and the preferences of people ^{(Wühr et al., 2020)} on errors made when judging offside.

The present paper attempts to analyze in depth the explanation given by the first hypothesis mentioned above, formalizing its approach from a mathematical point of view. In the next section, a model is developed that gathers the main elements of a typical game situation in which the assistant referee must judge a possible offside, while identifying the determinants of the difficulties he faces; in the third section, the result of a set of estimations that allow the verifying and quantifying the derivations of the model is presented; in the fourth section, the scope and implications of such derivations are discussed; and in the last section, the conclusions of the study are developed.

Therefore, the general objective of this article is to identify the determinants of the degree of difficulty for the assistant referee to correctly judge a possible offside.

MATERIALS AND METHODS

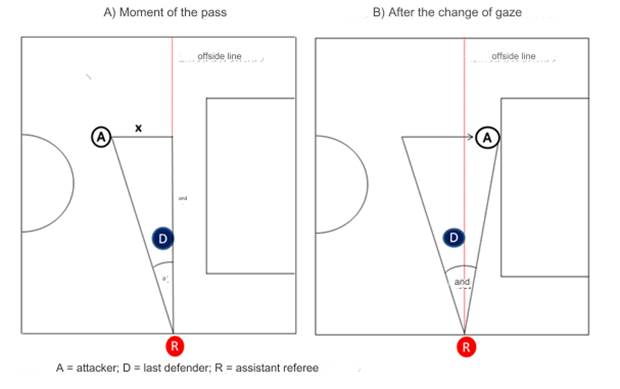
Figure 1 illustrates a typical attacking situation in which the assistant referee must judge a possible offside. At the moment of the pass (Panel A), the attacker who will receive the ball (A) is in the opponent's half, at a distance x from the offside line. The assistant referee (R) is correctly placed on the offside line, defined by the position of the last defender (D), and at a distance y from the orthogonal projection point of the attacker on the offside line (Figure 1).

Fig. 1.  - Angle between the attacker and the last defender from the assistant referee's position 

From the perspective of the assistant referee, an angle á between the position of the attacker (A) and the corresponding position of the defender (D) is displayed at the time of the pass. The magnitude of this angle can be expressed as the following Equation 1:

$\propto =arc tg \left(\frac{x}{y}\right)$ (1)

The angle á will be negative if this sign is assigned to x when the attacker is behind the offside line and will be positive otherwise. Furthermore, taking into account that the arc-tangent function is increasing throughout its path ^{(Kalnin, 1973)}, it can be shown that the angle á will be a growing function of the distance separating the attacker from the line of the offside (x) and decreasing the distance between the assistant referee and the orthogonal projection point of the attacker on the offside line (y).

Although á is the angle that makes it possible to correctly judge the possible offside, it is not the angle that the assistant referee perceives according to the hypothesis of the change of gaze. Indeed, according to this theory, the assistant referee is able to fix his gaze on the last defender and evaluate the relative position of the attacker milliseconds after the pass, when the latter has already advanced towards the opponent's goal and the angle formed between the two players has changed (Figure 1, Panel B).

In order to determine the magnitude of the change that the angle suffered, from the moment of the pass until the assistant referee is able to visualize it, it is necessary to differentiate the above function with respect to time (t), as represented in Equation 2:

$d\propto = \frac{y}{\left(x^2+y^2\right)} \frac{dx}{dt} dt$ (2)

This expression shows that the magnitude of the change in angle (dá) depends on the time it takes the assistant referee to make the change of gaze (dt), the speed with which the attacker advances (dx/ dt) and the derivative of the angle with respect to x.

The aforementioned derivative measures how much the angle varies before an advance of the attacker. From his mathematical expression (y/ (x2 + y²)) it is clear that the change of the angle depends on the position of the attacker at the time of the pass ^{(Woods & Bailey, 1944)}. On the one hand, it can be affirmed that the smaller the absolute value of the distance separating him from the offside line (|x|) the greater the variation that the angle will experience during the change of look.

On the other hand, no similar relationship can be established between the other variable that defines the initial position of the attacker (y) and the variation that the alluded angle will experience. However, considering that the assistant referee is usually further away from the play than the attacker from the offside line (y > |x|), a fairly general relationship can be established. Under this assumption, the greater the distance separating the assistant referee from the play (y) the smaller the variation of the angle during the change of gaze. This conclusion follows from the fact that the derivative of dá respect to y is negative whenever y > |x|.

RESULTS AND DISCUSSION

Table 1 presents a set of estimates that allow us to verify and, at the same time, quantify the derivations of the model developed above for a set of specific situations.

In particular, the table shows the amplitude of the angle perceived from the position of the assistant referee between the attacker and the last defender, at the time of the pass (columns 2, 5 and 8) and 250 thousandths of a second after the pass (columns 3, 6 and 9), as well as the difference between both magnitudes (columns 4, 7 and 10). The calculation is presented, on the one hand, for different distances between the attacker and the offside line at the time of the pass, which go from 5 meters behind to 5 meters in front of it (rows) and; on the other hand, for different distances between the assistant referee and the orthogonal projection of the attacker on the offside line (columns). In particular, in this case, values of 10, 35 and 60 meters were assigned to represent players advancing from the right, from the center or from the left of the field.

It was considered a time window of 250 thousandths of a second between both measurements because this is the average time that, according to specialists, it takes the assistant referee to complete the change of gaze from the player making the pass to the last defender. However, it should be noted that this time span is variable as it depends on the amplitude of the angle formed between both players ^{(Belda Maruenda, 2004}; ^{Sanabria et al., 1998)}.

For the purposes of the calculations, it was also assumed that the attacker advances towards the offside line at a speed of 7.5 meters per second, a reasonable parameter for a professional soccer player ^{(Belda Maruenda, 2004}; ^{Sanabria et al., 1998)}, while the defender remains in his position during that period of time.

Firstly, calculations show that the perceived angle, from the position of the assistant referee, between the attacker and the last defender, at the time of the pass, is an increasing function of the distance between the attacker and the offside line. For example, if the attacker runs through the center of the field and is 5 meters behind the offside line the angle will be -8.13 degrees. As the player advances, the amplitude decreases until it reaches zero and then begins to increase as the player crosses the offside line.

Secondly, it can be observed that the magnitude of the angle in absolute value decreases as the distances separating the assistant referee from the orthogonal projection of the attacker on the offside line increases. As an example, if the attacker is five meters in front of the offside line at the time of the pass and runs along the right side of the field, the angle will be 26.57 degrees. However, if he runs down the center of the field or on the left side of the field, the angle is reduced to 8.13 degrees or 4.76 degrees, as the case may be.

Third, calculations show that the difference between the perceived angle, from the assistant referee's position, between the attacker and the last defender, at the time of the pass and 250 milliseconds after the pass, is a decreasing function of the absolute vale of the distance separating the attacker from the offside line. For example, if the attacker runs down the right side and is five meters behind the offside line at the time of the pass, the angle difference will be 9.21 degrees. However, when he reaches the offside line, this difference increases to 10.62 degrees, while when he passes over it, it decreases again (Table 1).

Table 1. - Angle between the attacker and the last defender from the assistant referee's position (degrees)  

-		Distance between the assistant referee and the orthogonal projection of the attacker on the offside line
		10 meters			35 meters			60 meters
		Angle at Passing	Angle 250 m after	Difference	Angle at Passing	Angle 250 m after	Difference	Angle at the top of the pass	Angle 250 m after		Difference
Position of the attacker with respect to the offside line at the time of the pass (meters)	-5	-26.57	-17.35	9.21	-8.13	-5.10	3.03	-4.76	-2.98	1.78
	-4	-21.80	-12.00	9.80	-6.52	-3.47	3.05	-3.81	-2.03	1.79
	-3	-16.70	-6.42	10.28	-4.90	-1.84	3.06	-2.86	-1.07	1.79
	-2	-11.31	-0.72	10.59	-3.27	-0.20	3.07	-1.91	-0.12	1.79
	-1	-5.71	5.00	10.71	-1.64	1.43	3.07	-0.95	0.84	1.79
	0	0.00	10.62	10.62	0.00	3.07	3.07	0.00	1.79	1.79
	1	5.71	16.04	10.33	1.64	4.70	3.06	0.95	2.74	1.79
	2	11.31	21.18	9.87	3.27	6.32	3.05	1.91	3.70	1.79
	3	16.70	25.99	9.29	4.90	7.93	3.03	2.86	4.65	1.78
	4	21.80	30.43	8.63	6.52	9.53	3.01	3.81	5.59	1.78
	5	26.57	34.51	7.94	8.13	11.11	2.98	4.76	6.54	1.77

Finally, it can be observed that the aforementioned difference in angles is also a decreasing function of the distance separating the assistant referee and the orthogonal projection of the attacker on the offside line. For example, if the attacker is positioned on the offside line at the moment of the pass and runs down the right side, the difference in angles will be 10.62 degrees. However, if he run down the center of the field or to the left, this difference is reduced to 3.07 degrees or 1.79 degrees, respectively.

Up to this point, the various analyses carried out on the offside have focused on identifying the main causes of refereeing errors in this area, without providing a more general conceptual framework that takes into account the relative difficulty involved in judging different situations. This paper is original in that it adopts this latter approach.

The absolute value of the angle perceived from the position of the assistant referee between the attacker who will receive the pass and the last defender provides, in the absence of a change of gaze, an objective measure of the relative difficulty that the assistant faces in judging a possible offside. In this sense, both the developed model and the aforementioned estimations show that the play will be more difficult to judge the closer the attacker is to the offside line, in front of or behind it at the moment of the pass, and the farther the play is from the assistant referee, as in these cases, the perceived angle will tend to be lower in absolute value.

When the assistant referee changes perspective, from the player who throws the pass to the last defender, a distortion is introduced that makes judging the offside more difficult. As a consequence of this, the assistant referee will not perceive the aforementioned angle at the time of the pass, but a few milliseconds later, when it has already been modified. The model and the estimates presented show that this angle modification will be greater the closer the play is to the assistant referee and the closer the attacker is to the offside line at the time of the pass.

These last two derivations of the model are perhaps the most important. Indeed, up to this point, the proponents of the gaze change hypothesis have stated that errors in the offside penalty are a directly function of two factors: the speed of the attacker's movement; and the time taken for the gaze change. The model presented here shows that the distortion introduced by the change of gaze also depends on the attacker's position at the time of the pass, that is, his distance from both the assistant referee and the offside line.

In particular, it is worth noting the impact of the distance between the attacker and the offside line on the mentioned distortion. Generally, this distance is minimal as a consequence of the attacker trying to overtake the last defender in the race towards the goal, but without overtaking him at the time of the pass. Furthermore, when this distance tends to zero, the variation of the angle tends to its maximum value (Figure 2). Therefore, it can be stated that the assistant referee, in most cases, must judge the possible offside at the precise moment when the distortion derived from the change of gaze reaches its maximum expression (Figure 2).

Note: It is assumed that the attacker advances through the center of the field. Source: based on own estimates

Fig. 2.  - Variation of the angle between the attacker and the last defender during the assistant referee's change of perspective 

The hypothesis of the change of look thus acquires, with the aforementioned mathematical foundation, another level of solidity and relevance. Notwithstanding this, it should be remembered that this hypothesis can only explain those refereeing errors characterized by the raising of the flag when the attacker is enabled, but not the offsides not signaled by the assistant referee.

CONCLUSIONS

In this paper, a conceptual framework and an indicator are presented that objectively measure the difficulty the assistant referee faces in judging a possible offside. It is also demonstrated that, under the assumption that he makes a change of gaze from the player passing the ball to the last defender, the assistant referee must judge the possible offside at the moment when the distortion resulting from this change acquires its maximum expression.

REFERENCIAS BIBLIOGRÁFICAS

Baldo, M.V.C., Morya, E., & Ranvaud, R.D. (2002). Flag Errors in Soccer Games: The Flash-Lag Effect Brought to Real Life. Perception, 31, 1205-1210. http://fisio2.icb.usp.br:4888/~vinicius/publications/Baldo_Ranvaud_Morya%202002%20.pdf

Belda Maruenda, F. (2004). Can the human eye detect an offside position during a football match? British Medical Journal, 329, 1470-1472. https://www.bmj.com/content/329/7480/1470

Carosi, J. (2010). The history of offside. http://www.kenaston.org/download/KenAstonRefereeSociety/offside_history-JulianCarosi.pdf

Catteeuw, P., Gilis, B., Helsen, W., & Wagemans, J. (2010). Offside decision making of assistant referees in the English Premier League: Impact of physical and perceptual-cognitive factors on match performance. Journal of Sports Sciences, 28(5), 471-481. https://www.researchgate.net/publication/43343901_Offside_decision_making_of_assistant_referees_in_the_English_Premier_League_Impact_of_physical_and_perceptual -cognitive_factors_on_match_performance

Clark, R. (2016). Revising FIFA´s Laws of the Game. Law Student Papers, Duquesne University. https://dsc.duq.edu/law-student-papers/7/

Helsen, W., Gilis, B., & Weston, M. (2007). Helsen, Gilis, and Weston (2006) do not err in questioning the optical error hypothesis as the only major account for explaining offside decision-making errors. Journal of Sports Sciences , 25(9), 991-994. https://www.researchgate.net/publication/6335394_Helsen_Gilis_and_Weston_2006_do_not_err_in_questioning_the_optical_error_hypothesis_as_the_only_major_account_for_explaining_offside_decision -making_errors

Helsen, W., Gilis, B., & Weston, M. (2006). Errors in judging "offside" in association football: Test of the optical error versus the perceptual flash-lag hypothesis. Journal of Sports Sciences , 24(5), 5211-528. https://www.researchgate.net/publication/7170934_Errors_in_judging_offside_in_association_football_Test_of_the_optical_error_versus_the_perceptual_flash -lag_hypothesis

Hüttermann, S., Noël, B. & Memmert, D. (2017). Evaluating erroneous offside calls in soccer. Plos One, 12(3). https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0174358

International Football Association Board (2023). Reglas de Juego 23/24. IFAB. https://www.theifab.com/documents/?documentType=all&language=en&years=2023

International Football Association Board (2018). Circular No 12. Important information about Video Assistant Referees (VAR). IFAB. https://downloads.theifab.com/downloads/circular-12_en?l=en

Kalnin, R.A. (1973). Álgebra y funciones elementales. Mir. https://elsolucionario.net/algebra-funciones-elementales-r-kalnin-1ra-edicion/

Mallo, J., Gonzalez Frutos, P., Juárez, D., & Navarro, E. (2012). Effect of positioning on the accuracy of decision making of association football top-class referees and assistant referees during competitive matches. Journal of Sports Sciences , 30(13), 1437-1445. https://core.ac.uk/download/pdf/148664622.pdf

Oudejans, R.R., Bakker, F.C., & Beek, P. J. (2007). Helsen, Gilis and Weston (2006) err in testing the optical error hypothesis. Journal of Sports Sciences , 25(9), 987-990. https://www.researchgate.net/publication/6335393_Helsen_Gilis_and_Weston_2006_err_in_testing_the_optical_error_hypothesis

Oudejans, R.R., Bakker, F.C., Verheijen, R., Gerrits, J.C., Steinbrückner, M., & Beek, P. J. (2005). How position and motion of expert assistant referees in soccer relate to the quality of their offside judgements during actual match play. International of Sport Psychology, 36, 3-21. https://www.researchgate.net/publication/232596432_How_position_and_motion_of_expert_assistant_referees_in_soccer_relate_to_the_quality_of_their_offside_judgements_during_actual_match

Oudejans, R.R., Verheijen, R., Bakker, F.C., Gerrits, J.C., Steinbrückner, M., & Beek, P. J. (2000). Errors in judging `offside' in football. Nature, 404(6773):33. https://www.researchgate.net/publication/12600290_Errors_in_judging_'offside'_in_football

Sanabria, J., Cenjor, C., Márquez, F., Gutiérrez, R., Martinez, D., & Prados-García, J.L. (1998). Oculomotor movements and football's Law 11. The Lancet, 351, 268. https://www.thelancet.com/journals/lancet/article/PIIS0140-6736(05)78269-6/abstract

Woods, F. S., & Bailey, F. H. (1944). Analytic geometry and calculus. Athenaeum Press.

Wühr, P., Fasold, F., & Memmert, D. (2020). The impact of team preferences on soccer offside judgments in laypersons: a quasi-experimental study.Cognitive Research: Principles and Implications, 5, 1-24. https://cognitiveresearchjournal.springeropen.com/articles/10.1186/s41235-020-00253 -2

Wühr, P., Fasold, F., & Memmert, D. (2015). Soccer Offside Judgments in Laypersons with Different Types of Static Displays. Plos One , 10(8). https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0133687

Received: December 05, 2023; Accepted: March 20, 2024

^*Autor para la correspondencia: [e-mail]

Los autores declaran no tener conflictos de intereses.

Todos los autores han participado de forma activa en la redacción del trabajo y análisis de los documentos.