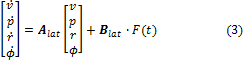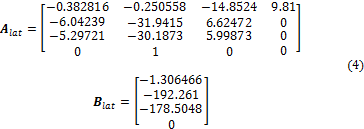ARTÍCULO ORIGINAL

 

 

Estudio sobre la estrategia de guiado L1 para el seguimiento de caminos rectos y curvos en UAV

 

Study on the L1 guiding strategy for the tracking of straight and curved paths in UAV

 

 

Luís Hernández-Morales, Yunier Valeriano-Medina, Anailys Hernández-Julián, Luís Hernández-Santana.

Universidad Central de Las Villas (UCLV), Cuba.

 

 

---

RESUMEN

El desarrollo de los vehículos autónomos es un tema de gran interés en la comunidad científica internacional. Para el cumplimiento de misiones sin intervención humana es de vital importancia contar con un algoritmo o ley de guiado. En este trabajo se presentan los resultados obtenidos mediante simulaciones con el algoritmo de guiado basado en la distancia L1, durante el seguimiento de caminos rectos y circulares por parte de un vehículo aéreo no tripulado (UAV, por sus siglas en inglés). El algoritmo produce un mando de aceleración lateral que es interpretado por el controlador de balanceo para lograr la convergencia al camino. Los resultados de la simulación demuestran las buenas prestaciones del algoritmo, tanto para caminos rectos como en caminos circulares.

Palabras claves: UAV, guiado, distancia L1.

---

ABSTRACT

The development of autonomous vehicles is a subject of great interest in the international scientific community. For the accomplishment of missions without human intervention it is vitally to have an algorithm or guiding law. In this paper we present the results obtained by simulation with the guidance algorithm based on distance L1, during the tracking of straight and circular paths by an autonomous aerial vehicle (UAV). The algorithm produces a lateral acceleration command that is interpreted by the balancing controller to achieve convergence to the path. The results of the simulation demonstrate the good performance of the algorithm, for both straight and circular paths.

Key words: UAV, guidance, distance L1.

---

 

 

1.- INTRODUCCIÓN

 

Un UAV es un vehículo autónomo aéreo capaz de operar y realizar maniobras sin requerir la guía de un piloto o de un teleoperador [1]. Estos vehículos están siendo cada vez más utilizados en diferentes aplicaciones, tales como: militares, de investigación e industriales.  En Cuba, el Grupo de Automatización, Robótica y Percepción (GARP), perteneciente a la Universidad Central ¨Marta Abreu¨ de Las Villas, trabaja desde hace algunos años con vehículos de este tipo, logrando relevantes resultados en las áreas del modelado y el control [2]. Sin embargo, para las aplicaciones relacionadas con la agricultura de precisión que actualmente son de interés para GARP [3], resulta de vital importancia el estudio de los esquemas de guiados que aseguran el cumplimiento de misiones de seguimiento por parte de la aeronave. Especialmente, interesa el algoritmo basado en la distancia L1 [4-6], ya que el mismo se encuentra implementado en el hardware Arduino que constituye la tecnología utilizada por GARP en sus aviones.

El guiado representa la metodología básica que define el comportamiento del movimiento transitorio de los vehículos, con la intención de lograr el control sobre el movimiento en el seguimiento de caminos [7]. Su función consiste en proporcionar de forma continua al controlador el estado de las referencias necesarias (posición, velocidad y aceleración) para que el vehículo recorra la ruta de manera precisa. Existen distintos escenarios de control que se encuentran asociados a los objetivos de control que se desean para la aplicación. Entre estos se encuentra el de seguimiento de un camino sin considerar restricciones temporales [4]. Los algoritmos de guiado son los encargados de calcular los valores deseados de los lazos de control de balanceo, velocidad de avance, rumbo o altura que son los encargados de actuar sobre el vehículo.

En la actualidad se utiliza un gran número de algoritmos para el seguimiento de caminos, todos basados en algunas de las estrategias siguientes: Línea de Visión (LOS, Line of Sight), Persecución (PP, Pure Pursuit) y Dirección Constante (CB, Constant Bearing) [7]. En trabajos anteriores, GARP ha evaluado el desempeño de un algoritmo conocido como I-LOS para el caso del seguimiento de caminos rectos por parte del vehículo subacuático HRC-AUV [8]. La principal característica de este esquema es que contiene una acción integral en la ley de guiado que permite reducir los errores de seguimiento que se producen debido a las perturbaciones marinas.

El algoritmo basado en la distancia L1 fundamentalmente se emplea en vehículos aéreos [4,5]. Ha demostrado un desempeño satisfactorio durante el seguimiento de caminos rectos y circulares. Su ajuste es sencillo, pues sólo se necesita determinar dos parámetros. En este trabajo se ajusta el algoritmo y se evalúa su desempeño durante el seguimiento de caminos rectos y circulares. Para ello se utiliza el UAV Skywalker x8, cuyas características físicas son similares a las de los UAV con los cuales trabaja GARP, y su modelo dinámico se encuentra disponible en [9]. En la investigación no se ha tenido en cuenta los efectos que provoca el viento.

En el presente artículo se presenta el modelo del subsistema lateral del UAV Skywalker x8, para luego definir las ecuaciones que definen el algoritmo L1 tanto para caminos rectos como circulares, y por último se presentan los resultados de simulación del algoritmo durante el seguimiento de ambos caminos.

 

2.- Modelo del UAV Skywalker x8

 

Disponer del modelo dinámico de la aeronave permitirá realizar la síntesis y sintonía de los lazos de control y es necesario para el trabajo de simulación. Las maniobras de los vehículos aéreos abarcan los movimientos en los seis grados de libertad (6 GDL). Los grados de libertad están determinados por los desplazamientos independientes y rotaciones que especifican totalmente la posición y orientación del vehículo [10]. Las tres primeras coordenadas y sus derivadas en el tiempo se emplean para describir la posición y el movimiento lineal del vehículo a lo largo de los ejes x, y y z, mientras que las tres coordenadas restantes se utilizan en la representación de la orientación y el movimiento rotatorio (Figura 1).

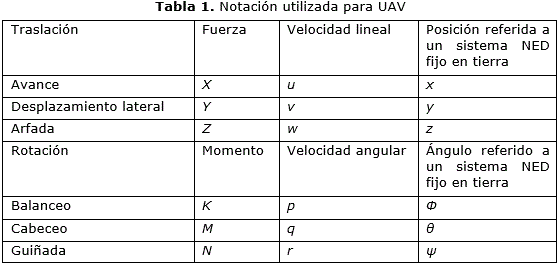
La Tabla 1 resume la nomenclatura estándar empleada para describir el movimiento de vehículos.

Las ecuaciones que describen el movimiento de un vehículo aéreo en el espacio tridimensional pueden obtenerse a partir de las leyes de conservación de los momentos lineales y angulares referidos a un sistema inercial de referencia. En Mathematical models for control aircraft and satellites [11], se demuestra que la segunda ley de Newton puede expresarse para cualquier vehículo aéreo con un sistema de coordenadas fijo al cuerpo referido a un sistema de referencia inercial North, East, Down (NED) según la Figura 1, de la siguiente manera:

donde M_RB es la matriz de cuerpo rígido, N_RB es la matriz de Coriolis del cuerpo rígido, g(η) es el vector de las fuerzas gravitacionales y τ es un vector generalizado que incluye las fuerzas aerodinámicas y de control [11]. En la ecuación (1), v=[u, v, w, p, q, r]^T representa al vector de velocidad del vehículo, mientras que η=[x, y, z, f, θ, ψ]^T es el vector de posición y orientación.

2.1- Modelo para el subsistema lateral

En el modelado de aviones es común suponer que el sistema longitudinal está desacoplado del subsistema lateral. El desacople se justifica debido a que se considera que el fuselaje es delgado, y que la longitud del avión es mucho más grande que su ancho y altura. Otra consideración a tener en cuenta es que la velocidad longitudinal es mucho más grande que la lateral y la vertical. Los subsistemas en los que se divide el modelo de 6 GDL del avión y sus variables de estado son:

       •  Subsistema longitudinal: empleado para el control de altura y compuesto por los estados u, w, q, θ y ψ.

       •  Subsistema lateral: utilizado para las maniobras de dirección del vehículo y compuesto por los estados v, p, r y f. Como el objetivo de este trabajo es el guiado, solamente presentaremos el modelo de este subsistema.

El modelo no lineal puede ser linealizado a partir de un punto de operación y pequeñas variaciones a su alrededor. En el modelado de aeronaves el punto de operación se define a partir de considerar un valor de velocidad constante. La ecuación del modelo lineal tiene la siguiente forma:

La tarea más compleja en esta dirección es encontrar las fuerzas y momentos aerodinámicos [12]. En [13, 14] se obtiene un modelo no lineal para la aeronave UAV Skywalker x8 utilizando métodos computacionales. La estructura lineal para el subsistema lateral tiene la forma:

Donde F(t) es el ángulo de alerón δa que constituye la señal de mando del sistema lateral.

Las matrices A_lat y B_lat del modelo lateral del UAV Skywalker x8 se obtienen del apéndice E del trabajo [9] y poseen los siguientes valores numéricos:

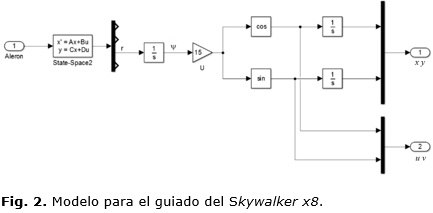
No obstante, el modelo (ecuación (4)) no proporciona información sobre la posición del vehículo, que es necesaria para el guiado. Esta información se puede obtener integrando el estado r para obtener la guiñada ψ, que operada trigonométricamente con el módulo de la velocidad U y el punto de operación, nos da la velocidad en cada eje referida al sistema fijo en tierra. Las integrales de dichas velocidades nos proporcionan la posición en x y y. El diagrama de bloques de la Figura 2 muestra el modelo para el guiado. Debe destacarse que este modelo general vuelve a ser no lineal y su eventual linealización implicaría fijar un punto de operación en la guiñada ψ_o.

 

3.- Algoritmo de Guiado L1

 

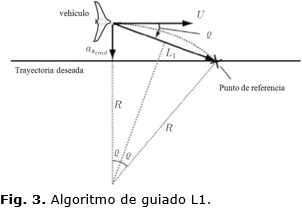
El algoritmo de guiado basado en la distancia L1 permite el seguimiento de trayectorias rectas y curvas. La teoría asociada al método plantea que se debe escoger un punto de referencia en la trayectoria deseada, a partir del cual se calculará un mando de aceleración lateral para que el vehículo se dirija hacia el camino [5, 15]. El punto de referencia se considera ubicado en la trayectoria deseada a una distancia L₁ desde el vehículo, tal como se muestra en la Figura 3.

La aceleración lateral obliga al vehículo a desplazarse hacia la línea de la trayectoria deseada. Su valor debe disminuir en la medida en que la separación entre el vehículo y el trayecto sea menor. Cuando el vehículo esté sobre la trayectoria la aceleración lateral demandada por el mismo será cero. Esta acción de mando obliga a que el vehículo se desplace por el trayecto deseado.

En la Tabla 2 se presentan las variables que intervienen en el algoritmo:

La aceleración lateral no es más que la aceleración centrípeta necesaria para seguir el camino circular de radio R definido por la posición del punto de referencia, la posición del vehículo y el vector de velocidad del vehículo, tal como se muestra en la Figura 3. En este sentido la aceleración centrípeta se define como:

Como se aprecia en la Figura 3 existe una relación entre la distancia L₁ y R la cual sustituyéndola en la ecuación (5) se llega a la expresión del comando de aceleración lateral, el cual está determinado por:

De la ecuación (6) cabe destacar que la dirección de la aceleración depende del signo del ángulo entre la distancia L1 y U. Además, es importante señalar que cuando el vehículo esté alejado del camino, el ángulo ϱ será de mayor amplitud, por lo que la aceleración tendrá un valor elevado, pero cuando el vehículo se encuentre sobre la línea del camino este ángulo tendrá valor cero por lo que no existirá aceleración lateral, siendo así como el algoritmo consigue converger a la trayectoria deseada.

Sin embargo, la variable aceleración lateral no corresponde a ninguno de los estados del modelo del vehículo. Es por eso que la aceleración lateral debe ser asociada con alguno de dichos estados. Para ello se propone la ecuación (7) [6] que relaciona el balanceo deseado con la aceleración lateral demandada por el algoritmo de guiado L1:

Este valor de balanceo deseado constituye la referencia proporcionada por el algoritmo L1 al lazo interno de control de balanceo.

3.1.- Linealización del algoritmo

Cuando el vehículo no está alejado de la trayectoria el valor del ángulo ϱ es pequeño, a pequeñas variaciones del mismo se puede utilizar la siguiente aproximación lineal:

A partir de relaciones trigonométricas, las cuales son descritas en [5], se llega a la expresión linealizada del algoritmo, la cual queda determinada:

Por tanto, la linealización del algoritmo hace que el control a pequeñas variaciones alrededor del punto de operación se comporte como un controlador PD que actúa sobre el error perpendicular al camino. Además, como se puede apreciar en la ecuación (9), las ganancias proporcional y derivativa del controlador dependen del valor del módulo de la velocidad del vehículo (U) y de la distancia L₁.

3.2.- Evaluación del algoritmo en caminos rectos

Para la evaluación del algoritmo en caminos rectos se toma como base la implementación del mismo que se encuentra en el firmware de Arduino [15]. A través del software de supervisión Mission Planner se define una serie de puntos de camino (Wp) entre los cuales el software traza una serie de tramos rectos que el vehículo debe seguir. Para hallar el valor de aceleración lateral es preciso conocer los valores de U, L1 y ϱ, para lo cual se aplica la siguiente solución:

La magnitud de U es determinada como:

La distancia L₁ se calcula a partir de dos parámetros ajustables por el operador φ y T que brinda el código. Estos parámetros representan un coeficiente de amortiguamiento y un periodo respectivamente, y a partir de los mismos el firmware de Arduino brinda la siguiente ecuación para el cálculo de la distancia L₁ [15]:

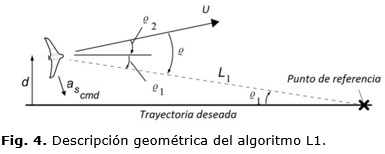
El ángulo ϱ es el que se forma entre la distancia L₁ y U, y de acuerdo con la Figura 4 se puede calcular para cualquier valor del mismo como:

Donde ϱ₁ se puede definir geométricamente de la siguiente forma:

Por su parte d se determina como:

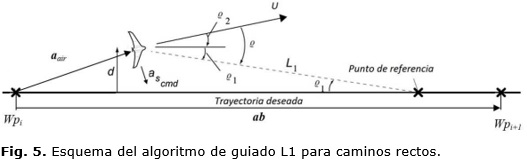
Donde de acuerdo con la Figura 5:

       •  ab es la magnitud de la proyección del vector formado por el punto vencido (Wpi) y el punto a vencer (Wpi +1).

       •  representa el vector ab normalizado.

       •  a_air es el vector formado por el punto vencido (Wpi) y la posición actual del avión (Pxy).

Mientras que ϱ₂ se halla de la siguiente forma:

De esta manera se cuenta con todos los términos necesarios para calcular la aceleración lateral de acuerdo con la ecuación (6).

3.3.- Seguimiento de trayectorias circulares

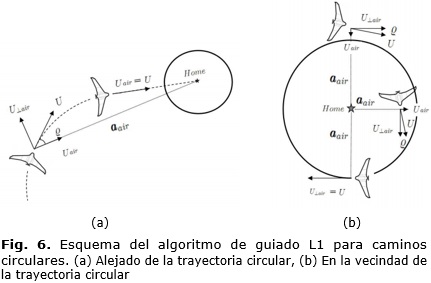
Para la evaluación del algoritmo en caminos circulares se toma como base una vez más la implementación que se encuentra en el firmware de Arduino [15]. A través del software de supervisión Mission Planner se establece un punto denominado Home, al cual el vehículo se dirige al finalizar una misión o cuando pierde la comunicación con la estación en tierra. Este punto constituye el centro de un círculo que debe ser definido previamente por el usuario. En este tipo de misiones se pueden apreciar dos escenarios: cuando el vehículo se encuentra alejado de la trayectoria circular a seguir (Figura 6(a)) y cuando se encuentra en la vecindad de la misma (Figura 6(b)).

En la Tabla 3 se presentan las variables que intervienen en el algoritmo:

Para el caso en que el vehículo se encuentre alejado de la trayectoria deseada, el propósito debe ser que se acerque al círculo, por lo que la aceleración lateral debe calcularse a través de la ecuación (6). Los componentes de la misma se calculan de igual manera que en el caso de caminos rectos con la excepción del ángulo ϱ, el cual se calcula de la siguiente forma:

Ya una vez que el vehículo se encuentra en la vecindad de la trayectoria deseada pasará a seguir una trayectoria circular, para lo cual resulta necesario aplicarle una componente de aceleración centrípeta nominal (a_cen) y otra componente de aceleración (a_cir). Esta última es la encargada de hacer cero el error de seguimiento perpendicular al camino. Por tanto, la aceleración lateral queda definida de la siguiente forma:

Por su parte la aceleración a_cen se expresa como:

El denominador de la ecuación expresada anteriormente representa una medida de protección implementada en el código de Arduino donde se escoge el mayor valor entre los términos R/2 y R + d.

La a_cir se calcula a partir de la expresión linealizada del algoritmo (ecuación (9)), quedando definida a partir de d y U_air de la siguiente forma:

Kx y Kv son las constantes del controlador y son calculadas en función de φ y T tal como quedó expresado anteriormente. Las constantes del regulador son definidas en la implementación del código como [15]:

De esta manera resulta posible calcular mediante el algoritmo basado en la distancia L1 la señal de aceleración lateral para cuando el vehículo siga caminos circulares.

 

4.- Evaluación del algoritmo de guiado L1 mediante simulación

 

Para implementar un sistema de control de movimiento que incorpore la capacidad de cumplir misiones de manera autónoma en un vehículo aéreo, se hace necesario contar con varios bloques funcionales como se muestra en la Figura 7. Tal como se ha expresado con anterioridad, el objetivo de esta investigación es evaluar un esquema de guiado basado en el parámetro L1 para el UAV Skywalker x8. El bloque de guiado tendrá como salida el mando de aceleración lateral calculado por el algoritmo basado en la distancia L1, el cual resulta esencial para lograr la convergencia de la posición del vehículo a un camino predefinido.

4.1- Controlador de balanceo para el UAV

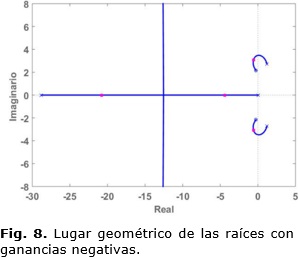
Acorde a la ecuación (7) el sistema de guiado demanda de la solución de un lazo interno de control de balanceo. Para la síntesis de este controlador se parte del modelo linealizado del subsistema lateral (ecuación (4)). La señal de mando del sistema es la deflexión angular de los alerones δ_a, como señales de realimentación para el control demandado se dispone de la medición directa del balanceo f y de la variación de balanceo p. La mayoría de los autores sugieren como estrategias de control de los lazos de balanceo variantes de reguladores PID [12], [15]. En esa línea una alternativa factible es la implementación de controladores P o P-D. Ambas estrategias fueron evaluadas, no obstante, la estrategia P-D no reporta mejoras con relación a la P, sobre esa base y atendiendo a la mayor simplicidad se adoptó la estrategia P como la estrategia para el control de balanceo. Se muestra el análisis en el lugar geométrico de las raíces (LGR), tomando como base la relación δ_a vs f del modelo de espacio estado (ecuación (4)). Este sistema se hace inestable ante valores positivos de ganancia por lo que se dispone diseñar el sistema con ganancias negativas como se muestra en la Figura 8.

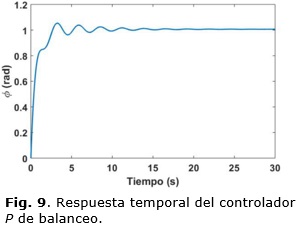
Por lo que queda un controlador P con valor de ganancia igual a -2. La respuesta temporal del sistema queda expresada en la Figura 9. El tiempo de subida de alrededor de 3 segundos es perfectamente compatible con las exigencias de guiado demandadas por la aplicación. Esta solución de control ofrece un margen de fase de más de 50^o y un margen de ganancia de 7dB, lo que garantiza una robustez razonable para la solución propuesta, sobre todo si se tiene en cuenta que es un lazo interno de una cascada. Diseños optimizados con soluciones de tipo PID ofrecen mejores respuestas, pero demandan valores de ganancia muy altos, de escaso valor práctico pues saturarían el mando rápidamente en cualquier aplicación. 

4.2- Aplicación de L1 en UAV Skywalker x8

Una vez ajustado el lazo interno de control se procede a sintonizar el lazo completo de guiado. El ajuste del algoritmo L1 se realiza teniendo en cuenta las condiciones de operación de la aeronave Skywalker x8. La velocidad de operación de este avión es de U=15 m/s.

Si bien en la ecuación (9) se logra representar en una aproximación lineal el algoritmo L1, el comportamiento del mismo y el modelo son fuertemente no lineales, haciendo muy complejo el uso de los métodos clásicos para la sintonía del sistema. Ello sugiere el uso de la simulación como herramienta para seleccionar los parámetros ajustables del mismo. Un voluminoso trabajo de simulación fue realizado haciendo variaciones a los parámetros ajustables. Son sintonizados los parámetros T y φ en 25 y 0.75 respectivamente, valores que coinciden con los recomendados por parte de Ardupilot [15].

En la Tabla 4 se presentan los puntos correspondientes a un camino recto.

En la Figura 10(a) se presenta el seguimiento de trayectoria deseada realizado mediante simulación para este ajuste. En dicha gráfica se puede apreciar como el avión debe realizar varios giros y como es capaz de converger rápidamente al camino. En base a los puntos deseados y a la posición instantánea del vehículo se determina el error de seguimiento perpendicular al camino. En la Figura 10(b) se presenta el comportamiento de este error, tal como se puede apreciar, se logra reducir el error de seguimiento perpendicular al camino e incluso en varios momentos llega a estabilizarse en cero, demostrándose que el vehículo converge al camino.

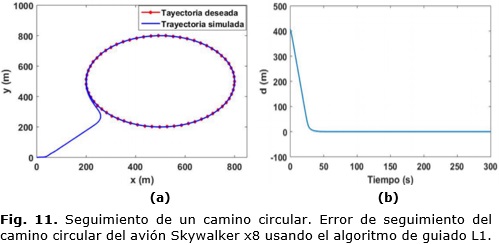
Para el caso de los caminos circulares, se considera como trayectoria deseada un círculo de radio 300 m y centro en el punto (500, 500). En la Figura 11(a) se puede apreciar como el avión sale de un punto inicial (0,0) y se dirige al centro, ya una vez en la vecindad de la trayectoria, converge al camino con rapidez siguiendo posteriormente la trayectoria deseada. En la Figura 11(b) se presenta el comportamiento del error de seguimiento del camino, tal como se puede apreciar, se logra reducir este error hasta un valor casi cero.

4.3- Análisis de perturbaciones

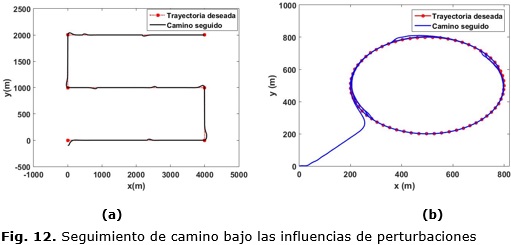
En otros trabajos se evidencia por las simulaciones presentadas que el algoritmo es robusto ante perturbaciones de viento constantes [5], [6], En esta dirección se dispone a realizar un análisis mediante simulación de cómo se comporta el algoritmo ante perturbaciones. Para la simulación se toma una perturbación tipo paso que varía cada cierto tiempo a través del eje y. En la Figura 12 se aprecia el seguimiento del camino con la influencia de las perturbaciones tanto en camino rectos como en caminos circulares, en esta figura se puede apreciar que el algoritmo rechaza las perturbaciones convergiendo al camino rápidamente:

 

5.- CONCLUSIONES

 

En esta investigación se presenta el diseño del algoritmo de guiado basado en la distancia L1, con el cual se logra el seguimiento de caminos rectos y circulares por parte de un vehículo aéreo tipo UAV. El procedimiento de ajuste resulta sencillo y depende sólo de establecer los valores de dos parámetros. Para ello se toma como referencia el modelo del UAV Skywalker x8. Las pruebas realizadas demuestran que se consigue la convergencia de la aeronave a caminos rectos y circulares. Los resultados de simulación obtenidos avalan la utilización de este algoritmo como parte del sistema de control de movimiento de las aeronaves con las que trabaja GARP.

 

REFERENCIAS

 

1.       Hagen I. Autopilot Design for Unmanned Aerial Vehicles. Tesis de Maestría. NTNU; 2012. Disponible en: https://daim.idi.ntnu.no/masteroppgaver/007/7001/masteroppgave.pdf.

2.       Martinez-Jimenez BL, et al. Identificación de un vehículo aéreo no tripulado. Revista de Ingeniería Electrónica, Automática y Comunicaciones. 2012; 33(1):45-55

3.       Hernández-Santana L, et al. Levantamiento fotogramétrico de la UBPC "Desembarco del Granma" utilizando aviones no tripulados, solución de bajo costo para la agricultura nacional. VII Edición de la Conferencia Científica Internacional sobre Desarrollo Agropecuario y Sostenibilidad. AGROCENTO 2016. 8 de Abril 2016; Universidad Central "Marta Abreu" de Las Villas; Santa Clara; Cuba. ISBN: 978-959-312-174-3.

4.       Sujit PB, Saripalli S, Sousa JB. Unmanned aerial vehicle path following: A survey and analysis of algorithms for fixed-wing unmanned aerial vehicles. IEEE Control Systems.2014; 34(1): 42–59

5.       Park S, Deyst J, How JP.  Performance and lyapunov stability of a nonlinear path-following guidance method. J. Guidance, Control, Dyn. 2007; 30(6): 1718–1728.

6.       Curry R, Lizarraga M, Mairs B, Elkaim GH. L2, an improved line of sight guidance law for uavs. In: American Control Conference (ACC). IEEE. Washington DC; EE.UU.; 2013. p. 1–6.

7.       Breivik M, Fossen TI. Guidance Laws for Autonomous Underwater Vehicles. In: Inzartsev AV, editor. Underwater vehicles. Vienna, Austria: InTech; 2008. p. 51–76

8.       Valeriano-Medina Y, Hernández A, Hernández L. Controlador ilos para el seguimiento de caminos en línea recta de un vehículo autónomo subacuático. Revista de Ingeniería Electrónica, Automática y Comunicaciones. 2015; 36(2): 15 – 28.

9.       Gryte K. High Angle of Attack Landing of an Unmanned Aerial Vehicle. Tesis doctoral. NTNU; 2015 Disponible en: https://brage.bibsys.no/xmlui/handle/11250/2352405.

10.    Fossen TI.  Handbook of Marine Craft Hydrodynamics and Motion Control. Nueva York, Estados Unidos: John Wiley & Sons; 2011.

11.    Fossen TI. Mathematical models for control of aircraft and satellites, 3^rd edition. Notas de clase del curso TTK4109 Guidance and Control of vehicles. Department of Engineering Cybernetics, NTNU. Noruega; 2013. Disponible en: https://pdfs.semanticscholar.org/f1e8/9fe8c65328fde9cfff8d523f0d0db64e1ef3.pdf.

12.    Pamadi BN. Performance, Stability, Dynamics, and Control of Airplanes. Estados Unidos: American Institute of Aeronautics and Astronautics: 2003.

13.    Mathisen SH, Fossen TI, Johansen TA. Non-linear model predictive control for guidance of a fixed-wing uav in precision deep stall landing. In: 2015 International Conference on Unmanned Aircraft Systems (ICUAS). Denver, Estados Unidos; 2015. p. 356–365.

14.    Mathisen SH, Gryte K, Fossen TI, Johansen TA. Non-linear model predictive control for longitudinal and lateral guidance of a small fixed-wing uav in precision deep stall landing. In: AIAA Infotech@ Aerospace. AIAA. California, Estados Unidos; 2016

15.    ARDUPILOT. Developer/apm open source autopilot. Disponible en: http://dev.ardupilot.com/. Último acceso: 30 de enero de 2016; 2016.

 

 

Recibido: 31 de enero del 2017
Aprobado: 9 de junio del 2017

 

 

Luís Hernández Morales, Universidad Central de Las Villas (UCLV), Cuba. Correo electrónico: [e-mail].