Serviços customizados
Espanhol (pdf)
Artigo em XML
Referências do artigo
Enviar este artigo por email
Citado por SciELO 
Similares em
SciELO 
Permalink
INTRODUCCIÓN
La combinatoria estudia las posibles agrupaciones de objetos, aspecto que resulta esencial para las ciencias informáticas. Mediante la combinatoria “...los estudiantes aprenden a organizar formas exactas de conteo que los llevan a dar soluciones menos complejas, y que requieran de un menor número de recursos a problemas de cualquier índole en el sector de la economía donde se desarrollen profesionalmente” (Estopiñán M, 2017, p. 25).
Con el fin de contribuir a desarrollar el razonamiento combinatorio de los estudiantes, en el volumen I del libro Matemática Discreta de Jhonsonbaugh (2005), se ofrece un resumen de la técnica de solución de problemas que incluye: “Sustituir el problema por un problema más sencillo, lo que puede lograrse reduciendo el tamaño del problema original; Numerar los elementos de manera sistemática para que surjan patrones; Buscar patrones; Buscar un problema similar e imitar su solución” (p. 229). Vale aclarar que este libro constituye el texto básico para la impartición de la Matemática Discreta en las carreras de Ingeniería Informática e Ingeniería en Ciencias Informáticas.
En tal sentido, desde el año 1989 el consejo nacional de profesores de matemática de Estados Unidos (NTCM en Inglés) declaró que “el razonamiento combinatorio es una herramienta útil en los esquemas cognitivos de los estudiantes puesto que es la base de la matemática discreta” (Godino J. B., 2016, p. 8). Por su parte “las guías de acreditación de la Association for Computing Machinery (ACM) y del Institute of Electrical and Electronics Engineers (IEEE) hacen obligatorio un curso de matemáticas discretas que incluya entre otros temas a la combinatoria” (Johnsonbaugh, 2005, p. 15).
Auxiliándose de la combinatoria el ingeniero informático puede realizar los “... procesos de análisis de algoritmos y de programas de computadora” (Kolman, 1996, p. 72), así como realizar la búsqueda de solución de problemas especialmente cuando al realizar el modelado y reevaluar los resultados emplea “...las técnicas de la teoría de decisiones mediante la combinación de sus juicios de probabilidad y utilidad para elegir el curso de acción que le ofrezca la mayor posibilidad de éxito” (Estopiñán M, 2017, p. 25).
Diferentes fuentes bibliográficas utilizadas en la impartición de la combinatoria dentro de la matemática discreta coinciden en incluir los siguientes contenidos: Principios de la multiplicación, la suma y de las casillas; Permutaciones, r-permutaciones y combinaciones; Así como las permutaciones y combinaciones generalizadas, teorema del binomio y triángulo de Pascal. Didácticamente es necesario que el estudiante aprenda resolviendo los diferentes problemas combinatorios. (Johnsonbaugh, 2005), (Rosen, 2012), (Grimaldi, 2004), (Bogart, 2002), (Kolman, 1996), (Nieto, 1996), (Hernandez, 2018).
En relación al concepto problema, se asume la definición de Mazario (2009, p. 13): “Situación o dificultad prevista o espontánea con algunos elementos desconocidos por el sujeto, pero capaz de provocar la realización de acciones sucesivas para darle solución”.
Se está de acuerdo con que “La resolución de problemas se considera una habilidad, y como tal se caracteriza y estructura posteriormente, todo ello en base a determinadas acciones, que son las que permiten acceder a las vías para resolver problemas”, y que la habilidad para resolver problemas es “el proceso que implica la realización de una secuencia de acciones para la obtención de una respuesta adecuada a una dificultad con la intención de resolverla, es decir la satisfacción de las exigencias (meta, objetivo) que conducen a la solución del problema matemático” (Mazario, 2009, p. 13).
Varios reportes reflejan las dificultades que enfrentan los estudiantes cuando resuelven problemas combinatorios; Lockwood (2013), Lockwood (2014), Godino (2016), Mneimneh (2017) y Meika D. (2018) en cuanto a los procesos para interpretar textos, identificar y representar lo dado y lo buscado; modelar situaciones, y aplicar los contenidos teóricos de la combinatoria relacionados con el insuficiente desarrollo de la habilidad general resolver problemas de combinatoria.
Batanero et al (1997) afirma que los estudiantes de nivel preuniversitario que resuelven problemas combinatorios cometen errores con la enumeración no sistemática de casos lo que provoca la ocurrencia de omisiones, uso incorrecto de diagramas de árboles, errores de orden al confundir r-permutación con combinación y viceversa; confusión con los tipos de objetos a contar o con las caracteristicas de los subconjuntos (o de tuplas) en los modelos de partición, distribución o partición (pp. 301-304).
En la enseñanza de la combinatoria en las carreras de ciencias informáticas y carreras afines, los estudiantes repiten esos mismos errores cuya presencia pudiera estar influenciada por los métodos de enseñanza, y las formas de organización utilizadas en un contenido que se caracteriza por la forma de los problemas de conteo: “fáciles de enunciar, pero pueden tener soluciones con una complejidad subyacente. Tanto en la secundaria como en la universidad, los estudiantes son introducidos al conteo mediante fórmulas y problemas tipo, lo que puede ser beneficioso para el estudiante, pero también puede ser una desventaja ya que el estudiante puede comenzar a confiar en la memorización” (Gordon, 2019 pág. 8).
En el plan de estudio E, de la carrera Ingeniería en Ciencias Informáticas, se define a la Creatividad como uno de los valores esenciales del profesional graduado que se expresa a través de varios modos de actuación, siendo el primero la capacidad para “resolver problemas mediante la aplicación de las técnicas propias de las ciencias informáticas” (MES. Cuba, 2019, p.10); De esa manera, el desarrollo de la habilidad para resolver problemas constituye un objetivo común de todas las disciplinas de dicho plan.
En las carreras de Ingeniería Informática e Ingeniería en Ciencias Informáticas la combinatoria forma parte de la asignatura matemática discreta (en el caso de la UCI la combinatoria se incluye en la asignatura matemática discreta II), que pertenecen al departamento de Inteligencia Computacional, y se imparten en uno de los dos primeros semestres de la carrera, al inicio del ciclo básico de formación, etapa en la que los estudiantes aún presentan carencias en el desarrollo de la habilidad resolver problemas, por lo que potenciar su desarrollo resulta esencial en la formación del futuro ingeniero.
A partir del análisis de propuestas interesantes realizadas por varios investigadores de la didáctica de la combinatoria, este artículo responde a la necesidad de sistematizar lo publicado, y estructurar su uso para potenciar el desarrollo de la habilidad resolver problemas combinatorios en los estudiantes de pregrado de la Ingeniería Informática e Ingeniería en Ciencias Informáticas.
MÉTODOS O METODOLOGÍA COMPUTACIONAL
Para la realización de la propuesta se realizó un análisis del estado del arte de la didáctica para el tratamiento del contenido combinatorio; se realizó la consulta de tesis y artículos de revistas científicas relacionados con este tema. Adicionalmente se investigó el tratamiento del contenido combinatorio llevado a cabo en libros prestigiosos que han sentado pautas en la enseñanza de la matemática discreta, y otros específicos para la enseñanza y el aprendizaje de la Combinatoria, identificando con particular interés los elementos de la didáctica particular asumidos; tal es el caso de los libros de (Johnsonbaugh, 2005), (Rosen, 2012), (Grimaldi, 2004), (Bogart, 2002), (Kolman, 1996), (Nieto, 1996), (Hernandez, 2018).
En la investigación documental resultó de particular importancia el estudio minucioso de cómo está presente la Disciplina Matemática Discreta en los Planes E de Estudio de las carreras de Ingeniería Informática e Ingeniería en Ciencias Informáticas, y de los respectivos programas analíticos de las asignaturas Matemática Discreta I y II definidos en la UCI y de la Matemática Discreta en otras universidades.
Se realizaron entrevistas individuales a diez profesores con más de un año de experiencia en la impartición de la asignatura matemática discreta II de la Universidad de las Ciencias Informáticas, y se analizaron los resultados de los informes finales del colectivo de la Matemática Discreta II al finalizar el curso 2018-2019. Se realizó un muestreo de las respuestas estudiantiles a las preguntas de combinatoria en el examen extraordinario realizado durante el curso 2018-2019 con el fin de profundizar en los tipos de errores que más persisten en los estudiantes que tienen mayores dificultades en este contenido.
A partir de sistematizar las aportaciones de las fuentes consultadas, y de identificar la necesidad de perfeccionar en los estudiantes el desarrollo de la habilidad resolver problemas combinatorios, se proponen algunas alternativas didácticas aplicadas durante el curso 2019-2020.
RESULTADOS Y DISCUSIÓN
Didáctica que se aplica en el tratamiento del contenido combinatorio
En cuanto a la disciplina Inteligencia Computacional, los planes E de estudio para la Ingeniería Informática y la Ingeniería en Ciencias Informáticas establecen que los elementos de la combinatoria en las matemáticas discretas son básicos para las probabilidades y estadística; las que a su vez sirven de apoyo para la Investigación de Operaciones, las Simulaciones y el tratamiento de la incertidumbre en la Inteligencia Artificial. Entre los objetivos de la disciplina se persigue que el estudiante aprenda a diseñar soluciones a problemas computacionales a traves del conocimiento de los fundamentos de la matemática discreta en general, y del contenido combinatorio en particular, que exige del desarrollo de habilidades relacionadas con las operaciones de la teoría de conjuntos, describir los principios básicos de la combinatoria para resolver problemas de conteo (MES. Cuba, 2019, pp. 88-91).
El tratamiento de la combinatoria transita el camino didáctico de lo simple a lo complejo. En la carrera Ingeniería en Ciencias Informáticas este contenido constituye el primer tema de la asignatura Matemática Discreta II, y a él se destinan dos conferencias y siete clases prácticas.
La primera conferencia del contenido se inicia con la presentación de los principios de la multiplicación, la suma y de las casillas; el principio de las inclusiones y exclusiones, que proviene de la teoría de conjuntos, es presentado como una generalización del principio de la suma para evitar el sobreconteo. En un segundo momento de la conferencia, el principio de la multiplicación se toma como base para la introducción de los tipos de conteo simples sin repetición de elementos, correspondientes a las r-permutaciones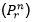 
y permutaciones 
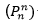de las r-permutaciones de elementos repetidos 
. La primera conferencia concluye cuando se introducen las combinaciones sin repetición tomando como base un subconjunto del conjunto de r-permutaciones dado por la relación: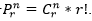 
.
En la segunda conferencia se introducen los conceptos de permutaciones y combinaciones generalizadas (con repetición de elementos) tomando como base inicial la resolución de situaciones problemáticas relacionadas con el trabajo con conjuntos de objetos indistinguibles. Los análisis realizados conducen a las fórmulas de las expresiones para el cálculo de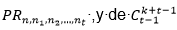 
. La Conferencia concluye con el tratamiento del teorema del binomio, su generalización, consecuencias, y vinculación con el triángulo de Pascal.
En nuestra experiencia, este contenido de la segunda conferencia es muy complejo y no son necesarios en pregrado para los objetivos de la carrera. Los contenidos de la primera conferencia son muchos, y necesitan asentarse y ejercitarse suficientemente. En las recomendaciones de la ACM-IEEE (2013) en relación al currículo para las ciencias de la computación, se especifica que como núcleo cardinal de las permutaciones y combinaciones deben ser abordadas “las definiciones básicas, las identidades de pascal y el teorema del binomio” (p. 79).
Tras la impartición de cada conferencia se destinan tres clases prácticas para el desarrollo de habilidades, la séptima clase práctica se dirige a la integración general de los contenidos. En el diseño de las clases prácticas se busca un aumento progresivo del grado de complejidad de las tareas propuestas; se trata de que a través del desarrollo de habilidades matemáticas elementales y básicas se contribuya a un mayor desarrollo de la habilidad general para resolver problemas más complejos. El estudiante en su actividad de aprendizaje debe resolver varios tipos de problemas combinatorios, algunos requieren de la aplicación de un principio o tipo simple de conteo elemental, en otros casos será necesario la combinación de más de un principio y/o tipos de conteo.
En la Figura 1, se muestra la secuencia de acciones a seguir cuando se resuelven problemas de conteo. Esta secuencia de análisis aparece reflejada en varios libros de matemática discreta (Johnsonbaugh, 2005), (Rosen, 2012), (Grimaldi, 2004), (Bogart, 2002), (Kolman, 1996), (Nieto, 1996), (Hernandez, 2018), y está respaldada por un correcto tratamiento didáctico. Con ella en mente, el estudiante debe identificar las palabras claves en los textos de los problemas que le permitan determinar si en el conteo se admiten o no elementos repetidos, y si importa o no el orden, para poder elegir la rama adecuada; y fórmulas adecuadas en el esquema de solución.
Según Dubois (1984), citado por Navarro-Pelayo, Batanero y Godino (1996; pp.3-5), es posible clasificar las configuraciones combinatorias simples en tres modelos: Selección, que enfatiza la idea de muestreo; Colocación, relacionado con el concepto de aplicación entre dos conjuntos; y Partición o división de un conjunto en subconjuntos. La aplicación de estos modelos varía cuando se añaden consideraciones relacionadas con la importancia de considerar el orden o no, la presencia o no de elementos distinguibles, y si se incluyen condiciones adicionales.
Bajo esta clasificación, en algunos casos una misma fórmula puede dar solución a problemas de diferentes modelos mientras que en otros un mismo modelo puede ser resuelto por diferentes fórmulas; De aquí que se considere que no es suficiente la preparación del estudiante que basa su aprendizaje únicamente en el esquema de la Figura 1. Adicionalmente la existencia de problemas que requieren para su solución de la combinación de principios y fórmulas eleva la cantidad de casos posibles a analizar, a esto se añade existencia de dificultades con la interpretación de textos.
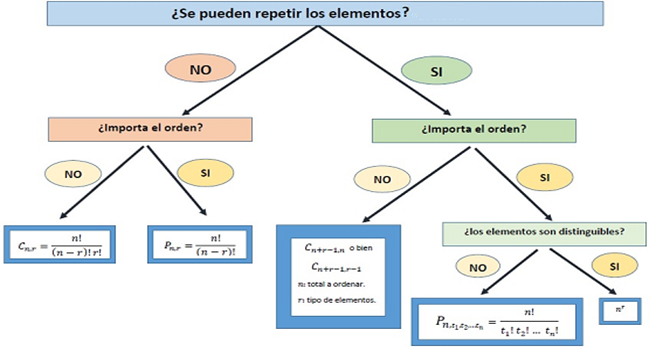
Fig. 1 Esquema para la aplicación de las fórmulas según los tipos de conteo. Fuente: Libro Matemática Discreta para Ingenieros Informáticos.
A continuación, se analiza lo que para los autores de este artículo son interesantes aportaciones que pueden contribuir a perfeccionar el proceso de resolución de problemas combinatorios
Representación de los conjuntos de resultados
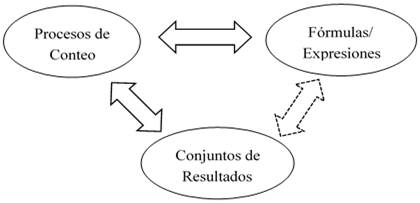
Loockwood (2013, 2014) propuso un modelo de pensamiento combinatorio para facilitar el análisis conceptual de la actividad de los estudiantes no graduados, en relación con la enumeración de objetos para su conteo. Este modelo posee tres componentes básicos: fórmulas/expresiones, procesos de conteo y conjuntos de resultados.
La componente fórmulas/expresiones se refiere “a aquellas expresiones matemáticas que conducen a un valor numérico, lo mismo pueden tener algún significado combinatorio o ser una combinación de operaciones numéricas, en ocasiones existen expresiones equivalentes. Los procesos de conteo se refieren a procesos (o series de procesos) de enumeración que un estudiante ejecuta cuanto está inmerso en la búsqueda de la solución de un problema combinatorio. Por último los conjuntos de resultados (set of outcomes) constituyen la colección de aquellos objetos que uno puede imaginar que resultan contados o generados en un proceso de conteo”(Loockwood, 2013, p. 253). En ocasiones estos objetos suelen ser muchos y dificiles de enumerar explícitamente.
Un ejemplo de conjuntos de resultados puede ser el siguiente: Si un sistema hipotético de matrículas de autos dispone de tres consonantes seguidos de cuatro dígitos y se pregunta por la cantidad de matrículas que es posible conformar, algunas placas pertenecientes al conjunto de todos los posibles resultados pueden ser: ABC1234; DEF3579; AAA1111; CBA1234; etc.
Otro ejemplo: Si una empresa tiene tres técnicos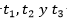 
y cuatro obreros 
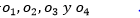y se necesita conformar un equipo de dos obreros y un ingeniero para acometer una tarea urgente, entonces el conjunto de todos los posibles resultados contendrá entre otros a los siguientes elementos: 
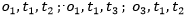etc, pero dado que no importa el orden de selección de las personas para la conformación de los equipos, sería muy correcto representarlos mediante conjuntos, es decir: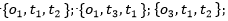 
Cada par de componentes del modelo determina un tipo de relación (ver Figura 2). Por un lado una misma fórmula/ expresión puede desencadenar diferentes procesos de conteo, ya sea por el modelo o el contexto en que se esté analizando; en sentido contrario, todos los procesos de conteo deberían conducir a una fórmula/expresión, aunque no siempre los estudiantes lo logren.
Cuando se busca la solución de problemas combinatorios, los procesos de conteo pueden conducir a ciertos conjuntos de resultados, y en sentido contrario cierto conjunto de resultados puede ser enumerado gracias a ciertos procesos de conteo; y esto es importante pues de acuerdo con Loockwood (2013) “el cardinal de un conjunto de resultados constituye la respuesta de un problema de conteo”, o sea que ” la respuesta a un problema de conteo puede ser conceptualizada como un proceso de conteo que conduce a una expresión apropiada, pero que tambien puede ser conceptualizada como la cardinalidad de un conjunto apropiado de resultados” (p. 255).
Se coincide con Loockwood (2014), quien insiste en la importancia de enseñar a los estudiantes a enfocarse en los conjuntos de resultados “… como un componente intrínseco para resolver problemas de conteo. El punto es que al adoptar esa perspectiva, la facilidad de operar con los resultados es una parte natural de cómo se enfocan y resuelven”(…)” Los estudiantes pueden evitar dificultades comunes, como aplicar incorrectamente una fórmula, contar inadvertidamente o tener problemas de orden confusos”(p. 31).
Por su parte Mneimneh y Nikolaev (2017), profesores del departamento de ciencias de la computación del Hunter College, de la Universidad de New York City, proponen facilitar la identificación y representación del tipo de situación que se describe en los textos de los problemas mediante la utilización de códigos similares a lenguajes de programación, para representar de manera estándar los tipos de conteo.
Para clarificar el proceso de conteo de las formas de realizar una actividad con varias fases Mneimneh y Nikolaev (2017) proponen:
La utilización de tuplas (delimitadas por llaves) cuando importe el orden con que se realizan las fases de una actividad.
La utilización de conjuntos (delimitados por paréntesis) si no importa el orden con que se realiza las fases de la una actividad.
El cardinal de las tuplas o de los conjuntos mencionados arriba indicará el número de fases de la actividad que se analiza.
En cada una de las fases, el conteo puede ser con repetición o sin repetición de elementos, esto debe ser declarado, así como cada uno de los elementos de los conjuntos que servirán para formar las combinaciones o k-permutaciones.
Si se realiza conteo sin repetición de elementos, el cardinal del conjunto inicial irá disminuyendo de uno en uno en cada nueva fase.
Teniendo en consideración los aspectos descritos anteriormente es posible tratar el principio de multiplicación de manera estándar.
En el mismo sentido que Lockwood (2013, 2014), los investigadores Mneimneh y Nikolaev (2017) destacan la importancia de trabajar con los conjuntos de resultados, pero ofrecen una vía para especificarlos a través de tuplas y conjuntos que luego les permite estructurar un proceso de conteo basado en las componentes de cada conjunto de resultados posibles, a modo de fases, mediante el empleo de códigos de programación, para reducir la ambigüedad para el orden y la representación.
Una tupla o n-tupla es una secuencia ordenada finita de n objetos en tanto que en la teoría informal un conjunto es una colección no ordenada de objetos. En correspondencia con lo anterior, ya en la asignatura Matemática Discreta I, los estudiantes llegaron a conocer una representación de las Máquinas de Turing basada en tuplas, y también consolidaron la definición de conjunto aportada por Cantor en 1895. Por lo que se consideró que resultaba factible la utilización de los conceptos de tuplas y conjuntos, para diferenciar aquellos conjuntos de resultados donde importa el orden de aparición de sus elementos de aquellos donde no es relevante, y para una posterior aplicación de códigos de programación.
Los elementos de los conjuntos de resultados citados en los ejemplos de las matrículas de autos, y del equipo de trabajadores de la empresa que aparecen arriba tendrán forma de tuplas: [A,B,C,1,2,3,4]; [D,E,F,3,5,7,9]; [A,A,A,1,1,1,1]; [C,B,A,1,2,3,4]; …, y forma de conjuntos: 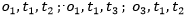…, respectívamente.
Resultados de la entrevista a diez docentes que impartieron la Combinatoria en la Facultad Introductoria de Ciencias Informáticas
Al concluir el curso 2018-2019, se realizó una entrevista individual a diez de los profesores que impartieron el tema de Combinatoria como parte de la asignatura Matemática Discreta II, en la Facultad Introductoria de Ciencias Informáticas. Entre los docentes entrevistados hay tres profesores auxiliares, uno de ellos es el jefe de la asignatura en la universidad, tres profesores asistentes y cuatro instructores; tres profesores son doctorandos en ciencias de la educación, dos de ellos realizan el doctorado en España, hay tres másteres en ciencias y otros tres cursan estudios de maestrías en ciencias matemáticas, versión pedagogía. En cuanto a experiencia impartiendo la asignatura tres profesores acumulan más de ocho cursos, otro acumula más de seis cursos, y el resto de los docentes posee dos cursos de experiencia.
Se realizó a cada profesor cuatro preguntas, todas relacionadas con el proceso de desarrollo de la habilidad resolver problemas combinatorios. En la primera pregunta se indagaba por la valoración personal de cada entrevistado acerca de la didáctica que se aplica en la enseñanza-aprendizaje para el desarrollo de la habilidad que aquí se analiza; La segunda pregunta se dirigía a conocer las mayores dificultades que enfrentan los estudiantes al resolver problemas combinatorios; la tercera interrogante se dirigía a conocer si en el proceso de enseñanza-aprendizaje de la resolución de problemas combinatorios se exigía operar con representaciones o ejemplos de conjuntos de resultados, así como con la clasificación de los problemas combinatorios, y en la última interrogante se solicitaba alguna propuesta de mejora del proceso de desarrollo de la habilidad por parte de cada consultado.
De manera general los entrevistados coinciden en que a pesar de que se siguen las indicaciones metodológicas establecidas para el tratamiento de la combinatoria y de que se cuenta con una cultura de trabajo consolidada por la experiencia acumulada durante varios cursos, es posible elevar la calidad del proceso de enseñanza-aprendizaje de manera que se revierta en una mejor capacidad estudiantil para resolver problemas más diversos, donde se evidencie mayor protagonismo, independencia e iniciativas.
En cuanto a las mayores dificultades para el desarrollo de la habilidad problemas combinatorios se señala que los estudiantes transitan por el primer año de la carrera, por lo que presentan carencias en las habilidades y hábitos que resulta necesario suplir, en algunos casos se manifiestan errores en la interpretación de textos, en la representación de lo dado y lo buscado, en la escasa o nula argumentación, en la elección del modelo de solución, y en la preferencia por el aprendizaje de fórmulas en lugar de los modelos de análisis, así como la pobre utilización de mecanismos de comprobación.
El 70% de los docentes reconoce que no utiliza de manera consciente el recurso de la representación basado en conjuntos de resultados para desarrollar la habilidad resolver problemas combinatorios en sus estudiantes, y que no exigen de su determinación sistemática en cada uno de los problemas que se proponen en clases. El 100% de los entrevistados no trabaja en clases la clasificación de los problemas combinatorios propuesta por Dubois (1984), en su lugar se trabaja la clasificación de la Figura 1.
Entre las propuestas de mejora del proceso de enseñanza-aprendizaje los profesores sugieren potenciar el trabajo intradisciplinario, utilizar las tecnologías de la información y las comunicaciones como medios de enseñanza y la utilización de formas organizativas que incentiven la participación estudiantil y su investigación.
Muestreo de las respuestas ofrecidas por los estudiantes en el examen extraordinario del curso 2018-2019
Para buscar información sobre el grado de desarrollo de la habilidad resolver problemas combinatorios en los estudiantes del primer año de la Ingeniería en Ciencias Informáticas se realizó un muestreo de las respuestas que ofrecieron los 36 estudiantes que realizaron la evaluación final extraordinaria de Matemática Discreta II, en el curso 2018-2019; todos pertenecientes a los ocho primeros grupos docentes de la Facultad Introductoria de Ciencias Informáticas (FICI).
En relación con las dos preguntas relacionadas con la combinatoria en la prueba extraordinaria, primero se solicitó la cantidad de cadenas binarias que comienzan o terminan con ciertas cantidades de unos; en la segunda pregunta se indagó por la cantidad de formas de seleccionar un equipo mixto de dos hombres y dos mujeres a partir de un conjunto de tres hombres y tres mujeres.
Una alternativa para resolver la primera interrogante consiste en aplicar el principio de las inclusiones-exclusiones sobre los resultados de las permutaciones con repetición de elementos, en tanto que la solución de la segunda pregunta requiere la aplicación del principio de la multiplicación relacionado con una actividad con dos etapas; el valor de casos en cada etapa es un número de combinaciones.
En las Figura 3 y Figura 4 se representan los porcentajes de aciertos y errores de los estudiantes en los ítems correspondientes a cada pregunta:
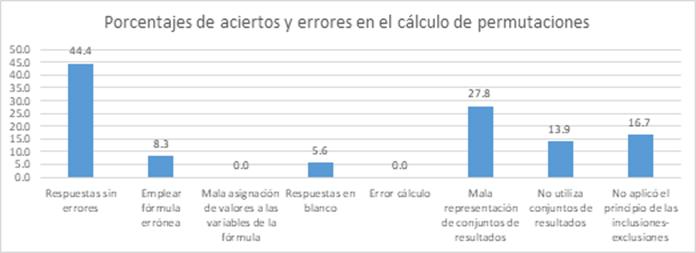
Fig. 3 Aciertos y errores de 36 estudiantes en el cálculo de permutaciones vinculadas con el principio de inclusiones-exclusiones, en el examen extraordinario del curso 2018-2019.
Comparación de los resultados en el cálculo de permutaciones, y el cálculo de combinaciones
El porcentaje de respuestas sin errores alcanzados en el ejercicio de permutaciones es superior en un 11,1% al porcentaje alcanzado en el ítem equivalente en la pregunta correspondiente a las combinaciones, aunque ambos son relativamente bajos.
En ambas preguntas resultan minoritarios los porcentajes de estudiantes que no logran identificar acertadamente el tipo de conteo requerido, en este caso se contradice la opinión de los profesores entrevistados.
En ambas preguntas se evidencia lo dicho por los profesores entrevistados en cuanto a las carencias en el trabajo con los conjuntos de resultados para facilitar el análisis de la solución de los problemas.
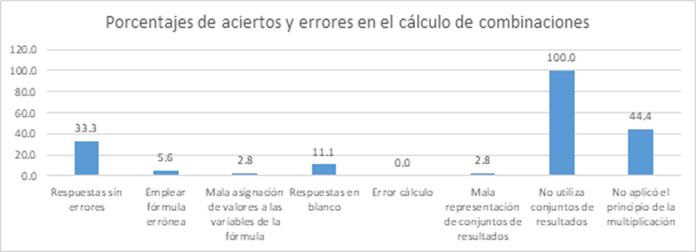
En el caso de la pregunta de combinatoria todos los estudiantes sustituyeron en la fórmula directamente sin apoyar su análisis en algún conjuntos de resultados; Un 44,4% de los evaluados no aplicó el principio de la multiplicación al limitarse a calcular los factores por separado, sin vinculación.
De manera general los porcentajes de respuestas sin errores no resultan satisfactorios por lo que se evidencian carencias en el desarrollo de la habilidad resolver problemas combinatorios.
Las conclusiones de las entrevistas a los docentes de la combinatoria, el peso de los errores cometidos en las preguntas relacionadas con las permutaciones y combinaciones, así como los insuficientes porcentajes de respuestas excelentes reflejados en las Figura 3 y Figura 4 permiten evidenciar que aún es posible perfeccionar la didáctica que se aplica en el proceso de enseñanza-aprendizaje de la resolución de problemas combinatorios; En ambas preguntas se evidencia una pobre utilización de las representaciones de los conjuntos de resultados.
A partir de los antecedentes mostrados hasta aquí, se describe una experiencia relacionada con la aplicación de un grupo de procedimientos didácticos dirigidos a perfeccionar el proceso de enseñanza-aprendizaje de este contenido. Se ofrecen además elementos de validación de la propuesta.
Didáctica para aplicar conjuntos de resultados en el desarrollo de la habilidad resolver problemas combinatorios
La base de los procedimientos didácticos que aquí se presentan opera fundamentalmente sobre el contenido, las formas de organización, los medios de enseñanza y la evaluación. El diagnóstico permanente juega un papel esencial no solo para determinar el nivel de desarrollo real de cada estudiante al inicio del proceso, sino para evaluar su desempeño individual en cada actividad, para que los profesores perfeccionen el diseño de las actividades a realizar con los estudiantes, y para contribuir a la evaluación formativa.
Los procedimientos didácticos que aquí se presentan no desdeñan el tratamiento tradicional del contenido combinatorio pero incluyen el trabajo explícito con los modelos de clasificación de los problemas combinatorios propuestos por Dubois (1984), el análisis de los conjuntos de resultados en cada problema propuesto, el empleo de metodologías que propicien la participación estudiantil, el empleo de los recursos tecnológicos que poseen los estudiantes, y la realización de una evaluación formativa. A continuación se procede a ampliar los detalles cada una de estas componentes.
En consonancia con las recomendaciones de Lookwood (2013, 2014) y de Mneimneh y Nikolaev (2017), durante el curso 2019-2020, se organizó la enseñanza-aprendizaje de la resolución de problemas combinatorios haciendo incapié en la obtención de conjuntos de resultados, pero en forma de conjuntos o tuplas, como paso inicial del proceso de modelación. Esto rompe con la práctica habitual en la que se habla de conjuntos donde importa el orden y conjuntos donde no importa el orden de aparición de sus elementos, y que contradice la definición informal de conjunto.
Para desarrollar la identificación de los tipos de problemas combinatorios, se sistematizó el trabajo con los modelos de problemas propuestos por Dubois (1984), comenzando por su presentación en la primera conferencia y la exigencia de clasificar cada ejercício trabajado en las clases prácticas; esto resulta vital pues permite fortalecer el pensamiento combinatorio del estudiante.
Con el fin de potenciar el desarrollo de la habilidad para representar conjuntos de resultados, se realizaron ejercícios en elaboración conjunta, en los que demostró su utilidad para identificar los tipos de conteo, y la presencia o no de elementos indistinguibles. Se enseñó el trabajo con diagramas de árbol y tablas como recursos de representación de tuplas y conjuntos, así como la importancia de seguir un orden cuidadoso para evitar caer en sobreconteo.
Dado que existen casos en los que aparecen conjuntos de resultados con un cardinal elevado, quedó establecido la realización de una sistematización relacionada con la obtención de patrones de los diferentes tipos de tuplas o conjuntos involucrados. Al respecto es posible orientar el estudio de los algoritmos generadores de permutaciones y combinaciones que aparecen en subsecciones de los libros de (Johnsonbaugh, 2005), (Rosen, 2014), etc.
Trabajo con las colecciones de problemas
Las colecciones de problemas trabajadas en las clases prácticas y en el estudio independiente provienen esencialmente de los libros de texto utilizados en la impartición de la matemática discreta en las carreras Ingeniería Informática e Ingeniería en Ciencias Informáticas: Matemática Discreta de Richard Jhonsonbaugh, libro excelente que contiene una cantidad inmensa de ejercicios, muchos con respuestas, y del libro en preparación: Matemática Discreta para Ingenieros Informáticos de Alién García Hernández.
Sobre los ejercicios seleccionados se realizaron algunas modificaciones:
Para contribuir a fortalecer los procesos de comprensión de los textos de los problemas, en cada ejercício fueron incluidos incisos dirigidos a indagar por el tipo de modelo de Dubois (1984) a que hace referencia el problema, y a representar los conjuntos de resultados cuyo cardinal se busca, en forma de tuplas o conjuntos. Con estos elementos se solicitó fundamentar que tipo de conteo se requiere realizar.
Se adicionó a la colección de problemas aquellos en los que se ofrece inicialmente una fórmula combinatoria simple o compuesta, y se solicita al estudiante que elabore ejemplos de conjuntos de resultados de cardinal igual al valor de la fórmula, además de la formulación de problemas que las necesiten. Esta experiencia se aplica en la Universidad Tecnológica de la Habana con buenos resultados.
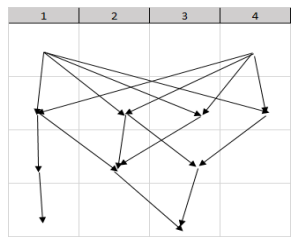
Al igual que en el item anterior se mantienen las mismas exigencias, pero en lugar de partir de fórmulas, se propone elaborar los conjuntos de resultados y problemas utilizando inicialmente diagramas de árbol o tablas. A modo de ejemplo, para representar el conjunto de resultados: {{1,1,1,1},{1,2,2,3},{1,3,2,3},{1,4,3,3}, {4,1,1,1},{4,2,2,3},{4,3,2,3},{4,4,3,3}} pueden emplearse variantes de diagramas de árbol o tabla como las que aparecen en la Figura 5 y la Tabla 1.
Tabla 1- Representación mediante una tabla del mismo conjunto de resultados presentado en la figura 5
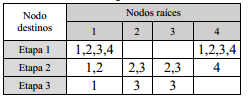
A partir del conjunto inicial {1,2,3,4}, las flechas que van de un nivel a otro del diagrama de árbol indican la existencia de relaciones entre dichos elementos; en el caso de la Tabla 1, se van listando los nodos destino en cada etapa con relación a los nodos iniciales.
Comentarios:
Producto de la irrupción de la COVID 19, al inicio del segundo semestre del curso 2019-2020, fue interrumpido el proceso de enseñanza-aprendizaje por lo que no se llegó a realizar las evaluaciones escritas parciales y finales del contenido combinatorio, solo se cuenta con los registros de la evaluación sistemática los que reflejan parcialmente que las acciones descritas en el primer item contribuyeron a disminuir el número de errores relacionados con el conteo y la comprobación, los estudiantes comprendieron de formas más objetiva las características del tipo de proceso de conteo que se necesitaba en cada problema.
En relación a las acciones descritas a partir del segundo item, los estudiantes pudieron verificar cómo una misma fórmula, diagrama de árbol o tabla era útil para modelar diferentes variantes de conteo.
Dirección de la participación estudiantil
Para estimular la participación estudiantil se solicitó la conformación por los estudiantes de equipos de dos o tres miembros. Se realizó una distribución entre los equipos de los problemas combinatorios programados para las clases prácticas, y el estudio independiente. Se solicitó a los estudiantes que enriquecieran sus respuestas con el empleo de alguna de las tecnolgías a su disposición, incluyendo las móviles y la programación.
Se prestó atención especial al cumplimiento de los principios didácticos de la unidad de lo cognitivo con lo afectivo, y del carácter educativo del proceso de enseñanza-aprendizaje. Se aceptó el cambio de los problemas originales por aquellos que despertaban el interés de los aprendices, sin afectar los objetivos didácticos.
Se fomentó el debate de las soluciones, incluyendo las variantes de respuesta a los problemas, procurando la participación de todos los estudiantes. Se promovió el debate conjunto de las soluciones elaboradas por los equipos profundizando en la causa de las formulaciones erroneas, para evitar su repetición durante el trabajo independiente.
En aras de propiciar la evaluación, coevaluación y autoevaluación, se estimuló el trabajo de los equipos en pares ponencia-oponencia, al extremo de que siempre un equipo propusiera la evaluación del otro atendiendo al desempeñado. Cada equipo tuvo la oportunidad se autoevaluar su labor. Considerando los criterios emitidos por los participantes y el nivel de cumplimiento de los objetivos trazados, el docente formuló la evaluación sistemática para los equipos y estudiantes.
Para concluir el tema se realizó un seminario final en los que cada equipo presentó un resumen de lo aprendido en el tema de estudio en vinculación con su aplicación en la esfera de la informática.
Los procedimientos didácticos aquí presentados contaron con la aprobación del colectivo de profesores de la asignatura Matemática Discreta II, con su aplicación en el curso 2019-2020.
CONCLUSIONES
El proceso de enseñanza-aprendizaje de la combinatoria que tiene lugar en la matemática discreta de las carreras relacionadas con las ciencias de la computación, se apoya en la resolución de problemas. En diversas publicaciones a nivel nacional e internacional se reflejan las dificultades que enfrentan los estudiantes de cualquier nivel, cuando resuelven problemas de combinatoria. La entrevista a profesores y el muestreo de las respuestas escritas ofrecidas por los estudiantes que realizaron el examen extraordinario de Matemática Discreta II en este contenido así lo demuestra.
El insuficiente desarrollo de la habilidad para resolver problemas queda en evidencia con los errores que comenten los estudiantes en cuanto a la nula argumentación de los pasos dados, con la incorrecta selección de la fórmula idónea al desconocer entre otras causas al modelo de la configuración combinatoria involucrada y con la comisión de errores de sobreconteo.
En el curso 2019-2020, en la carrera Ingeniería en Ciencias Informáticas, y contando con la aprobación del colectivo de profesores de Matemática Discreta, se aplicó un conjunto de procedimientos didácticos dirigidos a elevar el desarrollo de la habilidad resolver problemas de combinatoria que sistematizó el tratamiento de los modelos de selección, distribución y partición propuestos por Dubois (1984), y la representación de conjuntos de resultados en forma de tuplas o conjuntos, a través de diagramas de árbol y tablas, como vía para potenciar los procesos de interpretación de los problemas combinatorios.
Adicionalmente, los procedimientos descritos incluyeron la modificación de las colecciones de problemas, el empleo de métodos organizativos que propician el protagonismo y la participación estudiantil; así como el empleo por los estudiantes de los recursos tecnológicos de los que disponen para presentar los resultados de su trabajo. Como consecuencia de la aplicación de los procedimientos se alcanzó un mayor grado en el cumplimiento de los objetivos didácticos y educativos del tema y de la asignatura.
