INTRODUCTION
The popularity of virtual stores that include delivery services brings the necessity of efficiently planned routes to ensure the timely delivery of purchased goods and the rational use of resources. In Cuba, online stores gai ned popularity very recently with the appearance of the Covid-19 pandemic. The main online store in Cuba is the platform TuEnvio, from Cimex Corporation. In this store, the distribution routes are planned manually, lea- ding to a cumulative delay in purchase delivery; therefore the need to develop a solution to optimize the route planning process. This type of situation can be modeled as a Vehicle Routing Problem (VRP). VRPs define a class of combinatorial optimization problems that model most situations involving distribution chains (Cattaruzza et al., 2017). This problem consists in finding p routes of minimum distance to satisfy the demand of n customers, where each route is covered by a single vehicle (Cattaruzza et al., 2017). The Capacitated Vehicle Routing Problem (CVRP) is a VRP variant, where the capacity to satisfy customers’s demands of each vehicle is limited (Ralphs et al., 2003). This problem contains the bin packing problem and the Traveling Salesman Problem (TSP) at the same time (Ralphs et al., 2003). One of the approaches to solve the CVRP in the literature consists in clustering the points to their corresponding route using CPMP and determining de tour order within each route solving the corresponding TSP (Reimann et al., 2004).
The Capacitated P-Median Problem (CPMP) seeks to locate p facilities, with a limited capacity, in a way that the distance among the located facilities and assigned demand is minimum (Daskin and Maass, 2015). The P-Median Problem (PMP) is considered an NP-Hard combinatorial optimization problem; therefore, many approaches proposed to solve it involve approximated methods such as heuristic and metaheuristics. In (Whitaker, 1983) a greedy construction heuristic is proposed to solve the PMP problem. A Genetic Algorithm by (Correa et al., 2004) to solve the CPMP. In (Fleszar and Hindi, 2008) a Variable Neighborhood Search heuristic is designed to solve the CPMP problem. In (Sun, 2013) the Ant Colony metaheuristic is proposed to solve the location routing problem. An analysis of fitness landscape of Ant Colony in solving the VRP concludes that algorithm is good strategy to solve de problem due to the significant improvements of the solution obtained by each iteration (Agárdi et al., 2021). Another proposal includes the use of Iterated Local Search to solve the Hamiltonian P-Median problem (Erdog˘an et al., 2016).
Even with the use of approximated methods, finding a good solution for the CPMP is not feasible with real-size instances in terms of computational effort (Reimann et al., 2004). (Taillard, 1993) proposes two decomposi tion approaches, one for the case where clients are distributed uniformly around the depot and another when not. When clients are distributed uniformly, a partition by sectors is proposed. When the problem is very large, the sectors are also partitioned, resulting in a partition into polar regions (Taillard, 1993). For non-uniform instances, the proposed decomposition follows the logic that cities that are near each other will probably belong to the same subproblem. Another approach is proposed by (Dhaenens-Flipo, 2000) for the multi-facility pro duction and distribution problem, where a hierarchical spatial decomposition scheme is proposed consisting in grouping facilities and customers by levels and regions, taking into account geographical characteristics. Reimann et.al (Reimann et al., 2004) propose a decomposition strategy that applies a clustering algorithm to assign each client to its corresponding route. Once the clients are allocated to their cluster, the routing part of the problem is solved for each cluster. This way, a large vehicle routing problem is transformed into a group of subproblems where the Traveling Salesman Problem is solved. In (Rizkallah et al., 2019) a clustering algorithm where each client is assigned to a single route; then, each route is merged based on the distance between the clients of each route as long as capacity constraint is not violated. This approach disregards the distance between the depot and the clients, focusing in grouping the clients near to each other.
In (Putri et al., 2021) a cluster first route second approach is proposed to solve the VRP. In this proposal CPMP is used to cluster the clients in their corresponding route using Genetic Algorithm to determine the distribu- tion of the clients. In this paper a decomposition approach is proposed to solve the CVRP problem modeled as the CPMP with TSP. Furthermore, three decomposition strategies are proposed to reduce the computatio nal effort required to solve the problem. The solution method consists in decomposing large instances of the CVRP problem and model it as the CPMP. For each subproblem, the solution is obtained using Iterated Local Search algorithm. The proposed strategies are applied in a case study that involves customer locations from TuEnvio online store, to determine the decomposition strategy that achieves the routes with smaller cost and computational effort. Obtained routes are represented and analyzed, as a result, applying a PMP heuristic as a clustering algorithm to obtain the subproblems achieves good solutions in a reasonable time.
COMPUTATIONAL METHODOLOGY
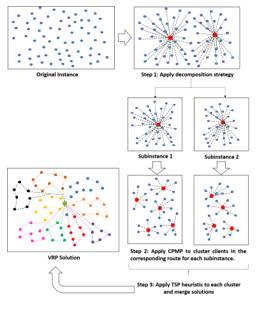
One of the approaches found in the literature to solve the Capacitated Vehicle Routing Problem (CVRP) is to adapt it to the CPMP (Morales and Rahim, 2017). The proposed scheme is depicted in Figure 1. The process starts by dividing the initial instance conformed by the location of all the clients expecting a delivery into smaller sub-instances using a heuristic procedure to solve the PMP. The obtained sub-instances are solved using a mix of the CPMP and a heuristic to solve de Traveling Salesman Problem (TSP). CPMP is used to cluster clients into their corresponding route. Each client is assumed to have a demand of a i = 1, and the required amount of clusters with capacity C j to assign all clients is defined. As for TSP, it is used to determine the delivery order of each client in its corresponding route, considering a common depot among all routes. When each subproblem has been solved, the solutions are joined to conform the solution of the initial instance.
Decomposition of instances
The CVRP is an NP-Hard problem and is very difficult to solve, especially when solving large-scale instances (Cattaruzza et al., 2017). One approach to tackle this issue is divide and conquer. In this paper, we propose three instance decomposition strategies that use the available geographic information of clients such as municipality and coordinates to derive sub-instances from the original. Each of the obtained sub-instances can be solved as VRP problem and then be integrated to conform the solution of the original instance.
Partitioning by municipalities strategy (PM)
This strategy consists in dividing the clients in a CVRP instance by municipality, obtaining a sub-instance by each different municipality. In this partitioning strategy, when the amount of clients located in a municipality exceeds a limit size defined by a parameter S, the clients of that municipality are separated from the original instance to form a new sub-instance. This approach is very similar to that used by human route planners when routes are conformed manually (Reimann et al., 2004).
RP-PMP strategy
The RP-PMP consists in dividing the clients by municipality, obtaining a sub-instance by each different municipality. Then, each sub-instance that exceeds the size limit defined by S is recursively divided solving the PMP. This process is repeated until all sub-instances obtained contain S or fewer clients. Algorithm 1 describes this procedure, receiving the instance data and the limit size of the sub-instances to be obtained.
Algorithm 1 RP-PMP decomposition strategy
 1: function RP PMEDIAN(instance,S)
1: function RP PMEDIAN(instance,S)
2:subinstances = 0/
3:if length(instance) = S then
4:subinstances.add(instance)
5:return subinstances
6:p = 2d Amount of groups
7:partition1, partition2 = PMedian(instance, p)d Apply heuristic
 8:subinstances.add(RP PMedian(partition1, S))
8:subinstances.add(RP PMedian(partition1, S))
 9:subinstances.add(RP PMedian(partition2, S))
9:subinstances.add(RP PMedian(partition2, S))
10:return subinstances
P-PMP strategy
The P-PMP strategy determines the minimum amount of divisions dividing the number of clients by S, ob- taining the required value of the parameter p that specifies the number of clusters obtained from the PMP heuristic. Algorithm 2 describes the steps to perform this strategy.
Algorithm 2 P-PMP decomposition strategy
 1: function RP PMEDIAN(instance,S)
1: function RP PMEDIAN(instance,S)
2:size = length(instance)d Size of the instance
3:subinstances = 0/
4:if size = S then
5:subinstances.add(instance)
6:return subinstances
7:p = ceil( size )d Total of groups to be obtained.
8:subinstances = PMedian(instance, p)
9:return subinstances
Local search algorithm
Most proposals to solve the CPMP consist of heuristic and metaheuristic methods (Erdog˘an et al., 2016). To solve the CVRP modeled as CPMP, we suggest the use of Iterated Local Search (ILS) (Talbi, 2009) with a greedy initial procedure and two exchange operators. Considering this, the CPMP is modeled and solved as an optimization problem using the BiCIAM framework (Fajardo, 2015), which provides an implementation of the ILS metaheuristic and the required elements to define the subordinated heuristics. After the solution of the CPMP is obtained, for each of the obtained clusters we solve the Traveling Salesman Problem (TSP) to obtain the sequence of the clients in the route.
Initial solution and perturbation procedures
To construct the initial solution used by ILS, a greedy heuristic is proposed. The proposed heuristic consists in locating the facilities that contribute less total assignment distance. These step is repeated until p facilities are located. Solutions are represented in two parts: a binary list indicating for each facility if is located or not, and a binary matrix indicating by each facility if is a demand node is assigned or not.
To explore the solution space two mutation operators are used. The first is the 2-swap (Tabrizi et al., 2011). It consists in selecting two facilities randomly, one opened, and one closed, exchanging their values.
The second operator is the greedy two-opt (Davari et al., 2013), where a roulette wheel selection of the facilities is used. The probability of selection of each facility is determined by the total distance of the demand nodes assigned to the facility respect the total distance of demand nodes assigned to all located facilities.
Solving the Traveling Salesman Problem (TSP)
The TSP is a combinatorial optimization problem that aims to find the Hamiltonian cycle with the minimum distance (Flood, 1956). Many solution methods proposed to solve the TSP involve heuristics. Farthest Inser- tion is an iterative procedure where, by each iteration, the farthest node from each of the nodes currently in the tour is inserted (Golden et al., 1980). In this paper, we use the implementation of the Farthest Insertion heu- ristic to solve the TSP provided by the Open Source Routing Machine (OSRM) under the service Trip (Luxen and Vetter, 2011).
RESULTS AND DISCUSSION
The proposed case study is designed to determine the best instance decomposition strategy of the ones propo- sed, and analyze the obtained solutions. The decomposition strategies are applied over 16 instances of different sizes. The instances are obtain by an aleatory sampling of 18000 client locations provided by CIMEX Corpo- ration. For each route, a maximum capacity of C j = 40 clients is considered. For each decomposition strategy, an S = 600 limit is defined. The ILS metaheuristic is executed 15 times with 10000 iterations. The metrics to measure the performance of the strategies are travel time and execution time.
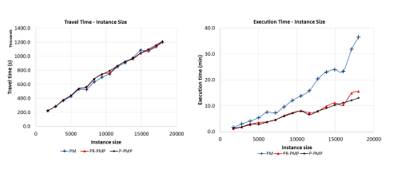
Figure 2 shows the obtained average travel times and execution times respectively, using the proposed decom- position strategies for each instance. As can be noted, the three proposed strategies exhibit a similar travel time across all instances, although PM strategy most times achieves better travel times. As expected, travel times increase with the number of clients and therefore routes. In the case of execution times, PM strategy shows a more rapid growth than PR-PMP and P-PMP strategies, therefore achieving the worst execution times.
Solution representation
Figure 3 shows the 44 routes obtained by each decomposition strategy, for an instance of 1700 customers. In the representation, the circles represent customers’s locations, while the lines represent the route. As it can be seen, the clients closest to each other are part of the same route, except more isolated clients that are grouped in larger routes.
To provided a more detailed representation of routes obtained, municipalities Marianao and Plaza, with 104 and 195 clients respectively, are enlarged in Figure 3. The clients allocated to a rout outside these municipalities are represented by a black triangle. As can be noted, the clients of each route are closely grouped to each other, reducing the distance between each client. Another aspect to note is that in routes obtained with PR- PMP and P-PMP strategies there is less overlapping of clients in different routes, as opposed to PM strategy. In Plaza municipality, using the PM strategy, most of the clients are grouped within five routes, except some clients located to the north and south of the municipality, which are covered by other routes. The five routes obtained with the PM strategy add a total of 129km. With PR-PMP, most clients are grouped in six routes, except some clients to the east side. The total distance of the six routes obtained with PR-PMP is 129,6km. Finally, with P-PMP decomposition, most clients are grouped in four main routes and two routes from other municipalities marked in yellow and brown. Some clients from the northeast border are satisfied with routes that contain mostly clients from other municipalities. The total distance among the six routes obtained with P-PMP is 147,2km.
In the case of the municipality of Marianao, using the PM Strategy groups all clients in 3 routes, with a total length of 122km. As for PR-PMP and P-PMP strategies, most clients are grouped in 3 main routes, leaving 4 clients to be attended by other routes that mostly cover clients from other municipalities. Routes obtained with the PR-PMP strategy accomplish a total length of 122km. As for the P-PMP strategy, the total distance of the three routes is 123,2km. Note that one of the three routes obtained with PR-PMP and P-PMP not only cover the clients within the municipality of Marianao, also cover clients from adjacent municipalities, as opposed to the PM strategy.
As can be noted some clients are not allocated to routes within their corresponding municipality in the three examples shown. This is due to the instance size limit S defined as 600. Since the amount of clients of these municipalities does not exceed the 600 clients limit, none is considered as separated instance, therefore the clients can be allocated to routes of different municipalities.
CONCLUSIONS
This paper supports the following conclusions:
The Capacitated Vehicle Routing Problem can be modeled using Capacitated P-Median Problem com- bined with the Traveling Salesman Problem due to the common characteristics among them.
The division of the original instance in smaller subproblems using PM strategy obtains short routes, but a higher computational effort is required compared to the other two strategies.
Instance decomposition using the PR-PMP strategy obtains solutions with a travel time 0,02 % higher than PM strategy, with 45,6 % less computational effort than PM strategy. Therefore, it offers the best solution quality-computational effort compromise.
The proposed solution scheme provides routes conformed by customers close to each other. This allows the recirculation of vehicles in case a client was not available, with a smaller travel distance.
Routes obtained with PR-PMP and P-PMP present less overlapping than routes from the PM strategy, reducing the intersection between routes.
The proposed solution can be an effective tool for enterprises involved in logistic distribution chains, especially when trying to reduce operational costs. As a recommendation for future works we suggest the study of the effects of other metaheuristic algorithms to obtain a solution in terms of computational effort and solution quality. We also suggest the comparison of solution methods to classic formulations of the VRP and our proposal.