ARTÍCULO ORIGINAL

 

Biblioteca de algoritmos para el particionado 2D y su problema inverso

 

Library of algorithms for obtaining 2D partitioned and his inverse problem

 

 

Yaisel Siverio Santa Teresa^1*, Romanuel Ramón Antunez², Lidisy Hernández Montero ¹

¹GEYSED. Universidad de las Ciencias Informáticas, Carretera a San Antonio de los Baños, km2 1/2, Torrens, Boyeros, La Habana, Cuba. CP.: 19370, {ysst, lhernandez}@uci.cu
²FICI. Universidad de las Ciencias Informáticas, Carretera a San Antonio de los Baños, km2 1/2, Torrens, Boyeros, La Habana, Cuba. CP.: 19370, [e-mail]

*Autor para la correspondencia: [e-mail]

 

 

---

RESUMEN

La presente investigación describe la realización de una biblioteca de algoritmos para obtener particionados 2D, utilizados para modelar componentes en el entorno de un Sistema de Información Geográfica 2D, SIG-2D. Se utiliza como base para el desarrollo de la misma, los algoritmos de Voronoi directo, inverso e inverso generalizado. La biblioteca propuesta permite obtener particionados de figuras en 2D y su problema inverso, destacándose como algoritmo fundamental el inverso generalizado de Voronoi 2D. Para guiar el proceso de desarrollo se hace el uso de la metodología Agile Unified Process y se hizo uso de una mezcla entre las arquitecturas N-Capas y orientada a objetos. Se define para su implementación el uso de tecnologías de escritorio, con el lenguaje de programación C++. Todas las tecnologías empleadas en su desarrollo son libres.

Palabras clave:biblioteca, modelado bidimensional, particionado bidimensional, Voronoi

---

ABSTRACT

This research describes the realization of a library of algorithms for 2D partitioned, used to model components in the environment of a 2D GIS, GIS-2D. It is used as a basis for the development of the same, Voronoi algorithms direct, inverse and generalized inverse. The proposed library allows for partitioned figures in 2D and inverse problem, highlighting the fundamental algorithm Voronoi generalized inverse. To guide the development process using Agile Unified Process methodology is made, using the fusion of N-Layers architectures and object-oriented. It is defined for implementation using desktop technologies with the programming language C ++. All technologies used in its development are free.

Key words: dimensional modeling, library, two-dimensional partitioning, Voronoi.

---

 

 

INTRODUCCIÓN

La Geometría Computacional es una rama de las ciencias computacionales que se encarga del diseño y análisis sistemático de algoritmos y estructuras de datos, necesarios para la solución eficiente de problemas que implican como entrada y salida objetos geométricos. Sus orígenes se remontar siglos atrás, el primer algoritmo de Geometría Computacional nace luego de que una serie de pasos correctos no ambiguos y con un final resuelven un problema geométrico; el precursor: Euclides. Es sólo a principios de 1970 que Michael Shamos comienza un estudio sistematizado de problemas, obsesionado con la idea de crear una nueva disciplina de las ciencias de computación, a la cual llamó Geometría Computacional (GC) (Shamos, 1999).

Dentro de la GC el Diagrama de Voronoi (DV) es una de las estructuras más estudiadas, debido al amplio dominio de aplicación que tiene. Esta estructura se define como sigue: Sea P = {p1,p2,p3,....pn} un conjunto de n puntos en el plano denominados sitios, se llama DV al conjunto de regiones o teselas Vor(pi), una para cada pi que pertenece P, de forma tal que cualquier punto q que pertenece a Vor(pi) cumple que . Una definición análoga a la anterior puede ser extendida a 3D, donde el problema gana en complejidad y finalmente se obtiene en vez de un particionado del plano, el particionado de un poliedro.

Ejemplos de aplicación inmediata de esta estructura se aprecian en los Sistemas de Información Geográfica (SIG), al ser una de las funcionalidades básicas que deben proveer estos sistemas; principalmente para análisis de proximidad, meteorológicos o de influencias en entornos 2D, véase (de Breg, y otros, 2008). Esta última se ve reflejada, en la cobertura hospitalaria, cercanía de estaciones de bomberos o de trenes, centros comerciales, control del tráfico aéreo o telefonía móvil. No son estas sus únicas aplicaciones ya que el campo de utilidad de esta estructura es más basto de lo que puede imaginarse, por ejemplo, en palabras de José Ramón Gómez:

“Las aplicaciones en el área de astronomía, mediante la partición basada en el análisis de métodos del modelo de puntos para la investigación de la estructura espacial de varias poblaciones estelares, o en el área médica podemos hallar la reconstrucción tridimensional computarizada y análisis cuantitativo de neuronas y de haces dendríticos en la corteza cerebral.” (Gómez)

Actualmente en los centros GEYSED y CEMC, pertenecientes a la Universidad de las Ciencias Informáticas (UCI), están definidos proyectos asociados a SIG y procesamiento de imágenes. En GEYSED es de especial atención la Plataforma de desarrollo SIG-WEB denominada GeneSIG, la cual no cuenta actualmente con soporte para la obtención de DV, lo que dificulta el desarrollo de aplicativos con capacidad para análisis de problemas de proximidad. Mientras en CEMC se trabaja en un proyecto internacional con el CIMNE para el desarrollo de un SIG-3D con la restricción de no usar ningún componente desarrollado por terceros, y la necesidad de realizar análisis de proximidad e influencias a la vez que se optimiza tiempo de procesamiento y capacidad de almacenamiento.

A partir de la problemática descrita anteriormente se deriva el siguiente problema de investigación: ¿Cómo facilitar la obtención de particionados 2D y la resolución de su problema inverso, sin usar componentes de terceros, en aplicaciones SIG de forma que permitan realizar análisis de proximidad y favorezcan la compresión de datos?

El objetivo general es desarrollar una biblioteca de algoritmos para la obtención de particionados 2D y su problema inverso.

 

MATERIALES Y MÉTODOS

Metodología utilizada

Las metodologías de desarrollo de software constituyen el conjunto de procedimientos, técnicas, herramientas y soporte documental que ayuda a los desarrolladores a realizar un nuevo software. Representan un marco de trabajo que tiene entre sus principales funciones: guiar, planificar, estructurar, controlar, manipular y dirigir el proceso de desarrollo de sistemas de información (Jacobson, y otros, 2000).

Se define AUP como la metodología más adecuada para el desarrollo del módulo, esta se basa en la gestión de riesgos, proponiendo que aquellos componentes con alto riesgo tengan más prioridad que los demás y sean desarrollados en etapas tempranas del proyecto. Desarrolla prototipos ejecutables durante la fase de elaboración del producto, demostrando la validez de la arquitectura para los requisitos claves del producto y determinando los riesgos técnicos. En AUP se establecen cuatro fases: Concepción, Elaboración, Construcción y Transición, que transcurren de manera consecutiva y que acaban con hitos claros alcanzados.

1. Concepción: Identificación del alcance y dimensión del proyecto, propuesta de la arquitectura y del presupuesto del cliente.

2. Elaboración: Confirmación de la idoneidad de la arquitectura.

3. Construcción: Desarrollo incremental del sistema, siguiendo las prioridades funcionales de los implicados.

4. Transición: Validación y despliegue del sistema.

Se eligió esta metodología porque permite guiar proyectos de una complejidad y volumen no muy altos y que necesitan una rápida implementación, los cuales son los aspectos fundamentales a tener en cuenta para el desarrollo del producto a obtener.

Herramienta de Modelado

Con el objetivo de realizar una correcta planificación, diseño, implementación y documentación del proceso de desarrollo de la biblioteca se hace uso de herramientas CASE. Estas herramientas son utilizadas con frecuencia para lograr una mejor productividad, eficiencia y eficacia de los productos informáticos, así como la reducción del tiempo de construcción de los mismos y posibles errores que estos puedan poseer.

Visual Paradigm en su versión 8.0, se considera una de las herramientas CASE más adecuada para realizar el proceso de modelado de un software, esta propiedad es básicamente la que constituyó un hecho determinante en su selección para ser utilizada en el modelado de la propuesta de solución. Posee una interfaz fácil de utilizar y es una herramienta UML que soporta todo el ciclo de desarrollo del software: análisis y diseño orientados a objetos, construcción, pruebas y despliegue.

Lenguaje de programación

C++ es un lenguaje de programación derivado del C que soporta la programación orientada a objetos y la estructurada. Fue creado a mediados de los años 80 por Bjarne Stroustrup con el fin de agregar funcionalidades y características de las que carecía su antecesor, mantiene ventajas en cuanto a riqueza de operadores, expresiones, flexibilidad, concisión y eficiencia. Además, ha eliminado algunas de las dificultades y limitaciones del C original. Actualmente es uno de los lenguajes más potentes a nivel mundial, en gran medida esto se debe a que es un lenguaje compilado. Desde el punto de vista de los lenguajes orientados a objetos, C++ es un lenguaje híbrido y existen varios IDE que lo soportan como: Eclipse y Qt Creator (Lenguajes de programación, 2009) (Louden, 2004) (Programación en castellano, 2011).

Debido a las necesidades existentes de seleccionar un lenguaje de programación rápido y eficiente con el cual el equipo de desarrollo se encuentre familiarizado y que brinde las condiciones óptimas para la construcción exitosa del software, se ha llegado a la conclusión de que el lenguaje a utilizar es C++.

Entorno de desarrollo integrado (IDE)

Un entorno integrado de desarrollo (en inglés Integrated Development Environment) es un programa informático compuesto por un conjunto de herramientas de programación, que proveen facilidades a los programadores para escribir códigos y agilizar el proceso de desarrollo de software. Pueden ser aplicaciones por sí solas o ser parte de aplicaciones existentes, además permiten ser utilizadas tanto con un único lenguaje de programación como con varios de estos. Las herramientas que normalmente componen un entorno de desarrollo integrado son las siguientes: editor de texto, compilador, intérprete, herramientas para la automatización, depurador, diseñador para la construcción de interfaces gráficas de usuario y, opcionalmente, un sistema de control de versiones (Rodríguez, 2011; IDE, 2012; Alvarez, 2010).

 

RESULTADOS Y DISCUSIÓN

La biblioteca contará con una representación de las principales soluciones propuestas por diversos autores referentes a los problemas de particionado del plano 2D. Principalmente centrándose en los problemas inversos e inversos generalizados. A continuación, se hace una breve descripción de dos de los algoritmos que formaran parte de la biblioteca.

Problema inverso generalizado de Voronoi (Almaguer, y otros, 2007).

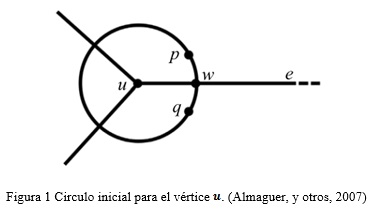
La idea seguida por el algoritmo consiste en poner pares de puntos (centinelas) a través de cada arista del GP (un centinela por cada sitio) con el objetivo de “garantizar” la arista. El número de centinelas necesarios para proteger una arista depende de su longitud y de su posición respecto a sus aristas vecinas, pues son situados al largo de las aristas para proteger, siempre a cierta distancia fijada por sus vecinas. Cada par de centinelas son situados sobre la circunferencia de algún círculo, cuyo centro yace en la arista y este no toca a ninguna otra arista. A continuación, se detalla el proceso formalmente.

Supongan que se tiene un grafo planar G=(V,E) al que se le desea aplicar el algoritmo, este trabaja con dos fases fundamentales: primeramente se construyen círculos iniciales centrados en cada vértice de G, luego se procede a cubrir cada arista e E por círculos interiores no solapados cuyo centros tienen origen en e.

Sea u un vértice de G, y la longitud de la menor arista G incidente en u. Denótese como a ambos lados de cada arista incidentes en u, uno por cada lado de e (a una distancia adecuada ).

Sea w el intercepción entre y e, ahora p y q protegen al segmento aparecerá en el DV que será construido, mientras no sean incluidos próximamente, nuevos puntos dentro de . Ver Figura 1

Sea e = una arista de G, w1,w2 los puntos de intersección de y con e respectivamente. Los segmentos están ahora garantizados, mientras que el segmento (quizás vacío) permanece desprotegido. Con el propósito de proteger es necesario cubrirlo con círculos (interiores) centrados en él, mientras que estos no intercepten alguna arista distinta de e y no incluyan algún centinela perteneciente a otro círculo.

Entonces podemos escoger pares de centinelas en cada círculo a una distancia de e. Ver Figura 2

Como consecuenca del Lema 1 el segmento e queda protegido en toda su longitud, siempre que luego no se incluya algún punto dentro de cualquiera de los círculos centrados en e se acerquen a una distancia ' de otra arista f pueden caer, dentro de algún círculo perteneciente a e. Teniendo en cuenta lo anterior se puede garantizar que los centinelas de e no interfieran con las aristas, ya que estos no estaran incluidos en ningún otro círculo perteneciente a otra arista.

El algoritmo puede describirse de la siguiente manera:

Este algoritmo, en efecto, muestra una estrategia general que brinda una variada gama de posibilidades a la hora de ejecutar los pasos 3 y 5. Con el objetivo de probar que el algoritmo trabaja debemos demostrar que:

1. El algoritmo termina.

2. Una vez ejecutado toda arista de la teselación queda protegida.

Para mostrar que el algoritmo termina se deben dejar claros algunos aspectos. Sea P0  el radio, el menor círculo inicial; es claro (por definición de círculo inicial) que P0 > 0. Sea el menor de los ángulos formados por las aristas incidentes de G, digamos e y f. Tomando a se puede estar seguros que dos pares de centinelas, pertenecientes, uno a e y otro a f, no se mezclarán, lo que quiere decir, que los pertenecientes a e no estarán a una distancia menor que ' de f, lo que garantiza que un centinela de una arista no interfiera en otra. Esto es válido para todos los círculos iniciales.

Una vez que los círculos iniciales han sido construidos y sus correspondientes conjuntos de centinelas encontrados, permanecen sin proteger, un segmento intermedio de cada arista. Dicho segmento debe ser cubierto por un número finito de círculos interiores.

Tómese una arista, dígase e, con un segmento intermedio sin cubrir de longitud , tomando círculos de radio para cubrilo podemos estar seguros que ninguno de ellos se interceptará con algún otro perteneciente a otra arista.

Exactamente círculos serán suficintes para cubrir completamente el segmento desprotegido, donde quizás el último de estos tendra radio p1 < . Para este último los centinelas pueden ser situados a una distancia ' < de e. Ver Figura 3.

Usar círculos de radio es, entre las variantes a considerar la que produce mayor cantidad de círculos y como consecuencia, de centinelas (generadores del DV). Suponiendo que todos los círculos interiores tendrían un radio igual a la ^_ vecindad escogida, si es la longitud de e (mayor arista de G=(V,E)) y P0  el radio de menor círculo inicial construido en G, S el conjunto de puntos (sitios) generados y F el conjunto de regiones de G, entonces e puede cubrirse con círculos no sola pados de radio, generandose 2() + 4 puntos si generalizamos este análisis entonces pero se puede encontrar un cota aún inferior si hacemos el análisis arista por arista: donde e es la longitud de e, p0, p1 el radio de los círculos iniciales centrados en el vértice que define e. Se puede asegurar ahora que

Tesalación inversa de Laguerre (Duan, y otros, 2014)

Una teselación Laguerre, también llamado un diagrama de potencia o un diagrama de Laguerre, es una versión ponderada de la conocida teselación de Voronoi.  A continuación, se explican algunas de las notaciones matemáticas por las que este se rige y se describirá un algoritmo que permite obtener dicha teselación. Para más detalles sobre las teselaciones Laguerre ver (Okabe, y otros, 1999).

Sea p y p un valor fijo, llamado peso del punto p. Llamamos a la par (p,w) un punto ponderado. Para toda x , definimos el poder de x con respecto a (p,w) como

Supongamos que son un conjunto de puntos finitos ponderados (generadores) en la Red. La teselación  Laguerre P divide a en células, utilizando el poder de dichos punto. La celda asociada con el i-ésimo punto generador, Ci, se define por

Tenga en cuenta que, si todos los pesos son iguales, la teselación Laguerre se reduce a la teselación de Voronoi estándar.

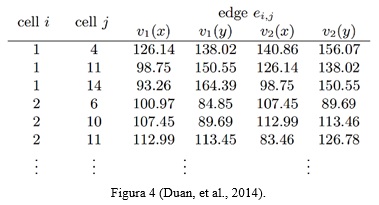
Observación 1. Las teselaciones Laguerre son un conjunto de puntos finitos localmente, pero un conjunto de puntos infinitos de generadores puede definirse de la misma manera. Ver Figura 4

Cuando todos los pesos son positivos, cada punto generador ponderado (p,w) P se puede interpretar y visualizar como una esfera (denotada por S(p,r)) con un radio con centro en el punto p. El poder un punto x con respecto a la esfera S(p,r) está dado por pow(x, S(p,r)) =

Geométricamente, esto significa que para un punto x fuera de la esfera S(p,r), el valor de pow(x, S(p,r)) es igual a la longitud al cuadrado de la línea tangente de x a S(p,r). El límite entre dos células adyacentes generadas por las esferas S1 = S(p1,r1) y S1 = S(p2,r2), se compone de todos los puntos z tal que pow(z, S1)= pow(z, S2). Estos puntos forman un hiperplano H(S1,S2) donde

Este límite es perpendicular a la línea que une p1 y p2 y se denomina eje radical de S1 y S2. En esta investigación, solo se van a considerar las teselaciones Laguerre en . En este caso, los generadores pueden interpretarse como círculos.

Una teselación Laguerre se puede representar matemáticamente como un gráfico geométrico o una colección de vértices V = {v1, v2, ....., vm} (también V(P)) y los bordes {(vi,vj)}, donde los vértices son asignados a posiciones en el espacio. Tenga en cuenta que algunas células no sólo están limitadas por segmentos, sino también por las rectas que se extienden hasta el infinito en una dirección determinada, porque se consideraron conjuntos finitos de generadores. Tales bordes se representan a menudo usando un vértice "ficticio". Es decir, un vértice del borde está dispuesto a ser un punto arbitrario en la recta que se extiende hasta el infinito, véase (Schoenberg, y otros, 2003). Los vértices interiores de la teselación tienen el mismo poder con respecto a por lo menos tres círculos separados. Por el contrario, los vértices 'ficticios' sólo tienen igual poder con respecto a dos círculos. El uso de la representación anterior, los vértices y los bordes de las teselaciones Laguerre se pueden almacenar en el formato dado en la Tabla 1.

Las células se marcan de 1 a n. Las dos primeras columnas de la Figura 4 corresponden a las etiquetas de células adyacentes. Por ejemplo, la célula es adyacente a las células 4, 11 y 14. Las coordenadas de los vértices del borde que separa dos células se dan en las columnas 3-6. Tenga en cuenta que una representación más compacta se puede lograr mediante el almacenamiento de las coordenadas de cada vértice, junto con los índices de los vértices adyacentes.

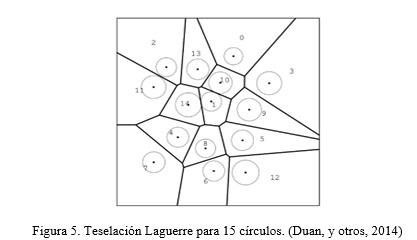
Se denomina teselación normal de Laguerre cuando las células adyacentes están cara a cara, es decir, (en 2D) que comparten bordes y vértices; Además, cada borde limita con exactamente dos células, y cada vértice es compartido por exactamente tres células. Un ejemplo de un teselado normal Laguerre 2D, generada por 15 círculos, se da en la Figura 5. Los límites entre las células son los bordes de la gráfica geométrica. Las competencias de los puntos en cada límite son iguales con respecto a los dos círculos vecinos. Observe que el grado de cada uno (interior) es el vértice 3.

Los poderes de los vértices son, por tanto, igual con respecto a los tres círculos vecinos. Ver Figura 5

A partir de ahora, consideramos solamente las teselaciones normales Laguerre 2D, por ejemplo, cuando los puntos del generador están al azar y uniformemente elegidos dentro de un área de muestreo limitada, la teselación es normal con probabilidad 1.

Propiedades

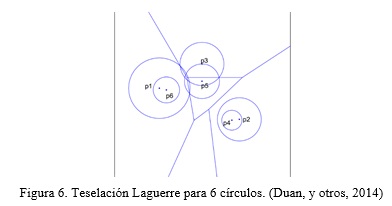
Una propiedad de la teselación Laguerre no contiene necesariamente su generador y un generador no necesariamente genera una célula.

Esta propiedad es bien conocida (véase, por ejemplo, (Aurenhammer, 1987)). Figura 6 (a partir de (Aurenhammer, 1987), (Lautensack, 2007)), muestra que el punto de una célula Laguerre generador puede estar fuera de su celda; en particular, p4 se encuentra fuera de la célula 4. La misma figura muestra un círculo generador, S(p6,r6), para los que la célula Laguerre correspondiente está vacía. Una consecuencia de la propiedad 1 es que el generador dado para una teselación no es único. Es decir, se puede añadir círculos que no generan células adicionales, y el nuevo sistema dará como resultado la misma teselación Laguerre que el original. Sin embargo, incluso cuando cada círculo genera una célula, los generadores de una teselación Laguerre no son necesariamente únicos.

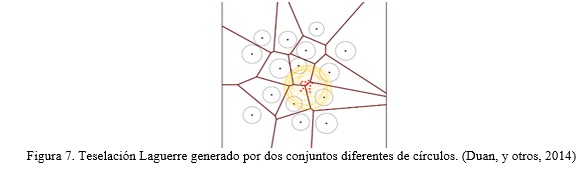
1 - Dos conjuntos completamente diferentes de los círculos pueden generar la misma teselación Laguerre.

Un ejemplo extremo se muestra en Figura 7, donde tanto los círculos grises y círculos de color amarillo dan la misma teselación. La propiedad 2 se ha mencionado en la literatura (véase (Lautensack, 2007), (Aurenhammer, 1987)). Sin embargo, no es sorprendente que haya recibido poca atención. En particular, no se ha hecho hincapié en que dos conjuntos completamente diferentes (tanto en localización y radios) de círculos pueden generar la misma teselación.

Generación de una teselación Laguerre mediente puntos ponderados

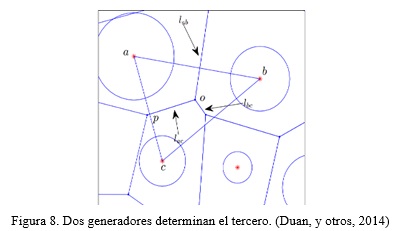
Se comenzará describiendo cómo, por una teselación dada (normal), se pueden determinar un conjunto de puntos ponderados generadores especificando sólo las coordenadas y el peso de un punto generador ponderado además de una coordenada y del punto generador ponderado de una célula vecina. Ver Figura 8

Teorema 1. Los puntos generadores ponderados de una teselación normal Laguerre 2D dados pueden ser completamente determinados desde el punto generador ponderado de una celda interior, y una coordenada del punto generador ponderado de una celda adyacente.

Prueba. Por razones de simplicidad se asume que los pesos de los puntos de generador son positivos, aunque la prueba no utiliza esta suposición. La ventaja es que los puntos de generador ponderados se pueden interpretar como círculos; Véase la Figura 4. Sea S1(p1,r1) el círculo generador de alguna celda interior, C1 y S2(p2,r2) el círculo generador de una celda adyacente a C2. Siendo las coordenadas de P1 y P2, (x1,y1) y (x2,y2) respectivamente.

Suponiendo que x1,y1, r1,x2 se tiene como datos.

Siendo e_1,2 el borde de la teselación de separación C1 y C2. Para las teselaciones Laguerre, el segmento de línea que une p1 y p2 es perpendicular a e_1,2. Tomando m_1,2 como la pendiente de e_1,2. De ello se desprende que y2 es determinada por (Tenga en cuenta que es posible que m_1,2 ,esto no es relevante en aplicaciones prácticas. El problema puede ser resuelto, por ejemplo, mediante la rotación de la teselación. Por lo tanto, se supone la pendiente sea diferente de cero.) A partir de esto se puede determinar r2 mediante para cualquier punto q en la línea que contiene el segmento e_1,2. En particular, podemos tomar q = p_1,2 , la intersección de la línea a través p1 y p2 y la línea que contiene el borde e_1,2.

Debido a que la teselación se supone que es normal y C1 es una célula interior, hay una célula adyacente tanto a C1 y C2 como a C3, la generación del círculo C3, S3=(p3,r3), se determina de la siguiente manera. El punto P3 = (x3, y3) es la intersección de (1) la línea que pasa a través de p1 y es perpendicular a e_1,2 (el borde entre C1 y C3) y (2) la línea que pasa a través de p2 y es perpendicular a e_1,2 (el borde entre C2 y C3). De ello se desprende que las coordenadas x3 y y3 de p3 satisfacen donde m_1,2 y m_2,3 son las pendientes de e_1,2 y e_2,3 ,respectivamente. Por lo tanto, El radio, r3, se determina entonces como en (2); es decir, donde q es cualquier punto de la línea que contiene el borde e_1,3 .También es posible determinar r3 considerando el par C2, C3 en lugar de C1, C3, dando donde q es cualquier punto de la línea que contiene el borde e_2,3 . Para probar que (5) y (6) dan el mismo valor para es suficiente para demostrar que donde u es el vértice en la intersección de las líneas que contienen los bordes e_1,2 y e_2,3 . Pero esto se desprende directamente de la definición de la teselación Laguerre, y el hecho de que u se encuentra también en la línea a través del borde e_1,2 . Procediendo de esta manera, es posible determinar de forma iterativa el círculo generador de cada celda.

Observación 2. El teorema 3.1 se da en 2D, pero la idea de la prueba es aplicable para las dimensiones más altas. El uso de vectores normales de hiperplanos separados por células, por ejemplo, los bordes en 2D o caras planas en 3D, está claro que los generadores deben estar en líneas con la misma orientación. Ver también (Aurenhammer, 1987), donde se da una construcción no única para la ortogonal, dual de un teselado Laguerre (en el caso de Voronoi esto corresponde a la triangulación de Delaunay).

Observación 3. La demostración del Teorema 3.1 muestra que, si añadimos la misma constante a todos los radios al cuadrado, la teselación no cambia. A saber, si para cada q en un borde que separa las células adyacentes Ci y Cj, se cumple de igual forma si son sustituidos por Como consecuencia de ello, siempre es posible encontrar un conjunto de generadores todos con pesos positivos. Si algunos pesos son negativos, simplemente encontrar el mínimo de éstos y restar este valor a todos los pesos.

El teorema 3.1 y la observación 3 sugieren el siguiente algoritmo para determinar los círculos generadores de un teselado Laguerre, dado x1, y1, r1 y x2. Observamos que en el algoritmo puede empezar con un par de células (internas) (C1,C2). Estas pueden ser reemplazadas por cualquier par de células internas durante el reetiquetado.

Algoritmo 1 proporciona un método para recuperar los círculos de generación de una teselación dado un pequeño número de entradas, es decir, x1, y1, r1 y x2.Sin embargo, dependiendo de cómo se seleccionen estas entradas, se podrán obtener resultados muy diferentes. Aunque el algoritmo garantiza pesos positivos, en algunos casos los círculos de generación pueden estar lejos fuera de las células que generan. Un ejemplo se da en la Figura 7. En otros casos, los radios de círculo generador pueden ser mucho más grande que las células o incluso la ventana de observación; véase la Figura 9.

Como se ha indicado anteriormente, muchas aplicaciones basadas en teselaciones Laguerre atribuyen significado a los círculos de generación. Por esta razón, es importante que se tenga un método que elija una solución que satisfaga criterios como los enumerados anteriormente. Algunos de estos criterios son dependientes del modelo. Otros, sin embargo, son bastante universales. En particular, es casi siempre deseable tener puntos de generación que se encuentren dentro de las células que generan y es casi siempre deseable tener radios de valor real.

En (Duan, et al., 2014) se hace alusión a otro algoritmo utilizando una técnica estocástica de interpolación global denominada entropía cruzada (CE).

 

CONCLUSIONES

Al realizar un estudio detallado de los conceptos fundamentales, algoritmos y las herramientas similares a esta investigación, se dio cumplimiento a los objetivos planteados con la conclusión de la biblioteca para realizar el particionado 2D y problema inverso (BP2DIN). De manera que esta cumpliera los requisitos funcionales establecidos para lograr las metas trazadas con la realización de un paquete de clases que muestra su funcionalidad con resultados satisfactorios.

Al ser el diseño del paquete de clases adaptable a los posibles cambios, posibilita que se puedan agregar nuevas funcionalidades en versiones posteriores sin hacer grandes modificaciones. Esto aumentaría la utilidad de la biblioteca con vistas a confeccionar un producto cada vez más completo y eficaz.

En esta primera versión de la BP2DIN el aporte principal ha sido el desarrollo de una biblioteca de clases y un manual de trabajo y uso de los algoritmos para el particionado del plano que brinda al desarrollador de aplicaciones informáticas, tales como SIG, software de diseño y compresión de imágenes, etc., una serie de facilidades para implementar el módulo de particionado del plano, específicamente, el cálculo de sitios, la generación de DV y la resolución de su PIV y PIVG respondiendo a las necesidades del usuario en menor tiempo. Además de mejorar, fácil y rápidamente, las aplicaciones que necesiten cálculos de proximidad, así como su robustez. Los programadores pueden concentrarse en los aspectos especializados de su aplicación eliminando la dependencia de especialistas en el tema de particionados del plano.

 

REFERENCIAS BIBLIOGRÁFICAS

ALMAGUER, DANIEL TRINCHET Y ROSÉS, HEBERT PÉREZ. 2007. Algoritmo para solucionar el problema inverso generalizado de Voronoi. La Habana : Revista cubana de Ciencias Informáticas, 2007.

DE BREG, MARK, Y OTROS. 2008. Computational Geometrics: Algorithms and Applications. Tercera. s.l. : Springer, 2008, 7.

ALVAREZ, ELAINE MORALES. 2010. Módulo de Gestión de Errores de la Plataforma de Televisión Informativa PRIMICIA. Ciudad de la Habana : s.n., 2010.

AURENHAMMER, F. 1987. Power diagrams: properties, algorithms and applications. SIAM Journal onComputing, 16, 78–96.

DUAN, QIBIN, y otros. 2014. Inverting Laguerre Tessellation. Australia : The Computer Journal, 2014.

GÓMEZ, JOSÉ RAMÓN. Diagramas de Voronoi. Matemática Aplicada, Universidad de Sevilla. Sevilla : s.n. págs. 8-12.

OKABE, A, Y OTROS. 1999. Spatial Tessellations: Concepts and Applications of Voronoi Diagrams. Segunda. s.l. : John Wiley and Sons, 1999. págs. 6-12.

LENGUAJES DE PROGRAMACIÓN. 2009. Lenguajes de programación. [En línea] 2009. [Citado el: 10 de enero de 2015.]   HYPERLINK "http://www.lenguajes-de-programacion.com/lenguajes-de-programacion.shtml"  http://www.lenguajes-de-programacion.com/lenguajes-de-programacion.shtml .

LOUDEN, KENNETH C. 2004. Lenguajes de programación: principios y prácticas. Mexico  : s.n., 2004.

LAUTENSACK, C. 2007. Random Laguerre Tessellations. PhD thesis Karlsruhe Institue of Technology.

PROGRAMACIÓN EN CASTELLANO. 2011. Programación en castellano. Qt Creator, un completo entorno de desarrollo . [En línea] 2011. [Citado el: 10 de diciembre de 2015.]HYPERLINK http://www.programacion.com/noticia/qt_creator-_un_completo_entorno_de_desarrollo_1723

NOKIA. 2012. QT. Sitio oficial de QT. [En línea] 2012. [Citado el: 24 de enero de 2012.] http://qt.nokia.com/products.

GARRIDO, SALVADOR ALEMANY. 2009. Introduccion a QT. Programacion grafica en C++ con Qt4. 2009.

SCHOENBERG, F. P., FERGUSON, T., AND LI, C. 2003 Inverting Dirichlet tessellations. The ComputerJournal, 46, 76–83.

RODRÍGUEZ, RAÚL LUGO. 2011. Análisis, diseño e implementación del subsistema de Transmisión de la plataforma de televisión informativa PRIMICIA versión 2.0. La Habana, Cuba : s.n., 2011.

IDE. 2012. Entornos de desarrollo integrado. Concepto de IDE. [En línea] 2012. [Citado el: 25 de enero de 2012.]   HYPERLINK "http://petra.euitio.uniovi.es/~i1667065/HD/documentos/Entornos%20de%20Desarrollo%20Integrado.pdf"  http://petra.euitio.uniovi.es/~i1667065/HD/documentos/Entornos%20de%20Desarrollo%20Integrado.pdf

SHAMOS, M. I. 1999. The early years of Computational Geometry, a personal memoir. s.l. : Contemporary Mathematics, 1999. págs. 313-332.

 

 

Recibido: 15/08/2016
Aceptado: 02/11/2016