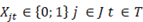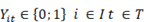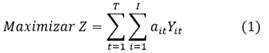Serviços customizados
Espanhol (pdf)
Artigo em XML
Referências do artigo
Enviar este artigo por email
Citado por SciELO 
Similares em
SciELO 
Permalink
INTRODUCCIÓN
Gran cantidad de problemas de optimización pueden ser encontrados en muchas situaciones reales y modeladas como un Problema de Cobertura (CLP). De este problema se derivan dos variantes: Problema de Localización de Máxima Cobertura (MCLP por sus siglas en inglés) y el Problema de Localización de Conjuntos (SLCP por sus siglas en inglés). En el SCLP se tiene como objetivo cubrir todos los nodos de demanda con un número mínimo de instalaciones, mientras que en el MCLP el objetivo es maximizar la cobertura sobre los nodos de demanda con un número conocido de instalaciones (Zarandi et al., 2013). El MCLP fue presentado por primera vez por Church y ReVelle en 1974 (Church and ReVelle, 1974) y desde entonces se han hecho numerosas aplicaciones y teorías al modelo clásico del MCLP (Murray, 2013). En cada problema la decisión se basa en buscar la mejor combinación de las p instalaciones que tenga un máximo de cobertura sobre la demanda de los nodos. Durante muchos años el MCLP ha sido objeto de varias investigaciones aplicándose en muchas situaciones reales tales como: localización de las estaciones de la policía y patrullaje policial (Curtin et al., 2010; Guarín et al., 2015; Chawathe, 2007), distribución de redes de celulares (Tutschku, 1998; Erdemir et al., 2008), localización de antenas (Farahani et al., 2012; Wei and ReVelle, 2015), localización de estaciones de taxis (Rezazadeh et al., 2018) entre otras.
Algunas clases de problemas de optimización son relativamente fáciles de resolver, sin embargo, muchos otros tipos de problemas de optimización son muy difíciles de resolver. La idea intuitiva de problema “difícil de resolver” queda reflejada en el término científico “NP-Duro”. Un problema de optimización difícil es aquel para el que no se puede garantizar la mejor solución posible en un tiempo polinomial. La existencia de una gran cantidad y variedad de problemas difíciles, que aparecen en la práctica y que necesitan ser resueltos de forma eficiente, impulsó el desarrollo de procedimientos eficientes para encontrar buenas soluciones, aunque no fueran óptimas (Martí, 2006).
El modelo MCLP es un problema NP-Duro (Tutschku, 1998) y varios autores (Church and ReVelle, 1974; Murray and Church, 1996; Adenso-Díaz and Rodríguez, 1995), han utilizado técnicas de solución aproximadas, tanto heurísticas como metaheurísticas para resolver el problema, lográndose muy buenos resultados y alcanzado así un alto prestigio. De este problema se conoce la variante de dinamismo o multiperíodo (DMCLP por sus siglas en inglés), la cual es un modelo más real del problema, ya que considera varios períodos de tiempo y ayuda a los decisores a elaborar planes en un rango de tiempo prolongado teniendo en cuenta las variaciones de la demanda (Fajardo, 2015).
Los métodos heurísticos de construcción son procedimientos iterativos que, en cada paso, añaden un elemento hasta completar una solución. Usualmente son métodos deterministas y están basados en seleccionar en cada iteración, el elemento con mejor evaluación (Martí, 2006). Los algoritmos heurísticos de construcción son normalmente muy rápidos y devuelven soluciones razonablemente buenas. La base de los algoritmos constructivos es formada por los llamados algoritmos voraces (Greedy) (Stutzle and Ruiz, 2018). Algunos algoritmos metaheurísticos inician con una fase constructiva en la generación de solución inicial para resolver los problemas de optimización. Los métodos usados en la fase constructiva en una metaheurísticas juegan un rol importante en la eficiencia del algoritmo. Los enfoques aleatorios y voraces son dos estrategias principales usadas en la generación de soluciones iniciales (Talbi, 2009).
Los métodos heurísticos constructivos también han sido empleados para la resolver el problema MCLP (Church and ReVelle, 1974; Kuehn and Hamburger, 1963; Feldman et al., 1966). Algunos autores (Downs and Camm, 1996; Xia et al., 2019) han utilizado heurísticas constructivas basadas en algoritmos voraces en la generación de solución inicial de los algoritmos metaheurísticos para resolver el MCLP. Sin embargo, al revisar la literatura se puede apreciar que es escasa la variedad de heurísticas constructivas aplicadas al modelo dinámico del MCLP, fundamentalmente en la fase constructiva de los algoritmos metaheurísticos. La variante DMCLP es un modelo más real del MCLP y el uso de heurísticas en combinación con las metaheurísticas brindaría una mejor calidad en la solución. En este trabajo se propone una modificación de cuatro heurísticas de construcción dinámicas, basadas algoritmos voraces estáticos, para revolver el DMCLP, con el objetivo que exploren el espacio de soluciones como estrategia de inicialización en las técnicas metaheurísticas.
El artículo presente está estructurado de la siguiente manera: Sección 1 Materiales y métodos o Metodología computacional se realiza revisión de la literatura relacionada con la investigación, definición del problema DMCLP y descripción de las heurísticas voraces propuestas. En la Sección 2 Resultados y discusión realizan el marco de experimentación para conocer qué solución es la más adecuada para el modelo propuesto. Finalmente, en la Sección 3 Conclusiones se presentan las conclusiones finales que guían la línea a seguir para la continuidad de la investigación.
MATERIALES Y MÉTODOS O METODOLOGÍA COMPUTACIONAL
Revisión de la Literatura
Desde su surgimiento, diversos son los métodos aplicados al MCLP como son las heurísticas de construcción basadas en algoritmos Voraces (Greedy). Los algoritmos voraces son algoritmos simples de diseñar, sin embargo, no es fácil de entender su capacidad y limitaciones. Un algoritmo voraz está diseñado para dar soluciones de buena calidad en poco tiempo y resuelve un problema de optimización global haciendo una sucesión de decisiones localmente óptima (Dzatora and Dzatorb, 2015). En esta sección se realiza una revisión del estado del arte de las heurísticas Voraces aplicadas a las variantes del modelo MCLP.
En el año 1963 Kuehn y Hamburger (Kuehn and Hamburger, 1963) propusieron uno de las heurísticas más conocidas para los problemas de Localización de Instalaciones (FLP por sus siglas en inglés) conocido como el Procedimiento Adición (ADD). Según plantea esta heurística, la ubicación que produce la mejora máxima del valor objetivo será seleccionada para colocar una instalación, y este procedimiento se repite hasta que todas instalaciones hayan sido ubicadas. Luego en 1966, Feldman y colaboradores (Feldman et al., 1966) propusieron una heurística similar, a la anterior, pero en sentido inverso llamada Eliminar (GD) para el FLP. Este método inicia con instalaciones localizadas en todos los sitios de instalaciones potenciales y elimina aquellas instalaciones que tienen el menor impacto en la función objetivo. En 1974, Church y ReVelle (Church and ReVelle, 1974) extendieron el procedimiento ADD para el MCLP y lo renombraron como Adición Voraz (GA). La idea básica de esta heurística es seleccionar un sitio potencial que maximice la mejora de la demanda cubierta total en cada ronda recalculando la demanda no cubierta en cada iteración. El procedimiento termina cuando se abren las p instalaciones. Otra heurística desarrollada por Church y ReVelle (Church and ReVelle, 1974) fue la heurística de Adición Voraz con Sustitución (GAS), desarrollado para obtener una solución más satisfactoria que la solución obtenida por el procedimiento GA.
En 1996, Haghani (Haghani, 1996) utilizó también la técnica GA para resolver el MCLP con capacidad (CMCLP por sus siglas en inglés). Se basa en que cuando una facilidad es añadida la demanda asignada es recalculada, similar a la propuesta realizada por Church y ReVelle (Church and ReVelle, 1974). En 1998 además de los métodos básicos GA y GAS, Hochbaum y Pathria (Hochbaum and Pathria, 1998) diseñaron una heurística con enfoque voraz para el MCLP, que selecciona el subconjunto que brinda la mejora máxima en cuanto a término de la cobertura del conjunto. Los resultados obtenidos fueron muy positivos, lográndose una buena solución. Ese mismo año, Saldanha y Captivo (Saldanha and Captivo, 1998) utilizaron heurística GD y búsqueda local, implementado todo ello en CPLEX, para resolver un problema de localización discreta dinámica con establecimientos y eliminación de costos. Luego en el 2008, Indriasari (Indriasari, 2008) propuso una variante del MCLP, llamado Problema de Área de Servicio Máximo (MSAP por sus siglas en inglés). El objetivo del modelo es maximizar el área de servicio total, dado un número fijo de instalaciones. Dos algoritmos voraces: GA y Adición Voraz con Evaluación Tiempo de Viaje (GAT), fueron propuestos para solucionar el problema de MSAP. Los algoritmos GA y el GAT produjeron una mejor cobertura que la cobertura existente, teniendo el mismo número de estaciones de bomberos.
En el 2009, Ahmad Rodzi Mahmud y Vini Indriasari (Rodzi and Indriasari, 2009) propusieron dos algoritmos heurísticos voraces, la heurística GA y GAS para resolver el MSAP, desarrollado para maximizar el servicio total de un número fijo de facilidades, resultando ambas muy eficientes en dar solución al problema, sin tener mucha diferencia en sus resultados. En el 2015, Pratap (Pratap, 2015) propuso una heurística voraz llamada Gran Paso (GBS) para el modelo MCLP. Se realizó una comparación del algoritmo propuesto con un algoritmo voraz clásico y un algoritmo aleatorio, mostrando resultados satisfactorios en comparación con los dos últimos. Por último, en 2016, Bulut y Szymanski (Bulut and Szymanski, 2016) diseñaron una variante del MCLP con restricciones adicionales específicas. Adoptan la variante de despliegue de AP WIFI con la demanda máxima satisfecha usando un número definidos de AP, donde pueden ser considerados algunas restricciones adicionales. Para resolver este modelo hacen uso del GAS, el cual mostró muy buenos resultados.
Definición y Representación del DMCLP
Los problemas de localización de instalaciones se aplican a una gama muy amplia de situaciones reales y por ello cada día ganan un gran interés en el ámbito de investigación de operaciones (Murray, 2016). Entre los problemas de localización se encuentra el problema de máxima cobertura (MCLP), conocido como uno de los modelos clásicos de la literatura (Church and ReVelle, 1974).
El objetivo de su modelo era maximizar la cobertura de la población con recursos. Desde su surgimiento hasta la actualidad se han desarrollado distintas variantes del modelo clásico de MCLP. En el año 1980 Schilling (Schilling, 1980) propone una variante dinámica del modelo multiobjetivo de localización (MODL por sus siglas en inglés). Gunawardane (Gunawardane, 1982) sugiere una extensión dinámica del modelo MCLP (DMCLP) a diferencia del clásico maximiza la cobertura en múltiples períodos. Zarandi en (Zarandi et al., 2013) propone una variante dinámica donde se conoce el número de instalaciones a ubicar sin preferencia sobre el número de instalaciones que se ubicarán en cada período. A continuación, se describen los parámetros y variables del modelo del problema DMCLP (Zarandi et al., 2013).
Parámetros:
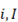: posición y conjunto de nodos demanda.
j, J: posición y conjunto nodo de instalación.
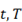: Índice y cantidad de periodos de tiempo.
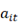: demanda del nodo 
en el periodo 
.
: Distancia de un nodo de demanda en el período t.
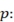cantidad de instalaciones a ubicar teniendo en cuenta todos los periodos de tiempo T.
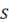: Radio de cobertura de las instalaciones.
: { j|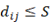
}es el conjunto de instalaciones cuya distancia al nodo 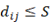es menor que 
.
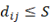Variables:
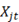: variable binaria que para el valor 1 significa que la instalación j en el periodo t está abierto.
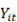: variable binaria que para el valor 1 significa que el nodo de demanda 
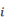en el periodo t está siendo cubierto, 0 en caso contrario.
La función objetivo del problema es:
Maximizar la suma de la demanda de los nodos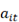 
para aquellos 
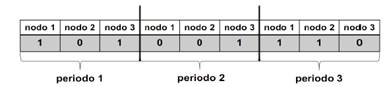= 1 en todos los periodos de tiempo.
Sujeto a:
Donde la restricción (2) establece que la cantidad de instalaciones abiertas en T periodo de tiempo debe ser igual al valor p y la (3) establece que un nodo de demanda en un periodo t solo pude ser cubierto si se encuentra dentro del radio de cobertura S de al menos una instalación abierta en el mismo periodo t.
Aunque muchos enfoques diferentes pueden ser empleados para representar una solución de DMCLP, en este empleamos una representación de cadena binaria en el cual cada bit representa el estado del nodo (Zarandi et al., 2013), donde el valor 1 significa que esa instalación se encuentra abierta o disponible y 0 en caso contrario (Fajardo, 2015). La Figura 1 se muestra un esquema de representación de una solución para T períodos (Zarandi et al., 2013).
Algoritmos Heurísticos y Metaheurísticos
La necesidad de encontrar soluciones buenas de problemas difíciles en un tiempo razonable es otra de las razones para usar métodos heurísticos. El método heurístico es más flexible que el método exacto, permitiendo, por ejemplo, la incorporación de condiciones que son difíciles plantear. Las heurísticas se usan como parte de un procedimiento global que garantiza la búsqueda de la solución óptima de un problema. Hay muchos métodos heurísticos que son muy diferente en la naturaleza. Por consiguiente, es difícil de proporcionar una clasificación exacta. Además, muchos de ellos se han diseñado para resolver un problema específico sin la posibilidad de generalización o aplicación a otros problemas similares (Martí and Reinel, 2011). En (Martí and Reinel, 2011) plantean los métodos constructivos como uno de las clasificaciones de métodos de resolución mediante heurísticos. Consisten en construir literalmente paso a paso una solución del problema. Usualmente son métodos deterministas y suelen estar basados en la mejor elección en cada iteración.
El término metaheurística fue introducido por Fred Glover en 1986 (Glover, 1986) quien lo define de la siguiente manera:
«Una metaheurística es referida a la estrategia maestra que guía y modifica otras heurísticas para producir soluciones más allá de aquellas que son normalmente generadas en la búsqueda de un óptimo local. Las heurísticas guiadas por una estrategia meta pueden ser un procedimiento de alto nivel o pueden contener una descripción de movimientos permitidos para trasformar una solución en otra, conjuntamente con una regla asociada de evaluación».
Heurísticas Voraces para resolver el DMCLP
A continuación, se describirán cuatro heurísticas voraces para resolver el DMCLP.
Adición Dinámica Voraz (GAD)
El procedimiento GA aplicado al problema de localización de máxima Cobertura (MCLP) fue presentado por Church y ReVelle (Church and ReVelle, 1974). La idea básica de la heurística es seleccionar un sitio potencial que maximice la mejor demanda cubierta total en cada iteración. Este proceso es continuo hasta que se hayan seleccionado p instalaciones o toda la población esté cubierta (Church and ReVelle, 1974).
El funcionamiento del algoritmo Adición Dinámica Voraz (GAD) es muy parecido a la variante estática, la única diferencia es que se deben abrir las instalaciones a lo largo del tiempo. El algoritmo comienza seleccionando el sitio potencial que cubre la mayor cantidad demanda y escoge el período donde tiene su mayor cubrimiento en la demanda, ubicando así la primera instalación en ese período. Los criterios de la segunda instalación es determinar el sitio que cubre la mayor cantidad de demanda, no cubierta por la primera instalación. Para ello reevalúa nuevamente la cobertura total de cada sitio potencial por período, no teniendo en cuenta las demandas cubiertas del período seleccionado de la primera instalación. El procedimiento se repite hasta que el conjunto de elementos seleccionados constituya una solución, es decir se haya seleccionado p instalaciones.
Adición con Sustitución Voraz Dinámico (GASD)
El procedimiento GAS aplicado al MCLP fue presentado también por Church y ReVelle (Church and ReVelle, 1974). El algoritmo GAS para la variante dinámica (GASD) comienza ubicando sus instalaciones en cada iteración del mismo modo que lo realiza el algoritmo GAD. La diferencia se establece en que las instalaciones fijas obtenidas como las mejores no son añadidas aún al conjunto de solución final, antes se verifica si las propuestas de instalaciones fijas a ubicar pueden ser reemplazadas por otros sitios potenciales. El GASD realiza la posible sustitución mediante un análisis en cuanto a la ganancia en la cobertura general, y el sitio potencial que cumpla la mayor ganancia es la que sustituye a la instalación fija, ubicando la nueva instalación en el mejor periodo de dicho sitio potencial, en caso contrario, de existir pérdida en la cobertura general, la instalación fija analizada se mantiene. El algoritmo es continuo hasta que se haya analizado todas las instalaciones fijas, ubicando finalmente las instalaciones resultantes al conjunto de solución. En otras palabras, el algoritmo GASD determina nuevas ubicaciones en cada iteración como el algoritmo GAD y además trata de mejorar la solución en cada iteración mediante la sustitución, o intercambio de instalaciones.
Eliminación Voraz Dinámica (GDD)
La heurística GD fue presentado en 1966 por Feldman, Lehrer y Ray (Feldman et al., 1966). El algoritmo GD comienza con todos los sitios potenciales instalados, y en cada iteración elimina la instalación que tenga el menor decremento en la función objetivo. La variante Eliminación Voraz Dinámica (GDD) funciona del mismo modo. A diferencia del algoritmo clásico, el GDD verifica en cada iteración que los nodos de demanda que cubría la instalación eliminada, estén cubiertos en otras instalaciones, y aquella instalación que contenga la mayor demanda cubierta es la que se le asigna los nodos de demanda de la instalación eliminada. Posteriormente se recalcula la cobertura total de cada instalación. Este procedimiento es continuo hasta que solo queden abiertas las p instalaciones. Finalmente, el algoritmo GDD ubica las p instalaciones en los mejores t periodos de tiempo de cada instalación seleccionadas como las mejores.
Gran Paso Voraz Dinámico (GBSD)
El algoritmo GBS para el problema de localización de máxima cobertura fue presentado por Pratap (Pratap, 2015). El algoritmo Gran Paso Voraz para la variante dinámica (GBSD) se le incorpora un nuevo elemento denominado período de tiempo. En cada iteración el algoritmo evalúa todas las posibles K combinaciones de sitios de instalaciones potenciales formadas del conjunto y busca la combinación de instalaciones que en su unión contengan el mayor número de elementos cubiertos. Se añade después al conjunto las K instalaciones en el período donde su sumatoria es la de mayor incremento en la demanda cubierta. Este proceso es continuo hasta que se haya seleccionado p instalaciones. Este algoritmo tiene como restricción que las K combinaciones de sitios potenciales que se formen tienen que ser menor o igual que las p a ubicar, así mimo la p tienen que ser mayor que 1. Cuando las K combinaciones de sitios potenciales a formar sea menor que p, ejemplo K=2 y p=3, el algoritmo realiza combinaciones de dos en la primera corrida y en la próxima corrida K tomaría valor 1, ubicando así las 3 instalaciones.
RESULTADOS Y DISCUSIÓN
En esta sección se realiza una descripción experimental para evaluar la efectividad de los algoritmos voraces propuestos aplicados al DMCLP. Con el fin de evaluar el rendimiento de los algoritmos y sus resultados se aplican pruebas estadísticas no paramétricas. Para verificar si existen diferencias significativas en los algoritmos propuestos y para obtener el algoritmo de mejor rendimiento se aplica test Friedman (Friedman, 1937). Para evaluar si el mejor algoritmo en cada caso tiene un rendimiento significativamente diferente a los demás, se aplicaron los test post-hoc: Holm (Holm, 1979), Finner (Finner, 1993) y Li (Li, 2008), con un nivel de significación de α = 0.05. La herramienta Keel (García et al., 2009) fue la seleccionada para realizar los test estadísticos.
Inicialmente se describen las características de las instancias utilizadas en los experimentos y la configuración de los algoritmos. Con el objetivo de evaluar el comportamiento de los algoritmos voraces, se ejecuta de manera independiente los algoritmos propuestos y se realiza un análisis comparativo para seleccionar la variante que mejor resultado obtuvo. Por último, las mejores heurísticas se comparan con el algoritmo metaheurístico Escalador de Colinas con solución inicial por ruleta y con solución inicial Voraz.
Descripción de la experimentación
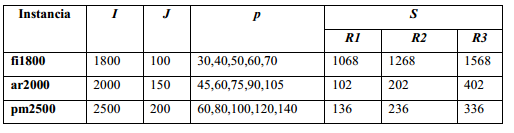
Se seleccionaron tres instancias de la librería TSP-Lib (Reinelt, 1991): ar6723, pm4951 y fi10639. De ellas se seleccionó aleatoriamente un conjunto de puntos para los nodos de demanda con una 𝐼 de 1800 a 2500 puntos y para las instalaciones una 𝐽 de 100 a 200. Se realizaron diferentes combinaciones de radios de coberturas y cantidad de instalaciones a ubicar. En la Figura 2 se muestra una visualización de las instancias originales de TSP-Lib, de las cuales se crearon las instancias para la experimentación.
La p representa el 30, 40, 50, 60 y 70 % de J. En la Tabla 1 se muestra la descripción de los diferentes elementos de las instancias. Para la experimentación con el algoritmo Escalador de Colinas se realizaron 30 ejecuciones y 10000 iteraciones, para todas las instancias.
Análisis y comparación de las Heurísticas Voraces de manera independiente
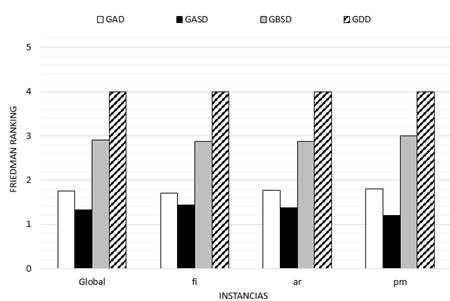
A continuación, se explican los resultados de comparar las heurísticas propuestas entre ellas. En los resultados del test de Friedman, ilustrado en la Figura 3 el p-valor en todas las instancias y de forma global fue igual a 0, por lo que es menor que 0.05 y se rechaza la hipótesis nula. Entre las heurísticas sí existen diferencias significativas. Según el ranking que ofrece el test de Friedman, el algoritmo GASD fue el mejor algoritmo en las instancias fi1800, ar2000 y pm2500 siendo así el mejor algoritmo de manera global.
En la Tabla 2. Resultado de la Prueba no paramétrica de Friedman post-hoc Holm, Finner y Li. para las distintas Instancias se muestran los resultados de los post-hoc Holm, Finner y Li. El signo “>” significa que el algoritmo A se comportó mejor que el B, y “-” quiere decir que no hay diferencias significativas, o sea que no hay evidencias suficientes para rechazar la hipótesis nula. Se compara el algoritmo que mejor ranking obtuvo de forma global en la prueba de Friedman, el GASD, con los restantes algoritmos.
Tabla 2 Resultado de la Prueba no paramétrica de Friedman post-hoc Holm, Finner y Li. para las distintas Instancias
El resultado obtenido en la Tabla 2 muestra que el GASD se comportó mejor que el GDD y GBSD de forma global ya que el p-valor es menor que 0.05, por tanto, se rechaza la hipótesis nula y sí existen diferencias significativas entre los comportamientos de los algoritmos. Hay que destacar que el algoritmo GASD en esta prueba tuvo un comportamiento similar al algoritmo GAD en todas las instancias y de forma global donde no hubo diferencias significativas.
Análisis y comparación del Escalador de Colinas con Solución Inicial por Ruleta y Heurísticas Voraces
En esta sección se realiza un análisis con el Escalador de Colinas (Bagherinejad et al., 2017) utilizando en su solución inicial algoritmos voraces y ruleta propuesto en (Zarandi et al., 2013). Los algoritmos voraces seleccionados fueron lo que obtuvieron mejores resultados en el análisis anterior, en este caso el GASD y el GAD. Se pretende con este experimento demostrar la calidad de la solución de las heurísticas voraces sobre el problema propuesto.
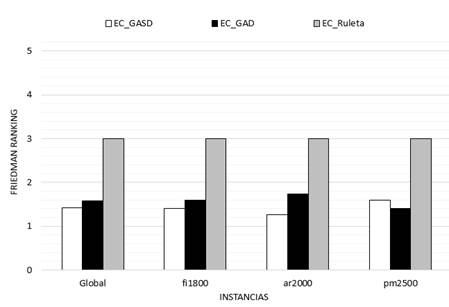
En la Figura 4 se muestra una gráfica de los resultados obtenidos al aplicar el Test de Friedman. El p-valor en todas las instancias y de forma global fue igual a 0, por lo que es menor que 0.05 y se rechaza la hipótesis nula. Ello implica que sí existen diferencias significativas entre los comportamientos de los algoritmos. Según el ranking que ofrece el test de Friedman, la combinación EC_GASD fue el mejor algoritmo en las instancias fi1800, ar2000 y EC_GAD fue mejor en la instancia pm2500. De forma global el algoritmo EC_GASD fue el de mejor rendimiento.
En la Tabla 3 se muestran los resultados de los post-hoc Holm, Finner y Li para todas las instancias, donde se compara el algoritmo que mejor ranking obtuvo de forma global en la prueba de Friedman, el EC_GASD, con los restantes algoritmos. Se puede concluir que no hay diferencias significativas entre el algoritmo EC_GASD y EC_GAD ya que tuvieron un comportamiento similar por lo que no existen evidencia para rechazar la hipótesis nula. El algoritmo EC_GASD se comportó mejor que el EC_Ruleta.
CONCLUSIONES
Los algoritmos voraces han sido aplicados a una gama amplia de problemas de optimización entre los que se encuentra el MCLP, dado a la rapidez y calidad en la solución que brindan. La variante dinámica del MCLP es un modelo más real del clásico, ya que al considerar varios períodos de tiempo se pueden tomar decisiones en un rango de tiempo prolongado teniendo en cuenta fluctuaciones de la demanda. Los algoritmos voraces propuestos en esta investigación para la variante dinámica obtuvieron resultados satisfactorios. De los algoritmos voraces propuestos, el que mejor comportamiento obtuvo de manera global fue el algoritmo GASD, aunque no hubo diferencias significativas con el algoritmo GAD. En el último análisis comparativo, los algoritmos GAD y GASD como solución inicial del Escalador de Colinas brindaron soluciones de mejor calidad en comparación con la solución inicial utilizando ruleta dentro del algoritmo metaheurístico Escalador de Colinas. Las heurísticas voraces utilizadas como estrategia de inicialización en los algoritmos metaheurísticos obtienen buenos resultados para resolver el modelo DMCLP.
