ARTÍCULO ORIGINAL

Generador de valores interesantes para casos de pruebas unitarias

Generator of interesting values for unit test cases

Dania Mailen Rojas-Robert^I  , Zeyla Pérez-Morales^I  , Martha Dunia Delgado-Dapena^II 

^IComplejo de Investigaciones Tecnológicas Integradas, CITI. La Habana, Cuba. Correo eletrónico: [e-mail], [e-mail]

^IIUniversidad Tecnológica de La Habana, José Antonio Echeverría. La Habana, Cuba. Correo eletrónico: [e-mail]

RESUMEN

Es de gran importancia, dentro de las pruebas de software, el diseño y la creación de pruebas eficaces asociadas a una adecuada generación de valores de prueba, pues las pruebas empíricas, no garantizan la detección de todos los errores, y la prueba exhaustiva es muy costosa en tiempo y esfuerzo. Por tanto, la estrategia es tratar de hacer las pruebas lo más abarcadoras posibles al tener en cuenta un subconjunto de los posibles casos y valores de prueba con mayor probabilidad de detectar errores. En este contexto, surge la necesidad de utilizar técnicas de diseño de casos de pruebas para la generación automática de los datos de prueba que garanticen obtener altos niveles de cobertura de errores. Este trabajo presenta una propuesta de generación de valores interesantes para pruebas unitarias, de forma automática, utilizando las técnicas de diseño de Bucles y Condiciones.

Palabras-clave: pruebas de software; valores de prueba; técnicas de diseño de casos de prueba; prueba de Bucles; prueba de Condiciones

ABSTRACT

An activity of vital importance in software testing is the design and creation of effective test cases associated with adequate generation of test values, because empirical tests can´t guarantee detection of all errors and the exhaustive testing is very costly in time and effort. Therefore, the strategy is try to make the tests the most inclusive possible to consider a subset of possible cases and test values most likely to detect errors. In this context, the need arises for using test case design techniques for the automatic generation of test cases, which ensure high levels of error coverage. This paper presents a component that generates automatically, values for unit testing, using design techniques Loops and Conditions.

Key words: software testing; test values; technical design test cases; test loops; test conditions

I. INTRODUCCIÓN

Debido al avance de la tecnología, las empresas modernas han sustentado sus principales procesos en sistemas de software, razón por la cual la aceptación por parte del cliente se torna en un requisito elemental y su calidad cobra una especial importancia ^[1]. Una actividad del proceso de desarrollo de software, que asiste de manera efectiva la calidad, son las pruebas. Estas consisten en probar una aplicación mediante técnicas experimentales, en las distintas fases del ciclo de vida, lo que facilita el proceso de cotejo y evidencia la calidad del software ^[2,3]. Por estos motivos, el éxito de las pruebas depende del descubrimiento de un error no detectado hasta entonces, para lo que requieren de un diseño de casos de prueba con la mayor probabilidad de evidenciar fallos ^[2].

Existen dos enfoques de pruebas: las pruebas de caja negra y las pruebas de caja blanca^[2]. Las pruebas de caja negra, también denominadas pruebas de comportamiento, se centran en los requisitos funcionales del software. Las pruebas de caja blanca, denominadas también pruebas de caja de cristal, utilizan la estructura de control del diseño procedimental para obtener los casos de prueba.

Las pruebas unitarias, en las que se basa este trabajo, están específicamente encaminadas al enfoque de caja blanca ya que centran el proceso de verificación en la menor unidad del diseño: el módulo, la clase, el método, entre otros. Estas utilizan la descripción del diseño detallado como guía, para probar los caminos de control importantes, con el fin de descubrir errores en la unidad ^[2,4].

Existen herramientas comerciales que automatizan la ejecución de las pruebas unitarias de software; sin embargo, el diseño de casos de prueba continúa en manos de los desarrolladores. Esto provoca que, generalmente, se obvie esta actividad o se realice un diseño empírico, que no siempre garantiza que se detecten todos los errores relacionados con la lógica interna.

Aparentemente una prueba exhaustiva de caja blanca, produciría programas completamente correctos. No obstante, hasta para pequeños programas, el número de caminos lógicos puede ser enorme. Por esta razón, el desarrollo de una prueba que ejercite exhaustivamente la lógica del programa no es posible ^[4]. Sin embargo, la prueba de caja blanca no se debe descartar. Se pueden elegir y ejercitar una serie de caminos lógicos importantes, comprobar las estructuras de datos fundamentales para verificar su validez, e inclusive, se pueden combinar los atributos de la prueba de caja blanca para llegar a un método que detecte un número considerable de errores relacionados con la lógica interna. Para esto se deberán utilizar técnicas de diseño de casos de prueba, encargadas de seleccionar adecuadamente los valores que permiten que el programa verifique esos escenarios, lo que supone aproximadamente el 40% del costo total de la prueba ^[5]. Por consiguiente, es necesaria, la generación de combinaciones de valores reducidas, a partir de valores interesantes, para los que existen distintas propuestas de algoritmos ^{[6,7,8,9,10,11]}. Es importante, antes de abordar las diferentes técnicas de caja blanca, tener presente la definición del término valor interesante. Un valor interesante es aquel valor que se considere que deba ser utilizado para los casos de prueba, por ser capaz de ejercitar regiones del código y detectar fallas^[12].

Entre las técnicas de prueba de caja blanca se encuentran la prueba de Camino básico y las pruebas de las estructuras de control, esta última compuesta por: la prueba de Bucles, la prueba de Condiciones y la prueba de Flujo de datos ^[2]. Estas técnicas de manera independiente no abarcan escenarios equivalentes y tampoco todos los posibles; por lo que en la literatura se recomienda su adecuada combinación para lograr una mayor detección de los errores del software ^[2,13]. A continuación, se detallan las técnicas de Condiciones y Bucles, que serán las utilizadas en este trabajo.

La prueba de Condiciones ejercita las condiciones lógicas incluidas en un módulo del programa, concentrándose en la prueba de cada condición del programa, para asegurar que no contiene errores ^[14]. Existen dos tipos de condiciones: la condición simple es una variable booleana o una expresión relacional y la condición compuesta está formada por dos o más condiciones simples, operadores lógicos y paréntesis. Para probar una condición es necesario presentar un número suficiente de casos de prueba para demostrar que al menos una vez, se alcanzaron todos los resultados posibles. Se debe ser cuidadoso con la elección de los casos de prueba debido a que, aunque se garantice la ejecución de las condiciones puede ocurrir que alguna cláusula de la decisión no sea ejecutada. Si una condición es incorrecta, entonces es incorrecto al menos un componente de la condición ^[2].

Seguidamente se exponen los tipos de errores frecuentes en una condición:

• Error en operador lógico: debido a que el operador lógico hace que se ejecute siempre la misma rama de la condición.

• Error en variable lógica: debido a que la variable lógica tiene un valor constante antes de ser evaluada.

• Error en paréntesis lógico: debido a que el paréntesis ha agrupado a las operaciones incorrectas.

• Error en operador relacional: debido a que el operador relacional hace que solo se ejecute la misma rama de la condición.

• Error en expresión aritmética: debido a que el valor de la expresión aritmética hace que se ejecute siempre la misma rama de la condición.

En Pressman, R (2010) se proponen una serie de estrategias de prueba de Condiciones para detectar la mayor cantidad de errores explicados anteriormente, algunas de ellas se expondrán a continuación^[2]:

• Prueba de ramificaciones: para una condición compuesta C, es necesario ejecutar al menos una vez las ramas verdaderas y falsas de C y cada condición simple de C ^[4].

• Prueba del dominio: para una expresión relacional de la forma E1, <operador-relacional>E2, se requieren tres pruebas, para comprobar que el valor de E1, es mayor, igual o menor que el valor de E2, respectivamente.

Si el <operador-relacional> es incorrecto y E1, y E2, son correctos, entonces estas tres pruebas garantizan la detección de un error del operador relacional.

Para detectar errores en E1, y E2, la prueba que haga el valor de E1, mayor o menor que el de E2, debe hacer que la diferencia entre estos dos valores sea lo más pequeña posible.

Para una expresión lógica con n variables, habrá que realizar las 2n pruebas posibles (n > 0). Esta estrategia puede detectar errores de un operador, de una variable y de un paréntesis lógico, pero sólo es práctica cuando el valor de n es pequeño.

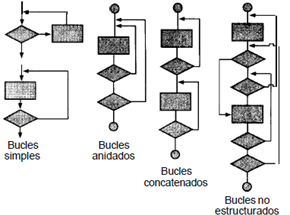
La prueba de Bucles se centra exclusivamente en la validez de las construcciones de bucles. Como se observa en la Figura 1 se pueden definir cuatro clases diferentes de bucles: simples, concatenados, anidados y no estructurados ^[2,13]. Los fallos en un bucle suelen existir en su condición de salida, esta condición, que puede provocar que el bucle se ejecute una vez más o una vez menos de lo esperado, por tanto es importante que sea muy bien analizada ^[2].

Figura 1 Tipos de bucles, tomado de ^[2]. 

Mediante la técnica de bucles se pueden detectar los siguientes errores que se refieren a la ocurrencia de lazos infinitos en el código:

• Terminación de bucles inexistente.

• Variables de bucles modificadas de forma inapropiada.

• Fallo en la salida del bucle cuando se encuentra una iteración divergente.

De acuerdo con Pressman, R (2010) a los bucles simples se les debe aplicar el siguiente conjunto de pruebas, donde n es el número máximo de pasos permitidos por el bucle ^[2]:

• Pasar por alto totalmente el bucle.

• Pasar una sola vez por el bucle.

• Pasar dos veces por el bucle.

• Hacer m pasos por el bucle con m < n.

• Hacer n-1, n y n+1 pasos por el bucle.

Para el tipo de bucle anidado el número de posibles pruebas aumenta geométricamente a medida que aumenta el nivel de anidamiento, lo que llevaría a un número impracticable de pruebas. En Beizer, B (2003) sugiere un enfoque que ayuda a reducir el número de pruebas ^[13]:

• Comenzar por el bucle más interno. Establecer o configurar los demás bucles con sus valores mínimos.

• Llevar a cabo las pruebas de bucles simples para el bucle más interno, mientras se mantienen los parámetros de iteración (por ejemplo, contador del bucle) de los bucles externos en sus valores mínimos.

• Progresar hacia fuera, probar el siguiente bucle, manteniendo los bucles externos en sus valores mínimos y los demás bucles anidados en sus valores típicos (aquellos que permiten que se ejecute el bucle exterior).

• Continuar hasta que se hayan probado todos los bucles.

Los bucles concatenados se pueden probar mediante el enfoque anteriormente definido para los bucles simples, mientras cada uno de los bucles sea independiente del resto. Sin embargo, si hay dos bucles concatenados y se usa el controlador del bucle 1 como valor inicial del bucle 2, entonces los bucles no son independientes. Cuando los bucles no son independientes, se recomienda usar el enfoque aplicado para los bucles anidados ^[2].

En el caso de los bucles estructurados en la literatura se recomienda que sean rediseñados, siempre que sea posible, para que se ajusten a las construcciones de la programación estructurada ^[2].

El requisito básico para realizar pruebas de software automáticas es la generación automática de datos de prueba. Sin embargo, es una tarea muy difícil, ya que un buen conjunto de datos no sólo debe cumplir con todos los requisitos definidos por un criterio de prueba, sino también ser lo más pequeño posible, lo que reduce el costo de la prueba del software ^[5,7]. Como resultado, en los últimos años se ha empleado un mayor esfuerzo en la investigación referente a la generación de datos de prueba de software ^{[6,7,9,10,11,15]}. Como este proceso puede ser visto como un problema de búsqueda, se aborda dentro de la temática de generación de datos de prueba de software basada en búsquedas, donde se pueden aplicar técnicas metaheurísticas ^{[16,17,18,19]}.

Con la utilización de las propuestas de generación de datos de prueba de software basada en búsquedas de autores como: Yu, S.; J. Ai y Y. Zhang (2009), Pachauri, A. y G. Srivastava (2013), Jia (2014) Hermadi, I.; C. Lokan y R. Sarker (2014), Macías, A., et al (2016) Larrosa (2018), D.; P. Fernández y M. Delgado(2018)se generan un conjunto de combinaciones de valores a partir de los dominios de las variables de entrada ^{[7,8,20,21,22,23,24]}.Sin embargo, estas propuestas no comprueban si se han ejecutado los valores límites en los operadores relacionales, a pesar de ser estos, propensos a generar errores. Para esto se debe trabajar en propuestas que tengan en cuenta los valores límites a partir de la verificación del código. En la Tabla 1 se observa la comparación de las propuestas presentadas anteriormente, referido al enfoque de pruebas. En Jia, Y.-H., et al.(2014) incluso tomando como punto de partida la condición, se puede concluir que, no se aplican las técnicas de diseño expuestas en Pressman, R (2010) porque se generan valores para que se cumpla o no la condición, por lo que se reduce a una cobertura de los distintos caminos del programa^[2]. En Larrosa, D (2018), aunque se enfoca en la generación de casos de pruebas unitarias, se utiliza para la generación de los valores de prueba las técnicas de caja negras presentes en Macías, A (2016)quedando sin garantizarse la obtención de altos niveles de cobertura de errores^[23,24].

Tabla 1 Comparación de las propuestas de generación de datos de pruebas 

Propuestas	Enfoque de Pruebas	Técnica que utiliza	Ámbito Teórico	Ámbito Productivo	Tipos de Datos
^[^21^]	Caja Blanca	Camino Básico	X		Numéricos
^[^10^]	Caja Blanca	Camino Básico	X		Numéricos
^[^7^]	Caja Blanca	Camino Básico	X		Numéricos
^[^8^]	Caja Blanca	Camino Básico	X		Numéricos
^[^22^]	Caja Negra			X	Numéricos
^[^20^]	Caja Negra			X	Numéricos, Lógicos y Cadenas
^[^24^]	Caja Blanca	Camino Básico		X	Numéricos, Lógicos y Cadenas

Como indica la Tabla 1 la técnica de diseño de pruebas unitarias que se utiliza en estas propuestas es la del Camino básico, por tanto, con ellas se pueden detectar omisiones en el código y sentencias que no serán ejecutadas. No obstante, omiten errores de gran importancia, como los mencionados anteriormente, asociados a las estructuras de control: bucles y condiciones.

Se puede concluir que: las propuestas existentes en la bibliografía, son validadas con algoritmos específicos, y hasta donde está reportado utilizan datos numéricos únicamente, lo que limita la aplicación de estas propuestas en entornos reales de producción. No aparecen reportes de su introducción en entornos productivos, ni en aplicaciones comerciales, utilizan la técnica del Camino básico y los criterios de cobertura referidos al cubrimiento de caminos, por lo que pueden dejar valores interesantes fuera y con ellos diferentes tipos de errores. Puede ocurrir que al partir del espacio de búsqueda completo se generen algunos de los valores interesantes, pero de forma aleatoria y no intencional a partir del propio diseño del caso de prueba. Por este motivo no asegura la detección de los errores expuestos inicialmente, además, al tomar como punto de partida los dominios continuos para las variables, el conjunto de combinaciones de valores sigue sin reducirse significativamente.

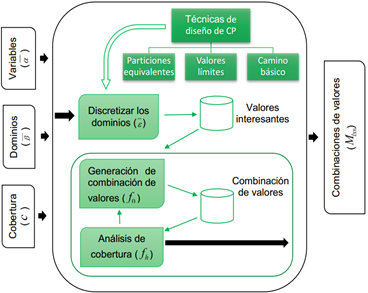
El Grupo de Calidad de Software de la Universidad Tecnológica de La Habana, “José Antonio Echeverría”, CUJAE; trabaja hace varios años en el tema y en particular en las actividades relacionadas con las pruebas de software ^{[25,26,27,28,29]}.Dicho grupo ha definido un modelo para la generación de casos de prueba a partir de diferentes entradas y que genera código de pruebas en diferentes lenguajes ^[23,24]. Los modelos de optimización implementados y las diferentes funciones de transformación para pruebas funcionales se describen en ^[20,30].En Fernández (2016)se define un modelo de optimización para la reducción de combinaciones de valores de pruebas unitarias, expuesto gráficamente en la Figura 2; y del cual se han automatizado un conjunto de procesos que se encuentran dentro del Componente para la Generación de Casos de Pruebas Unitarias (GeCaP) ^[24]. En este trabajo se expone como uno de sus aportes fundamentales la reducción de los dominios de las variables de entrada a partir de la aplicación de técnicas de diseño de valores de prueba para determinar valores interesantes. Para ello se utiliza el vector $\overline{\epsilon }=(e_1,e_2\mathrm{,...,}{e}_k)$ que contiene las transformaciones a emplear para hacer discretos los dominios descritos en $\overline{\beta }$ , que están sustentadas en técnicas de diseño de valores de casos de prueba para cada dominio diferente. De esta forma, los algoritmos heurísticos presentados en Fernández (2016) combinan solo valores interesantes, por lo que se reduce significativamente el espacio de búsqueda y con ello la cantidad de combinaciones generadas para ejecutar los casos de prueba ^[31].En esta propuesta solo se han considerado valores interesantes a partir de los dominios de entrada de cada variable, pero no se ha tenido en cuenta la estructura interna del código para la obtención de valores interesantes, por lo cual se obvian errores detectables a través del análisis de la lógica interna. En el artículo se reconoce este aspecto como una debilidad de la implementación del modelo y se recomienda su incorporación, en trabajos futuros, haciendo uso de técnicas como las de Condiciones y Bucles. Teniendo en cuenta lo anteriormente expuesto, este trabajo tiene como objetivo realizar una propuesta de generación de valores interesantes de forma automática para pruebas unitarias, utilizando las técnicas de diseño de Bucles y Condiciones y abarcando, inicialmente, los tipos de datos numéricos, lógicos y cadenas.

Fig. 2 Modelo para la generación automática de combinaciones de valores de pruebas unitarias ^[32] 

II. MÉTODOS

Para incorporar las técnicas de Condiciones y Bucles a la implementación del vector de transformaciones de los dominios presentado como parte del modelo de optimización descrito anteriormente. Se propone en este trabajo, un conjunto de transformaciones a realizar en el dominio de las variables de entrada, que están determinados por el procesamiento que se realiza de los bucles y las condiciones contenidas en el código que se desea probar. En las tablas 2 y 3 se muestran para cada dominio de entrada la descripción del vector de transformaciones de los dominios $\overline{\epsilon }=\left(e_1,e_2\mathrm{,...,}{e}_k\right)$ y el proceso de obtención del valor, a partir de la aplicación de la técnica concreta (Condiciones o Bucles). Esta información se presenta para los tipos de datos: numérico, lógico y cadena, estableciendo de esta forma la relación entre los datos de entrada a la prueba unitaria y los tipos de errores que pueden ser detectados con las técnicas de Bucles y Condiciones, así como la forma en que se generan.

Los vectores de transformaciones de dominios $\overline{\epsilon }=\left(e_1,e_2\mathrm{,...,}{e}_k\right)$ siguen estas funciones para cada condición, de las estructuras condicionales y bucles, presente en las ecuaciones 1 y 2:

$f_d\left(V_i,Con{d}_k\right)=f_{jt}{}^{-1}\left(V_i,Con{d}_k\right)$ (1)

$f_{jt}{}^{-1}\left(V_i,Con{d}_k\right)=f_{jt}{}^{-1}\left(V_i,f_{j-1t}{}^{-1}\left(V_i,Con{d}_k\right)\right)$ (2)

A continuación, se exponen las inversas de las operaciones $f_{jt}{}^{-1}\left(V_i,Con{d}_k\right)$ para el dominio numérico, de las ecuaciones 3 y 4:

$f_{jt}{}^{-1}\left(V_i,f_{j-1t}{}^{-1}\left(V_i,Con{d}_k\right)\right)=\{\begin{array}{l}{f}_{add}{}^{-1}\left(op,V_i,Sen{t}_l,f_{j-1t}{}^{-1}\left(V_i,Con{d}_k\right)\right)\text{si}\text{op}\in \left\{+\text{, -}\right\}\\ f_{prod}{}^{-1}\left(op,V_i,Sen{t}_l,f_{j-1t}{}^{-1}\left(V_i,Con{d}_k\right)\right)\text{si}\text{op}\in \left\{\times \text{,}÷\right\}\\ f_{sig}{}^{-1}\left(op,V_i,Sen{t}_l,f_{j-1t}{}^{-1}\left(V_i,Con{d}_k\right)\right)\text{si}\text{op}\in \left\{sig\right\}\end{array}$ (3)

$f_{0t}{}^{-1}\left(V_i,Con{d}_k\right)=desp\left(V_i,Con{d}_k\right)$ (4)

Donde:

$V_i\to$ es la variable a procesar.

$o{p}_{}\to$ es el operador que indica la operación a realizar.

$Con{d}_k\to$ es la condición que se está analizando y que debe condicionar el valor de entrada de la variable $V_i$ .

$f_d\to$ es la función de obtención de un valor interesante para la variable $V_i$ .

$f_{j{t}^{}}{}^{-1}\to$ es la función de transformación inversa de $V_i$ en el código, es decir, es una función que permite obtener un valor resultante de aplicar $n$ transformaciones inversas a la variable de entrada de forma tal que se evalúan los valores interesantes de la condición en la prueba unitaria, con $n$ que representa la cantidad de transformaciones que sufre la variable.

$Sen{t}_l\to$ es una sentencia dentro del código, $l$ va desde 1 hasta la cantidad de sentencias que tenga el código.

Para el caso del dominio cadena la función inversa se describe a continuación, en la ecuación 5:

$f_{jt}{}^{-1}\left(V_i,f_{j-1t}{}^{-1}\left(V_i,Con{d}_k\right)\right)=\{\begin{array}{l}\text{si}\text{op}\in \left\{\subseteq \text{,}\supseteq \right\}\\ f_{subset}{}^{-1}\left(op,V_i,startpos,endpos,Sen{t}_l,f_{j-1t}{}^{-1}\left(V_i,Con{d}_k\right)\right)\\ \text{si}\text{op}=\text{replace}\\ f_{replace}{}^{-1}\left(V_i,sourItem,tarItem,Sen{t}_l,f_{j-1t}{}^{-1}\left(V_i,Con{d}_k\right)\right)\\ \text{si}\text{op}\in \left\{\cup ,split\right\}\\ f_{union}{}^{-1}\left(op,V_i,splitItem,Sen{t}_l,f_{j-1t}{}^{-1}\left(V_i,Con{d}_k\right)\right)\end{array}$ (5)

Tabla 2 Relación entre tipos de datos de entrada y errores detectados con la técnica de Condiciones 

Dominios	Vector de transformación de dominios $\overline{\epsilon }=\left(e_1,e_2\mathrm{,...,}{e}_k\right)$	Obtención de valores interesantes a partir de valores de entrada y estructura interna
Numérico	Valor límite de la condición.	$e_1\left(V_i,D\right)=f_d\left(V_i,Con{d}_k\right)$
	Valor que cumple la condición, diferente del valor límite.	Si el operador relacional es < o <= el valor es: $e_2\left(V_i,D\right)=f_d\left(V_i,add\left(Con{d}_k,-1\right)\right)$ Si el operador relacional es > o >= el valor es: $e_2\left(V_i,D\right)=f_d\left(V_i,add\left(Con{d}_k\mathrm{,1}\right)\right)$
	Valor que no cumple la condición, diferente del valor límite.	Si el operador relacional es < o <= el valor es: $e_3\left(V_i,D\right)=f_d\left(V_i,add\left(Con{d}_k\mathrm{,1}\right)\right)$ Si el operador relacional es > o >= el valor es: $e_3\left(V_i,D\right)=f_d\left(V_i,add\left(Con{d}_k,-1\right)\right)$
Lógico	Valor que cumple la condición.	El vector de transformaciones de los dominios $\overline{\epsilon }=\left(e_1,e_2\mathrm{,...,}{e}_k\right)$ para las variables lógicas se reduce a generar valores verdaderos y falsos para probar la condición.
	Valor que no cumple la condición.
Cadena	Valor que cumple la condición.	Para los distintos operadores contenidos en el conjunto $\text{{}\subseteq ,\supseteq ,\cup ,\varnothing ,=\}$ el vector de transformaciones de los dominios genera los siguientes valores: $e_1\left(V_i,D\right)=f_d\left(V_i,Con{d}_k\right)$
	Valor que no cumple la condición.	$e_2\left(V_i,D\right)=f_d\left(V_i,NOT(Con{d}_k)\right)$

De forma similar, se obtienen los valores interesantes al aplicar la técnica de Bucles. La implementación propia de esta técnica para los vectores de transformación de los dominios se detalla en la Tabla 3. Para su comprensión se define la ecuación 6 y se especifica los términos que utiliza:

$f_d\left(V_i,Bucl{e}_k\right)=f_{jt}{}^{-1}\left(V_i,Bucl{e}_k\right)$ (6)

$Bucl{e}_k\to$ es la condición del bucle que se está analizando y que condiciona el valor de entrada de la variable $V_i$ .

$inc\to$ es la transformación realizada a la variable de control.

$opInc\to$ operador de $inc$ .

$n\to$ cantidad de pasos permitidos por el bucle.

Tabla 3 Relación entre tipos de datos de entrada y errores detectados con la técnica de Bucles 

Dominios	Vector de transformación de dominios $\overline{\epsilon }=\left(e_1,e_2\mathrm{,...,}{e}_k\right)$	Obtención de valores interesantes a partir de valores de entrada y estructura interna
Numérico	Valor para pasar por alto el bucle	Si el operador relacional es < o > el valor es: $e_1\left(V_i,D\right)=f_d\left(V_i,Bucl{e}_k\right)$ Si el operador relacional es <= o >= el valor es: Si $\text{opInc}\in \left\{+\text{, -}\right\}$ : $e_1\left(V_i,D\right)=f_d\left(V_i,add\left(Bucl{e}_k,inc\right)\right)$ Si $\text{opInc}\in \left\{\times \text{,}÷\right\}$ : $e_1\left(V_i,D\right)=f_d\left(V_i,prod\left(Bucl{e}_k,inc\right)\right)$
	Valor para pasar 1 vez por el bucle	Si el operador relacional es < o > el valor es: Si $\text{opInc}\in \left\{+\text{, -}\right\}$ : $e_2\left(V_i,D\right)=f_d\left(V_i,add\left(Bucl{e}_k,inc\right)\right)$ Si $\text{opInc}\in \left\{\times \text{,}÷\right\}$ : $e_2\left(V_i,D\right)=f_d\left(V_i,prod\left(Bucl{e}_k,inc\right)\right)$ Si el operador relacional es <= o >= el valor es: $e_2\left(V_i,D\right)=f_d\left(V_i,Bucl{e}_k\right)$
	Valor para pasar n-1 veces por el bucle	Si el operador relacional es < o > el valor es: Si $\text{opInc}\in \left\{+\text{, -}\right\}$ : $e_3\left(V_i,D\right)=f_d\left(V_i,add\left(Bucl{e}_k,inc*(n-1)\right)\right)$ Si $\text{opInc}\in \left\{x\text{,}÷\right\}$ : $e_3\left(V_i,D\right)=f_d\left(V_i,prod\left(Bucl{e}_k,inc*(n-1)\right)\right)$ Si el operador relacional es <= o >= el valor es: Si $\text{opInc}\in \left\{+\text{, -}\right\}$ : $e_3\left(V_i,D\right)=f_d\left(V_i,add\left(Bucl{e}_k,inc*(n-2)\right)\right)$ Si $\text{opInc}\in \left\{x\text{,}÷\right\}$ : $e_3\left(V_i,D\right)=f_d\left(V_i,prod\left(Bucl{e}_k,inc*(n-2)\right)\right)$
	Valor para pasar n veces por el bucle	Si el operador relacional es < o > el valor es: Si $\text{opInc}\in \left\{+\text{, -}\right\}$ : $e_4\left(V_i,D\right)=f_d\left(V_i,add\left(Bucl{e}_k,inc*n\right)\right)$ Si $\text{opInc}\in \left\{x\text{,}÷\right\}$ : $e_4\left(V_i,D\right)=f_d\left(V_i,prod\left(Bucl{e}_k,inc*n\right)\right)$ Si el operador relacional es <= o >= el valor es: Si $\text{opInc}\in \left\{+\text{, -}\right\}$ : $e_4\left(V_i,D\right)=f_d\left(V_i,add\left(Bucl{e}_k,inc*(n-1)\right)\right)$ Si $\text{opInc}\in \left\{x\text{,}÷\right\}$ : $e_4\left(V_i,D\right)=f_d\left(V_i,prod\left(Bucl{e}_k,inc*(n-1)\right)\right)$
	Valor para pasar n+1 veces por el bucle	Si el operador relacional es < o > el valor es: Si $\text{opInc}\in \left\{+\text{, -}\right\}$ : $e_5\left(V_i,D\right)=f_d\left(V_i,add\left(Bucl{e}_k,inc*(n+1)\right)\right)$ Si $\text{opInc}\in \left\{x\text{,}÷\right\}$ : $e_5\left(V_i,D\right)=f_d\left(V_i,prod\left(Bucl{e}_k,inc*(n+1)\right)\right)$ Si el operador relacional es <= o >= el valor es: Si $\text{opInc}\in \left\{+\text{, -}\right\}$ : $e_5\left(V_i,D\right)=f_d\left(V_i,add\left(Bucl{e}_k,inc*n\right)\right)$ Si $\text{opInc}\in \left\{x\text{,}÷\right\}$ : $e_5\left(V_i,D\right)=f_d\left(V_i,prod\left(Bucl{e}_k,inc*n\right)\right)$

Con la obtención de estos valores se garantiza la cobertura de los errores, descritos anteriormente, que pueden ser detectados con las técnicas de Bucles y Condiciones. Se destaca que, como parte del análisis de la estructura interna y con el objetivo de aplicar estas técnicas de diseño de casos de prueba, se detectan un grupo de posibles errores y advertencias que son reportadas como salidas de los algoritmos implementados y que pueden ser de mucha utilidad. Estas serían propuestas de errores potenciales, basados en los errores expuestos, que tiene el código que se pretende probar; sus descripciones se presentan en la Tabla 4.

Tabla 4 Errores detectados con la propuesta durante el análisis de la lógica interna. 

Tipo de error o advertencia	Descripción
Variables de bucles modificadas de forma inapropiada.	La variable de control del bucle se modifica de forma inapropiada con respecto al operador de la condición.
Variables no influyen en la condición.	No se pueden generar valores para variables iguales en ambos miembros de la condición, debido a que se anulan.
Variable de control errónea o no se modifica dentro del bucle.	La variable de control seleccionada para el bucle no es correcta o no se le realizan cambios dentro del bucle.
Condición errónea	No se pueden generar valores porque la condición nunca se cumple.
Variable de control errónea o no está contenida en la condición.	La variable de control seleccionada para el bucle no es correcta o no se encuentra contenida en la condición del bucle.
Variable no inicializada	La variable contenida en la condición no ha sido inicializada.
El bucle no posee una condición controladora.	El bucle no posee una variable que controle cada iteración.
Condición constante.	No se pueden generar valores porque las variables que intervienen en la condición poseen valores constantes.
Variable divergente no se modifica en el interior del bucle	Las variables divergentes no influyen en la iteración del bucle.

III. RESULTADOS

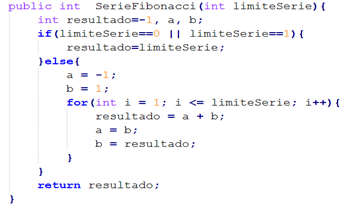
El generador de valores interesantes se integró con GeCaP, que utiliza la descripción del dominio de las variables para la generación de valores, con el objetivo de realizar una comparación entre la cantidad de errores detectados antes y después de la integración. En la figura 3 se observa el algoritmo de la serie Fibonacci, el cual es utilizado para la comparación, donde el intervalo de valores a utilizar para la variable de entrada limite Serie es [0,20]. En la tabla 5 se muestran los resultados obtenidos.

Fig. 3 Serie Fibonacci 

Tabla 5 Análisis de los resultados obtenidos en las ejecuciones antes y después de la integración 

Camino	Generación de valores con GeCaP					Generación de valores con GeCaP + Generador de valores interesantes para CPU
	Ej. 1	Ej. 2	Ej. 3	Ej. 4	Ej. 5	Ej. 1	Ej. 2	Ej. 3	Ej. 4	Ej. 5
T, -, -	0	0	0	0	0	0	0	0	0	0
F, T, -	-	-	-	-	-	1	1	1	1	1
F, F, T	20	21	20	20	-1	8	4	9	2	2
F, F, F	-1	20	20	20	-1	-1	-1	-1	-1	-1
% de cobertura de errores	45%	45%	36%	36%	36%	72%	72%	72%	81%	81%

IV. DISCUSIÓN

En la Tabla 5 se muestra la ejecución del componente GeCaP, a partir de los valores generados. Como se puede observar, en todas las ejecuciones se generan combinaciones de valores para tres, de los cuatro caminos independientes. Esto se debe a que, para el ejemplo objeto de análisis, no se puede generar el valor 1 de la variable limiteSerie a partir de la técnica empleada. Sin embargo, este valor constituye un valor límite obtenido a partir de la comprensión de la lógica interna del método; lo que provoca que la condición limiteSerie==1 no se satisfaga y tampoco lo haga el camino “F, T, -”.

En la propia tabla se expone adicionalmente, una ejecución del componente GeCaP a partir de la integración con la propuesta. Como se puede observar, en esta ejecución se han podido satisfacer los cuatro caminos y en particular las condiciones que los determinan.

Luego de analizar los resultados obtenidos en las ejecuciones realizadas, se evidencia que la descripción del dominio de las variables no garantiza generar valores interesantes para cubrir los caminos. Se debe tener en cuenta también la estructura interna del código para generar dichos valores, pues en las ejecuciones realizadas se queda un camino sin satisfacer (F, T, -). No sucediendo así con el uso de las técnicas de Condiciones y Bucles presentes en el generador que tienen presente la lógica interna, lo que evidencia el valor práctico de la propuesta.

Si se analizan los valores generados en el caso de la propuesta se puede comprobar que en las ejecuciones se alcanzó un nivel de cobertura de los bucles y condiciones que en ningún caso llegó al 100%, esto se debe a que las funciones objetivo y heurísticas que utiliza GeCaP, solo considera criterios de cobertura de caminos y no tiene en cuenta la cobertura de bucles y condiciones.

V. CONCLUSIONES

1. A partir del análisis de la lógica interna, se logró realizar una propuesta de valores interesantes de forma automática; para los tipos de datos: numéricos, lógicos y cadenas, utilizando las técnicas Bucles y Condiciones. No obstante, se puede concluir que, a pesar de que se generaron valores para obtener el 100% de cobertura de decisiones, no fue posible conseguirlo.

2. Para trabajos futuros se deben integrar en la función objetivo los aportes que pueden hacer las técnicas de Bucles y Condiciones para alcanzar mayores niveles de cobertura.

VI. REFERENCIAS

1.  Ali S, Briand LC, Hemmati H, et al. A systematic review of the application and empirical investigation of search-based test case generation. IEEE Transactions on Software Engineering. 2010;36(6):742-62. ISSN 0098-5589.

2.  Anielak G, Jakacki G, Lasota S. Incremental test case generation using bounded model checking: an application to automatic rating. International Journal on Software Tools for Technology Transfer. 2015;17(3):339-49. ISSN 1433-2779.

3.  Beizer B. Software testing techniques: Dreamtech Press; 2003. ISBN 8177222600.

4.  Bueno PM, Jino M, Wong WE. Diversity oriented test data generation using metaheuristic search techniques. Information Sciences, Elsevier. 2014;259:490-509. ISSN 0020-0255.

5.  Delgado MD, Macías A, Larrosa D, et al. Model for Automatic Generation of Search-Based Early Tests. Computación y Sistemas. 2017;21(3). ISSN 2007-9737.

6.  Delgado MD, Verona S, Fernández PB, et al. Calculation of priorities of test cases from the functional requirements. Revista Cubana de Ciencias Informáticas. 2016;10. ISSN 1994-1536.

7.  Fernández PB. Modelo para la generación automática de combinaciones de valores de pruebas unitarias [Tesis de Maestría]: Instituto Superior Politécnico: José Antonio Echeverría; 2016.

8.  Fernández PB, Cantillo W, Delgado MD, et al. Generación de combinaciones de valores de pruebas utilizando metaheurística/Generating combinations of test values using metaheuristics. Ingeniería Industrial. 2016;37(2):200-7. ISSN 1815-5936.

9.  Grindal M, Offutt J, Andler SF. Combination testing strategies: a survey. Software testing, Verification and reliability, Wiley. 2005;15(3):167-99. ISSN 1099-1689.

10.  Harman, Mansouri. Search based software engineering: introduction to the special issue. IEEE Transactions on Software Engineering. 2010;36(6):737-41. ISSN 1939-3520.

11.  Harman Mark, Phil M. A theoretical and empirical study of search-based testing: Local, global, and hybrid search. IEEE Transactions on Software Engineering . 2010;36(2):226-47. ISSN 0098-5589.

12.  Hermadi I, Lokan C, Sarker R. Dynamic stopping criteria for search-based test data generation for path testing. Information and Software Technology, Elsevier. 2014;56(4):395-407. ISSN 0950-5849.

13.  Jia Y-H, Chen W-N, Zhang J, et al. Generating Software Test Data by Particle Swarm Optimization. En: Simulated Evolution and Learning. Springer; 2014. p. 37-47. ISBN 3319135627.

14.  Jústiz D, Gómez D, Delgado MD. Proceso de pruebas para productos de software en un laboratorio de calidad. Ingeniería Industrial . 2014;35(2):131-45. ISSN 1815-5936.

15.  Larrosa D, Fernández P, Delgado M. GeCaP: Generador de casos de pruebas unitarias a partir del código fuente en lenguaje Java. Polibits. 2018;57:67-73. ISSN 2395-8618.

16.  Macías A, Delgado MD, Fajardo J, et al. Generación automática de combinaciones de valores para pruebas funcionales utilizando metaheurísticas. Ingeniería Industrial . 2016;7(2):48-54. ISSN 2223-1781.

17.  Macías A, Delgado MD, Fajardo J, et al. Generador de valores de casos de prueba funcionales. Lámpsakos. 2016 (15):51-8. ISSN 2145-4086.

18.  Mann M, Tomar P, Sangwan OP. Bio-inspired metaheuristics: evolving and prioritizing software test data. Applied Intelligence. 2018;48(3):687-702. ISSN 0924-669X.

19.  Mao C. Harmony search-based test data generation for branch coverage in software structural testing. Neural Computing & Applications, Springer. 2014;25(1):199-216. ISSN 0941-0643. DOI 10.1007/s00521-013-1474-z.

20.  Mao C, Xiao L, Yu X, et al. Adapting ant colony optimization to generate test data for software structural testing. Swarm and Evolutionary Computation, Elsevier. 2015;20:23-36. ISSN 2210-6502.

21.  Myers GJ, Sandler C, Badgett T. The art of software testing. 3rd ed ed. EUA: John Wiley & Sons; 2011. ISBN 97811118133156.

22.  Pachauri A, Srivastava G. Automated test data generation for branch testing using genetic algorithm: An improved approach using branch ordering, memory and elitism. Journal of Systems and Software, Elsevier. 2013;86(5):1191-208. ISSN 0164-1212.

23.  Pressman R. Ingeniería del Software: Un enfoque práctico. 7th ed. ed. México D.F: McGraw-Hill; 2010. ISBN 9786071503145.

24.  Tai K. What to do beyond branch testing. ACM SIGSOFT Software Engineering Notes, ACM Digital Library. 1989;14(2):58-61. ISSN 0163-5948.

25.  Tenorio RR. Las pruebas de software y su importancia en las organizaciones [Tesis Doctoral]. México, Veracruz: Universidad Veracruzana; 2010.

26.  Torres E, Delgado MD, Lodos J, et al. Process for Unattended Execution of Test Components. Polibits. 2014 (49):5-17. ISSN 1870-9044.

27.  Torres L, Delgado MD, Rodríguez D, et al. Entorno de ingeniería de requisitos aplicado para producir software en una universidad. Ingeniería Industrial . 2014;35(1):45-59. ISSN 1815-5936.

28.  Valdéz CJLC. Implementación del modelo integral colaborativo (MDSIC) como fuente de innovación para el desarrollo ágil de software en las empresas de la zona centro - occidente en México. [Doctorado en planeación estratégica y dirección de tecnología.]. México: Universidad Popular Autónoma del Estado de Puebla; 2014.

29.  Verona S, Pérez Y, Torres L, et al. Pruebas de rendimiento a componentes de software utilizando programación orientada a aspectos. Ingeniería Industrial . 2016;37(3):278-85. ISSN 1815-5936.

30.  Xianbin Feng, Rui D, Yan Z, et al. An Advanced Genetic Algorithm Apply to Test Data Generation for Paths Coverage. Applied Mechanics & Materials. 2014;602:3347-50. ISSN 1662-7482. DOI 10.4028/www.scientific.net/AMM.602-605.3347.

31.  Xiao M, El-Attar M, Reformat M, et al. Empirical evaluation of optimization algorithms when used in goal-oriented automated test data generation techniques. Empirical Software Engineering, Springer. 2007;12(2):183-239. ISSN 1382-3256.

32.  Yu S, Ai J, Zhang Y. Software test data generation based on multi-agent. Advances in Software Engineering, Elsevier. 2009:188-95. ISSN 3642106188.

Recibido: 23 de Marzo de 2018; Aprobado: 08 de Enero de 2019