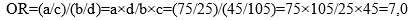Introducción
En diferentes ámbitos de la investigación científica, ya sea en estudios epidemiológicos en poblaciones o en el área clínica, es muy común que los investigadores pretendan buscar factores de riesgo o pronósticos. Existen medidas de la fuerza de asociación entre dos variables las cuales permiten estimar los mencionados factores. De manera general se tiene una variable dependiente (cualquier evento ya sea una enfermedad, complicación, muerte, entre otros), y otra u otras independientes que serían los factores de riesgo o pronóstico a los que está expuesta determinada persona para que ocurra el evento en cuestión. Las medidas de la fuerza de asociación más utilizadas son el riesgo relativo (RR) y el odss ratio (OR).
¿Cuándo utilizar OR o RR para medir la fuerza de asociación?
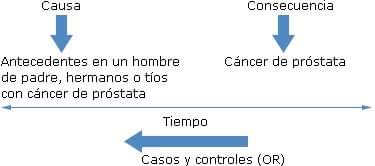
Todo depende del tipo de diseño de la investigación y el análisis estadístico que se va a realizar. Supongamos que se tiene una causa y un efecto, por ejemplo, antecedentes en un hombre con cáncer de próstata (efecto), de padre, hermanos o tíos con dicha enfermedad (causa). Hay una opción, buscar quiénes enfermaron de cáncer de próstata (casos) y seleccionar otro grupo de hombres sin la enfermedad (controles), entonces compararlos, según la presencia o no de los antecedentes antes referidos. Este diseño es un estudio analítico, retrospectivo de casos y controles1,2,3 (fig. 1).
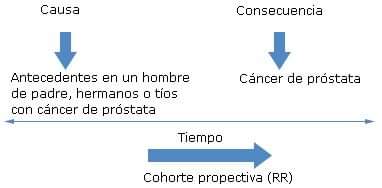
Por el contrario, en el mismo ejemplo, se pude empezar viendo qué hombres tienen los antecedentes ya descritos y seguirlos en el tiempo para ver los que enferman de cáncer de próstata. Este diseño es analítico de cohorte (para diferenciar de los de corte o transversales prospectiva) y la forma de medir el riesgo es el RR1,2,3,4 (fig. 2).
Antes de definir qué es RR se debe hacer alusión a algunas medidas estadísticas:
Cociente: un número dividido por otro (a/x).
Proporción: un cociente donde el numerador a está contenido en el denominador a+b y no tiene unidades de medida.
Razón: el numerador a no está contenido en el denominador b ; puede tener unidades de medida.
Tasa: constituye una medida de la frecuencia de un fenómeno. En epidemiología, demografía y estadísticas vitales, la tasa es una expresión de la frecuencia con que ocurre un hecho en una población determinada expuesta a riesgo. Una tasa se compondrá de: un numerador (lo que se quiere medir), un denominador (una población), un tiempo específico en el que ocurren los hechos y un coeficiente múltiplo de 10 con el que se multiplica el resultado para que se obtengan números enteros.
Riesgo: probabilidad de que ocurra un evento.
Probabilidad: es simplemente en términos comunes el cociente entre lo que ocurre y lo que puede ocurrir (ocurre/puede ocurrir), por ejemplo, lanzar una moneda al suelo implica que pueda caer escudo o estrella (dos posibles resultados que pueden ocurrir) y al caer puede obtenerse un solo resultado de estos dos por tanto, sería uno dividido entre dos (escudo o estrella) matemáticamente eso es ½, por tanto, la probabilidad de que al tirar una moneda al piso y se obtenga el resultado de escudo o estrella es de 0,5, pero para entenderlo mejor si multiplicamos por 100 diríamos que es de un 50,0 %. Las probabilidades oscilan en el rango entre 0 y 1, algo que nunca sucede, sería la probabilidad 0 y lo que siempre ocurre 1. La probabilidad de no fallecer en algún momento de la vida sería 0 y la de que ocurra ese evento también en algún momento de la vida es 1, pues siempre que nacemos pues inevitablemente se muere algún día.5
La incidencia es el número de casos nuevos de la enfermedad que se investiga, que aparece en un período de tiempo previamente determinado, mide el riesgo o probabilidad de enfermar. El riesgo en epidemiología es la probabilidad de ocurrencia de un evento, típicamente de enfermar, aunque también de morir, de curación de los individuos.6,7
¿Qué es el riesgo relativo?
El RR es la razón de dos tasas de incidencias, la de los individuos expuestos en los que enferman y la de los no expuestos que también contraen la enfermedad, mide la fuerza de asociación entre la exposición y la enfermedad; cuántas veces es más probable que ocurra el evento en los expuestos en relación a los no expuestos.5,8
Dicho de otra manera, el RR es un cociente de dos probabilidades, la probabilidad de tener la enfermedad en cuestión en los expuestos sobre la probabilidad de no tenerla en los no expuestos. Más comúnmente se expresa como la tasa de incidencia de la enfermedad en expuestos sobre la tasa de incidencia de la enfermedad en los no expuestos (RR=Tasa incidencia en expuestos/Tasa de incidencia en no expuestos).2,3,5,8
Cálculo del riesgo relativo
A partir de un ejemplo se explicará cómo se calcula el RR, supongamos que se tiene un grupo de 153 individuos expuestos al consumo excesivo de bebidas alcohólicas (variable independiente) y 145 no expuestos, los cuales se observan durante un tiempo determinado en el que un grupo enferma de cirrosis hepática (variable dependiente) y otro no, entonces a partir de la siguiente tabla de contingencia estamos en condiciones de hacer el cálculo del riesgo relativo (tabla 1).
Tabla 1 Exposición al alcohol y riesgo de cirrosis hepática
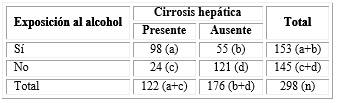
Tasa de incidencia en expuestos (TIE)=a/a+b
Tasa de incidencia en no expuestos (TINE)=c/c+d
RR=TIE/TINE
Antes de estimar el RR se hace necesario realizar una prueba estadística que permita comprobar que existe asociación entre la exposición y la enfermedad, pues no tiene sentido medir la fuerza de asociación, si lo anterior no se cumple, El estadígrafo que se utiliza en este caso es la prueba chi cuadrado ((2) de Pearson de homogeneidad. Se fija un nivel de significación, por lo general 0,05. Si la probabilidad que le corresponde al valor de esa ((2), bajo el supuesto de que se cumple la hipótesis nula, (no hay relación entre la exposición y la enfermedad) es menor que dicha significación, entonces se puede afirmar que hay asociación entre la exposición y la enfermedad por tanto, se puede buscar la fuerza de esa relación.
Según el ejemplo expuesto y con la ayuda del programa estadístico Epidat 3.1, el valor de la (2 con corrección por continuidad sería 67,52 con un valor de p=0,000, es decir, p<0,001, porque la probabilidad de que esos resultados ocurran es muy baja, bajo el supuesto de que se cumpla la hipótesis de que no existe relación entre el consumo excesivo de alcohol y enfermar de cirrosis, es preferible pensar que no se cumple y se puede decir que existe asociación entre dicha exposición y la enfermedad. Debido a este resultado se puede cuantificar la fuerza de esa asociación mediante el RR.
Según el ejemplo anterior el RR sería:
Tasa de incidencia en expuestos (TIE): 98/153=0,64
Tasa de incidencia en expuestos (TINE): 24/145=0,17
RR=TIE/TINE=0,64/0,17=3,76
IC de 95 % (2,63 - 5,68)
Si el RR es mayor que 1 y los valores de los límites inferior o superior del IC de 95 % rebasan la unidad, significa que la TIE es mayor que la TINE, la asociación es positiva o directa, entonces la exposición podría ser un factor de riesgo, como en el ejemplo que se muestra, para enfermar de cirrosis hepática. Si el RR es menor que 1 y los límites inferior y superior de su IC de 95 %, están por debajo de la unidad (no contiene al 1), la TIE es menor que la TINE, la asociación es negativa o inversa, en este caso la exposición sería un factor protector para no tener la enfermedad. Si el límite inferior del IC de 95 % para el RR, es menor que 1 y el superior mayor que dicho valor, se interpreta como que no hay ninguna relación estadísticamente significativa, entre la exposición y la enfermedad o el evento de interés, por ende, no puede descartarse que el valor observado se deba al azar (fig. 3). Como el RR fue igual a 3,76, se interpreta como que es aproximadamente 4 veces más probable enfermar de cirrosis hepática cuando se consume alcohol excesivamente que en el caso contrario.
¿Qué es un odds ratio?
Estas dos palabras han sido traducidas al español como razón (del inglés ratio) de productos cruzados, más adelante se verá por qué se le ha denominado así, razón de ventajas, razón de momios, razón de disparidad, razón de desigualdad y oportunidad relativa.1,2,8,9,10,11,12 El concepto de odds (también llamado momio) se maniobra en el contexto anglosajón, en las apuestas que se hacen en juegos de azar y se trata de un cociente entre la probabilidad de que ocurra un evento determinado y la probabilidad de que no ocurra ese evento [(P(evento)/1-P(evento)]. Un OR es la relación por cociente entre dos odds.12
Cálculo e interpretación de los OR en estudios de casos y controles retrospectivos
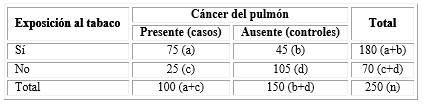
Al igual que se comentó sobre el RR, mediante el siguiente ejemplo se expondrá cómo se realiza el cálculo de los OR en un estudio de casos y controles. Vamos a suponer que se dispone de una muestra de 100 pacientes con cáncer del pulmón (casos) y 150 sin la enfermedad (controles). Se indaga en cada muestra quién consumió tabaco y se confirma que los enfermos fumaban antes de presentar la enfermedad para garantizar la temporalidad (la causa precede al efecto en el tiempo). Los OR también se pueden utilizar en las investigaciones prospectivas y transversales analíticas, pero en estas últimas, solo para medir la fuerza de la asociación y no con la intención de buscar un riesgo porque no tienen en cuenta la temporalidad.
En los estudios de casos y controles la relación que existe dentro de cada columna viene fijada por la frecuencia de la exposición dentro de los casos y dentro los controles, podemos calcular el odds de exposición dentro de los casos (a/c) y el odds de exposición dentro de los controles (b/d), obtenemos dos odds que se pueden relacionar mediante una razón y es a lo que se le denomina razón de odds u odds ratio.
Del total de 100 pacientes que tenían cáncer del pulmón (casos) 75 fumaban y 25 no fumaban, el odds de tener cáncer del pulmón en pacientes fumadores es a/c es decir 75/25=3. En un total de 150 personas que no tienen dicha enfermedad (controles), el odds de no tener cáncer del pulmón en pacientes fumadores es 45/105=0,429, por tanto, el OR sería igual a 3/0,429, este cociente o razón de odds (OR) sería igual a 7,0. Entonces a partir de la siguiente tabla 2 de contingencia se efectuará el cálculo de OR.
Por tanto matemáticamente un OR se representa por la siguiente fórmula:
Es por eso que a los OR se les ha denominado razón de productos cruzados (a×d/b×c). Antes de calcular el OR se procede, como se explicó anteriormente, con el RR. Si la probabilidad que le corresponde al valor de (2 bajo el supuesto de que se cumple la hipótesis nula es menor que dicha significación, entonces se puede afirmar que hay asociación entre la exposición y la enfermedad, por tanto, se puede buscar la fuerza de esa relación. Con la ayuda del programa estadístico Epidat 3.1, el valor de la (2 con corrección por continuidad sería 46,89 con un valor de p=0,000, por tanto, debido a que la probabilidad de que esos resultados ocurran es muy baja, si se cumple la hipótesis de que no existe relación entre el consumo de tabaco y enfermar de cáncer del pulmón, se puede decir que existe asociación entre dicha exposición y la enfermedad. Debido a este resultado se puede cuantificar la fuerza de esa asociación mediante el OR ya calculado (7,0) que su intervalo de confianza de 95 % sería (3,95-12,40).
Si el OR es mayor que 1 y los valores de los límites inferior o superior del IC de 95 % rebasan la unidad, significa que la asociación es positiva o directa, entonces la exposición podría ser un factor de riesgo, como en el ejemplo que se muestra, para enfermar de cáncer del pulmón. Si el OR es menor que 1, y los límites inferior y superior de su IC de 95 %, están por debajo de la unidad (no contiene al 1), la asociación es negativa o inversa, entonces la exposición sería entonces un factor protector para no tener la enfermedad. Si el límite inferior del IC de 95 % para el RR, es menor que 1 y el superior mayor que dicho valor, se interpreta como que no hay ninguna relación estadísticamente significativa, entre la exposición y la enfermedad o el evento de interés, por ende, no puede descartarse que el valor observado se deba al azar (fig. 4). En este ejemplo se interpreta que los sujetos que fuman tienen siete veces mayor chance u oportunidad de enfermar de cáncer del pulmón que los que no fuman.
El OR y RR se igualan cuando la prevalencia de la enfermedad es muy baja, es decir, para enfermedades muy raras o de muy baja frecuencia de presentación.
Este artículo constituirá una vía de aprendizaje para los investigadores en el campo de las ciencias médicas, para determinar cuándo se utilizan, cómo se calculan e interpretan el RR y el OR. Se enfatizó en que el RR y el OR miden la fuerza de asociación y el hecho de que sean significativamente diferentes de uno, no implica que existe una relación de causa y efecto pues tienen que cumplirse los criterios de causalidad expuestos por Bardford-Hill,12 fundamentalmente la temporalidad, la causa precede al efecto en el tiempo.