ARTÍCULO ORIGINAL

Modelo económico matemático para optimizar la ganancia en la empresa Talabartería THABA

 

Economic-Mathematical Model for Optimizing the Profit in Talabartería THABA Company

 

 

Eduardo Martínez Puig

Facultad de Economía, Universidad de La Habana, Cuba.

 

 

---

RESUMEN

Con frecuencia, en el proceso de toma de decisiones en la esfera empresarial, se debe hallar la mejor solución entre un conjunto de alternativas posibles, bajo la problemática común de la escasez de recursos. Los métodos y las técnicas cuantitativas se han convertido en una importante herramienta y, en particular, la programación lineal y en enteros constituye una de las técnicas de la programación matemática más utilizadas. En el presente artículo se determina el plan óptimo de producción trimestral que maximiza la ganancia en la producción de surtidos en la unidad empresarial de base (UEB) 102, perteneciente a la empresa Talabartería THABA. Se construyen modelos de programación lineal y en enteros con condiciones lógicas, y se realiza un análisis de los resultados obtenidos a través del uso del paquete informático denominado "Sistema para el análisis cuantitativo de negocios sobre el ambiente Windows" (WinQSB).

PALABRAS CLAVES: función objetivo, optimización condicionada, programación en enteros, variable auxiliar entera, variables binarias.

---

ABSTRACT

In the decision making process of the enterprise field, and with the purpose of finding the best solution within a set of possible alternatives under the common problematic of resources shortage, the Methods and Quantitative Techniques have become a major tool. Therefore, the methods and quantitative techniques have become an important tool. Specifically, Linear Programming and in Integers is one of the most widely used mathematic programming technique. The present paper delimits the three-months production optimal plan which increases profit in the manufacturing of supplies in UEB 102, Talabartería THABA Company. Linear Programming and in Integers models are developed, and an analysis of outcomes resulting from the usage of WinQSB is carried out.

KEYWORDS: objective function, conditioned optimization, programming in integer numbers, integer auxiliary variable, binary variable.

---

 

 

INTRODUCCIÓN

El proceso de toma de decisiones en los distintos niveles organizacionales es cada vez de mayor complejidad, debido, fundamentalmente, a la creciente escasez y carestía de todo tipo de recursos. La forma actual en que se planifica la producción en la empresa Talabartería THABA -que se encuentra bajo el régimen de perfeccionamiento empresarial- no está soportada sobre bases científicas, lo cual no le permite tomar en cuenta importantes factores relativos a la obtención de ganancia máxima, entre otros elementos importantes de la planificación de sus planes productivos.

Por esta razón, sería conveniente tener el conocimiento de los volúmenes de producción de los diferentes surtidos que elabora la UEB 102, con las limitaciones materiales con que se deben producir los artículos (los insumos fundamentales son importados y se obtienen en divisas), de manera tal que se alcance un nivel máximo de ganancia con la producción. Estos elementos pueden ayudar a que la empresa tenga mejores resultados económicos en su eficiencia y eficacia, aspectos relevantes a tomar en cuenta por toda empresa, especialmente por aquellas que se encuentren en el régimen de perfeccionamiento empresarial. Es por ello que este artículo tiene como objetivo general determinar el plan óptimo de producción trimestral que maximice la ganancia en la producción de surtidos en la UEB 102, perteneciente a esta empresa.

 

Algunos elementos teórico-prácticos importantes

Una de las aplicaciones económicas más importantes de la programación lineal viene dada por su uso en la optimización de la producción, a través de modelos lineales, de forma tal que sean utilizadas las materias primas disponibles para obtener máximos beneficios o mínimos costos.

En caso de no aceptarse valores fraccionarios en la salida de los modelos lineales, es preferible usar la programación lineal en enteros (PLE), la cual es una rama de la programación matemática orientada a la resolución de problemas, donde se requiere que al menos una de las variables de decisión en la solución óptima debe tomar un valor entero no negativo.

Existen problemas de la práctica económica que requieren definir un tipo de variable continua denominada "variable auxiliar entera" (VAE); esta es discreta en su comportamiento pues asume valores enteros cero o uno. Se asocia a la ejecución o no de una actividad j representada en el modelo lineal por la variable de decisión Xj.

El uso de métodos cuantitativos y, específicamente, el uso de la programación lineal y en enteros constituyen unas de las técnicas de la programación matemática más empleadas, ya que permiten evaluar entre un conjunto de soluciones posibles, aquella que resulte óptima, y atienden a un determinado criterio económico para el problema en cuestión. En el caso de la empresa Talabartería THABA, dichas técnicas se aplicaron a la toma de decisiones del proceso productivo de la organización, con el objetivo de determinar el nivel máximo de ganancia; para ello se combinaron eficientemente los insumos que requieren los diferentes surtidos y se tuvieron en cuenta las limitaciones materiales correspondientes. Para el tratamiento automatizado de la información, se utilizó el paquete informático denominado "Sistema para el análisis cuantitativo de negocios sobre el ambiente Windows" (WinQSB) y para el análisis se tomó como referencia la UEB 102, perteneciente a la citada empresa, ubicada en el municipio Guanabacoa.

En los últimos años la UEB 102 se ha especializado, fundamentalmente, en la producción de los siguientes surtidos: hamacas, maletín comando modelo 23/11, maletín comando modelo 21/10 y la mochila modelo 462/09. La hamaca constituye el producto de mayor demanda para la UEB 102, es destinada a las FAR, la cual asume los costos de las materias primas obtenidas en el exterior. Por su parte, los maletines comando modelos 23/11 y 21/10 mantienen durante todo el año una alta demanda, excepto en algunos meses que no se reciben pedidos. La mochila modelo 462/09 es, de forma general, uno de los productos que históricamente más han aportado a los ingresos de dicha organización, al igual que los maletines 23/11 y 21/10, que mantienen durante todo el año una alta demanda y parte de su producción es asumida por la UEB 102.

 

Formulación matemática del modelo lineal para la UEB 102 (modelo 1)

Variables esenciales:

Como se puede apreciar, las restricciones están formadas por los requerimientos tecnológicos por tipo de producto y las cotas máximas trimestrales disponibles de cada recurso. Los datos fueron tomados de las normas de consumo y las fichas de costo correspondientes a cada artículo.

 

Resultados obtenidos para el modelo 1 con la utilización del paquete informático WinQSB

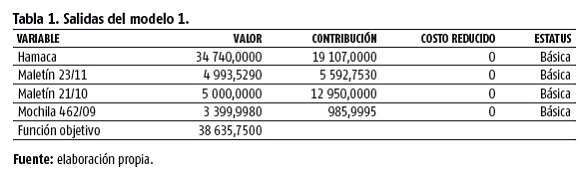
Una vez introducidos los datos en el paquete WinQSB y consideradas las variables esenciales de tipo continuo, se obtuvieron las salidas en el reporte combinado del modelo 1, para ver si es un caso en el cual los valores de todas las variables esenciales en la solución óptima son enteros. Los valores de las variables esenciales obtenidos con el modelo 1 se presentan en la tabla 1.

Como se puede observar, la solución es no degenerada, las cuatro variables esenciales resultaron básicas y proporcionaron 38 635,75 de ganancia en moneda total (MT). La variable que representa al producto hamaca es la que más aporta al valor de dicha ganancia con un 49 %, mientras que la que representa a la mochila es la que menos aporta con un 2 %, aproximadamente.

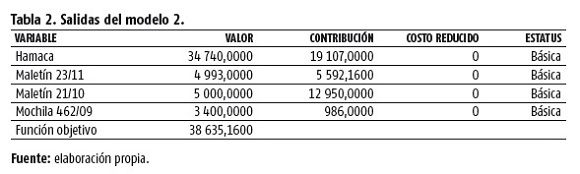
De un total de 36 recursos, 8 resultaron ser críticos (tienen holgura cero). El problema que se aborda requiere por su naturaleza el tratamiento matemático de un problema de programación lineal en enteros, ya que no tiene sentido para este caso obtener valores fraccionarios como los obtenidos para las variables segunda y cuarta. A continuación, se muestran en la tabla 2 los resultados obtenidos para las variables esenciales en el reporte combinado del modelo 2, que incluye la condición de entero para las variables esenciales en el modelo 1.

Con esta solución, donde todas las variables toman valores enteros, se puede ver como hay una ligera disminución en el valor de la ganancia. Se trata en este caso de un problema de maximización; el valor de la ganancia disminuyó en 0,59 MT y se mantiene la variable que representa al producto hamaca como la que más aporta al valor de la ganancia con un 49 %; y la que representa a la mochila, como la que menos aporta con un 3 %, aproximadamente. Al exigir valores enteros para las variables, el número de recursos críticos aumentó drásticamente de 8 a 18.

Los resultados obtenidos en principio para este problema resultan el óptimo técnico, es decir, las cantidades de los diferentes artículos que se deben elaborar para obtener la máxima ganancia con las limitaciones de recursos establecidas, es lo que matemáticamente se entiende por solución óptima para el problema si se supone un flujo productivo continuo de los diferentes productos. Sin embargo, en el caso de la UEB 102, no necesariamente se acomete la producción de los cuatro productos simultáneamente, pues en la mayoría de las ocasiones reciben solicitudes que incluyen solamente dos o tres de los productos, según la demanda de los clientes. Por esta razón, en realidad el óptimo técnico para la producción puede no coincidir con el óptimo económico en nuestro caso.

Como uno de los principales objetivos de la modelación matemática es acercarse de la mejor manera posible a la realidad; con este fin se puede recurrir al uso de recursos de la programación en enteros que potencian la programación lineal mediante las denominadas "condiciones lógicas"; para ello nos debemos basar en el uso de variables auxiliares enteras (VAE) asociadas a cada una de las variables esenciales definidas en el modelo.

 

Modelos y resultados obtenidos utilizando condiciones lógicas

Las cuatro condiciones lógicas utilizadas en el análisis se explican a continuación.

 

Condición lógica n.o 1

No elegir más de k alternativas de un conjunto de m posibles. Se logra incluyendo la restricción en el sistema de restricciones lineales. Para este problema con y después de largo tiempo utilizando el método Branch and Bound, el paquete WinQSB no encontró solución óptima.

 

Condición lógica n.o 2

No elegir la opción k a menos que se elija primero la opción l. Se logra incluyendo la restricción en el sistema de restricciones lineales. En este caso, se impuso que no se hicieran los productos maletín modelo 23/11, maletín modelo 21/10 y la mochila modelo 462/09, a menos que se hiciera primero el producto hamaca, ya que este constituye el producto que mantiene una demanda constante a lo largo del trimestre, es decir, que no hicieran por elección las unidades de maletín 23/11 si no se hacen primero unidades de hamacas (modelo 4); igual con las unidades de maletín 21/10 si no se hacen primero unidades de hamacas (modelo 5) y las unidades de mochila 462/09 si no se hacen primero unidades de hamacas (modelo 6).

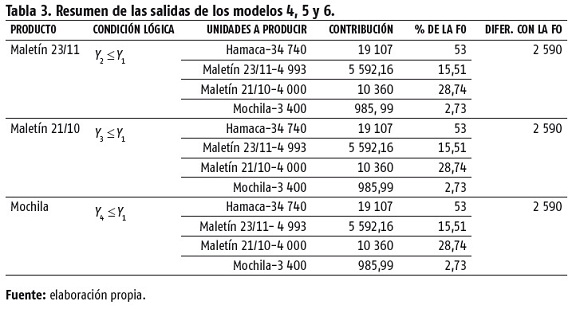
A modo de resumen, se muestra en la tabla 3 el resultado obtenido dirigido a las variables esenciales para los modelos 4, 5 y 6.

El resultado obtenido muestra cómo en los tres casos se pueden realizar todas las actividades al respetar la condición lógica impuesta, ya que la VAE Y1 toma siempre valor 1,00 al igual que las VAE Y2, Y3 y Y4. El valor de la ganancia (función objetivo) en los tres casos fue de 36 045,16 MT y, por consiguiente, su diferencia es de 2 590 MT con el mayor valor de la ganancia, que se obtiene donde las variables toman valores enteros que corresponde al modelo 2. De esta forma, de las variables esenciales que se están condicionando respecto a la variable que representa a la hamaca, la que más contribuye a la función objetivo es la que tiene asociada la VAE Y3 (maletín 21/10) con un valor de 10 360 MT de ganancia, y la que menos aporta es la que tiene asociada la VAE Y4 (mochila 462/09) con un valor de 985,99 MT, para un 28,74 % y 2,73 %, respectivamente.

 

Condición lógica n.o 3

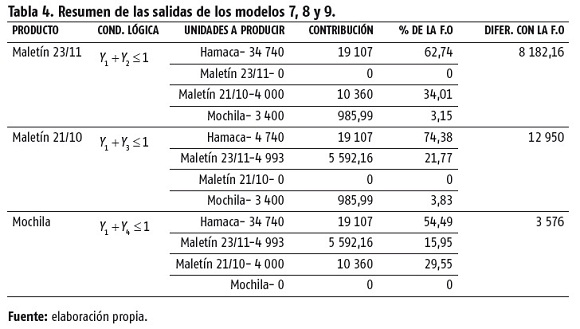
Actividades que se excluyen mutuamente, no estrictamente. Se logra incluyendo la restricción en el sistema de restricciones lineales. Esta condición lógica impone que si se realiza la actividad k no se realice la actividad l o viceversa, o que no se realice ninguna de ellas. El modelo 7 se obtuvo al incluir en el modelo 3 la condición ; el modelo 8, al incluir en el modelo 3 la condición ; y el modelo 9, al incluir en el modelo 3 la condición . A modo de resumen, el resultado obtenido para las variables esenciales correspondientes a los modelos 7, 8 y 9 se muestra en la tabla 4.

Como se puede apreciar en los tres modelos, la solución es cero para la variable que se está condicionando respecto a la que representa a la hamaca, lo que significa que siempre se debe producir la hamaca. Las diferencias entre estas radican en el valor de la ganancia (de la función objetivo) respecto a la solución, donde las variables esenciales toman valores enteros. La mejor combinación es producir los productos hamaca, maletín 23/11 y maletín 21/10, porque es la solución donde la ganancia que se obtiene se acerca al mayor valor obtenido para la ganancia en los modelos utilizados.

 

Condición lógica n.o 4

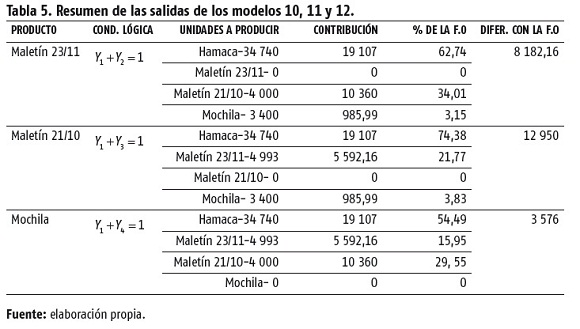
Actividades que se excluyen mutuamente, estrictamente. Se logra incluyendo la restricción en el sistema de restricciones lineales. Esta condición lógica impone que si se realiza la actividad k no se realice la actividad l o viceversa, pero se debe garantizar la ejecución de una de las dos. El modelo 10 se obtuvo al incluir en el modelo 3 la condición ; el modelo 11, al incluir en el modelo 3 la condición ; y el modelo 12, al incluir en el modelo 3 la condición. A modo de resumen, el resultado obtenido para las variables esenciales correspondientes a los modelos 10, 11 y 12 se puede observar en la tabla 5.

En este caso, los resultados obtenidos son similares a los alcanzados donde se aplicó la condición lógica n.o 3. Las VAE Y2, Y3 y Y4 arrojaron valor de solución igual a cero en cada uno de los modelos 10, 11 y 12; esto significa que hay que realizar la producción de hamacas en todas las combinaciones.

Al igual que en la condición lógica anterior, la alternativa que menos diferencia presenta respecto a la ganancia obtenida en el modelo 1 es la producción de los productos hamaca, maletín 23/11 y maletín 21/10.

 

Resumen del análisis de las salidas obtenidas en los 12 modelos estudiados

La combinación que puede proporcionar mayor ganancia trimestralmente, si se elaboran todos los productos en la UEB 102, es la producción de 34 740 hamacas, 4 993 maletines 23/11, 5 000 maletines 21/10 y 3 400 mochilas 462/09 con 38 635,16 MT de ganancia y 18 recursos críticos.

En el caso de que no se elaboren todos los productos, la combinación que proporcionará mayor ganancia en el trimestre es la producción de 34 740 hamacas, 4 999 maletines 23/11 y 5 000 maletines 21/10 con una ganancia de 35 059,16 MT y 3 recursos críticos (no producir mochilas 462/09).

Los resultados anteriores son válidos solamente en este estudio para las cotas de recursos fijados. Si cambian, es necesario volver a correr los 12 modelos empleados, pero ajustados a las nuevas condiciones.

 

CONCLUSIONES

La modelación realizada determinó el plan óptimo de producción trimestral que maximiza la ganancia si se producen los cuatro artículos o un subconjunto de ellos, y refleja lo que ocurre en la práctica económica, ya que en la UEB 102 el producto de mayor volumen de producción es la hamaca pues está presente en todas las combinaciones citadas que maximizan la ganancia.

Puede ser conveniente estudiar el comportamiento de la demanda histórica por trimestres para fijar los planes de producción; para ello se debe correr los modelos de programación en enteros mixtos que establezcan cantidades de productos "acotados en un intervalo" según la demanda, lo cual resultará más racional económicamente.

 

Recomendaciones

Se recomienda tomar en cuenta los resultados obtenidos en el trabajo para la planificación de los planes de producción trimestrales en la UEB 102, conjuntamente con el comportamiento de la demanda y otros factores, y refinar el estudio realizado si resulta de interés diferenciar las cantidades de productos que deben elaborarse con destino a mercados en diferentes tipos de moneda, tanto para el mercado en frontera como para exterior.

 

 

REFERENCIAS BIBLIOGRAFICAS

 

Castillo, E. Formulación y resolución de modelos de Programación Matemática en ingeniería y ciencia, New York, Academic Press, (2002).

Nocedal, A. J. Numerical Optimization, Springer, New York, (1999).

Rao, S. S. Engineering Optimization. Theory and Practice, New York, Wiley, (1996).

Hiriart-Urruty, J. B. Convex Analysis and Minimization, Berlin, Springer-Verlag, (1996).

VV. AA. Programación matemática I, La Habana, Editorial Félix Varela, (2001).

 

 

 

RECIBIDO: 13/11/2013

ACEPTADO: 17/3/2014

 

 

 

Eduardo Martínez Puig. Facultad de Economía, Universidad de La Habana, Cuba. Correo electrónico: [e-mail]