Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Cultivos Tropicales
versión impresa ISSN 0258-5936
cultrop vol.32 no.3 La Habana jul.-set. 2011
Inconsistencia del Coeficiente de Variación para expresar la variabilidad de un experimento en un modelo de Análisis de Varianza
Inconsistency of the coefficient of variation for expressing the variability of an experiment in a model of analysis of variance
Edison Ramiro Vásquez1 y Alberto Caballero Núñez2
1 Universidad Nacional de Loja (UNL) , Ecuador
2 Instituto Nacional de Ciencias Agrícolas (INCA), Cuba
RESUMEN
A partir de una variable normalmente distribuida con media cero y varianza uno, se generó una sucesión de p tratamientos con varianza constante igual a uno y cuyas medias se incrementaban en k unidades, válidas para conformar sendos experimentos; uno con los tprimeros tratamientos de la sucesióny otro con los p-trestantes; se comprobó que a pesar que ambos experimentos mantenían iguales sus estimaciones de varianza de error experimental, sus Coeficientes Variación son diferentes. Como ilustración práctica se analizarontres experimentos mediante un Análisis de Varianza, los cuales tenían la misma varianza y diferente estructura de medias de sus cuatro tratamientos. Los tres experimentos presentarondiferentes coeficientes de variación a pesar que sus estimaciones de varianza del error experimental eran las mismas, lo cual pone en evidencia que este estadígrafo no refleja exactamente la variabilidad existente en un experimento cuando es analizado a través de un Análisis de Varianza. Tampoco el coeficiente de variación se asoció con el nivel de significacióno capacidad de la prueba de F para detectar diferencias significativas entre medias de tratamientos, ni con el rango entre los valores de las medias de tratamientos.
Palabras claves: Coeficiente de Variación, varianza del error experimental, Análisis de Varianza
ABSTRACT
From a variable distributed normally with mean zero and variance one, arose a succession of p treatments with constant variance equal to one and whose mean increased k units, valid to form two separate experiments; one with the t first treatments of the succession and the other with the remaining p; It was found that despite the fact that both experiments maintained equals its estimate of experimental error variance, its variation coefficients are different. As a practical illustration were analyzed three experiments through an analysis of variance, which had the same variance and different structure of half of its four treatments. The three experiments presented different coefficients of variation in spite that their estimates of variance of the experimental error were the same, which shows that this statistician does not accurately reflect the variability existing in an experiment when it is parsed through an analysis of variance. Also the coefficient of variation was associated with the level of significance or capability of the F test to detect significant differences between treatments, or the range between the values of the averages of treatments.
Key words: coefficient of variation, variation of the experimental error, analysis of variance
INTRODUCCIÓN
El coeficiente de variación de Pearson, ha resultado ser una medida dedispersión de amplia utilización,cuando se pretende comparar la dispersión entre varias poblaciones, de una o diferentes variables medidas en la misma o diferentes escalas. Este estadígrafo es definido como la relación por cociente que se establece entre la desviación estándar y la media aritméticade la variable; dicho de otro modo, desviación estándar expresada como porcentaje de la media aritmética, [1][2] y [3]; esto lo hace un coeficiente adimensional, invariante por la escala de medición de la variable analizada. Todo lo anterior justifica la preferencia de utilizarlocuando el propósito en la investigación sea la comparación de poblaciones desde el punto de vista de su variabilidad, [4],[5] y[6].
Sin embargo, el hecho de estar conformado por una razón entre dos estadígrafos que reflejan diferentes características en la población, cualquier interpretación acerca de este coeficiente debe ir unida a un análisis de las peculiaridades del problema tratado y el comportamiento de cada uno de estos dos estadígrafos. En este contexto, es preciso tener en cuenta que la desviación estándar es invariante ante la relación suma, no así la media; de otro modo, si a cada valor de una la muestrase le suma una constante k, la muestra resultante conserva su desviación estándar; y su media se afecta en kunidades; por tanto, su coeficiente de variación será diferente al de la muestra inicial.
Teniendo en cuenta lo anterior, se puede esperar que en los modelos de Análisis de Varianza, en los que se analizan sendos experimentos con similar estimación de varianza del error experimental, pero con diferente composición de medias de tratamientos, quepueden aportar medias generales distintas, los coeficientes de variación pueden resultardiferentes.
En este contexto, el objetivo del presente trabajo está dirigido a ilustrar la inconsistencia que tieneel Coeficiente de Variación para explicar la variabilidad de los experimentos analizados según un modelo de Análisis de Varianza.
MATERIALES Y MÉTODOS
Para cumplir con el objetivo propuestose hace uso de la propiedad que plantea: dada una variable aleatoria X normalmente distribuida con media y varianza , si a cada uno de los valores que componen la población se le suma una constante k>0, se origina una nueva variable aleatoria que mantiene la varianza y la media se incrementa en la constante k.
Para el desarrollo teórico:
Se generó una sucesión de p poblaciones de variables aleatorias X(1), X(2),…, X(p), de modo que X(i) = X(i-1) + k.
![]()
Las poblacionesX(1), X(2), …, X(t), …, X(p-t),…, X(p),se utilizaron para conformar los tratamientos de dos experimentos; Experimento 1 y Experimento 2, siguiendo la siguiente estructura:
Experimento 1: Sus tratamientos se corresponden con last primeras poblaciones de la sucesión:

Experimento 2: Sus tratamientos se corresponden con last últimas poblaciones de la sucesión:
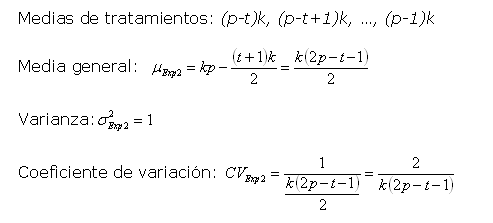
Se generó una población (A) normalmente distribuida con media 10 y varianza 25; a partir de esta, se generaron nuevepoblaciones (B, C,…, J), cuyas medias se incrementaron respectivamente en un valor de k= 2, 4,…,18 que conservan la misma varianza (Tabla I).
Se conformaron tres experimentos: (Tabla II)
• Experimento 1: Tratamientos A, B, C, D ( 4 primeras poblaciones)
• Experimento 2: Tratamientos G, H, I, J ( 4 últimas poblaciones)
• Experimento 3: Tratamientos A, E, F, J (la primera, las dos del centro y la última población)
RESULTADOS Y DISCUSIÓN
Desarrollo teórico:
Para comprobar la igualdad o no entrelos coeficientes de variación se calculó el cociente entre ellos:
En efecto, siendo p >t, hace que este estadígrafo, definido como el cociente entre la desviación estándar de la muestra y su media,ofrece una estimación de la proporción de variabilidad de la muestra expresada por unidades de media y no la variabilidad en sí de dicha muestra [1] y [2]. De aquí que en variables previamente estandarizadas,este estadígrafo no puede ser definido [3]; y en variables cuya media se aproxime a cero, su valor tiende a elevarse.
Los dos experimentos poseenigual varianza del error experimental,lo cual significa que la variabilidad entre unidades experimentales dentro de los respectivos tratamientos en cada experimento es la misma; no obstante, como susmedias generales son diferentes, el Experimento 1 posee mayor coeficiente de variación que el Experimento 2.
Lo anterior está asociado con la propia definición de este estadígrafo, que además de ser una función de la varianza, lo es también de la media, característica que lo hace variable ante los cambios de origen de escala, como loseñalan muchos autores, entre otros [1] y [2].
Ilustración práctica
En laTabla III se exponen los resultados del Análisis de Varianza de un factor con cuatro tratamientos y 10 repeticiones.
Como se aprecia, en tres experimentos los Cuadrados Medios de Error; estimación de la varianza del error experimental o la varianza entre unidades experimentales dentro de cada tratamiento, son iguales; mientras que sus respectivas medias generales son diferentes, ellos hace que las estimaciones de Coeficientes de Variación también lo sean, mayor en el experimento con menor media general. Esto se debe a que la media general está notablemente influenciada por la estructura de las t medias de tratamientos que conformaexperimento, (Tabla II).
Cabe resaltar que en experimento analizado a través de un modelo de Análisis de Varianza el Coeficiente de Variación, expresa la proporción de la variabilidad del error experimental por unidades de media general y no el de la varianza del error experimental o la variabilidad absoluta del error del experimento. Lo cual evidencia que este estadígrafo es incapaz de reflejar en si la variabilidad de dicho experimento, de aquí el cuidado que se debe tener en su interpretación ante estas situaciones.
Dado que los tres experimentos presentan igualdad en las estimaciones de varianza del error experimental, existe una clara asociación entre el nivel de significación con el cual se declaran diferencias entre medias de tratamientos a través del Análisis de Varianza y el rango entre dichas medias, a favor del experimento que posee rango mayor.
No se observa asociación entre el Coeficiente de Variación ni la varianza del error experimental con los rasgos descritos anteriormente; por tanto, estos estadígrafos no ofrecenuna idea exacta de la capacidad del ANOVA para detectar una diferencia significativa entre medias de tratamientos; tampoco el rango de variación entre las medias de tratamientos constituye un indicador que refleje la variabilidad del error experimental.
Todo lo anterior pone en evidencia la poca sostenibilidadde establecer rangos en los que se debe ubicar este estadígrafo en un experimento para decidir acerca la calidad del experimento en su ejecución.
Resulta imprescindiblehacer ciertas precisiones relacionado con los resultados de este trabajo y el uso que se ha hecho del Coeficiente de Variación.
Es indudable que la elección de este estadígrafo es obligada cuando se pretende comparar la variabilidad de dos o más poblaciones medida en igual o diferente escala; ningún otro estadígrafo de variabilidad es capaz de ofrecer información tan valiosa en tales situaciones.
Enumerarlos trabajos en las que se hace uso acertado de este estadígrafo y su correcta interpretación, puede resultar un imposible. En tal sentido, solo se expondrán algunas situaciones en el que el uso del Coeficiente de Variación ha logrado extraer valiosa información para la población en disímiles campos de investigación: la Oficina Nacional de Estadística de Cuba ha evaluado la precisión de los resultados en cuanto a la calidad y la cobertura del Censo de Población y Vivienda del 2002 en Cuba[4] a través de unuso eficiente de este estadígrafo; del mismo modo la Departamento Administrativo Nacional de Estadística, DANE, de Colombia [5]hace uso de este estadígrafo para medir el error muestral durante el Censo del Población del 2005. Otro ejemplo no menos importante se presenta [6] con la utilización de este estadígrafo para evaluar el nivel de uniformidad en la distribución de los abonos.
De todo lo anterior se recomienda que en modelos de Análisis de Varianza, no se emplee el Coeficiente de Variación como indicador de la variabilidad experimental, ni establecer rango de sus magnitudes para asociarla con la calidad de conducción del experimento.
REFERENCIAS
1. Barón López, F.J.; Bioestadística: Métodos y AplicacionesU.D. Bioestadística. Facultad de Medicina. Universidad de Málaga.ISBN: 847496-653-1
2.Cabrera G. F.. Propiedades del Coeficiente de Variación www.monografias.com
3. Ruiz y Sánchez (2006) Apuntes de Estadística. Edición electrónica. [Consultado: 01-2011]. Disponible en: www.eumed.net/libros/2006/rmss/
4. Oficina Nacional de Estadística, Cuba. Censo de Población y Vivienda 2002. Aplicaciones del muestreo en el Censo de Población y Viviendas.[Consultado: 01-2011]. Disponible en http://www.cubagob.cu/otras_info/censo/c_vi.htm
5. Estimación e interpretación del Coeficiente de Variación de la encuesta cocensal. Censo General 2005 – CGRAL. Junio 2008.[Consultado: 01-2011]. Disponible en:http://www.dane.gov.co/files/investigaciones/boletines/censo/est_interp_coefvariacion.pdf
6. Gil E..Elementos clave en la uniformidad de distribución de abonos. Escuela Superior de Agricultura de Barcelona.[Consultado: 01-2011]. Disponible en http://e-md.upc.edu/diposit/material/22459/22459.pdf
Recibido 18/03/2011, aceptado 08/06/2011.













