ARTÍCULO ORIGINAL

 

Modelo matemático para estimar el valor genético de progenitores y cruces en caña de azúcar

 

Mathematical model to estimate the genetic value of progenitors and crossings in sugar cane

 

 

Dr.C. Reynaldo Rodríguez-Gross,^I Dra.C. Yaquelin Puchades-Isaguirre,^I Wilfre Aiche-Maceo,^I Dra.C. María T. Cornide-Hernández^II

^I Grupo de Genética y Protección de Plantas. Estación Territorial de Investigaciones de la Caña de Azúcar Oriente Sur, Cuba. (22) 502254.

^II Grupo de Genética y Protección de Plantas. Instituto de Investigaciones de la Caña de Azúcar, Cuba.

 

 

---

RESUMEN

La selección de progenitores es una de las etapas más importantes en cualquier programa de mejora para obtener ganancia genética. El objetivo del presente trabajo fue proponer un modelo matemático para estimar, a partir de la información de selección, el valor genético de progenitores y cruces con el procesamiento de diversas variables en sus progenies en caña de azúcar en Cuba. Para esto se utilizó la información de las primeras tres etapas de selección (posturas, propagación clonal 1 y 2) del programa de mejora desarrollado en la región sur-oriental de Cuba, desde el año 2000 al 2007. Asimismo, se recurrió al sistema informático SASEL, utilizado en el mejoramiento genético de la caña de azúcar, para programarle el modelo matemático propuesto. El modelo permitió estimar, de forma multivariada, el valor genético de los progenitores y cruces utilizados en el programa de mejoramiento genético de la caña de azúcar en Cuba. Se pudo establecer, a partir de la predicción de este valor, los progenitores y cruces más destacados en el período analizado, lo que constituye una herramienta útil para contribuir al perfeccionamiento del programa de mejora.

Palabras clave: genética, informática, selección.

---

ABSTRACT

Parental selection is one of the most crucial steps to improve genetic gain in any breeding program. The objective of the present work was to propose a mathematical model to estimate, from the selection information, the genetic value of parents and crosses with the processing of various variables in their progenies in sugarcane in Cuba. For this, information was used from the first three stages of selection (postures, clonal propagation 1 and 2) of the improvement program developed in the south-eastern region of Cuba, from 2000 to 2007. Likewise, the computer system was used SASEL, used in the genetic improvement of sugarcane, to program the proposed mathematical model. The model allowed estimating, in a multivariate way, the genetic value of the parents and crosses used in the genetic improvement program of sugarcane in Cuba. It was possible to establish, from the prediction of this value, the most outstanding parents and crosses in the analyzed period, which constitutes a useful tool to contribute to the improvement of the improvement program.

Key words: genetic, software, selection.

---

 

 

INTRODUCCIÓN

La selección de progenitores y la predicción de su valor es una de las accionesmásimportantes en cualquier programa de selección (1). Por lo tanto, el incremento de la selección y la ganancia genética es una medida importante del éxito de los programas de mejoramiento (2).

En el proceso de selección en caña de azúcar, particularmente en las primeras etapas, se evalúan varios caracteres que componen el rendimiento agrícola e industrial, así como la incidencia de enfermedades. Una metodología de selección simultánea es necesaria para estas primeras etapas, lo cual constituye la base de selección sobre un índice a partir de múltiples caracteresmásquela selección intensiva sobre un carácter en particular (3).

En la actualidad, es ampliamente aceptado que los modelos matemáticos pueden proveer herramientas valiosas para el estudio del comportamiento de las plantas, a la vez que contribuyen a ahorrar experimentos de campo, recursos y tiempo (4–6). Los análisis estadísticos de correlación y regresión lineal son frecuentemente usados para la evaluación de modelos (7).

El Instituto de Investigaciones de la Caña de Azúcar de Cuba desarrolla un programa de mejoramiento genético para dar respuesta a la obtención de nuevos cultivares. Esto significa que anualmente maneja una población grande de clones en diferentes etapas y años de selección. Para tal fin se dispone de un programa informático (SASEL) que permite capturar, almacenar y procesar la información obtenida en el proceso de selección (8). Sin embargo, este programa no posee un modelo que permita estimar el valor genético de progenitores y cruces a partir de la información de selección.

El objetivo del presente trabajo es proponer un modelo matemático para estimar, a partir de la información de selección, el valor genético de progenitores y cruces con el procesamiento de diversas variables en sus progenies en caña de azúcar.

 

MATERIALES Y MÉTODOS

Información utilizada en el modelo

Se utilizaron los datos de selección provenientes de las tres primeras etapas del programa de mejora genética de la caña de azúcar que se desarrolla en la región sur-oriental de Cuba. El período de selección genética comprendió los años desde el 2000 hasta el 2007 (Tabla I).

Los ensayos fueron establecidos en el área experimental de la localidad de América Libre del municipio Contramaestre en la provincia Santiago de Cuba (-76,2 ° longitud y 20,3° latitud) sobre un suelo Pardo sialítico. La conducción de los estudios se realizó según las normas metodológicas del programa de mejora genética de la caña de azúcar en Cuba (9).

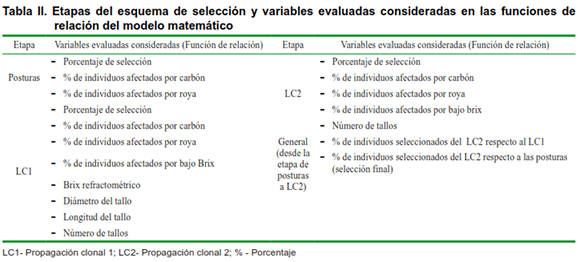
Para la construcción del modelo se tuvieron en cuenta un total de 18 variables que a su vez constituyen los criterios de selección en cada una de las etapas consideradas (Tabla II). Estas informaciones obtenidas en el campo, fueron capturadas y validadas por el software SASEL. Las tres etapas de selección genética y los años de estudio comprendieron una base de datos compuesta por la información de las progenies de 242 y 110 progenitores femeninos y masculinos respectivamente, así como, 640 cruces biparentales, lo que permitió establecer el modelo matemático.

Modelo matemático para estimar el valor genético de progenitores y cruces

Se utilizó un modelo lineal para cuantificar la interacción existente entre el genotipo (progenitor) o el cruce y el ambiente (interacción genotipo-ambiente) a través de la siguiente función F, que depende del progenitor o cruce ´x´ y el ambiente ´y´.

donde:

Ci(x,y), 0 <= Ci(x,y) <= 1 para (i= 1,2,…,N) son las funciones de relación entre el progenitor o cruce “x” con el ambiente “y”.

∝_i, 0 <= ∝_i <= 1 para (i= 1,2,…,N) son los coeficientes de ponderación de las funciones de relación.

i, es la función de relación específica que se incluyen en el modelo matemático

N, es la cantidad total de funciones de relación que se incluyen en el modelo matemático.

La cantidad de funciones de relación (variables evaluadas a las progenies de los progenitores o cruces) a emplear en el modelo matemático está en función de los intereses del mejorador y de la etapa o etapas que se decida utilizar. El modelo matemático es flexible y permite orientarse en dependencia de los objetivos de mejoramiento que se persigan. Igualmente, los coeficientes de ponderación se pueden modificar en función de los objetivos de selección y la importancia relativa de las variables a considerar.

Para convertir los valores evaluados de las variables utilizadas en la función C_i(x,y) con rango entre cero y uno (0 <= Ci(x,y) <= 1, para (i= 1,2,…,N)) se utilizó el siguiente procedimiento:

X_iY – Valor de la variable evaluada del progenitor o cruce i en el ambiente Y

Max X_i,Y – Máximo valor encontrado de la variable utilizada del progenitor o cruce i en el ambiente Y

 

RESULTADOS Y DISCUSIÓN

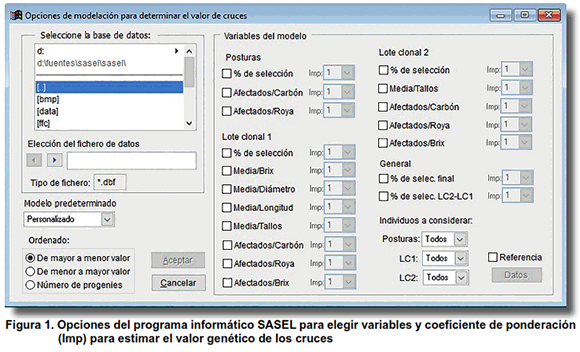
El modelo matemático propuesto ofrece la posibilidad de utilizar en su conformación hasta 18 variables que constituyen criterios de selección en las tres etapas de selección consideradas (Figura 1). También permite modificar el coeficiente de ponderación (denominado Imp.) de cada una de estas variables, a partir de la importancia relativa de las variables. Este coeficiente oscila entre cero y uno, y puede considerarse, en algunas variables, como una interpretación de la heredabilidad. En este caso se encuentran las variables relacionadas con el brix, componentes del rendimiento agrícola y la resistencia a enfermedades.

Al definirse por el mejorador las variables a considerar y el peso relativo de las mismas (coeficiente de ponderación) el modelo matemático estima el valor genético de los cruces contenidos en la base de datos de selección o de los progenitores según se escoja. Este valor se estima a partir de la evaluación realizada a sus progenies y le permite al mejorador seleccionar los cruces o progenitores con mejor respuesta de acuerdo a los objetivos que se persigan.

Asimismo, se puede restringir la cantidad de cruces a considerar por el modelo, al discriminar los cruces que posean bajo número de progenies evaluadas (opción ´Individuos a considerar´). Esta posibilidad permite aumentar la precisión del modelo matemático debido a que estima el valor genético de progenitores y cruces con mayor número de progenies evaluadas.

Otras opciones del menú del modelo permiten insertar, previo al cálculo del valor genético de los cruces, los valores ideales o de “referencia” de las variables consideradas. Es decir, a partir de estos valores introducidos, el modelo determina el valor ideal o esperado del cruce y posibilita establecer un límite para considerar los cruces como destacados o a descartar.

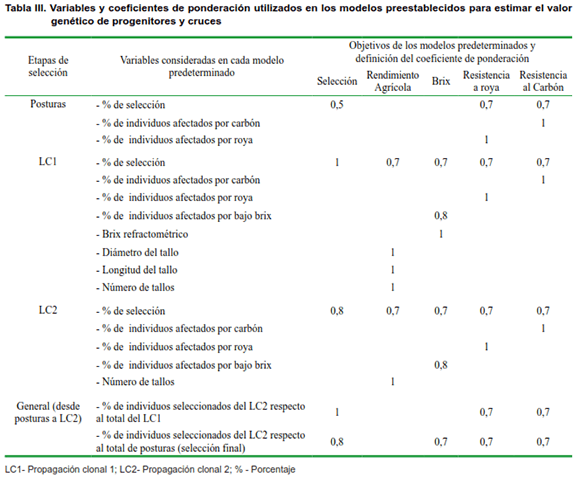
A partir de los objetivos de selección en el cultivo de la caña de azúcar (9) y para facilitar el trabajo del mejorador se establecieron cinco modelos predeterminados que estiman el valor genético de progenitores y cruces (Tabla III). Como se puede apreciar para cada modelo se escogieron las variables que definen los objetivos de mejora en la caña de azúcar. Esto no significa que el mejorador pueda incluir o excluir otras variables en el modelo según los objetivos que se desee.

Los modelos predeterminados están encaminados a obtener un estimado del valor de progenitores y cruces por diferentes objetivos de mejora como son: aporte de selección, contenido azucarero (brix), resistencia a enfermedades como roya y carbón de la caña de azúcar, así como rendimiento agrícola. En todos los casos, la variable que sistemáticamente se consideró en los cinco modelos fue el porcentaje de selección en las etapas de propagación clonal 1 y 2. Estas variables son importantes debido a que resumen las cualidades del individuo en su conjunto.

Al escoger un modelo orientado a obtener un estimado del valor genético de cruces y progenitores por el rendimiento agrícola, se habilitan las variables que componen el rendimiento agrícola como diámetro, longitud y número de tallos con un máximo coeficiente de ponderación. Al mismo tiempo, se incluyeron las variables de selección (porcentaje de selección en etapa de propagación clonal 1 y 2) con coeficientes de ponderación de 0,7.

Así, cuando el objetivo del modelo no fue estimar el valor genético de progenitores y cruce por su aporte a selección, los coeficientes de ponderación de las variables de porcentaje de selección, se redujeron para maximizar los coeficientes de las otras variables del modelo. Estos valores de ponderación se determinaron a partir de la presión de selección que se establece por etapas de selección (9) y las numerosas simulaciones que se realizaron con las series estudiadas.

Para el caso de estimar el valor genético de los progenitores femeninos y masculinos las opciones del menú del modelo matemático son las mismas, con la diferencia que aparece una opción de escoger si se va a trabajar con los progenitores femeninos o masculinos.

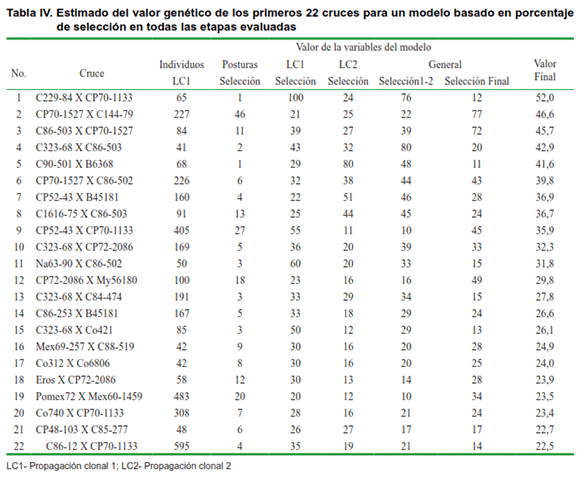
Al ejecutar el modelo matemático predeterminado (aporte de selección) se pudo estimar el valor genético de los cruces (Tabla IV). Los cinco primeros cruces con mayor valor alcanzado fueron: C229-84 x CP70-11333, CP70-1527 x C144-79, C86-503 x CP70-1527, C323-68 x C86-506 y C90-501 x B6368. Estos cruces lograron un valor superior al 40 %, lo que pudiera indicar una alta habilidad combinatoria específica.

De igual forma, el resto de los cruces, también alcanzaron un alto valor genético respecto a los 640 cruces manejados en la base de datos de estudio. De modo particular, se pueden señalar cruces que alcanzaron un alto valor con alto número de progenies evaluadas. Estos cruces fueron: C86-253 x B45181 (26,6 %), Pomex72 x Mex60-1259 (23,5 %), Co470 x CP70-1133 (23,4 %), Co740 x CP70-1133 (23,5 %) y C86-12 x CP70-1133 (22,5 %). Este último cruce son los progenitores del cultivar C00-575 obtenida y recomendada para las condiciones ambientales de la provincia Santiago de Cuba (10).

Los valores más bajo de las variables relacionadas con el porcentaje de selección, corresponden a la etapa de posturas y selección final. Esto puede deberse a varios factores como son: alta población de individuos en la etapa inicial respecto a los que finalmente se seleccionan en propagación clonal 2, efectos de competencia en la fase de posturas, así como criterios y presión de selección en las tres etapas de mejoramiento genético.

Al Igual que para los cruces, el modelo estima el valor genético de progenitores femeninos y masculinos (Tabla V y VI). Los progenitores femeninos con mayor aporte de selección y valor superior al 40 % fueron: B80-250, CP70-1133, Na63-90, C1616-75, CP45-105, C86-407 y C90-501. Estos progenitores se destacaron fundamentalmente por su aporte de selección en las etapas de propagación clonal 1 y 2, así como porcentaje de selección en la propagación clonal 1 respecto a la 2. Estos resultados evidencian una alta habilidad combinatoria general de estos progenitores.

Dentro de este grupo de progenitores femeninos, es de destacar a la C90-501 por su alto estimado de valor genético y a la vez elevadonúmero deprogenies evaluadas (1045).

También, con un alto número de progenies evaluadas y elevadoestimado del valor genético respecto al total de progenitores estudiados se encuentran: C323-68 (36,7 %), C86-456 (35,8 %), CP52-43 (34,2 %), C229-84 (30,4 %) , C1051-73 (29,6 %), CP70-1527 (29 %) y C88-553 (27,9 %).

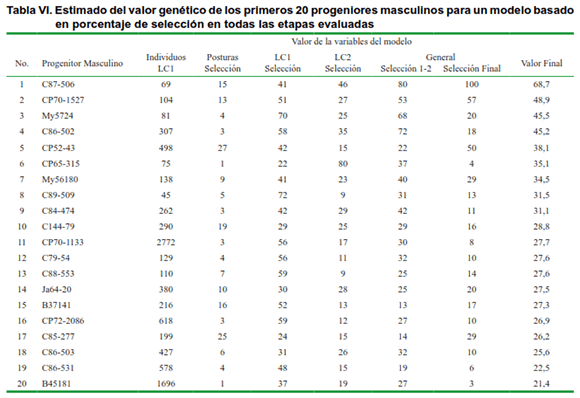
Respecto a los progenitores masculinos, según el estimado del valor genético del modelo, los primeros cuatro genotipos con porcentaje superior al 40 %, se destacan los siguientes: C87-506, CP70-1527, My5724 y C86-502. Igualmente se destacan otros genotipos con alto número de progenies evaluadas, lo que le confiere significación a los resultados obtenidos por el modelo. En este sentido se destacan los siguientes progenitores: CP52-43 (38,1 %), CP70-1133 (27,7 %), CP72-2086 (26,9 %), C86-503 (25,6 %), C86-531(22,5 %) y B45181 (21,4 %). Al igual que para los progenitores femeninos, los altos estimados del valor genético de estos progenitores masculinos evidencian una alta habilidad combinatoria general.

El uso de los modelos BLUP (Mejor Predictor Lineal no Sesgado) es el procedimiento más habitual para estimar los componentes de varianza y el valor de cruzamientos (11,12). Sin embargo, requieren, para su mejor estimación, información sobre el árbol genealógico de los progenitores (1,13).

El modelo propuesto en este estudio ofrece un estimado del valor genético de un progenitor o cruce, a partir de la respuesta de sus progenies en el programa de selección genética de la caña de azúcar en Cuba. Así, permite valorar a los mejoradores, a través de las tres primeras etapas de selección, la utilización o no de cruces y progenitores según los objetivos de mejora, a la vez que posibilita perfeccionar el programa de cruzamiento establecido con el fin de obtener un nuevo cultivar con características superiores a los testigos.

Otros autores utilizan la evaluación del mejoramiento de plantas y clasificación de genotipos por medio de rangos fenotípicos con el uso de árbol de desición y el método de regresión logística en etapas tempranas de selección (14,15). No obstante, el uso de uno u otro método o su combinación es impresindible para evaluar la ganancia genética y eficiencia en los programas de mejoramiento genético.

 

CONCLUSIONES

El modelo matemático propuesto permitió estimar, de forma multivariada, el valor genético de progenitores y cruces utilizados en el programa de mejoramiento genético de la caña de azúcar en Cuba. De esta forma, permite valorar, a través de las tres primeras etapas de selección, la utilización o no de cruces y progenitores según los objetivos de mejora, a la vez que posibilita perfeccionar el programa de cruzamiento establecido con el fin de obtener un nuevo cultivar con características superiores a los testigos.

 

BIBLIOGRAFÍA

1. Atkin FC, Dieters MJ, Stringer JK. Impact of depth of pedigree and inclusion of historical data on the estimation of additive variance and breeding values in a sugarcane breeding program. Theoretical and Applied Genetics. 2009;119(3):555–65. doi:10.1007/s00122-009-1065-7

2. Zhou MM, Gwata ET. Location effects and their implications in breeding for sugarcane yield and quality in the midlands region in South Africa. Crop Science. 2015;55(6):2628–38. doi:10.2135/cropsci2015.02.0101

3. Tahir M, Hussain Khalil I, McCord PH, Glaz B, Todd J. Phenotypic Selection of Sugarcane (Saccharum spp.) Genotypes using best linear unbiased predictors. Journal of American Society of Sugarcane Technologists. 34:44–56.

4. Herndl M, Shan C-G, Pu W, Graeff S, Claupein W. A model based ideotyping approach for wheat under different environmental conditions in North China plain. Agricultural Sciences in China. 2007;6(12):1426–36. doi:10.1016/S1671-2927(08)60004-8

5. Letort V, Cournède P-H, Mathieu A, De Reffye P, Constant T. Parametric identification of a functional–structural tree growth model and application to beech trees (Fagus sylvatica). Functional plant biology. 2008;35(10):951–63.

6. Rodríguez Gross R, Puchades Izaguirre Y, Abiche Maceo W, Rill Martínez S, Suarez HJ, Salmón Cuspineda Y, et al. Estudio del rendimiento y modelación del período de madurez en nuevos cultivares de caña de azúcar. Cultivos Tropicales. 2015;36(4):134–43.

7. Gauch HG, Hwang JT, Fick GW. Model evaluation by comparison of model-based predictions and measured values. Agronomy Journal. 2003;95(6):1442–6.

8. Rodríguez R, Puchadez Y, Abiche Maceo W, Tamayo M, Vázquez L, García H, et al. Software para la gestión de la información obtenida en el programa de mejoramiento de la caña de azúcar. Revista Cuba&Caña. 2012;(1):35–45.

9. Jorge H, González R, Casas M, Jorge I. Normas y procedimientos del programa de mejoramiento genético de la caña de azúcar en Cuba. PUBLINICA. La Habana, Cuba. 2011;308.

10. Rill S, Rodríguez S, Puchades D, Abiche Maceo W. C00-575 nueva variedad de caña de azúcar con alto potencial productivo. Revista Cuba&Caña. 2014;(1):7–11.

11. Wei X, Jackson P, Piperidis G, Parfitt R, Atkin F, Cox M. How well are the predicted breeding values of parental clones associated with family performance in the BSES-CSIRO sugarcane breeding program? International Sugar Journal. 2012;115(1371):208–11.

12. Hodge G. KeyNote 1: Use of best linear unbiased prediction in forest tree improvement and potential applications in plant breeding [Internet]. CAMCORE Cooperative, North Carolina State University, Campus Box 7626, Raleigh, NC 27695-7626, USA . [cited 2018 Apr 3]. Available from: www.sapba.co.za/uploads/files/conferences/2004/abstract_booklet.pdf

13. Piepho HP, Möhring J, Melchinger AE, Büchse A. BLUP for phenotypic selection in plant breeding and variety testing. Euphytica. 2008;161(1–2):209–28. doi:10.1007/s10681-007-9449-8

14. Zhao X, Liu Z, Dan F, Wang K. Plant breeding evaluation with rank entropy-based decision tree. IFAC-PapersOnLine. 2016;49(16):336–40. doi:10.1016/j.ifacol.2016.10.062

15. Zhou MM, Kimbeng CA, Tew TL, Gravois KA, Pontif M, Bischoff KP. Logistic regression models to aid selection in early stages of sugarcane breeding. Sugar Tech. 2014;16(2):150–6. doi:10.1007/s12355-013-0266-1

 

 

Recibido: 05/10/2017
Aceptado: 19/01/2018

 

 

Dr.C. Reynaldo Rodríguez-Gross, Grupo de Genética y Protección de Plantas. Estación Territorial de Investigaciones de la Caña de Azúcar Oriente Sur, Cuba. (22) 502254. Email: [e-mail]