ARTÍCULOS DE REVISIÓN

 

Sobre la aparición de la biomecánica y la mecanobiología computacional: experimentos computacionales y recientes hallazgos

About the appearance of Biomechanics and computation mechanobiology: computation experiments and recent findings

 

 

Diego A. Garzón-Alvarado^I; Carlos A. Duque Daza^II; Angélica María Ramírez Martínez^III

^IDepartamento de Ingeniería Mecánica y Mecatrónica. Facultad de Ingeniería. Universidad Nacional de Colombia.
^IIGrupo de Estructuras y Modelado de Materiales. Universidad de Zaragoza. España.
^IIIDepartamento de Ingeniería Mecánica. Fundación Universidad Central. Colombia.

 

 

---

RESUMEN

Procesos de desarrollo de órganos y remodelado de tejidos se ven influenciados por múltiples factores que van desde el componente biológico hasta la mecánica propia del sistema, donde cada uno de estos afecta en mayor o menor medida dependiendo del tipo de ente orgánico que se estudie. Desde esta perspectiva se ha desarrollado un nuevo campo de estudio de la bioingeniería denominado mecanobiología. Esta nueva área de trabajo involucra el estudio de modelos y la realización de experimentos con el ánimo de entender los procesos complejos que se dan en la génesis y mantenimiento de órganos y tejidos. Gracias a esta disciplina se ha logrado aislar y analizar diversos efectos como lo son la genética, los factores moleculares autocrinos y paracrinos, las cargas mecánicas sobre órganos y los efectos electromagnéticos. Con este conocimiento se han construido nuevos modelos matemáticos que pueden simular, de forma aproximada, el comportamiento in vivo. En este orden de ideas, el presente trabajo recoge las principales experiencias en el campo de la mecanobiología a nivel mundial, donde se han desarrollado trabajos que predicen la formación de huesos, el remodelado óseo, la formación y mantenimiento del cartílago articular, entre otros.

---

 

 

INTRODUCCIÓN

La ingeniería biomédica utiliza las diferentes metodologías habituales en el ámbito ingenieril: ensayos de laboratorio y en campo y simulación computacional. Esta última precisamente está teniendo un avance vertiginoso gracias al desarrollo y mejora continua de los computadores, siendo hoy en día una potente herramienta utilizada habitualmente en el diseño de prótesis (figura 1), seguimiento de patologías y en la conceptualización del comportamiento de tejidos y procesos biológicos. En esta área de investigación en particular se construyen algoritmos complejos capaces de predecir el comportamiento del cuerpo humano ante distintas condiciones mecánicas,¹ eléctricas,² y magnéticas.³ Además, la simulación computacional permite estudiar nuevas teorías sobre procesos biológicos con objeto de establecer nuevas líneas de experimentación y modelos más adecuados para fenómenos tan complejos como la marcha humana, la angiogénesis, la formación de tumores (figura 2), la morfogénesis y el crecimiento biológico, entre otros muchos casos.⁴

El uso continuo de la simulación en medicina ha permitido obtener datos importantes acerca del comportamiento biológico, mecánico y químico de órganos y tejidos utilizando la formalización matemática y la consiguiente simulación numérica de procesos biológicos muy complejos. Distintos problemas de medicina relacionados con la cirugía, el trauma y la rehabilitación han sido identificados, conceptualizados y sistemáticamente resueltos numéricamente. Sin embargo, aunque la simulación numérica en bioingeniería es de reciente desarrollo, la abstracción física y la consiguiente formulación matemática del cuerpo humano se remontan a varios siglos atrás.

Uno de los primeros científicos en conceptualizar mediante modelos matemáticos los fenómenos fisiológicos fue Galileo Galilei. Éste (Pisa, 15 de febrero de 1564 - Florencia, 8 de enero de 1642),⁷ considerado el "padre de la ciencia", incursionó en casi todas las áreas de la ciencia y las artes, y la medicina no fue la excepción. A partir de sus observaciones sistemáticas, Galileo midió el ritmo cardíaco por comparación de éste con los sucesivos sonidos de un péndulo sincrónico.

Utilizando los principios de medida de Galileo, William Harvey (1 de abril de 1578, 3 de junio de 1657)7 describió las propiedades de la sangre al ser distribuida por todo el cuerpo a través del bombeo del corazón. Esto confirmó las ideas de René Descartes que en su libro "Descripción del cuerpo humano" afirmó que las arterias y las venas eran tubos que transportaban nutrientes alrededor del cuerpo7. Debe apuntarse que el español Miguel Servet describió la circulación pulmonar un cuarto de siglo antes que Harvey naciera, por lo que en el libro de Teología (Christianismi Restitutio, publicado en 1553) que fue considerado hereje. En consecuencia, casi todas las copias del mismo fueron quemadas, excepto tres que fueron descubiertas décadas más tarde.⁸

Otro colega de Galileo, Santorio Santorio estudió el fenómeno denominado "perspiratio insensibilis"(la pérdida de agua en el cuerpo), para lo cual usó una báscula especial de su invención. En el transcurso de algunos años, Santorio registró escrupulosamente el peso del cuerpo en las diferentes horas del día, para medir el balance hídrico, llegando a conclusiones sorprendentemente cercanas a la realidad, si se considera la simplicidad de los instrumentos de que disponía.⁷

Descartes (31 de marzo, 1596, La Haye en Touraine - 11 de febrero, 1650, Estocolmo) sugirió que los sistemas físicos, incluido el cuerpo humano, eran regidos por las mismas leyes universales.⁷

Leonhard Euler (15 de Abril, 1707 - 7 de Septiembre, 1783) utilizó las leyes de Newton (quien escribió sobre el movimiento, pero no sobre biomecánica) para obtener las ecuaciones diferenciales necesarias para describir la propagación de ondas en arterias, investigación que consignó en un articulo publicado en 1775.⁹

Thomas Young (13 de Junio, 1773 - 10 de Mayo, 1829) estudió la formación de la voz humana, la cual identificó con un modelo de elasticidad de materiales. Young también trabajo en la teoría sobre la luz y el color, lo cual le permitió desarrollar lentes para el astigmatismo.

Hermann Ludwig Ferdinand von Helmholtz (31 de agosto, 1821 - 8 de septiembre, 1894) es considerado el padre de la bioingeniería. Helmholtz fue profesor de fisiología y patología en diversas universidades, para dedicar sus últimos años a la enseñanza de la física en la Universidad de Berlín. Sus contribuciones abarcan la óptica, acústica, termodinámica, electrodinámica, fisiología y medicina. A partir de sus múltiples conocimientos en fisiología y física, Helmholtz diseñó lentes, calculó la geometría del ojo humano, estudió el mecanismo de audición, determinó la velocidad de un pulso nervioso y mostró que el latido cardíaco es una importante fuente de calor.

Entrando ya en el siglo XX se encuentran numerosos aportes a la concepción matemática del cuerpo humano, entre los que cabe destacar a Archibald Vivian Hill (26 de septiembre de 1886 - 3 de junio de 1977), fisiólogo inglés, fundador de la biofísica, ganador en 1922 del premio Nobel de medicina por sus descubrimientos sobre el funcionamiento del sistema muscular, y a quien se debe la, hoy en día famosa, ecuación de Hill utilizada en múltiples campos del modelado biológico (ver por ejemplo¹⁰). Por su parte, la construcción de modelos matemáticos de auto-organización se debe a Alain Turing (23 de Junio, 1912 - 7 de Junio, 1954), quien en 1952 propuso la autoformación de patrones espaciales a partir de ecuaciones de reacción-difusión, fenómeno que fue comprobado experimentalmente 40 años después, cuando la reacción conocida como CIMA (reacción entre los iones clorito y yoduro en presencia de ácido malónico) conformó patrones de concentración en pruebas de laboratorio.¹¹

Durante el siglo XX se confirmaron diversas tendencias en la simulación en bioingeniería, específicamente en la simulación de las funciones y comportamiento del cuerpo humano ante agentes biofísicos externos. La biomecánica y la mecanobiología, son dos de estas importantes áreas de investigación actual.¹² La biomecánica se ha encargado de responder a las preguntas sobre el comportamiento de las diversas estructuras corporales ante diferentes condiciones de carga. Por su parte, la mecanobiología responde a las preguntas que surgen sobre la diferenciación, mantenimiento y adaptación de las células como una respuesta activa a los estímulos biomecánicos de su entorno.

Es así como en este artículo se describe el estado del arte y los principales trabajos en el área de biomecánica, tema que se trata en el primer apartado, y las principales contribuciones en la Mecanobiología, tema de la segunda parte. Por último se hace una breve discusión sobre estas dos nuevas ramas de la ingeniería biomédica y de la medicina.

 

La biomecánica computacional: Una respuesta a las preguntas ortopédicas

La biomecánica surge de la necesidad de responder preguntas y hallar soluciones a problemas médicos y biológicos que involucran el conocimiento de la mecánica, la geometría y los materiales.⁷La biomecánica ha tenido un vertiginoso avance, desde su origen, con Galileo Galilei, quien estudió el ritmo cardiaco7, hasta nuestros días, donde se realizan sofisticados estudios de nanotubos de carbono como andamios estructurales para acelerar y mejorar el proceso de recuperación de fracturas.¹³ Es así como la biomecánica, a su vez, se ha bifurcado en dos grandes ramas, a saber, la biomecánica experimental y la computacional, esta última, área del conocimiento en que se ubica el presente trabajo.

En el año de 1968 se crea el Journal of Biomechanics, revista de alto nivel de impacto (indexado como JCR), en la que se publican los primeros artículos de la biomecánica computacional. Tal vez, el primer artículo que relata el uso del computador se encuentra en,¹⁴ el cual modeló el sistema arterial humano en un computador análogo, en donde se estudió la evolución de la presión arterial y las ondas de flujo ejercidas por los pulsos de presión durante el latido del corazón. Desde de la década de los 60's se han hecho simulaciones de todo tipo, desde el sistema musculoesquelético^15-18 hasta problemas de cargas sobre tumores. Hoy en día (año 2009) se realizan modelos computacionales tan específicos como en 19, donde se emplea mecánica computacional de fluidos, técnicas de malla deformable e interacción fluido-estructura para estudiar los movimientos del cilio activo y la respuesta del cilio pasivo ante diferentes tipos de flujos. El objeto de este estudio es entender el método de cuantificación del patrón de flujo en el nodo de un embrión de mamífero que regula la aparición del lado izquierdo del cuerpo en desarrollo (es decir, señala la ubicación de los órganos, específicamente el corazón).

La biomecánica computacional ha servido en múltiples áreas de la medicina aplicando la mecánica como herramienta de análisis. Sin embargo, la mayor aplicación de esta área ha sido en solucionar problemas ortopédicos y entender el sistema musculoesquelético. Es así como se crean varios grupos de investigación en el mundo, cuyos principales investigadores son Dennis Carter del grupo de biomecánica de Stanford University (Estados Unidos)20, Peter Hunter del grupo bioingeniería de la University of Auckland (Nueva Zelanda),²¹ Stephen Cowin del City College de Nueva York (Estados Unidos),²² Rik Huiskes de la división de Ingeniería Biomédica de la Universidad Técnica de Eindhoven (Holanda),²³ Manuel Doblaré del grupo de Estructura y Modelado de Materiales de la Universidad de Zaragoza (España),²⁴ entre otros. En estos grupos la investigación en biomecánica se ha dividido específicamente en simulación de músculo, tendones y ligamentos (también denominados tejidos blandos) y simulación de hueso (tejido duro). Además, se han realizado, en menor medida, otras simulaciones como son modelos de corazón, venas y arterias (que esta enmarcado en tejido blando) e investigación celular (mecánica celular) (ver figura 3).

Obsérvese que en cualquiera de las dos macroáreas de la biomecánica, se presentan grandes ramas como son la mecánica de fluidos, análisis de movimiento y el análisis de tensiones o mecánica de sólidos. Es de resaltar, también, que la parte computacional y la experimental están en una continua sinergia para generar nuevos y mejores modelos de explicación de fenómenos biológicos y médicos.

La figura 3, muestra la interacción entre las diferentes áreas de la biomecánica, experimental y computacional, y las herramientas de análisis utilizadas para estudiar el cuerpo humano. Se observa entonces como las herramientas de la mecánica clásica, como son la mecánica de fluidos, mecánica de sólidos y el análisis de movimiento son utilizados para entender el comportamiento de diferentes tejidos (y órganos) como el tejido blando, duro y la mecánica celular. El análisis de tejido duro ha sido el más estudiado desde el punto de vista computacional. Para ello se usa la elasticidad y conceptos de mecánica de sólidos avanzada, como la viscoelasticidad, hiperelasticidad y plasticidad (mecánica de sólidos no lineal). Los métodos de solución de estos modelos de mecánica de sólidos utiliza, en general, el de los elementos finitos. La introducción de los métodos computacionales, específicamente los elementos finitos, a la biomecánica ortopédica se inicia en 1972,²⁵ año en el que comienzan las publicaciones sobre evaluación de esfuerzos en huesos humanos. Desde este año la frecuencia de publicaciones sobre estructuras óseas, hueso-prótesis, mecanismos de fijación de fracturas y su relación con otros tejidos aumento exponencialmente.²⁵ Los objetivos de las investigaciones realizadas fueron establecer relaciones entre las cargas y la morfología de huesos, y establecer diseños óptimos para fijaciones, prótesis y mejorar las técnicas de implantes.²⁵

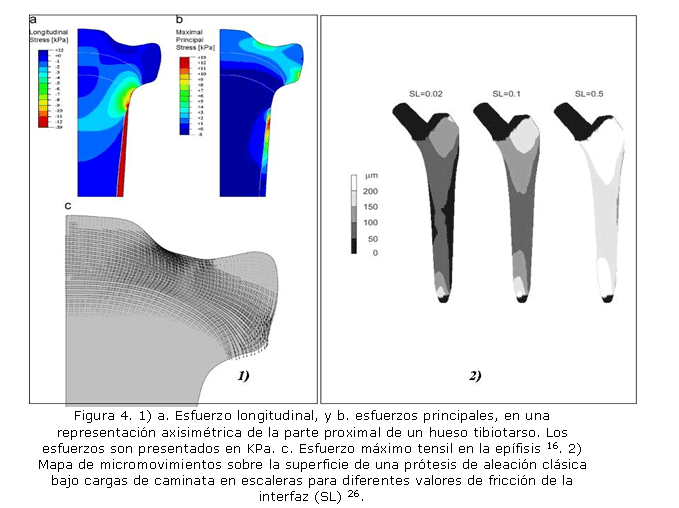
En un artículo publicado,¹⁶ por ejemplo, se evalúan los esfuerzos inducidos sobre el cartílago por la tensión del periostio. El objetivo es entender si la liberación de carga de compresión en el cartílago en fase de crecimiento permite modular el desarrollo de los huesos largos (ver figura 4a). Otro ejemplo de análisis de tejido duro y prótesis realizado por elementos finitos (EF) se encuentra en otro artículo,²⁶ donde se observa el modelo por EF de una prótesis de cadera. En esta documento²⁶ se estudian los micromovimientos en la interfaz prótesis-fémur y su asociación con la inestabilidad del implante (ver figura 4b). El objetivo del trabajo es evaluar las prótesis sin cemento y relacionar el micromovimiento con el dolor reportado por pacientes cuando se inicia la pérdida de fijación. Abdul-Kadir y colaboradores²⁶ encontraron que la interferencia mecánica de 50 ?m es suficiente para alcanzar una buena fijación primaria y evitar fracturas en el fémur.

Sin embargo, el método de los elementos finitos no ha sido el único utilizado en la biomecánica computacional. En un artículo²⁷ se muestra la aplicación del método de los elementos de contorno para simular el desgaste de la prótesis de cadera. En este artículo se hacen simulaciones para diferentes tamaños de fémur, tipos de copas acetabulares y tipos de material. Bajo estas condiciones se colocan cargas mecánicas de caminata normal y se simula el comportamiento de los materiales durante 20 años de servicio. Este trabajo muestra la utilidad de los elementos de contorno para almacenar grandes cantidades de información en el tiempo de simulación y la gran utilidad para hacer análisis de elasticidad. La conclusión del estudio muestra, después de 20 años de operación normal, que el deterioro de la copa acetabular puede llegar a 1.7 mm de profundidad, lo cual puede ser perjudicial al sistema implante-hueso por la generación de partículas del desgaste, a los cuales, el cuerpo puede generar una reacción inmune que termina con la fijación de la prótesis.

 

En el año de 1978, Stephen Cowin del Departamento del City College de Nueva York publica,²⁸ artículo que desarrolla el proceso de remodelamiento óseo utilizando un algoritmo adaptativo (de control) que predice la densidad del tejido a partir de las tensiones que soporta el hueso. La teoría de remodelamiento óseo fue programada bajo elementos finitos, usando un control retroalimentado a partir de la densidad de energía de deformación, el cual lograba determinar la adaptación de forma y densidad del hueso ante diferentes requerimientos de carga mecánica, resultados que confirmaban la teoría de adaptación del hueso expuesta por Wolff y Roux (1881).²⁹ Este trabajo abre un debate importante entre diferentes teorías expuestas por Huiskes,³⁰ Carter,³¹ Doblaré³² y otros muchos exponentes que intentan predecir el comportamiento adaptativo del hueso a partir de la teoría de control y de plasticidad, entre otros.

En otro artículo publicado³³ se describe uno de los tantos algoritmos que se han desarrollado para explicar el proceso de remodelación ósea. En la figura 6a) se muestra la optimización topológica como herramienta para predecir la adaptación del tejido óseo a partir de la minimización de la masa total, utilizando la maximización de la resistencia del mismo. A partir de la teoría de remodelación, se dio inicio al análisis del comportamiento del tejido a partir de cargas impuestas por endroprótesis ³⁴ (ver figura 6b), por lo cual se abandonó la idea de analizar los esfuerzos sobre el material de la prótesis para volver sobre lo que ocurría al nivel de tejido, éste adelanto sirvió para predecir la distribución trabecular durante el uso continuo de los implantes a lo largo del tiempo. En la figura 6b) se muestra, por ejemplo, la forma en que remodela el hueso aledaño al implante de cadera cuando llega al estado estable de uso. Se puede observar que el tejido pierde densidad gracias a la inadecuada transferencia de carga al fémur, muestra de ello es la pérdida de la región calcar como se ha reportado en la literatura.^33,34

Es así como nace la mecanobiología, la cual establece la relación del comportamiento del tejido desde el punto de vista biológico, a partir de las cargas mecánicas. La Mecanobiología, fue el término acuñado por Rik Huiskes,^12,35 la cual conformó una nueva rama de la bioingeniería, que será explicado en el siguiente capítulo (Fig. 6).

La mecanobiología computacional: Como se comporta el tejido ante cargas mecánicas?

La mecanobiología computacional, determina las reglas cuantitativas que gobiernan las acciones celulares para su expresión, diferenciación y mantenimiento ante estímulos biológicos y mecánicos, las cuales pueden simularse mediante métodos numéricos. El procedimiento para hallar dichas reglas es habitualmente mediante el proceso de "prueba-error". ¹² Los ensayos computacionales se simulan a partir de problemas de valor en el contorno mediante los cuales, las cargas mecánicas sobre el contorno son trasladadas a variables mecánicas locales (deformaciones y tensiones). Del lado biológico, estas variables mecánicas locales o biofísicas estimulan la expresión celular para regular, por ejemplo, la composición de la matriz y la expresión de sustancias moleculares. Tanto la parte biológica como la mecánica se combinan en un modelo computacional, que considera la aplicación de fuerzas, mecanotransducción, expresión celular, genética y la transformación de las características de la matriz extracelular. El método usual de implementación numérica de estos problemas mecanobiológicos es el método de los elementos finitos.^36,37

A diferencia de los problemas tradicionales de la ingeniería, donde el cálculo numérico produce una respuesta a un fenómeno conocido, en la mecanobiología se ensayan diferentes relaciones matemáticas, variables de entrada y estímulos biofísicos para simular el comportamiento de un tejido u órgano. De esta forma se establecen hipótesis, y su correspondiente simulación permite verificar si es plausible o no a la luz de las evidencias experimentales existentes que muchas veces son incompletas e insuficientes para verificar, sin duda alguna, las hipótesis de partida, abriéndose entonces nuevas vías de experimentación.^36,38 Por ello, la simulación numérica ha sido recientemente citada como "El tercer método de la ciencia", después de la lógica (teórica) y la experimentación.³⁹

Uno de los temas más importante en la mecanobiología es la mecanotransducción, concepto que ronda en la comunidad científica desde Roux en 188 129 hasta las últimas publicaciones sobre el tema.⁴⁰ Usando las herramientas científicas ya descritas, en los últimos años, se ha intentado predecir el crecimiento y la diferenciación celular en términos cuantitativos, a partir de estímulos biofísicos y mecánicos.

El crecimiento biológico es el proceso mediante el cual se adiciona masa, se configura la forma, y se ajustan las dimensiones finales de los órganos que se encuentran en desarrollo. En el proceso de crecimiento del cuerpo humano se encuentran dos tipos de tejidos: el tejido duro y el tejido blando. El tejido duro puede desarrollarse mediante la aposición de masa sobre la superficie del tejido (desarrollo intramembranoso), o mediante el proceso de formación de un molde de cartílago y posterior reemplazo por tejido óseo, como ocurre en el caso de los huesos largos (desarrollo endocondral). Por el contrario, los tejidos blandos, como los vasos sanguíneos o ligamentos, experimentan un crecimiento volumétrico que genera tensiones residuales internas sobre los órganos. La cinemática del crecimiento fue descrita inicialmente por Skalak et al.,⁴¹ y ha sido desarrollada extensamente por muchos otros autores, entre los que se pueden contar Cowin,²⁹ Doblaré y García-Aznar⁴² y Humphrey.⁴³ Por ejemplo, Kuhl y Steinmann han presentado un modelo teórico y numérico de crecimiento a partir de un sistema termodinámico abierto que tiene aplicación a tejidos duros⁴⁴ y para la consolidación de heridas⁴⁵. Por su parte, Garikipati et al.⁴⁶ proponen una formulación completa para el transporte de masa y mecánica multifásica en tejidos, incluyendo crecimiento.

Los modelos antes mencionados^41,29,42-46 se construyeron a partir de la evidencia fenomenológica de que el crecimiento es inducido por estímulos mecánicos. Una línea diferente de trabajo fue abierta a partir de los trabajos de Turing,⁴⁷ donde se pone de manifiesto que las señales moleculares generan estímulos sobre las células para que éstas sinteticen matriz extracelular, se dividan o se diferencien, según reglas biológicas que inducen el crecimiento de tejidos y órganos.⁴⁸

Los modelos de crecimiento, a partir de la información biológica (señales moleculares y respuesta celular) han merecido un especial interés a partir del trabajo de Turing.⁴⁷ De hecho, éste demostró el potencial de las ecuaciones de reacción-difusión para generar patrones espaciales de las sustancias bioquímicas que, bajo reglas particulares de diferenciación, permiten la formación de tejidos y la agrupación de células. La evolución de estos modelos bioquímicos ha traído consigo el desarrollo de disciplinas asociadas tan importantes como los sistemas dinámicos biológicos. A partir de los primeros modelos de Turing se han construido formulaciones matemáticas de muchos procesos biológicos basados en este esquema.⁴⁷

Las primeras ecuaciones de reacción-difusión tenían en cuenta una única especie química, como en el trabajo de Wolpert⁴⁹ donde se muestra que la posición molecular de una sustancia permite la diferenciación celular dependiente de un nivel umbral de concentración establecido. A medida que la comprensión de los fenómenos bioquímicos aumentaba, se fueron construyendo modelos complejos con múltiples especies.

Cada uno de estos modelos matemáticos genera patrones particulares según los parámetros involucrados en la ecuación. Los sistemas dinámicos han jugado desde entonces un papel importante en biología, intentando predecir las bifurcaciones y la formación de patrones, según tres posibilidades de inestabilidad: Hopf, Inestabilidad de Turing y Turing Oscilante.⁵⁰

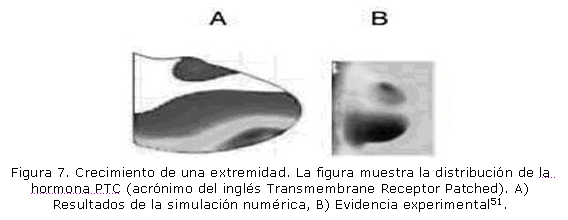
En lo que se refiere en concreto a la formulación bioquímica del crecimiento biológico, también se han construido diversos modelos. Por ejemplo, Dillon et al.⁵¹ simularon el desarrollo de extremidades incorporando el crecimiento celular, la mitosis y las interacciones de los morfogenes producidos en la zona de actividad apical (figura 7). De otro lado, Anotida Madzvamuse⁵² simuló la distribución de la pigmentación en las alas de mariposas, explicando, mediante modelos de reacción-difusión, los múltiples tipos de distribución dependiendo del tamaño y forma del dominio de análisis (figura 8). También se ha simulado, mediante las ecuaciones de reacción-difusión, el movimiento celular inducido por sustancias químicas (quimiotaxis), que es conocido en un gran número de situaciones, homeostáticas y patológicas.^53-58 La quimiotaxis ha explicado la formación de agregaciones celulares como resultado de la respuesta de éstas a gradientes químicos.⁵⁹

Posteriormente, a principio de la década de los 80, Oster y Murray⁶⁰ construyeron un modelo mecanobiológico que constituyó la unión entre el modelo de reacción difusión con las cargas mecánicas. A partir de este modelo se han simulado procesos de condensación mesenquimal que incluyen procesos biológicos y mecánicos. Bajo este marco de trabajo, se han simulado diferentes casos como la formación de tumores,^61,62 la formación de extremidades, la tubulogénesis y la angiogénesis. Un ejemplo reciente lo describe Namy et al.⁵⁹ en donde se determinan las condiciones críticas del espacio de parámetros del modelo para que se produzca la tubulogénesis en un tejido sometido a campos de tracción celular en una caja de Petri (figura 9).

Paralelamente a la anterior tendencia, y a partir de la evidencia experimental, se crearon modelos donde las cargas mecánicas influenciaban la formación de tejidos, pero que, a diferencia de los modelos antes descritos, no incluían ecuaciones de reacción difusión de sustancias químicas. Los modelos basados en esta línea de la mecanobiología han significado un avance importante en la explicación de fenómenos relacionados con el cuerpo humano, especialmente con el sistema esquelético¹² (figura 10), porque además de explicar los procesos biológicos permiten desarrollar líneas de experimentación mecánica basadas en los ensayos numéricos.¹² Ejemplos sobre esta línea de acción han sido publicados en las últimas dos décadas. Por ejemplo, Carter et al⁶³ citan la aparición de los centros secundarios de osificación en función de una variable auxiliar denominada "´índice osteogénico", que está relacionada con los valores de la tensión octaédrica a la que se encuentra sometido el hueso. A partir de ensayos numéricos, y por comparación con las evidencias experimentales, se hallaron intervalos posibles para la variable osteogénica. Utilizando la misma metodología mecanobiológica, se ha simulado la reparación de fracturas óseas⁶⁴ donde se han considerado estados de crecimiento, diferenciación y regeneración tisular regulados a través de factores exclusivamente mecánicos.

Por otro lado, y a partir de datos clínicos y de experimentación, se han desarrollado diversos modelos sobre la influencia mecánica y genética en la morfogénesis y la osificación endocondral durante la etapa embrionaria. En especial, se han desarrollado modelos sobre la formación femoral en etapa prenatal, donde aún no se considera la formación del centro secundario de osificación 65. Shefelbine et al^66,67 han descrito las consecuencias mecánicas de la mineralización sobre el comportamiento de la placa de crecimiento. Además, a partir de las condiciones mecánicas del desarrollo, Shefelbine66 propone un modelo sobre la evolución del ángulo bicondilar, mostrando datos importantes sobre la evolución estructural del esqueleto del hombre y las diferencias con los primates.

Van Donkelaar y Huiskes68 crearon un modelo que está a mitad de camino entre los de reacción-difusión y los modelos mecánicos. En un marco de trabajo unidimensional, realizaron un modelo de elementos finitos que incorpora el crecimiento de un hueso por señales moleculares presentes en la metáfisis de un fémur humano. El análisis incluye síntesis de factores de crecimiento en zonas relevantes del hueso en formación, así como el transporte y degradación de dichas sustancias.

Aunque se ha estudiado la formación de tejidos, la formación completa de órganos es aún un tema de investigación activo.⁶⁹ Por ello, para aislar fenómenos y variables del entorno de un tejido, o un órgano, se utiliza la Mecanobiología como fuente experimental "in mente" a partir de leyes básicas de conservación. Hoy en día se ha dado un paso más en la investigación, por lo que el acercamiento computacional de procesos celulares y moleculares a nivel multiescala es fundamental en el nuevo desarrollo de la mecanobioquímica computacional, tema central de grupos de investigación de CalTech (Estados Unidos),⁷⁰ National Institute of Health (Estados Unidos),⁷¹ Universidad de Delaware (Estados Unidos),⁷² entre otros.

 

DISCUSIÓN Y CONSIDERACIONES FINALES

La aparición de la biomecánica se da para entender fenómenos mecánicos que ocurren e en el cuerpo, y específicamente, para comprender el movimiento, la estructura (y forma) y la mecánica de fluidos de líquidos corporales. Sin embargo, la realización de experimentos complejos que involucran seres humanos puede incurrir en problemas éticos que se debieron solucionar, en su momento, con el computador, por esto, la biomecánica computacional hace su aparición para fomentar nuevas líneas de investigación biomédica. Por su parte, la Mecanobiología surge para intentar discernir, de forma plausible, sobre procesos biológicos y físicos, de alta complejidad, cuya experimentación esta lejos de los recursos actualmente existentes.

Por tanto, la pregunta central del problema es: ¿se pueden llevar a cabo ensayos computacionales de fenómenos a nivel de tejido y órgano sin conocer exactamente los parámetros y variables implicadas?. La respuesta a esta pregunta es tal vez la contradicción central a la Mecanobiología computacional. Muchos de los fenómenos biológicos que involucran cargas tienen variables aún no muy bien entendidas, por tanto, la Mecanobiología esta jalonando nuevas líneas de experimentación, que en un futuro pueden dar respuestas sobre valores y modelos que son supuestos en el computador. El tiempo lo dirá.

Sin embargo, aún bajo las contradicciones enunciadas, hay fenómenos mecanobiológicos que son simulados y corresponden, cualitativamente, a lo observado clínica y experimentalmente. Es allí donde la Mecanobiología ha realizado importantes avances. Por ejemplo, en la estimación de variables y parámetros desconocidos (en las relaciones existentes entre diferentes modelos a nivel molecular y celular) se cuenta hoy en día con nuevos y valiosos datos para alimentar modelos que pueden predecir fenómenos como el crecimiento del cáncer, el crecimiento de huesos largos y fenómenos de reparación ósea.

Es de notar que los procesos biológicos presentan una gran variabilidad estadística, por lo que los modelos mecanobiológicos pueden ser, simplemente, estimaciones gruesas de fenómenos que involucran procesos multiacoplados. Este acoplamiento de fenómenos trae consigo el manejo de diferentes escalas de tiempo y espacio, lo cual ha desarrollado nuevas ramas que utilizan modelos "multiescala", que tal vez, especulando, puede ser el siguiente paso en la comprensión de la física, biología y los materiales.

En este artículo se hizo una breve revisión del estado del arte de la biomecánica y Mecanobiología, se citan algunas fuentes y se describen los modelos más importantes y relevantes a juicio de los autores. Sin embargo, por ser una línea de investigación activa, los artículos que se publican al respecto pueden ascender a los cientos de miles, por lo que la visión entregada aquí es minúscula con respecto al gran universo de producción científica sobre el área. Por tanto, este artículo se espera sea la motivación para iniciar nuevos trabajos en nuestro país, en pro de solucionar problemas biomédicos propios de nuestro entorno.

 

CONCLUSIONES

Se ha realizado un breve recorrido sobre la historia de la biomecánica y su trascurrir hacia la Mecanobiología como herramientas necesarias para el análisis médico, y en especial, ortopédico. En el artículo se puede evidenciar que el advenimiento de la computación permitió desarrollar teorías más sofisticadas y claras sobre los fenómenos biológicos que ocurren a nivel de tejido y órgano. Es así, como aplicando las leyes fundamentales de conservación: de masa, momentum, energía y sobre la base del principio de entropía se establecen relaciones biológicamente plausibles para formular modelos computacionales que describen procesos biológicos.

Por tanto, se puede concluir que los nuevos recursos computacionales (las nuevas herramientas) y los nuevos métodos de simulación (entre los que se cuenta los métodos numéricos) deben interactuar con los hallazgos biológicos y médicos para permitir construir nuevos métodos de análisis para mejorar la predicción, análisis y diseño de nuevos tratamientos y dispositivos para pacientes con problemas ortopédicos y que requieran tratamiento de rehabilitación. Esta nueva ciencia es, sin duda, una nueva herramienta para mejorar las condición de vida de los pacientes con trauma y patologías ortopédicas.

 

REFERENCIAS BIBLIOGRÁFICAS

1. D. R. Carter, B. Mikic, and K. Padian. Epigenetic mechanical factors in the evolution of long bone epiphyses. Zoological Journal of the Linnean Society. 1998. 123(2):163-178.
2. W.D. Greason. Methodology to simulate speed of approach in electrostatic discharge. Electrical Overstress/Electrostatic Discharge Symposium. 1997. Proceedings 23-25:125 - 132
3. Ovidiu Rotariu, and Norval JC Strachan, Modelling Magnetic Carrier Particle targeting in the Tumor Microvasculature for Cancer Treatment, JMMM. 2005. 293: 639-646.
4. J. Enderle, S.M. Blanchard, and J. Bronzino. Introduction to Biomedical Engineering. Ed. Elsevier Academic Press, 1992:1-125.
5. Yang, J., Peña, E., Abdel-Malek, K., Patrick, A., Lindkvist. A multifingered hand prosthesis next term. Mechanism and Machine Theory. 2004.39(6). 555-581.
6. Clatz, O., Bondiau, P., Delingette, H., Sermesant, M., Warfield, S., Malandain, G. Ayache, N. Brain tumor growth simulation. 2004. Research Report. INRIA, 5187: 1-20
7. Y.C. Fung. Biomechanics: Mechanical properties of living tissues. Ed. Springer Verlag, 1990.
8. Debus, A.G. El hombre y la naturaleza en el renacimiento. Reporte FCE-CONACYT 384, México, 1985: 1-15.
9. V.S. Varadarajan. Euler Through Time: A new look at old themes. Ed. AMS, 1983:1-100.
10. J.E.M. Brouwers, C.C. van Donkelaar, B.G. Sengers, and Huiskes R. Can the growth factors PTHrP, Ihh and VEGF, together regulate the development of a long bone? Journal of Biomechanics. 2006. 39:2774-2782
11. I. Lengyel and I.R. Epstein. Modeling of Turing structures in the chloriteiodide- malonic acid-starch reaction system. Science. 1991. 251:650-652.
12. M.C.H. van der Meulen and R. Huiskes. Why mecanobiology? Journal of Biomechanics 2002. 35(4): 401-414.
13. Edwards, S.L., Church, J.S., Werkmeister, J.A., Ramshaw, J.A.M. Tubular micro-scale multiwalled carbon nanotube-based scaffolds for tissue engineering. Biomaterials. 2009. 30(9): 1725-1731.
14. Snyder, M.F., Rideout, V.C., Hillestad, R. J. Computer modeling of the human systemic arterial tree. Journal of Biomechanics. 1968. 1(1). 341-353.
15. Fox, M.D., Reinbolt, J.A., Õunpuu, S., Delp, S. Mechanisms of improved knee flexion after rectus femoris transfer surgery. Journal of Biomechanics. 2009. 42(5): 614-619.
16. Liu, X.S., Bevill, G., Keaveny, T.M., Sajda, P., Guo, X.E. Micromechanical analyses of vertebral trabecular bone based on individual trabeculae segmentation of plates and rods. Journal of Biomechanics. 2009. 42(3). 249-256.
17. Eswaran, S.K., Bevill, G., Nagarathnam, P., Allen, M.R., Burr, D., Keaveny, T. Effects of suppression of bone turnover on cortical and trabecular load sharing in the canine vertebral body. J. Biomech 2009. 42(4):517-23.
18. Huthmann, S., Staszyk, C., Jacob, H.-G., Rohn, K., Gasse, H. Biomechanical evaluation of the equine masticatory action: Calculation of the masticatory forces occurring on the cheek tooth battery. Journal of Biomechanics. 2009. 42(1): 67-70.
19. Chen, D., Norris, D., Ventikos, Y. The active and passive ciliary motion in the embryo node: A computational fluid dynamics model. J Biomech. 2009; 42(3):210-6.
20. Grupo de Biomecánica de la Universidad de Stanford. Disponible en: http://biomechanical.stanford.edu/Main_Page
21. Grupo de Biomecánica de la Universidad de Auckland. Disponible en: http://www.bioeng.auckland.ac.nz/
22. Grupo de sistema musuculoesqueletico de la Universidad de Utah. Disponible en: http://mrl.sci.utah.edu/
23. Grupo de Biomecánica de la Universidad de Eindhoven. Disponible en: http://www.mate.tue.nl/mate/peopleinsection.php/4
24. Grupo de Estructuras y modelado de materiales de la Universidad de Zaragoza. Disponeble en: http://i3a.unizar.es/gemm/
25. Huiskes, R., Chao, E.Y.S. A survey of finite element analysis in orthopedic biomechanics: The first decade. Journal of Biomechanics. 1983. 16(6). 385-409.
26. Abdul-Kadir, M., Hansen, U., Klabunde, R., Lucas, D., Amis, A. Finite element modelling of primary hip stem stability: The effect of interference fit. Journal of Biomechanics. 2008. 41(3):587-594.
27. Sfantos, G.K., Aliabadi, M.H. Total hip arthroplasty wear simulation using the boundary element method. Journal of Biomechanics. 2007. 40(2): 378-389.
28. Cowin, S.C., Van Buskirk, W. C.Internal bone remodeling induced by a medullary pin. Journal of Biomechanics. 1978. 11(5): 269-275.
29. Cowin, S. Bone Mechanics Handbook. CRC press LLC, 2001: 20-100.
30. Weinans, H., Huiskes, R., Grootenboer, H.J. The behavior of adaptive bone-remodeling simulation models. Journal of Biomechanics. 1992. 25(12): 1425-1441.
31. Jacobs, C.R.m Simo, J.C., Beaupre, G.S., Carter, D.R. Adaptive bone remodeling incorporating simultaneous density and anisotropy considerations. Journal of Biomechanics. 1997. 30(6): 603-613.
32. Doblaré, M., Garc??a, . Anisotropic bone remodelling model based on a continuum damage-repair theory. Journal of Biomechanics. 2002. 35(1): 1-17
33. Garzón-Alvarado, D.A. Análisis del Proceso de Regeneración Ósea por el método de los elementos finitos. Tesis de Maestría. Universidad Nacional de Colombia. 2003: 1-200.
34. Garzón-Alvarado, D.A., Roa, M., Ramírez, A. Predicción Del Proceso De Remodelación Ósea Para Diferentes Implantes De Cadera Utilizando Optimización Topológica. Revista Cubana de Ortopedia. . 2009. 22(2). Online.
35. Mechanobiology of the skeleton. Turner CH, Warden SJ, Bellido T, Plotkin LI, Kumar N, Jasiuk I, Danzig J, Robling AG. Sci Signal. 2009; 2(68):pt3.
37. P.J. Prendergast. Finite element models in tissue mechanics and orthopaedic implant design. Clinical Biomechanics. 1997. 12(6):343-366.
38. Huiskes, R., 1995. The law of adaptive bone remodeling: a case for crying newton?. In: Odgaard, A. and Weinans, &H., Editors, 1995. Bone Structure and Remodeling, World Scientific Publishing, Singapore, River Edge, London, pp. 15-24.
39. Kevin Kelly. The Third Culture. Science. 279: 992-993
40. I. Martin, S. Miota, A. Barberoa, M. Jakoba, and D. Wendt. Osteochondral tissue engineering. Journal of Biomechanics. 2007. 40(4): 750-765
41. G. Skalak, M. Dasgupta, E. Moss, and P. Otten. Analytical description of growth. Journal of Theoretical Biology. 1982. 94(3): 555-577.
42. Doblaré, M., García-Aznar, J.M. On the numerical modeling of growth, differentiation and damage in structural living tissues. Arch. Comput. Meth. Engng. 2006. 13(4): 471-513.
43. J.D. Humphrey. Mechanics of arterial wall: review and directions. Crit Rev Biomed Eng. 1995; 23(1-2):1-162.
44. E. Kuhl and P. Steinmann. Theory and numerics of geometrically non-linear open system mechanics. Int. J. Numer. Metho. Engng. 2003; 58(11): 1593-1615.
45. E. Kuhl and P. Steinmann. Computational modeling of healing; an application of the material force method. Biomech. Model. Mechanobiol. 2004 2(4):187-203.
46. K. Garikipati, E.M. Arruda, K. Grosh, H. Narayanan, and S. Calve. A continuum treatment of growth in biological tissue: the coupling of mass transport and mechanics. Journal of the Mechanics and Physics solids, 2004. 52(7): 1595-1625.
47. A. M. Turing. The chemical basis of morphogensis. Phil. Trans. R. Soc. Lond. B. 1952. 327:37-72.
48. A. Madzvamuse. A Numerical approach to the study of spatial pattern forma-tion, D. Phil Thesis. Oxford University, UK, 2000: 1-150.
49. L. Wolpert. Cell Behaviour-Cartilage morphogenesis in the limb. Ed. Cambridge University, 1982: 1-100.
50. M. Dolnik, A. Zhabotinsky, A. B. Rovinsky, and I.R. Epstein. Spatio-temporal patterns in a reaction-diffusion system with wave instability. Chemical Engineering Science. 2000. 55:223-231.
51. R. Dillon, C. Gadgil, and H. Othmer. Short- and long-range effects of sonic hedgehog in limb development. PNAS. 2003. 100(18):10152-10157.
52. A. Madzvamuse, R. Thomas, P.K. Maini, and A. Wathen. A numerical approach to the study of spatial pattern formation in the ligaments of arcoidbivalves. Bulletin of Mathematical Biology. 2002. 64(3):501-530.
53. Herrero, M.A. The Mathematics of Chemotaxis. Handbook of Differential. Equations. Evolutionary Equations. Vol 3. Ed. Elsevier, 2007:1-100.
54. Ozgur B. Akan, Falko Dressler, Kenji Leibnitz, Taieb Znati. Special Issue on Bio-inspired computing and communication in wireless Ad Hoc and sensor networks Ad Hoc Networks. 2009. 7(4): 651-653.
55. Uichin Lee, Eugenio Magistretti, Mario Gerla, Paolo Bellavista, Pietro Lió, Kang on Lee. Bio-inspired multi-agent data harvesting in a proactive urban monitoring environment. Ad Hoc Networks. 2009. 7(4):725-741
56. Youshan Tao. Global existence of classical solutions to a combined chemotaxis-haptotaxis model with logistic source. Journal of Mathematical Analysis and applications. 2009. 354(1): 60-69.
57. Georgia Chalkiadaki, Dragana Nikitovic, Aikaterini Berdiaki, Maria Sifaki, Kostantinos Krasagakis, Pavlos Katonis, Nikos K. Karamanos, George N. Tzanakakis. Fibroblast growth factor-2 modulates melanoma adhesion and migration through a syndecan-4-dependent mechanism. The International Journal of Biochemistry & Cell Biology. 2009. 41(6):1323-1331.
58. A. Brovelli, F. Malaguerra, D.A. Barry Bioclogging in porous media: Model development and sensitivity to initial conditions. Environmental Modelling & Software. 2009. 24(5):611-626.
59. P. Namy, J. Ohayon, and P. Tracqui. Critical conditions for pattern formation and in vitro tubulogenesis driven by cellular traction fields. Journal of Theoretical Biology. 2004. 227(1):103-120.
60. G.F. Oster, J.D. Murray, and A.K. Harris. Mechanical aspects of mesenchymal Morphogenesis. J. Embryol. Exp. Morphol. 1983. 78:83-125.
61. A. Bru and M.A. Herrero. From The Physical Laws Of Tumor Growth To Modelling Cancer Processes. Mathematical Models and Methods in Applied Sciences, 2006. 7:1199-1218.
62. E.A. Reis, L.B.L. Santos, S.T.R. Pinho. A cellular automata model for avascular solid tumor growth under the effect of therapy. Physica A: Statistical Mechanics and its Applications. 2009. 388(7): 1303-1314.
63. D. R. Carter and M. Wong. The role of mechanical loading histories in the development of diarthrodial joints. J. Orthop Res. 1988. 6:804-816.
64. J.M. García-Aznar, J.H. Kuiper, M.J. Gómez-Benito, M. Doblaré, and J.B. Richardson. Computational simulation of fracture healing: Influence of interfragmentary movement on the callus growth. Journal of Biomechanics, 2007;40(7):1467-76.
65. D. R. Carter and GS Beaupr´e. Skeletal Function and Form - Mechanobiology of skeletal Development, Aging, and Regeneration. Ed. Cambridge University Press,N.Y., USA., 2001: 1-250.
66. S.J. Shefelbine. Mechanical Regulation of bone growth fronts and growth plates,PhD Thesis. Stanford University, 2002.
67. S. Shefelbine, C. Tardieu, and D. R. Carter. Development of the femoral bicondylar angle in hominid bipedalism. Bone. 2002. 30(5):765-770.
68. C.C. van Donkelaar and R. Huiskes. The PTHrP-Ihh feedback loop in the embryonic growth plate allows PTHrP to control hypertrophy and Ihh to regulate proliferation. Biomech Mod Mechanobiol. 2007. 6(1-2):55-62.
69. J.A. Izaguirre, R. Chaturvedi, C. Huang, T. Cickovski, J. Coffland, G. Thomas, Forgacs, M. Alber, G. Hentschel, S.A. Newman, , and J.A. Glazier. Compucell, a multi-model framework for simulation of morphogenesis. Bioinformatics. 2004. 20:1129-1137.
70. Centro de simulación de materiales y procesos. Disponible en: http://www.wag.caltech.edu/
71. Instituto Nacional de Imágenes biomédicas y bioingeniería. Disponible en: http://www.nibib.nih.gov/Research/MultiScaleModeling
72. Vlachos Research Group. En: http://www.dion.che.udel.edu/research.php

 

 

Aprobado:20 de junio de 2009.

 

 

Diego A. Garzón-Alvarado. Departamento de Ingeniería Mecánica y Mecatrónica. Facultad de Ingeniería. Universidad Nacional de Colombia.