TÉCNICA

 

 

El teorema de Bayes y su utilización en la interpretación de las pruebas diagnósticas en el laboratorio clínico

Bayes's theorem and its use in diagnostic test lectures in clinical laboratory

 

 

Dr. C. Raúl Fernández Regalado

Dpto de Bioquímica. Instituto de Ciencias Básicas y Preclínicas " Victoria de Girón". Universidad de Ciencias Médicas de La Habana. Cuba.

 

 

---

RESUMEN

La finalidad del laboratorio clínico es contribuir al diagnóstico médico confirmando o rechazando hipótesis por lo que se comprende la importancia de saber interpretar correctamente las pruebas diagnósticas. El resultado de una prueba diagnóstica puede permitir en primer lugar clasificar a un individuo como sano o enfermo. Además permite orientar su tratamiento, aportar información sobre su pronóstico o contribuir en la aplicación de medidas preventivas.

En el presente trabajo se propone y fundamente una nueva metodología, utilizando el teorema de Bayes, para decidir a partir de la prevalencia de la enfermedad y de los resultados de una prueba de laboratorio de la cual se conoce su sensibilidad y especificidad, cual es la probabilidad de que un paciente determinado tenga una enfermedad.

Este proceder pudiera ser introducido en la práctica, utilizando recursos informáticos sencillos, para las pruebas de laboratorio y también pudiera ser utilizado para pruebas diagnósticas de otras especialidades médicas.

 

Introducción

La finalidad del laboratorio clínico es contribuir al diagnóstico médico confirmando o rechazando hipótesis por lo que se comprende la importancia de saber interpretar correctamente las pruebas diagnósticas. El resultado de una prueba diagnóstica puede permitir en primer lugar clasificar a un individuo como sano o enfermo. Además permite orientar su tratamiento, aportar información sobre su pronóstico o contribuir en la aplicación de medidas preventivas.

Habitualmente para las pruebas diagnósticas en el laboratorio clínico se establece un intervalo de referencia previamente calculado Si los valores encontrados con una prueba diagnostica para algún paciente en particular se corresponden con los de un intervalo o rango obtenido en sujetos normales, el médico concluye : " los valores de este analito en este paciente son normales". Si por el contrario están fuera de ese intervalo, el medico concluye que al menos para ese analito aquel paciente no es normal e incluso pudiera llegar a clasificar al paciente como portador de determinada enfermedad.^1,2,3,4

En el presente trabajo se propone y fundamenta una nueva metodología, basada en el teorema de Bayes (5,6) para decidir a partir de la prevalencia de la enfermedad o una probabilidad a priori establecida y de los resultados de la prueba de laboratorio , cual es la probabilidad de que un paciente determinado tenga una enfermedad, lo cual contribuiría a identificar mejor a los pacientes con posibilidad de estar realmente enfermos.

 

Metodología

Thomas Bayes,⁵ un clérigo del siglo XVIII, desarrolló el siguiente teorema, que fue conocido después de su muerte, para el cálculo de probabilidades condicionales:

Sea { A1, A2, ….Ai….An} un conjunto de sucesos mutuamente excluyentes y cuya unión es el total o sea 1, y tales que la probabilidad de cada uno de ellos es distinta de cero. Sea B un suceso cualquiera del que se conocen las probabilidades condicionales P (B/Ai). Entonces la probabilidad P (Ai/B) viene dada por la expresión:

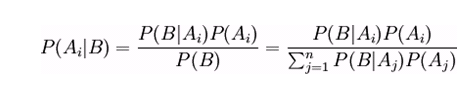
donde:

P(Ai) son las probabilidades a priori.
P(B / Ai) es la probabilidad de B en la hipótesis Ai.
P(Ai / B) son las probabilidades a posteriori.
Esto se cumple siempre que

Este teorema es válido en todas las aplicaciones de la teoría de la probabilidad aunque sin embargo, ha existido mucha controversia sobre el tipo de probabilidades que emplea. En esencia, los seguidores de la estadística tradicional también denominada objetivista o frecuencialista (6) sólo admiten probabilidades basadas en experimentos repetibles y que tengan una confirmación empírica mientras que los llamados estadísticos bayesianos permiten y defienden la la utilidad de las probabilidades subjetivas. El teorema, que ha resurgido con gran popularidad desde hace ya algunos años, puede servir entonces para indicar cómo debemos modificar nuestras probabilidades subjetivas cuando recibimos información adicional de un experimento. Este enfoque que propugna la estadística bayesiana está demostrando su utilidad en ciertas estimaciones basadas en el conocimiento subjetivo a priori y permitir revisar esas estimaciones en función de la evidencia , lo que está abriendo nuevas formas de hacer conocimiento.

Supóngase una prueba diagnóstica, por ejemplo nivel de glucosa en sangre, en ayunas, para diagnosticar la diabetes. Se considera que la prueba es positiva si se encuentra un nivel por encima de un cierto valor, digamos 120 mg/l.

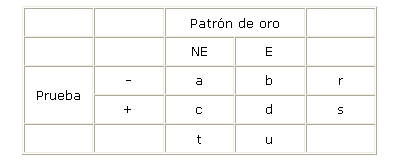
Para evaluar la prueba, para distintos puntos de corte, se somete a la misma a una serie de individuos diabéticos diagnosticados por otro procedimiento (el patrón de oro o "gold standar") y a una serie de individuos no diabéticos. Los resultados se pueden representar en una tabla de doble entrada.

Tabla. Resultado de la doble entrada

Si la prueba fuera perfecta b=c=0, desgraciadamente nunca ocurre. Se denomina falso-positivo (FP) al cociente c/t, y es una estimación de la probabilidad condicionada p(+|NE); se denomina falso-negativo (FN) al cociente b/u, y es una estimación de la probabilidad condicionada p(-|E). Estos dos valores cuantifican los dos errores que la prueba puede cometer y caracterizan a la misma. Simétricamente, los coeficientes que cuantifican los aciertos son la sensibilidad, p(+|E), y la especificidad p(-|NE).

Cuando la prueba se usa con fines diagnósticos (o de "screening") interesa calcular p(E|+) ( o valor Predicitivo Positivo VPP) y/o p(NE|-) ( o Valor Predicitivo Negativo VPN), que aplicando el teorema de Bayes y considerando los suceso Enfermedad (E) y No Enfermedad (NE) como una partición de A, tendremos la siguiente expresión:

Como E y NE son una partición, es decir sucesos incompatibles, usando el Teorema de Bayes

 

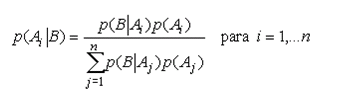
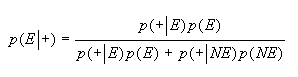
Pero de acuerdo a las definiciones hechas anteriormente es posible entonces expresar que:

y desde luego de manera similar se calcularía el VPN a partir de:

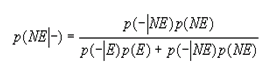
Que también se expresaría como:

Por ejemplo calculemos el VPP si se tratara de un paciente de 25 años, con dolor precordial, fumador y con una elevación en suero de una enzima útil en el diagnóstico de infarto del miocardio, suponiendo un 1 % de prevalencia para esta edad , y con un 90 % de sensibilidad y especificidad de la prueba un resultado positivo de la prueba se corresponde con un VPP de 8,3 %.

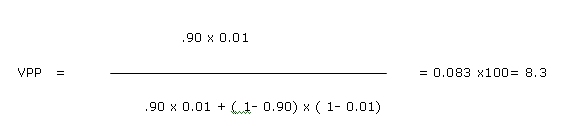
Sin embargo una prueba positiva en un paciente adulto de 68 años con dolor anginoso, fumador, dolor precordial y estimando un 90 % de prevalencia del infarto para este grupo poblacional , entonces el VPP será de 99 %. Es decir el paciente de 68 años y el joven de 25 tienen ambos positiva la misma prueba diagnóstica, sin embargo el de 68 años tiene una probabilidad mas de 10 veces mayor (99 vs. 8 %) de tener la enfermedad.

Considérese este otro ejemplo:

Se trata de una prueba de laboratorio que tiene un 95 % de sensibilidad y 95 % de especificidad. Pero conocemos a la vez que la prevalencia de la enfermedad en cuestión es de 5 por cada 1000 individuos en la población adulta. Haciendo uso de la fórmula (1) para calcular el Valor Predictivo Positivo ( VPP):

VPP= 0.95 X 0.005 / 0.95 X 0.005 + 0.05 X 0.995
= 0.00475/0.0545= 0.087

Lo cual significa que en 1000 test positivos que encontremos, sólo 87 corresponderán a enfermos y el resto serán individuos sanos.

Nótese que ambos Valores Predictivos ( VPP y VPN) dependen de la prevalencia de la enfermedad. Una prueba diagnóstica que funciona muy bien en la clínica Mayo de Estados Unidos , puede ser inútil en el Hospital Amejeiras de Cuba si la prevalencia de la enfermedad es distinta.

El VPP es un indicador útil pero no tanto para pacientes individuales. Un paciente llega a la consulta del médico con una determinada enfermedad que tiene una prevalencia o probabilidad de manifestarse en la población. Pero también llega con su historia personal, con variados antecedentes que predisponen o no a esa enfermedad. En un paciente individual , la " prevalencia" de la enfermedad puede orientar y ser considerada como la probabilidad a priori . También el médico, en base a un valor de prevalencia en la población en general pudiera asumir para aquel paciente un valor mayor o menor de probabilidad de contraer esa enfermedad, teniendo en cuenta su edad, antecedentes, factores genéticos , etc que conoce con precisión.. Desde luego, existe un componente subjetivo en todas estas estimaciones. Habitualmente los clínicos han expresado esta probabilidad a priori como " tengo la impresión de que este paciente tiene tal enfermedad ". Es cierto que existe un componente subjetivo en la asignación de una probabilidad a priori, pero nadie discute cuando un profesor dice de un alumno que conoce bien y sabe que no ha estudiado: " Estoy casi seguro que Pedro , que ha hecho tan mal curso, va a suspender" .

Por eso otro indicador útil puede ser el Odd o razón de probabilidades entre tener y no tener la enfermedad.

También utilizando el Teorema de Bayes es posible calcular los Odds finales a partir del conocimiento de la prevalencia de la enfermedad ( Odds iniciales) y de la calidad de la prueba diagnostica según la siguiente demostración sencilla:

ODDS ANTES= p(E)/p(NE)
ODDS DESPUES= p(E/+)/p (NE/ +)

 

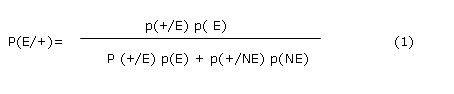
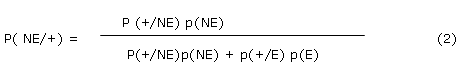
Dividiendo 1 entre 2

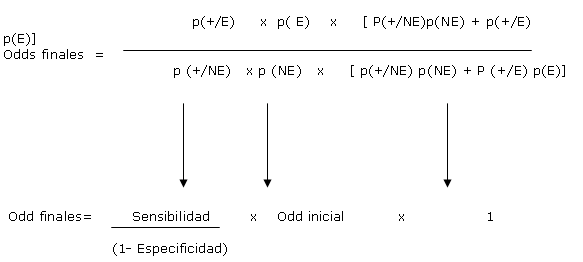
Al cociente Sensibilidad/( 1- Especificidad) se le conoce como razón de verosimilitud y para un punto de corte determinado para considerar la prueba positiva , tiene un valor que se relaciona con la calidad de la prueba

Según la anterior expresión conociendo o estimando la prevalencia inicial , o probabilidad previa asignada según la experiencia del médico y la información que posee acerca de la enfermedad en particular de su paciente , de otros estudios realizados, etc, es posible asignar un valor de odd inicial, y conociendo entonces la razón de verosimilitud ( o sea el cociente sensibilidad/1-especificidad) cuando la prueba da positiva para un punto determinado, es factible entonces calcular entonces los odd finales .

Vease el siguiente ejemplo:

1. Calcular los odds de que una hepatitis esté presente antes de realizar la ALAT en suero. Suponiendo que existe una probabilidad estimada de 12 % para esta enfermedad en determinada población y esa probabilidad es a la vez la probabilidad a priori para un determinado paciente que llega a la consulta médica. Entonces la probabilidad de no hepatitis será de ( 1-0.12)=0.88. Los odds serán entonces 0.12/0.88=0.14.
2. Calcular la razón de verosimiltud de la nueva información de la prueba diagnóstica , en este caso una determinación positiva en un paciente de Alanina Amino Transferasa (ALAT) (para la nueva información se reporta un 95 % de sensibilidad y un 90 % de especificidad). La razón de verosimilitud es 0.95/ 0.10= 9.5
3. Calcular los odds después de incorporar nueva información. ( El producto de los pasos 1 y 2. que es 0.14 x 9.5 = 1.33
4. Convertir los odds en probabilidad (Probabilidad= odds/ 1 + odds).
   Probabilidad= 1.33/2.33= 0.57

La ventaja del análisis Bayesiano al interpretar una prueba diagnóstica, puede consistir en que el clínico lograría una estimación mejor del riesgo que tiene un paciente de tener o contraer una enfermedad cuando la prueba le da positiva y no " andaría tan a ciegas" cuando el resultado de un análisis le llega a sus manos. .

En lugar del cálculo anterior son útiles los nomogramas, como el que se muestra a continuación, que están disponibles en algunos sitios de Internet.

La línea de la izquierda representa diversos valores de probabilidad previa a la prueba, la línea del medio corresponde a las diferentes RP (positivas o negativas) que podrían encontrarse en una prueba, y la línea de la derecha muestra las probabilidades de tener la enfermedad después del uso de la prueba. El procedimiento consiste sencillamente en trazar una línea recta entre la probabilidad previa de cada caso y el RP ( o Razón de verosimilitud) de la prueba que se está utilizando, y la continuación de esa línea recta hacia la derecha se cruzará con el valor correspondiente de probabilidad de tener la enfermedad, después de realizada la prueba diagnóstica. En este nomograma se puede apreciar, igualmente, que los cambios más significativos en la probabilidad de la enfermedad ocurren con pruebas que tienen RP mayores de 10 o menores de 0.1. Las pruebas con RP+ mayor de 10 y las pruebas con RP- menor de 0.1 usualmente son muy útiles para confirmar o descartar, respectivamente, una enfermedad.

Una alternativa al uso de estos nomogramas sería desarrollar un programa de computación sencillo para el cálculo de los odds finales y las probabilidades.

Este tipo de enfoque basado como se ha explicado en el enfoque estadístico bayesiano pudiera ser útil tambíén en otras especialices médicas, no relacionadas con el laboratorio clínico._7,8

 

CONCLUSIONES

1.- Se propone una metodología basada en el enfoque estadístico bayesiano para estimar la probabilidad de enfermedad en un paciente determinado con una prueba diagnostica de laboratorio positiva, y a partir también del conocimiento de la prevalencia de la enfermedad, o asignando una probabilidad a priori para un determinado paciente.

 

REFERENCIAS BIBLIOGRÁFICAS

1. Fescina RH, Simini F, Belitzky R. Evaluación de los procedimientos diagnósticos. Aspectos metodológicos. Salud Perinatal PP 1985; 2: 39-43.

2. Silva LC. Métodos estadísticos para la investigación epidemiológica. Seminario internacional de estadísticas en Euskadi. Instituto Vasco de Estadística; 1987.

3. Kassirer JP. Diagnostic Reasoning. Ann Intern Med 1989; 110: 893-5.

4. Fabián Jaimes. Pruebas diagnósticas: uso e interpretación Diagnostic tests: use and interpretation Acta Med Colomb vol.32 no.1 Bogotá Jan./Mar. 2007

5. Bacallao Jorge. Aspectos conceptuales y metodológicos en la investigación educacional. Universidad Mayor de San Andrés. Ed Buddy Lazo de la Vega. Biblioteca de Medcina Vol XVIII.La Paz, Bolivoia 1997.

6. Silva LC, Benavides A. El enfoque bayesiano: otra manera de inferir. Gac Sanit 2001; 15: 341 6.

7. Silva LC. Métodos estadísticos para la investigación epidemiológica. Seminario internacional de estadísticas en Euskadi. Instituto Vasco de Estadística; 1987.

8. D.E. Shapiro The interpretation of diagnostic tests. New England J. Medicine Stat Methods Med Res, June 1, 1999; 8(2): 113-34

 

 

Aprobado: 20 de junio de 2009

 

 

Dr. C. Raúl Fernández Regalado. Instituto de Ciencias Básicas y Preclínicas " Victoria de Girón". Universidad de Ciencias Médicas de La Habana. Cuba. Calle 146 No 3102, Cubanacán , Playa, Ciudad Habana. E mail: [e-mail]