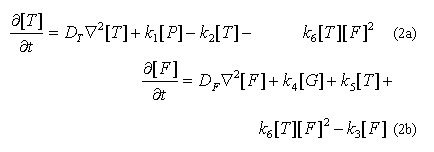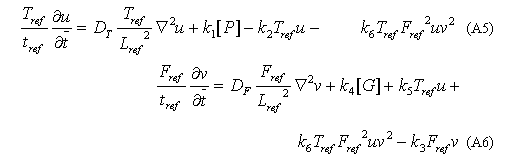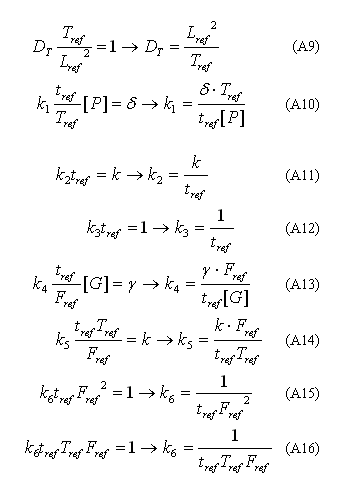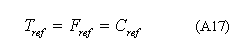ARTÍCULO ESPECIAL

 

Modelo matemático de la coagulación en la interfase hueso implante dental

Mathematical model of the bone-dental implant interface coagulation

 

Juan Carlos Vanegas A.^I; Nancy S. Landinez P.^I; Diego A. Garzón-Alvarado^II

^IMaestría en Ingeniería Biomédica. Grupo de Modelado Matemático y Métodos Numéricos (GNUM). Universidad Nacional de Colombia. Bogotá, Colombia.
^II Profesor Departamento de Ingeniería Mecánica y Mecatrónica. Grupo de Modelado Matemático y Métodos Numéricos (GNUM). Universidad Nacional de Colombia. Bogotá, Colombia.

 

---

RESUMEN

La recuperación de los tejidos lesionados tras la inserción de un implante dental inicia con la formación de un coágulo de fibrina que detiene el flujo de sangre y actúa como soporte inicial para las células osteoprogenitoras. La adecuada formación de este coágulo determina la conexión directa y estable entre el hueso y el implante, proceso conocido como oseointegración. El objetivo del presente trabajo es presentar un modelo matemático de la coagulación en la interfase hueso-implante dental basado en dos ecuaciones de reacción-difusión que representan la reacción cinética encargada de producir la fibrina y una ecuación de transformación que representa la formación de la red de fibras que compone el coágulo. Adicionalmente se incluye un parámetro asociado a la concentración de plaquetas en sangre que permite extender el alcance del modelo al análisis de dos desórdenes hematológicos conocidos: trombocitosis y trombocitopenia. La solución del modelo se realiza mediante el método de los elementos finitos obteniendo como resultado la distribución de patrones espacio-temporales en una sección de la interfase hueso-implante dental. Estos resultados concuerdan cualitativamente con resultados experimentales previamente reportados por otros autores. Aunque el modelo es versión simplificada del proceso biológico de la coagulación, los resultados obtenidos justifican la formulación matemática implementada. Se concluye que el modelo puede ser usado como base metodológica para la formulación de un modelo general de la oseointegración en la interfase hueso-implante dental.

Palabras Clave: Coagulación de la sangre, fibrina, interfase hueso-implante dental, modelo matemático.

---

ABSTRACT

The recovery of the injured tissues after the insertion of a dental implant begins with the formation of a fibrin clot that detains the blood flow and brings initial support for the osteoprogenitor cells. The adequate formation of this clot determines the direct and stable connection between bone and implant, process known as osseointegration. The aim of this work is to introduce a mathematical model of the coagulation in the bone-dental implant interface based on two reaction-diffusion equations representing the kinetic reaction that leads to the production of fibrin and a transformation equation representing the formation of the fibers network compounding the clot. The model also includes a parameter associated to the blood platelets concentration extending the model framework to the analysis of two hematological disorders well reported: thrombocytosis and thrombocytopenia. The solution of the model is performed using the finite element method, obtaining as results the distribution of spatial-temporal patterns in the bone-dental implant interface. These results are in qualitative concordance with experimental results previously reported by other authors. Although the model is a simplify version of the biological process of coagulation, the obtained results justify the mathematical formulation implemented. It is concluded that the model can be used as a methodological support in the formulation of a general model of the osseointegration in the bone-dental implant interface.

Key words: Blood clotting, fibrin, bone-dental implant interface, mathematical model.

---

 

 

INTRODUCCIÓN

Un implante dental es una pieza de biomaterial que se inserta en el hueso de la mandíbula para reemplazar la raíz de un diente y que alcanza una conexión firme, estable y duradera con el hueso que lo rodea, proceso conocido como oseointegración.^1,2 Una adecuada oseointegración está sujeta a la aceptación del implante por parte del tejido vivo así como a la formación de hueso funcional alrededor del implante (figura 1). Esta conexión o interfase hueso-implante depende de factores biológicos y sistémicos del paciente,^1,2,3 del diseño del implante,^4,5 de la distribución de carga entre el hueso e implante^5,6 y del procedimiento quirúrgico utilizado para la colocación del implante.^7,8

Figura 1. Microscopía electrónica de la interfase hueso-implante dental. Se observa la adaptación del hueso al perfil acanalado del implante (retirado durante la preparación de la muestra). Cortesía Facultad de Odontología, Universidad Nacional de Colombia sede Bogotá.

Con la oseointegración finaliza una serie de procesos biológicos de recuperación tisular iniciados con la lesión causada durante el procedimiento quirúrgico de inserción del implante. Esta lesión está condicionada al tipo de protocolo de inserción utilizado que típicamente consta de cuatro etapas [8]. En la primera, se retira la encía que cubre el hueso mandibular de la zona donde se ha de colocar el implante. En la segunda, se perfora el sitio de inserción en el hueso expuesto. En la tercera se inserta el implante en el hueso y en la cuarta se permite una recuperación inicial tanto del hueso como de los demás tejidos lesionados.^7,8

Aunque se utilizan técnicas que buscan minimizar el área de la lesión y que garantizan la viabilidad del tejido circundante al sitio de inserción, la presencia de sangrado es inevitable durante el procedimiento quirúrgico. El sangrado es la respuesta biológica inicial a la lesión y concluye con la formación del un tapón o coágulo que detiene el flujo de sangre. La posterior degradación de este coágulo permite la recuperación de las estructuras vasculares y la formación de una nueva red fibrilar de tejido conectivo primario denominado tejido granular sobre la que se deposita una nueva matriz extracelular que con el tiempo adquiere la estructura funcional del nuevo hueso y que permite la oseointegración del implante dental.^9,10 De esta manera, la formación del coágulo corresponde no sólo al bloqueo de la pérdida de sangre a causa de la lesión sino a la formación de la estructura sobre la cual se inician los procesos de recuperación tisular que culminan con la recuperación ósea.¹¹

Aunque gran parte del conocimiento relacionado con el proceso de coagulación proviene de modelos experimentales,¹² los modelos matemáticos y las simulaciones computacionales proporcionan información adicional sobre la interacción proteica, celular y tisular que tiene lugar.^13,14 En general, los modelos matemáticos de coagulación son de tres tipos: los modelos celulares, los modelos bioquímicos y los modelos de tiempo de coagulación.^13,15,16 Los modelos celulares describen la actividad celular asociada a la coagulación y la relación que existe entre la señalización bioquímica y los receptores del citoplasma celular.^13,17 En estos modelos el objetivo es obtener información sobre las concentraciones celulares que participan en la coagulación, y su influencia en la adecuada formación del coágulo respecto a las superficies celulares y extracelulares de contacto.¹⁵ Los modelos bioquímicos se basan en la descripción de la compleja cadena de señales bioquímicas que conducen a la formación de la fibrina y el coágulo. Aunque estos modelos son soportados por evidencia experimental de la vía de coagulación, no permiten obtener información adicional sobre condiciones patológicas, la mayoría de las veces asociadas a desordenes de la actividad de celula.^16,18 A partir de esta desventaja surgen los modelos de tiempo de coagulación, en los que como su nombre lo indica se analiza el tiempo que tarda la formación del coágulo y el equilibrio que debe existir entre células y proteínas procoagulantes.¹⁴ En particular, este tipo de modelos permite obtener información relacionada con la formación, crecimiento y posterior degradación del coágulo bajo situaciones hemostáticas normales así como en casos de desórdenes hemostáticos.^13,14,19

Aunque el interés de estos modelos es incuestionable, en la mayoría de ellos el problema de la coagulación es tratado como un fenómeno biológico que es necesario simplificar dada la compleja cadena de eventos bioquímicos asociada. Por esta razón, los resultados reportados por estos trabajos corresponden a curvas de evolución de concentraciones celulares y moleculares que controlan el proceso de coagulación con el objeto de hallar valores nominales apropiados para estas concentracione.^14,17 Adicionalmente, estos modelos carecen de una aplicación específica y por lo tanto no pueden ser utilizados directamente como herramienta de diagnóstico en un caso médico concreto.

El objetivo del presente trabajo es presentar un modelo matemático de la coagulación que adopta características de cada uno de los tres grupos de modelos mencionados y que además trata el problema de la coagulación en una aplicación específica, en este caso, la interfase hueso-implante dental. A diferencia de otros modelos,^16,20 nuestro enfoque de la coagulación se centra en las reacciones cinéticas de la vía común de la coagulación y en la influencia de las plaquetas y del tiempo de coagulación en la consolidación de la cicatrización inicial de la interfase hueso-implante dental. Con la solución del modelo en esta interfase se busca que los resultados sean aplicables a un caso médico concreto, en este caso, la formación de la red de fibrina que permite la adecuada oseointegración del implante dental. Para validar el modelo se siguieron dos estrategias. En primer lugar se realizaron simulaciones computaciones utilizando el método de los elementos finitos de las que se obtuvieron resultados que concuerdan cualitativamente con resultados experimentales, a nivel tanto espacial como temporal. Adicionalmente se realizaron dos modificaciones al modelo para evaluar su comportamiento ante condiciones patológicas específicas, de las cuales de nuevo se obtuvieron resultados que concuerdan con el caso experimental. En la siguiente sección se describe el proceso biológico de la coagulación y el modelo matemático propuesto. Luego se realiza la descripción de la simulación, los casos analizados y los resultados obtenidos. Finalmente se presenta la discusión de las limitaciones del modelo y las aplicaciones futuras.

 

MATERIALES Y MÉTODOS

Proceso biológico de la coagulación:

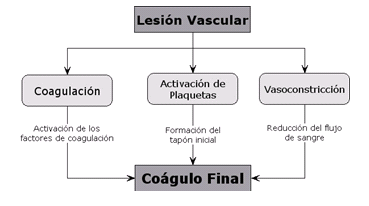
La coagulación es un proceso que hace parte del mecanismo de hemostasis encargado de proteger la integridad del sistema vascular luego de una lesión.²¹ En general, la recuperación vascular consta de tres etapas. Cuando un capilar es lesionado, la sangre entra en contacto con el tejido subendotelial rico en colágeno.²² Esto activa la cadena bioquímica de moléculas presentes en el plasma sanguíneo conocidas como factores de coagulación que concluye con la coagulación de la sangre.^12,22 Al mismo tiempo, las plaquetas transportadas por la sangre infiltrada se agrupan y forman un tapón inicial y el capilar lesionado se contrae (figura 2).^21,22 La acción conjunta de estos procesos crea el tapón final que detiene la pérdida de sangre y recupera la integridad del sistema vascular en la zona de la lesión.^11,21

Figura 2. La respuesta biológica ante una lesión vascular que termina con la formación del coágulo final comprende tres etapas simultáneas, a saber: 1) Coagulación y activación de los factores de coagulación, 2) Activación de las plaquetas y formación del tapón inicial, y 3) Vasoconstricción que causa la disminución de la pérdida de sangre.

El sangrado contiene glóbulos rojos, leucocitos y plaquetas.¹⁰ Aunque los glóbulos rojos están más orientados al transporte de oxígeno, son los leucocitos y las plaquetas las encargadas de iniciar el proceso de cicatrización.^10,11 Los leucocitos o glóbulos blancos son los encargados de iniciar la respuesta inmunológica, mientras que las plaquetas se encargan de detener el flujo de sangre al liberar una serie de gránulos.²¹ Estos gránulos contienen varias moléculas que gobiernan la actividad inicial en la zona de la lesión entre las que se destaca el fibrinógeno, una proteína que también está presente en el plasma sanguíneo.^22,23

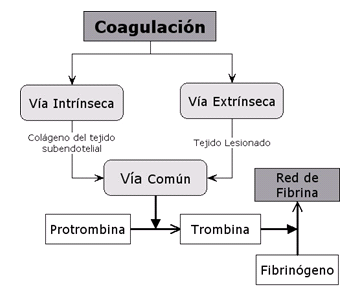
La cadena de reacciones que permite la coagulación de la sangre es aún motivo de estudio.²⁰ Sin embargo, se han logrado determinar dos vías que conducen a la formación del coágulo. La primera es la vía intrínseca, activada cuando la sangre transportada por el sistema vascular entra en contacto con otras superficies como el ambiente subendotelial rico en colágeno o algunas superficies negativamente cargadas como el vidrio.^20,22 La segunda vía de coagulación o vía extrínseca es activada por la presencia de una lesión vascular que induce una respuesta bioquímica desde los tejidos dañados.^11,22 Se ha determinado que estas dos vías se combinan en una vía común que conduce a la producción de trombina a partir de su precursor, la protrombina.^21,24 La protrombina es una proteína presente en el plasma sanguíneo que es transformada en trombina por acción de los factores de coagulación. La función de la trombina es convertir el fibrinógeno presente en la sangre infiltrada en monómeros de una nueva proteína denominada fibrina (figura 3). Los monómeros de fibrina se agregan en fibras entrecruzadas que crean una red tridimensional que detiene completamente el flujo de sangre y que además protege los tejidos dejados al descubierto tras la inserción del implante.¹¹ Esta red de fibras conforma el denominado coágulo de fibrina o coágulo final.^22,23

Figura 3. La coagulación puede activarse por acción del tejido subendotelial (vía intrínseca) o por acción del tejido lesionado (vía extrínseca). Ambos tipos de activación conducen a una vía común en la que la protrombina es convertida en trombina, que a su vez convierte el fibrinógeno presente en la sangre infiltrada en la red de fibrina que compone el coágulo final.

Modelo Matemático:

Aunque el proceso de coagulación comprende una compleja cadena de eventos celulares y moleculares, la formación del coágulo de fibrina puede verse fundamentalmente como la conversión de trombina en fibrina.²² Ya que ambas sustancias se encuentran en la sangre, puede suponerse que la conversión se inicia una vez que se detiene el flujo de sangre en la zona de la lesión, es decir, después de la activación y agregación de las plaquetas y una vez que los factores de coagulación activan la vía común (figura 2).^21,22 Un mecanismo de conversión de este tipo puede entenderse como una reacción cinética entre dos sustancias, a saber, trombina y fibrinógeno, donde la primera sustancia es el agente activador y la segunda sustancia el agente de conversión.^25,26 Este tipo de reacción cinética se expresa utilizando la Ley de acción de masas de la siguiente manera:²⁷

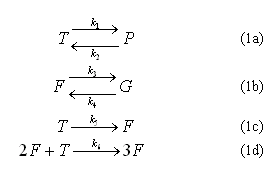
En (1), T es la concentración de trombina, F es la concentración de fibrinógeno, P es la concentración de protrombina y G es la concentración de gránulos liberados por las plaquetas. De acuerdo a la Ley de acción de masas, al duplicar la concentración de una de las sustancias de entrada se duplica la tasa de colisión entre las moléculas, lo que a su vez aumenta al doble la concentración de los productos de la reacción.²⁷ De (1) se observa que la trombina se forma a partir de la protrombina, mientras que el fibrinógeno se considera como un subproducto de los gránulos liberados por las plaquetas.²⁸ La ecuación (1a) establece que la protrombina es el precursor de la trombina, la ecuación (1b) indica que el fibrinógeno proviene de los gránulos liberados por las plaquetas, y las ecuaciones (1c) y (1d) establecen que la trombina inicia el proceso de formación de fibrinógeno. A partir de (1) se obtiene el siguiente sistema de ecuaciones diferenciales:

En (2) las ecuaciones dadas en (1) son complementadas con un término de transporte que tiene en cuenta la difusión tanto de trombina como de fibrinógeno. De esta manera, es posible analizar el cambio en la concentración de estas sustancias en el tiempo como un proceso difusivo que depende de los términos de formación y degradación contenidos en la ley de acción de masas. La reacción cinética dada en (2) es complementada con una tercera expresión que describe explícitamente la formación de fibrina y que está dada por la siguiente ecuación:

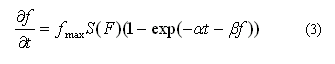
En (3) f es la concentración de fibrina, fmax es el valor máximo de la concentración de fibrina,²⁹ es la tasa de activación de fibrina relacionada con la tasa de polimerización de las fibras de fibrina²³ y es el factor de calidad de sangre que relaciona la conversión de fibrinógeno en fibrina con el número de plaquetas.³⁰ Este parámetro permite ampliar el rango de aplicaciones del modelo (apéndice A, B y C). La función S(v) se encarga de transmitir el patrón de conversión iniciado en (2) y corresponde a una función de activación escalón dada por la expresión:

donde w es el valor umbral de polimerización y p es una constante que ajusta la pendiente de la activación.

A partir de un análisis numérico dimensional, del análisis de la literatura disponible y utilizando los resultados reportados para el modelo de glucólisis que genera patrones espacio-temporales similares a los buscados,²⁵ se obtienen los valores de los parámetros del modelo descrito por las ecuaciones (2) y (3). La tabla 1 resume estos valores. Una revisión detallada de su origen puede encontrarse en el apéndice A.

Descripción de la simulación:

El modelo propuesto se implementó numéricamente mediante el método de los elementos finitos usando como dominio una malla bidimensional de elementos lineales que reproduce una sección de la interfase entre el borde del hueso y el perfil acanalado de un implante dental (figura 4). La geometría y dimensiones del perfil del implante se obtuvieron a partir de información proporcionada por el fabricante de implantes dentales MIS Technologies Ltd. (Shlomi, Israel). El ancho de la interfase corresponde a observaciones experimentales del espesor de la capa de proteínas que se adhiere a la superficie del implante y del volumen de tejido necrótico causado por el procedimiento de inserción.^35,36

Figura 4. a) Esquema del sitio de inserción de un implante dental. b) Geometría de la interfase formada entre el hueso y el implante. c) Diagrama y dimensiones de la sección de interfase usada como dominio bidimensional.

La malla finalmente utilizada consta de 18.728 elementos cuadriláteros bilineales de cuatro nodos para un total de 18.417 nodos. Las condiciones iniciales para las ecuaciones de trombina y fibrinógeno corresponden a pequeñas perturbaciones del estado estable obtenido mediante el análisis matemático de las ecuaciones de reacción-difusión y el denominado espacio de Turing.²⁶ Como la fibrina es un producto de la reacción cinética entre la trombina y el fibrinógeno, la condición inicial para la ecuación (3) se supone igual a cero. En todos los casos se asumen condiciones de flujo en el contorno iguales a cero, lo que supone la formación de un tapón inicial de plaquetas que detiene el flujo de sangre en la zona de la lesión. El tiempo de simulación corresponde al tiempo necesario para la formación de la fibrina y del coágulo final y se asume igual a diez minutos.³⁷ La solución computacional se obtuvo usando un computador portátil con procesador AMD Turion 64X2 1.6GHz, 2GB RAM en un tiempo total de cuatro y media horas.

Casos Analizados:

Como se describió en la introducción, las plaquetas hacen parte del proceso de formación del coágulo final. En condiciones normales, una persona tiene entre 150x10⁹ y 400x10⁹ plaquetas por litro de sangre.³⁸ Sin embargo, desordenes del mecanismo de producción de las plaquetas alteran el nivel normal de concentración de estas células y causan anormalidades en el mecanismo de coagulación.24 El aumento en el nivel de plaquetas (600x109 - 700x109 células por litro) causa trombocitosis, un desorden de la sangre que usualmente es asintomático pero que aumenta el riesgo de formación de trombos, infartos cardíacos e isquemia localizada.³⁹ En casos de trombocitosis extrema el número de plaquetas puede ser incluso mayor a 1.000x10⁹ células por litro.⁴⁰ Por el contrario, la disminución en el nivel de plaquetas (menos de 150x109 células por litro) o trombocitopenia es un desorden caracterizado por la inadecuada formación del coágulo y el aumento en el riesgo de sangrado,³⁹ que puede ser espontáneo si el número de plaquetas es menor a 20x109 células por litro.^24,31

Para la evaluación del modelo matemático propuesto se toma como ejemplo una condición clínica en la que el conteo de plaquetas es normal y se simula la formación de la red de fibrina. Los parámetros usados son explicados en detalle en el apéndice A. Adicionalmente se toman por separado una condición de trombocitosis y una de trombocitopenia. En los dos casos de simuló la formación de la red de fibrina. En todos los casos se mantuvieron las condiciones iniciales y de contorno ya mencionadas. Los cambios en los parámetros para las simulaciones de trombocitosis y trombocitopenia se explican en detalle en los apéndices B y C respectivamente.

 

RESULTADOS

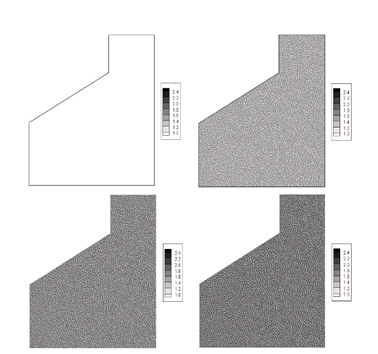
El modelo que aquí se presenta simula la formación del coágulo de sangre en la interfase hueso-implante dental a partir de la reacción cinética entre la trombina y el fibrinógeno. Esta reacción está caracterizada por la formación de patrones espacio-temporales que suponen la formación de la red de fibrina que compone el coágulo final (figura 5). A partir del estado inicial en el que no existe fibrina (figura 5a), el modelo predice la aparición del patrón espacio-temporal en 2 minutos (figura 5b), 5 minutos (figura 5c) y 10 minutos (figura 5d). Como el tiempo necesario para la formación del coágulo de fibrina es de 10 minutos,^11,37 se supone este tiempo como el tiempo en el que el patrón alcanza su estado estable. En ningún caso el patrón espacio-temporal toma valores de concentración superiores a 2.5 mg/ml, que corresponde al valor máximo dado por la concentración típica de fibrina que se reporta en.²⁹

Figura 5. Evolución temporal de la formación de fibrina en el dominio bidimensional (en mg/ml) a) Condición inicial, b) 2 minutos,
c) 5 minutos, d) 10 minutos.

Para observar la evolución temporal de la formación fibrilar, se seleccionó un punto cerca del centro del dominio y se extrajeron los valores de trombina, fibrinógeno y fibrina. Las figuras 6,7,8 resumen los valores obtenidos, de las cuales puede verse que mientras la concentración de trombina disminuye en el tiempo, la concentración de fibrinógeno aumenta hacia su estado estable. Este hecho pone en evidencia la reacción cinética de activación existente entre las dos sustancias, es decir, la concentración de trombina disminuye por el consumo que se requiere para la transformación del fibrinógeno en fibrina mientras la activación de plaquetas por la presencia de trombina aumenta la concentración de fibrinógeno.³⁰ Luego el fibrinógeno comienza su transformación en fibrina con lo cual la concentración de está última aumenta hasta alcanzar el valor de estado estable.23

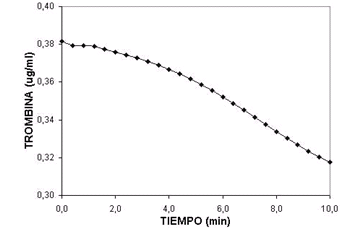
Figura 6. Evolución temporal de la trombina para un punto cercano al centro del dominio bidimensional.

 

Figura 7. Evolución temporal del fibrinógeno para un punto cercano al centro del dominio bidimensional.

 

Figura 8. Evolución temporal de la fibrina para un punto cercano al centro del dominio bidimensional.

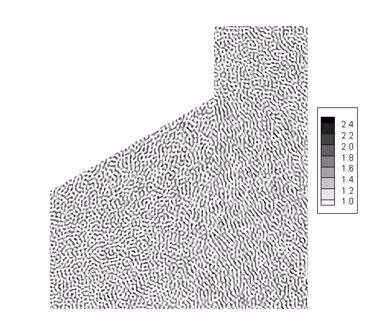
La característica espacial propia de esta reacción conduce a la formación de un patrón de fibras de fibrina. Haciendo un acercamiento mediante la reducción del dominio a un cuadrado de 1 m de lado y el escalamiento espacial del modelo, es posible apreciar en detalle la distribución fibrilar de la fibrina en estado estable (figura 9). Esta distribución está caracterizada por el agrupamiento de zonas de igual concentración de fibrina en arreglos similares a fibras entrelazadas que en ningún caso sobrepasan el valor de concentración máximo de fibrina, es decir, 2.5 mg/ml.²⁹

 

Figura 9. Detalle del estado estable de la formación de fibrina (en mg/ml).

Ya que la formación del patrón espacio-temporal está relacionada con la activación de plaquetas, la variación en la concentración de estas células conduce a variaciones en los niveles de fibrinógeno y éstas a su vez a variaciones en los niveles de fibrina. Debido a esto, el modelo puede extenderse al análisis de los dos desórdenes plaquetarios antes mencionados: trombocitosis y trombocitopenia. En la figura 10 se muestra el estado estable alcanzado por la fibrina cuando la concentración de plaquetas es 1.000x109 células por litro. Bajo estas condiciones, aunque la concentración de fibrina se mantiene dentro de su valor máximo, se observa que la densidad de la formación del patrón es mayor respecto al resultado de la figura 5d, donde la concentración de plaquetas usada es 300x10⁹ células por litro. En contraste, cuando la concentración de plaquetas disminuye a 20x109 células por litro, nivel característico de la trombocitopenia, se obtiene un patrón de fibrina cuyo estado estable tiene una densidad menor respecto de la figura 5d. Este resultado se muestra en la figura 11.

Figura 10. Estado estable de la fibrina cuando la concentración de plaquetas corresponde a trombocitosis (en mg/ml).

 

Figura 11. Estado estable de la fibrina cuando la concentración de plaquetas corresponde a trombocitopenia (en mg/ml).

Aunque cualitativamente se puede observar que en las figuras 5, 10 y 11 existen diferencias en la densidad del patrón espacio-temporal, una prueba sencilla permite cuantificar esta diferencia. Tomando los estados estables de fibrina en cada uno de los tres casos, es decir, nivel normal de plaquetas, trombocitosis y trombocitopenia, se realizó una ponderación en el dominio obteniendo el valor medio de la concentración de fibrina. En el caso del valor normal de plaquetas se obtuvo como valor medio una concentración de 1.7552 mg/ml. Por su parte, en trombocitosis se obtuvo una concentración de 1.9961 mg/ml, mientras que en trombocitopenia se obtuvo un valor de 1.2206 mg/ml. Comparando los resultado se observa cuantitativamente que el número de plaquetas modifica la concentración media de fibrina formada y en consecuencia, la calidad del coágulo final. Es decir, en el caso de trombocitosis la mayor densidad en el coágulo indica una mayor probabilidad de formación de fragmentos o trombos, mientras que en el caso de trombocitopenia una menor densidad del coágulo indica la mayor probabilidad de hemorragias y sangrado espontáneo, lo cual concuerda con lo que se reporta en la literatura medica.^24,40

Para la predicción de la formación de la red fibrilar, las suposiciones hechas a la cadena de la coagulación permiten obtener resultados que concuerdan con el caso experimental. Prueba de ello es la asimetría del patrón espacio-temporal obtenido y las dimensiones de las fibras de fibrina. Microfotografías tomadas a coágulos de sangre formados un día después de la fractura del fémur de una rata muestran la disposición que a manera de puntos alargados adquiere la red de fibrina⁴² de manera semejante al patrón mostrado en la figura 5. Adicionalmente, pruebas experimentales han establecido que las fibras de fibrina pueden tener entre 100 y 500 nm de ancho.^23,29,43 En la figura 9 se observa que el ancho de las fibras (gris oscuro) obtenido mediante la simulación es de aproximadamente 250 nm, valor que se ajusta al intervalo experimental mencionado.

 

DISCUSIÓN

El objetivo de este trabajo es presentar un modelo matemático de la coagulación en la interfase hueso-implante dental. El modelo está basado en dos suposiciones. En primer lugar se adopta un enfoque reducido del fenómeno de la coagulación en el cual la formación del coágulo de fibrina depende de la reacción cinética entre la trombina y el fibrinógeno. Este hecho permite simplificar el fenómeno de la coagulación al iniciarlo luego que los factores de coagulación activan la vía común y comienza la formación de la red de fibras de fibrina.^12,21,22 En la segunda suposición se han considerado el tiempo de coagulación y el número de plaquetas como indicadores del tipo de coágulo formado. Esta segunda hipótesis garantiza que el modelo no sólo tenga en cuenta la interacción bioquímica de las dos sustancias de interés sino también el tiempo de coagulación y la concentración de células sanguíneas, en este caso, las plaquetas.^14,17,18 Bajo estas suposiciones el modelo es capaz de predecir la formación de la red de fibras de fibrina en una sección de la interfase hueso-implante dental a partir de la aparición de patrones espacio-temporales distribuidos en el dominio analizado aplicando una restricción para la estabilidad en el tiempo³⁷ y una característica de formación dada por la concentración de plaquetas.^10,41

Se debe admitir que el modelo es sólo una aproximación a la realidad del fenómeno biológico de la coagulación, y por lo tanto, existen una serie de limitaciones asociadas al enfoque utilizado. La primera limitación consiste en la simplificación hecha a la cadena de eventos moleculares que rodean la coagulación. Como se describe en la figura 2, la formación de la red de fibrina es una consecuencia de la activación de la vía intrínseca y extrínseca que confluyen en la denominada vía común. En el modelo presentado, la vía común se supone iniciada y el desarrollo del coágulo se presente a partir de la conversión de fibrinógeno en fibrina. No obstante, la activación de las vías intrínseca y extrínseca supone a su vez la activación de una amplia cadena de moléculas que han sido estudiadas por múltiples trabajos experimentales y que en algunos casos siguen siendo motivo de investigación.²⁰

La segunda limitación está relacionada con la activación celular y molecular causada por la superficie del implante dental. Está ampliamente reportado que la superficie del implante dental estimula la activación de las plaquetas y el anclaje de las redes de fibrina que posteriormente proporcionan el soporte para la migración y diferenciación de las células osteoprogenitoras encargadas de la recuperación del hueso lesionado.^10,11 Aunque en el modelo propuesto no se tiene en cuenta este aspecto, se reconoce que la superficie del implante influye no sólo en la formación del coágulo de fibrina sino en la adecuada oseointegración del implante, razón por la cual, la extensión del modelo al caso general de recuperación ósea debe considerar la superficie bioactiva del implante.

La tercera limitación está relacionada con las condiciones iniciales y de contorno. Si bien las condiciones iniciales fueron obtenidas de las concentraciones promedio reportadas en la literatura, de la cadena de activación de los factores de coagulación durante las vías intrínsecas y extrínsecas dependen las concentraciones que finalmente se encuentran en la etapa de conversión de fibrinógeno a fibrina.^12,22,23 Estas variaciones afectan la formación de la red fibrilar, y por lo tanto, un análisis completo de la cadena de eventos moleculares previos a la conversión del fibrinógeno en fibrina permite ampliar la aplicación del modelo a desórdenes de la actividad molecular de algunos factores de coagulación, células y tejidos que alteran las concentraciones iniciales de trombina, fibrinógeno y fibrina.¹² En cuanto a las condiciones de contorno, asumir el flujo de sangre igual a cero en el tiempo cero supone la formación de un coágulo inicial que detiene la pérdida de sangre y confina la sangre infiltrada a la zona creada entre la superficie del implante y el borde del hueso circundante. Este coágulo inicial supone la activación de las plaquetas y la activación del proceso de vasoconstricción de los vasos sanguíneos averiados.²¹ Sin embargo, en el acercamiento realizado a través del modelo, la vasoconstricción, y en general, la recuperación de la red vascular no se tiene en cuenta ya que la cantidad de sangre infiltrada en la zona de la lesión no es un parámetro analizado, y además es suficiente con suponer una concentración promedio de plaquetas en sangre para referirse a su activación y agregación. Adicionalmente, la recuperación de la red vascular se considera igual a la formación de la red fibrilar, toda vez que la formación de fibrina se da a lo largo de los vasos sanguíneos recuperados.¹¹

En cuarto lugar, los parámetros del modelo fueron algunos estimados de la literatura disponible, otros fueron estimados a partir de resultados experimentales y otros fueron tomados directamente de trabajos numéricos previamente reportados. Sin embargo, el valor exacto de muchos de ellos es una incógnita, siendo necesario ajustarlos de manera que la formación de los patrones espacio-temporales fuera la esperada (Apéndice A). La dificultad para obtener los valores adecuados a partir de pruebas experimentales es una debilidad que comparte el modelo con otros trabajos en el área del modelado computacional de fenómenos biológicos. Sin embargo, se debe destacar que los valores hallados numéricamente se pueden correlacionar con otros encontrados en trabajos experimentales, lo cual hace que el modelo sea viable desde el punto de vista biológico.

A pesar de estas limitaciones, el modelo presentado puede considerarse como un avance en el modelado computacional de la coagulación, en especial por adoptar características de cada uno de los tres tipos de modelos tradicionalmente reportados. En particular, la posibilidad de predecir la formación del coágulo respecto a variaciones de la concentración de plaquetas es una forma sencilla de analizar desórdenes hematológicos, en especial cuando en la práctica médica el diagnóstico de estos desórdenes depende de pruebas de conteo celular.^40,41 Finalmente, la complejidad del fenómeno biológico obliga a realizar simplificaciones de manera que se pueda obtener un modelo viable para su solución computacional. No obstante las limitaciones, los resultados obtenidos muestran la capacidad del modelo presentado de reproducir características importantes del proceso biológico de la coagulación en implantes dentales que concuerdan con resultados experimentales.^10,19,42

La ampliación del modelo presentado con las etapas de recuperación tisular posteriores a la coagulación de la interfase hueso-implante dental debe permitir obtener resultados ajustados al proceso de oseointegración, toda vez que la formación de nuevo hueso depende en gran medida de una adecuada formación de la red de fibras de fibrina sobre la cual inicia la migración y diferenciación de células osteoprogenitoras.^10,11 El modelo presentado, en concordancia con la perspectiva biológica, contiene las bases para el modelado de las siguientes etapas de recuperación ósea y plantea la necesidad de tener en cuenta la superficie bioactiva del implante dental no sólo como agente modificador de la estructura tisular en la interfase hueso implante dental sino como una superficie que modifica las condiciones iniciales y de contorno del modelo.

 

AGRADECIMIENTOS

Los autores agradecen el apoyo y la información suministrada por MIS Technologies Ltda. y su oficina de representación en Colombia, especialmente a la Dra. Claudia Esparza y al Dr. Martín Casale. Este trabajo hace parte del proyecto de investigación 202010011460 financiado con recursos de la Universidad Nacional de Colombia.

 

REFERENCIAS BIBLIOGRÁFICAS

1. Schenk RK, Buser D. Osseointegration: a reality. Periodontology 2000 1998; 17: 22-35.

2. Albrektsson T, Johansson C. Osteoinduction, osteoconduction and osseointegration Eur. Spine J. 2001; 10: S96-S101.

3. Cooper L. Biological determinants of bone formation for osseointegration: Clues for future clinical improvements. J. Prosthet Dent. 1998; 80 [4]: 439-449.

4. Matsuno H, Yokoyama A, Watari F, Uo M, Kawasaki T. Biocompatibility and osteogenesis of refractory metal implants, titanium, hafnium, niobium, tantalum and rhenium. Biomaterials 2001; 22: 1253-1262.

5. Gapski R, Wang HL, Mascarenhas P, Lang N. Critical review of immediate implant loading. Clin. Oral Impl. Res. 2003; 14: 515-527.

6. Sikavitsas V, Temenoff J, Mikos A. Biomaterials and bone mechanotransduction. Biomaterials 2001; 22: 2581-2593.

7. Fragiskos FD, Alexandridis C. Osseointegrated Implants. En: Fragiskos FD, Alexandridis C. Oral Surgery. Springer Berlin Heidelberg; 2007.

8. Branemark PI. Osseointegration and its experimental background. J. Prosthet Dent. 1983; 50 [3]: 399-410.

9. Saffar JL, Lasfargues JJ, Cherruau M. Alveolar bone and the alveolar process: The socket that is never stable. Periodontology 2000 1997; 13: 76-90.

10. Davies J. Understanding peri-implant endosseous healing. Journal of dental education 2003; 67 (8): 932-949.

11. Aukhil I. Biology of wound healing. Periodontology 2000 2000; 22: 44-50.

12. Butenas S, Mann KG. Blood coagulation. Biochemistry 2002; 67 (1): 3-12.

13. Nielsen VG. Beyond cell based models of coagulation: Analyses of coagulation with clot lifespan resistance-time relationships. Thrombosis Research 200; 122: 145-152.

14. Khanin MA, Rakov DV, Kogan AE. Mathematical model for the blood coagulation prothrombin time test. Thrombosis Research 1998; 89: 227-232.

15. Colijn C, Mackey MC. A mathematical model of hematopoiesis I. Periodic chronic myelogenous leukaemia. Journal of Theoretical Biology 2005; 237: 117-132.

16. Zarnitsina VI, Pokhilko AV, Ataullakhanov, FI. A mathematical model for the spatio-temporal dynamics of intrinsic pathway of blood coagulation I. The model description. Thrombosis Research 1996; 84 (4): 225-236.

17. Santillan M, Mahaffy JM, Belair J, Mackey MC. Regulation of platelet production: the normal response to perturbation and cyclical platelet disease. Journal of Theoretical Biology 2000; 206: 585-603.

18. Hoffman M. A cell-based model of coagulation and the role of factor VIIa. Blood Reviews 2003; 17: S1-S5.

19. Caterina R De, Lanza M, Manca G, Strata GB, Maffei S, Salvatore L. Bleeding time and bleeding: an analysis of the relationship of the bleeding time test with parameters of surgical bleeding. Blood 1994; 84 (10): 3363-3370.

20. Cunha Orfao S, Janka G, Mottaghy K, Walcher S, Zerz E. Qualitative properties and stabilizability of a model for blood thrombin formation. J. Math. Anal. Appl. 2008; 346: 218-226.

21. Pasi KJ. Hemostasis. En: Perry DJ, Pasi KJ. Hemostasis and thrombosis protocols. Humana Press 1999. 3-24.

22. Minors DS. Haemostasis, blood platelets and coagulation. Anaesthesia and intensive care medicine 2007; 8 (5): 214-216.

23. Gorkun OV, Veklich YI, Weisel JW, Lord ST. The conversion of fibrinogen to fibrin: recombinant fibrinogen typifies plasma fibrinogen. Blood 1997; 89 (12): 4407-4414.

24 Shuey KM. Platelet-associated bleeding disorders. Seminars in oncology nursing 1996; 12 (1): 15-27.

25. Painter KJ. Chemotaxis as a mechanisms for morphogenesis [PhD Thesis]. United Kingdom: Oxfod University, 1997. 3-25.

26. Murray JD. Mathematical Biology I. An introduction. Springer-Verlag, 2001. 405-509.

27. Garzón-Alvarado DA. Simulación de procesos de reacción difusión: aplicación a la morfogénesis del tejido óseo. [Tesis de Doctorado]. Zaragoza, España: Centro Politécnico Superior de la Universidad de Zaragoza. 2007. pp. 38-70.

28. Handagama P, Scarborough RM, Shuman MA, Bainton DF. Endocytosis of fibrinogen into megakaryocyte and platelet a-granules is mediated by IIb 3 (glycoprotein IIb-IIIa). Blood 1993; 82 (1): 135-138.

29. Wiesel JW. The mechanical properties of fibrin for basic scientists and clinicians. Biophysical Chemistry 2004; 112: 267-276.

30. Schulz-Heik K, Ramachandran J, Bluestein D, Jesty J. The extent of platelet activation under shear depends on platelet count: differential expression of anionic phospholipid and Factor Va. Pathophysiol Haemost Thromb 2005; 34:255-262.

31. Harmison CR, Lakdaburu Ch, Seeger WH. Some physicochemical properties of bovine thrombin. Journal of Biological Chemistry 1961; 236 (6): 1693-1696.

32. Hall CE, Slayter HS. The fibrinogen molecule: its size, shape, and mode of polymerization. J. Biophysic. And Biochem. Cytol. 1959; 5 (1): 11-17.

33. López JA, Del Conde I, Dong JF. Platelet function under flow. En: Quinn M, Fitzgerald D. Platelet Function: assessment, diagnosis and treatment. Humana Press 2005. 223-246.

34. Hantgan RR, Hermans J. Assembly of fibrin: a light scattering study. Journal of Biological Chemistry 1979; 254 (22): 11272-11281.

35. Kasemo B, Lausmaa J. The biomaterial-tissue interface and its analogues in surface science and technology. En: Davies JE. The bone-biomaterial interface. University of Toronto Press, 1991. 19-32.

36. Ellingsen J, Thomsen P, Lyngstadaas P. Advances in dental implant materials and tissue regeneration. Periodontology 2000 2006; 41: 136-156.

37. Malmquist JP, Clemens SC, Oien HJ, Wilson SL. Hemostasis of oral surgery wounds with the HemCon dental dressing. J. Oral Maxillofac. Surg. 2008; 66:1177-1183.

38. Kaushansky K. The molecular mechanisms that control thrombopoiesis. J. Clin. Invest. 2005; 115:3339-3347.

39. Patel SR, Hartwig JH, Italiano Jr JE. The biogenesis of platelets from megakaryocyte proplatelets. J. Clin. Invest. 2005; 115:3348-3354.

40. Teffery A. Thrombocytosis and essential thrombocytopenia. En: Michelson AD. Platelets. Elsevier, 2007. 1009- 1028.

41. Mannucci PM. Few platelets, many platelets: the role of the internist. European Journal of Internal Medicine 2000; 11: 4-8.

42. Davies JE, Hosseini MH. Histodynamics of endosseous wound healing. En: Davies JE. Bone Engineering. Em square incorporated, Toronto, 2000. 1-14.

43. Wolberg AS, Campbell RA. Thrombin generation , fibrin clot formation and hemostasis. Transfusion and Apheresis Science 2008; 38: 15-23.

44. Bailon-Plaza A, van der Meulen MCH. A mathematical framework to study the effects of growth factor influences on fracture healing. Journal of Theoretical Biology 2001; 212: 191-209.

45. Brennan MT, Shariff G,Louise MK, Fox PC, Lockhart PB. Relationship between bleeding time test and postextraction bleeding in a healthy control population. Oral Surg Oral Med Oral Pathol Oral Radiol Endod 2002; 94: 439-43.

46. Mann KG. Thrombin formation. Chest 2003; 124: 4-10.

47. Bouchard BA, Butenas S, Mann KG, Tracy PB. Interactions between platelets and the coagulation system. En: Michelson AD. Platelets. Elsevier, 2007. 377-402.

APÉNDICE A

Las ecuaciones (2a) y (2b) fueron adimensionalizadas utilizando las siguientes escalas [44]:

En las expresiones (A1) a (A4), u, v, y corresponden a los valores adimensionales de trombina, fibrinógeno, tiempo y espacio respectivamente.

Utilizando estas escalas y reemplazando en las ecuaciones (2a ) y (2b) se obtiene:

Multiplicando (A5) por t_ref / T_ref (A6) y por t_ref / F_ref y omitiendo la notación de barra de los valores adimensionales se tiene:

En (A7) y (A8) se eligen las siguientes constantes:

La constante DT de la ecuación (A9) corresponde a constante de difusión de la trombina calculada a partir del tiempo y la longitud de referencia. Por su parte, la constante k₁ es la tasa de conversión de la protrombina en trombina, k₂ es la tasa de consumo de trombina, k₃ es la tasa de consumo de fibrinógeno en presencia de trombina, k₄ es la tasa de producción de fibrinógeno debido a la liberación de los gránulos de las plaquetas, k5 es la tasa de producción de fibrinógeno en presencia de trombina, y k₆ es la tasa de consumo de trombina en presencia de fibrinógeno, igual a la tasa de producción de fibrinógeno por acción de la trombina.

De (A15) y (A16) se obtiene:

Adicionalmente, suponiendo que el nivel de concentración de protrombina es igual a la concentración de gránulos liberados por las plaquetas activadas se obtiene:

Utilizando (A17) y (A18) y reemplazando en las expresiones (A9) - (A15) se obtiene:

Reemplazando en (A7) y (A8) los resultados dados en (A19)-(A25) se obtiene:

En (A27) el parámetro d es igual a DF /DT. Las expresiones (A26) y (A27) conforman el modelo matemático adimensional de la reacción cinética de la trombina y el fibrinógeno. Los valores de las constantes d, g , k y d se obtienen mediante la estabilidad numérica de la solución, mediante análisis de la literatura y en los casos en los cuales no se encontraron referencias significativas se realizaron cálculos estimados tomando como base datos relacionados. Los valores de las constantes k₁ a k₆ se obtuvieron a partir de estos resultados.

• T_ref: Se ha establecido experimentalmente que el tiempo necesario para formar el coágulo final puede variar entre 0 y 20 minutos, dependiendo del tipo de lesión. En el caso de exodoncias, este tiempo es en promedio 10 minutos, aunque depende del procedimiento quirúrgico utilizado y las condiciones anatómicas del sujeto de prueba.^37,45 Para la simulación se tomó 10 minutos como el tiempo necesario para la coagulación de la interfase hueso-implante dental.
• L_ref: Corresponde a la mayor distancia entre el borde del hueso y el perfil acanalado del implante. De acuerdo con,³⁵ la cantidad de tejido necrótico producto del procedimiento quirúrgico de inserción del implante es de unos 0.2mm. Considerando un implante con pasos de rosca de 0.35mm de espesor, el valor del parámetro es 0.55mm.
• T_ref: La formación del coágulo se debe a la presencia de 10 a 20 nmol/L de trombina.⁴⁶ De acuerdo con esto, y teniendo en cuenta que el peso molecular de la trombina es de 33.7 KDa.³¹ la concentración de trombina es en promedio 0.5055 g/ml.
• F_ref: La concentración promedio de fibrinógeno en plasma es de 7.600nM, es decir, 2.600 g/ml.¹²
• C_ref: La concentración de protrombina es de 100 g/ml.¹² Teniendo en cuenta este valor y los valores encontrados para las concentraciones de fibrinógeno y trombina, se escoge como valor del parámetro un valor medio de concentración, es decir, 1.000 g/ml.
• D_T: La constante de difusión de la trombina es 8.76x10-5 mm2/s.³¹ Sin embargo, de acuerdo a la expresión (A9) el valor del parámetro debe ser 5.0417x10-4 mm2/s, resultado que fue finalmente usado.
• D_F: Utilizando la ecuación de difusión de Einstein, tomando el radio de la molécula de fibrinógeno del orden de 10 ų² y la viscosidad de la sangre igual a 0.0038 Pa s,³³ se obtiene una constante de difusión de fibrinógeno de 5.647 x10-5 mm²/s.
• d: De la expresión (A17) el valor del parámetro es igual a DF /DT. Realizando esta operación se obtiene d=0.1120. No obstante, pruebas numéricas garantizan estabilidad del modelo al usar el valor 0.08.
• d: A partir de resultados experimentales el factor de conversión de la protrombina en trombina es del orden de ng/ml.s.⁴⁶ De acuerdo a esto el valor del parámetro se estimó en 1.2.
• g : Este parámetro está relacionado con la cantidad de fibrinógeno que es liberado por las plaquetas activadas durante la coagulación. Pruebas experimentales han permitido establecer que 1011 plaquetas liberan entre 3 y 25 mg de fibrinógeno.⁴⁷ Según ensayos de activación plaquetaria, en una concentración de plaquetas de 200x109 células por litro la tasa de activación es de 0.128 %/minuto.³⁰ Ajustando la concentración de plaquetas al valor normal (300x10⁹ células por litro²²) y al porcentaje de activación, el factor de aumento en la concentración de fibrinógeno debido a la activación de las plaquetas ( ) es de 225 ng/ml.s. Realizando la adimensionalización, y teniendo en cuenta que el 10 % del fibrinógeno está presente en los gránulos liberados por las plaquetas [28], el parámetro es igual a 0.052. Para las simulaciones éste valor se ajustó a 0.03.
• k: Este parámetro se obtiene dividiendo el factor de activación de fibrinógeno entre la concentración promedio de fibrinógeno, equivalente a la tasa de consumo de trombina. Usando los valores para fibrinógeno ya discutidos, y teniendo en cuenta la discusión para el valor del factor de activación , el valor del parámetro adimensional buscado se encuentra en el rango 0.03 - 0.138. El valor usado es 0.06.

La ecuación (3) se implementó en su forma dimensional. Los parámetros usados son los siguientes:

• f_max: En un coágulo formado con una concentración de fibrinógeno de 2.5 g/l sólo el 0.25% del volumen corresponde a fibrina. Es decir, en este coágulo 0.25 g de cada 100 ml son fibrina [29], lo que equivale a una concentración de 2.5 mg/ml.
• a: La tasa de polimerización de un monómero de fibrina es en promedio 111 x10^-5 s.^-123 Una fibra de fibrina está compuesta por 100 o más protofibrillas y cada protofibrilla está compuesta por dos monómeros.³⁴ Asumiendo que en el coágulo las fibras en promedio tienen 200 protofibrillas cada una, la tasa de polimerización de una fibra de fibrina es de al menos 0.444 s^-1. En las simulaciones este valor se ajustó a 0.5 s^-1.
• e: Un estudio de la cinética de polimerización del fibrinógeno determinó su tasa de polimerización en 23x10-5 s^1-5.²³ Teniendo en cuenta la concentración promedio de fibrinógeno, su factor de activación se estima en 598 ng/ml s.
• b: Para el cálculo de este parámetro se definió la siguiente relación:    

                                                                                                 

• con e el factor de activación de la fibrina. Reemplazando los demás términos de la expresión, el valor del parámetro es 0.4 ml/mg. Sin embargo, la estabilidad de la ecuación (2) depende de la relación:

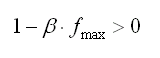
de donde se obtiene que b debe ser menor que 0.4. Por esta razón el valor del parámetro finalmente utilizado en las simulaciones es 0.37.

• w: Se asume que la formación de la red de fibrina hereda el patrón de transformación del fibrinógeno a medida que éste evoluciona en el tiempo. Para mantener esto, la función de activación de fibrina está referenciada al valor medio de concentración del fibrinógeno, es decir, 2.5 mg/ml. Realizando la corrección de unidades, el valor del parámetro es 1.
• p: Diferentes pruebas numéricas permitieron establecer un rango para este parámetro entre 10 y 30. Para disminuir el gasto computacional se prefirió usar el valor p=10.

APÉNDICE B

Los siguientes son los parámetros usados en la simulación de trombocitosis. Los parámetros que no se discuten a continuación conservan los valores mencionados en el apéndice A.

• g : Para el caso de trombocitosis se supone una concentración de plaquetas igual a 1.000 x10⁹ células por litro.⁴⁰ Con base en los resultados experimentales de la activación de las plaquetas³⁰ y realizando el ajuste en la concentración y el porcentaje de activación, se obtiene para el valor 2.500 ng/ml.s. Realizando la adimensionalización el valor del parámetro buscado es 0.577. Sin embargo, este valor causa saturación de la solución numérica. Comparando este valor con el encontrado para el caso de concentración normal de plaquetas se observa una diferencia de un orden de magnitud. Para garantizar esta diferencia y evitar la saturación el valor del parámetro usado es 0.1.
• b: A partir de la expresión (A28) y el valor de calculado para trombocitosis, el nuevo valor para es 4.4548. No obstante, este valor está por fuera del rango de estabilidad definido por la expresión (A29), razón por la cual se conserva el valor de igual a 0.37.

APÉNDICE C

Los siguientes son los parámetros usados en la simulación de trombocitopenia. Los parámetros que no se discuten a continuación conservan los valores mencionados en el apéndice A.

• g : Para el caso de trombocitopenia se supone una concentración de plaquetas igual a 20x10⁹ células por litro.^17,39 Con base en los resultados experimentales de la activación de las plaquetas³⁰ y realizando el ajuste en la concentración y el porcentaje de activación, se obtiene para el valor 3.33 ng/ml.s. Realizando la adimensionalización el valor del parámetro buscado es 7.7x10^-4. En las simulaciones el valor usado es 8.0x10^-4
• b: A partir de la expresión (A28) y el valor de calculado para trombocitopenia, el nuevo valor para es 5.9x10^-3. En las simulaciones el valor usado es 5.2x10^-3.

 

 

Aprobado: 20 de junio de 2009

 

 

Juan Carlos Vanegas A. Universidad Nacional de Colombia. Bogotá, Colombia. Edificio 407, oficina 103A. E-mail: [e-mail]