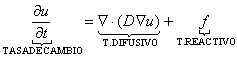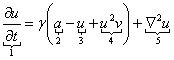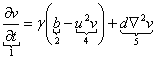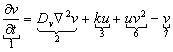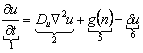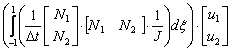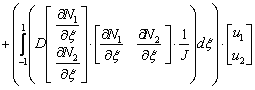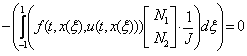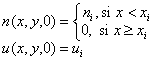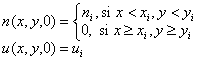ARTÍCULOS ORIGINALES

 

Implementación de modelos biológicos de reacción-difusión mediante el método de los elementos finitos

Implementation of reaction-diffusion biological models using the finite elements method

 

 

Juan. C.Vanegas Acosta^I; Nancy S. Landinez Parra^I; Diego A. Garzón-Alvarado ^II

^I Maestría en Ingeniería Biomédica. Grupo de Modelado Matemático y Métodos Numéricos GNUM. Universidad Nacional de Colombia, sede Bogotá. Colombia.
^II Grupo de Modelado Matemático y Métodos Numéricos GNUM. Departamento de Ingeniería Mecánica y Mecatrónica, Facultad de Ingeniería.Universidad Nacional de Colombia, sede Bogotá. Colombia.

 

 

---

RESUMEN

Distintos modelos matemáticos han sido formulados para describir la formación biológica de patrones espacio-temporales. Estos modelos matemáticos son solucionados computacionalmente mediante diversas técnicas numéricas entre las que se destacan el método de diferencias finitas y el método de los elementos finitos. El objetivo de este trabajo es presentar la implementación por elementos finitos de un modelo de morfogénesis, un modelo de formación de patrones y un modelo de movimiento celular. Los resultados obtenidos son comparables con los reportados en otros trabajos usando otros métodos numéricos. Se concluye que la técnica utilizada es válida para implementar este tipo de problemas y se espera sea de utilidad en la formulación e implementación de modelos matemáticos biológicos complejos de crecimiento y desarrollo celular y tisular.

Palabras clave: reacción-difusión, modelos biológicos, método de los elementos finitos, métodos numéricos, biología matemática.

---

ABSTRACT

Several mathematical models have been formulated to describe the biological formation of spatial-temporal patterns. These mathematical models are computationally solved using a wide set of numerical methods among which the finite differences method and the finite elements method are preferred. The aim of this work is to present the finite elements method implementation of a morphogenesis model, a pattern-formation model, and a cell-movement model. The results obtained are similar to those reported by other authors using other numerical approaches. This fact proves the technique to be suitable in the solution of these kind of models and supports our expectations for its use in the solution of complex biological models of growth and cell and tissue development.

Keywords: reaction-diffusion, biological models, finite elements method, numerical methods, mathematical biology.

---

 

 

INTRODUCCIÓN

El modelado matemático de problemas de biología del desarrollo ha permitido la formulación de modelos en cuya solución se encuentra la formación de patrones espacio-temporales.¹ Estos modelos pueden clasificarse como modelos de patrones químicos y modelos de patrones de movimiento celular. A su vez, en la categoría de los modelos de patrones químicos existen dos tipos de modelos: modelos de gradiente y modelos de reacción-difusión.²

Los modelos de gradiente son aquellos que generan patrones a partir de sustancias químicas que experimentan diferencias de concentración y que durante su evolución temporal tienden a un estado uniforme en el espacio y en el tiempo.² Por su parte, en los modelos de reacción-difusión, las interacciones químicas generan patrones complejos en el espacio y/o el tiempo, debido a que se encuentran términos de transporte, síntesis y degradación que dependen de todas las sustancias químicas presentes en el dominio de análisis.^2,3 Por el contrario, los modelos de movimiento celular involucran la formación de patrones debido a cambios de densidad celular debido a procesos de agregación o repulsión entre las células, o por respuesta a sustancias químicas concretas.³

En general, existen dos tipos de soluciones de estos modelos matemáticos: los patrones espacio-temporales y las ondas viajeras.^2,3 En 1952 A. Turing⁴ demostró que un modelo de reacción difusión con los parámetros apropiados y definido por un dominio espacial cerrado y extenso, evoluciona en un patrón espacial heterogéneo debido a pequeñas perturbaciones de las concentraciones químicas, fenómeno conocido como inestabilidad por difusión.^{2, 3, 6} Estas inestabilidades de Turing, a su vez, se caracterizan por presentar un estado temporal estable a medida que evoluciona en el tiempo, y por la formación de patrones inestables en el espacio, adecuados para describir problemas de morfogénesis. ^2,3,7,9 Por su parte, las solución de onda viajera representa, desde el punto de vista físico, procesos de transición de un equilibrio a otro que se adaptan a las propiedades del medio y generan un patrón de onda que se desplaza desde las condiciones iniciales.¹⁰

Estas soluciones han sido estudiadas en la biología del desarrollo debido a que permiten cuantificar la evolución de las distintas variables implicadas en el proceso de formación y crecimiento de los diversos tejidos, y porque es posible asociar la formación de patrones espacio-temporales y ondas viajeras a los fenómenos biológicos de desarrollo tisular.^2,3,5 Teniendo en cuenta la descripción general de los diferentes tipos de modelos biológicos, en el presente artículo se han considerado dos modelos químicos formulados a partir de ecuaciones de reacción difusión cuya respuesta presenta inestabilidades de Turing, y un modelo en cuya solución la onda viajera describe un proceso de movimiento celular. El objetivo es realizar una implementación numérica de estos modelos utilizando el método de los elementos finitos y comparar las soluciones con los resultados reportados por otros autores. ^1,2,3,8,11 En la sección 2 se hace una breve explicación de las ecuaciones de reacción difusión y en la sección 3 se presentan los modelos biológicos utilizados. El método de los elementos finitos mediante el cual estos modelos son implementados es presentado en la sección 4 y en la sección 5 se ilustran las soluciones numéricas obtenidas. Finalmente, en la sección 6 se discuten los resultados.

Ecuaciones de reacción-difusión

Un problema de difusión modela el movimiento de una densidad de individuos de una especie (bacterias, células, químicos) en un entorno cualquiera.^1,2,7 El movimiento de u(t,x), o término difusivo, indica los cambios en la concentración desde puntos de mayor concentración hacia puntos de menor concentración.^8,11,12 Este principio es conocido como Ley de Fick y se expresa de la siguiente forma (1):⁸

(1)

donde J es el vector de flujo de u(t,x), y D es el coeficiente de difusión.

A su vez, la reacción entre dos o más sustancias establecen un término reactivo adicional en la función de concentración u(t,x) denotado por f(t,x,u). De acuerdo al principio de conservación, la razón de cambio de la cantidad de materia contenida en un volumen V debe ser igual al flujo neto de materia a través de la superficie S que la delimita, más la cantidad de materia transformada al interior de V debido al término reactivo. Esto expresado matemáticamente es (2):

    (2)

En (2) es el vector normal a la superficie S. Utilizando el teorema de la divergencia en el término difusivo y combinando (1) y (2) se obtiene (3):

La ecuación (3) corresponde a una ecuación integral definida en el dominio ?=V con condiciones de contorno definidas por la superficie =S que rodea al volumen V. Para garantizar que el patrón espacial formado se deba únicamente a la organización al interior del contorno, y no a flujos externos, se deben asumir condiciones de flujo en el contorno iguales a cero [6]. Expresando (3) en forma diferencial se obtiene (4): ²

  (4)

La ecuación (4) se conoce como ecuación de reacción-difusión y permite, junto con las condiciones de contorno dadas, predecir la evolución de los individuos de la especie denotada por u(t,x). Aunque el análisis anterior es válido para un sistema de una única especie de individuos, el resultado puede extenderse a un sistema de varias especies de individuos denotando u(t,x) como u(t,x). ^2,6,8

Modelos implementados

Existen diferentes modelos biológicos que permiten obtener una descripción matemática de fenómenos complejos presentes en la naturaleza.^{1, 3, 5, 8, 11} Dos modelos bien referenciados, formulados por ecuaciones de reacción difusión, son el modelo de Schnakenberg, o modelo de morfogénesis,1, 2, 8, 11 y el modelo de glucólisis,2, 8, 9 utilizado para explicar la síntesis de glucosa en energía celular. Estos dos modelos generan patrones espaciales y cumplen con los criterios de estabilidad de Turing analizados por otros autores.⁹ Un tercer modelo típicamente utilizado para ilustrar el movimiento celular consecuencia de la interacción química con el entorno es el modelo de quimiotaxis.^{7, 8} Este modelo tiene como solución una onda viajera.

Modelo de Schnakenberg

El modelo de Schnakenberg determina el comportamiento de un químico activador u en presencia de un químico inhibidor v. 1, 2 En su forma adimensional, el modelo está descrito por las siguientes ecuaciones (5):²

   (5a)

      (5b)

En la ecuación (5) el término 1 representa flujo, 2 representa producción, 3 representa consumo, 4 representa catálisis no lineal, y 5 representa difusión. Las constantes a, b, d y son todas parámetros positivos, con a y b valores adimensionales de producción, una constante adimensional y d un valor de difusión.^{2, 8} La reacción cinética es tal que en la ecuación (5a) el término 4 representa la producción de u en presencia de v, en tanto que en la ecuación (5b) el mismo término representa el consumo de v en presencia de u. El modelo se utiliza como base matemática para análisis de estabilidad y formación de patrones,2, 9 en la predicción de la interacción entre sistemas químicos moleculares 2, 11 y en la morfogénesis de formación y crecimiento de hueso. ^{2, 13}

Modelo de Glucólisis

La glucólisis o glicólisis es el proceso de síntesis de la molécula de glucosa para proporcionar energía al metabolismo celular. A través de una secuencia de reacciones, la glucosa es transformada en piruvato y en ATP, unidad de intercambio metabólico en el organismo vivo [8]. Este proceso se describe matemáticamente en forma adimensional mediante las siguientes ecuaciones (6):^2,8

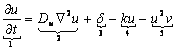    (6a)

   (6b)

En la ecuación (6) el término 1 representa flujo, 2 representa difusión, 3 representa producción, 4 representa degradación, 5 representa consumo no lineal, 6 representa activación no lineal, y 7 representa consumo. La interpretación biológica es similar al modelo de Schnakenberg, con u la concentración de glucosa, v la producción de piruvato, Du y Dv los coeficientes de difusión, el término u2v representando consumo no lineal de u y el término uv2 representando la activación no lineal de v. es un parámetro positivo que representa la constante de formación de glucosa. El parámetro k, también positivo, representa en (6a) el consumo natural de glucosa, mientras que en (6b) representa la producción, en la misma proporción, de piruvato. Este modelo representa la heterogeneidad de un tejido para la transformación de glucosa en piruvato simulando la realidad del fenómeno.2, 8

Modelo de Quimiotaxis

La quimiotaxis es el fenómeno de migración celular en el cual las células dirigen su movimiento conforme a gradientes de concentración de ciertos químicos presentes en el entorno celular denominados quimioatractantes.^{7, 8} Un modelo de este fenómeno describe el movimiento celular como una onda viajera controlada por la concentración del quimioatractante.⁸ Como este movimiento celular puede ocurrir conjuntamente con procesos de división mitótica y pérdida celular, el modelo completo es descrito por las siguientes ecuaciones (7):⁸

   (7a)

     (7b)

En (7), n es la densidad celular, u es la concentración de quimiotractante, Du y Dv son los coeficientes de difusión, n es la sensibilidad al quimioatractante, n es la tasa de degradación natural celular, u es la tasa de degradación química celular y g(n) es una función de la producción de quimioatractante por parte de las células. El término 1 representa flujo, 2 representa difusión, 3 representa quimiotaxis, 4 representa mitosis celular, 5 representa producción dependiente, y 6 representa degradación. En la siguiente sección se presenta la técnica de solución numérica utilizada para implementar los modelos anteriores mediante el método de los elementos finitos.

Solución por el método de los elementos finitos

El empleo del método de los elementos finitos permite transformar el sistema de ecuaciones diferenciales parciales que conforma cada modelo presentado en un sistema de ecuaciones diferenciales ordinarias respecto del tiempo.^{2, 14, 15} El método que se presenta se implementa mediante una rutina de usuario programada de forma particular para cada modelo, cuyo fundamento matemático se encuentra en el método de ponderación de los residuos. ^{16, 17, 18}

Sea un dominio divido en cierto número NE de elementos, cada uno definido como un subdominio e de . Para cada e existe un residuo Re o error entre la solución numérica local y la solución exacta. Si se toma la suma de los residuos locales, es posible obtener un residuo global Rg y una solución global del problema definido en el dominio . Para el caso unidimensional de la ecuación de reacción difusión expresada en (4), se quiere que el error en el dominio cumpla con la relación (8):¹⁶

(8)

(9)

(10)

Resolviendo la integral para cada uno de los términos, haciendo integración por partes en el segundo término, y teniendo en cuenta condiciones de contorno nulas, se obtiene (11):

(11)

donde es el contorno del dominio . La evaluación de (11) en cada subdominio e o elemento da lugar a la expresión (12):

(12)

Si u1 y u2 son los valores de u(t,x) en los nodos 1 y 2 de un elemento cualquiera, la variación lineal o interpolación entre estos dos valores a lo largo de dicho elemento está dada por (13):¹⁸

(13)

En (13) N1 y N2 son las funciones de interpolación definidas para cada elemento que constituyen la base para la construcción de una solución continua, también conocidas como funciones de forma.^{17, 18} Estas funciones están definidas en el intervalo con una variable de normalización. Esto garantiza que las funciones de forma sean independientes de las coordenadas nodales de cada elemento, lo que permite su extensión a todos los elementos del dominio [16]. Definiendo la variable x como una interpolación de los valores nodales de x para un elemento con nodos en las coordenadas x1 y x2 se obtiene (14): ¹⁸

(14)

Utilizando el método de Bubnov-Galerkin, más conocido como método de Galerkin, según el cual las funciones de ponderación son iguales a las funciones de forma, 16, 17, 18 cambiando el espacio de integración de la variable x a la variable mediante el jacobiano (J) de la transformación y ajustando la notación vectorial, la expresión (12) puede reescribirse como (15):

    (15)

En (15) la función f es el término reactivo de la expresión (4). La expresión (15) puede reducirse a un sistema matricial de tipo elemental expresado como (16): ^{14, 15, 18}

La expresión (16) corresponde a la discretización algebraica en el dominio e de un elemento, con k la matriz de rigidez elemental, u las incógnitas y f el término independiente. Ensamblando el resultado de (15) para el total NE de elementos en 16, 18 se obtiene un sistema matricial general definido como (17):^{14, 15, 18}

K U = F     (17)

En (17) K es la matriz global de rigidez, U es el vector de incógnitas y F es el vector global de entradas. Este método matemático es aplicable a problemas de mayor dimensión. Una formulación para problemas bidimensionales y tridimensionales puede encontrarse en las propuestas que hacen otros autores. ^{2, 14, 16}

 

RESULTADOS

Las soluciones numéricas presentadas se obtuvieron utilizando la metodología presentada en la sección 4. El hardware utilizado es un PC de escritorio con procesador AMD Athlon 64 de 2.4 GHz y 1 GB de memoria RAM.

Modelo de Schnakenberg

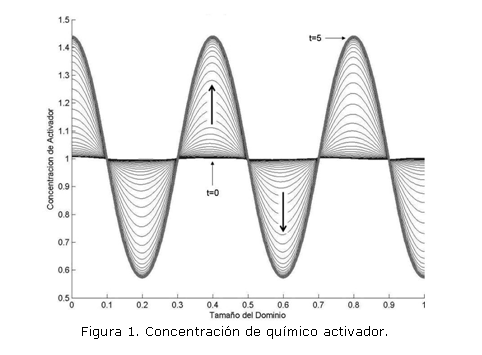
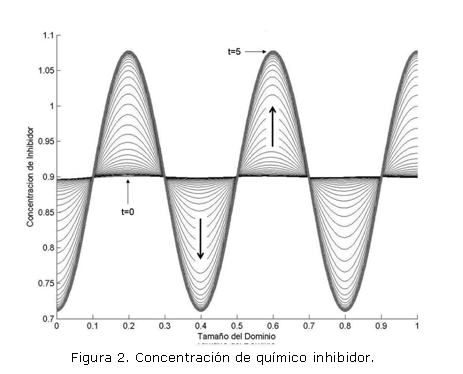
Los resultados para el modelo descrito por las ecuaciones (5) en el dominio unidimensional [0,1] se muestran en las figuras 1 y 2. En la implementación se usaron los siguientes parámetros: a=0.1, b=0.9, d=10, =789. Las condiciones de flujo en el contorno se consideran iguales a cero (flujo nulo). Se realizan 1.000 iteraciones, con un paso de tiempo t=0.005, se utilizan 300 elementos cuadráticos lagrangianos y 601 nodos. Las flechas en las figuras señalan la dirección hacia la cual evoluciona la respuesta hasta alcanzar el estado espacial estable. La condición inicial corresponde a una perturbación del 5% alrededor del estado temporal estable.

 

 

Una implementación adicional en el dominio bidimensional [0, 1] permite obtener la formación de patrones espacio-temporales mostrada en la figura 3. Los parámetros usados son: a=0.1, b=0.9, d=9.1676, =176.72. Se realizaron 100 iteraciones con un paso de tiempo t=0.05. Se utilizaron 625 elementos cuadriláteros bilineales.16 Las condiciones de flujo en el contorno se consideran iguales a cero. Los resultados muestran la evolución temporal de la formación del patrón espacial del químico activador. En la figura 4, a) es la condición inicial, dada por un nivel de perturbación del 5% alrededor del estado temporal estable, b) respuesta en t=1, c) respuesta en t=2, y d) respuesta en t=5.

Los resultados muestran el patrón inestable espacial del modelo. Además, la respuesta del modelo en el caso unidimensional muestra el desfase de 180° del químico activador respecto al inhibidor, lo que indica la acción de éste último sobre la producción del primero. En el caso bidimensional se presenta el mismo tipo de solución desfasada, pero por simplicidad, no se muestra la solución del modelo para la ecuación del químico inhibidor. Adicionalmente, el modelo permite confirmar que pequeñas perturbaciones son determinantes en la formación de patrones espaciales.1, 2, 6, 9 Los resultados mostrados están en completa concordancia con los resultados reportados utilizando para la implementación otros métodos numéricos. ^{1, 2, 8}

Modelo de Glucólisis

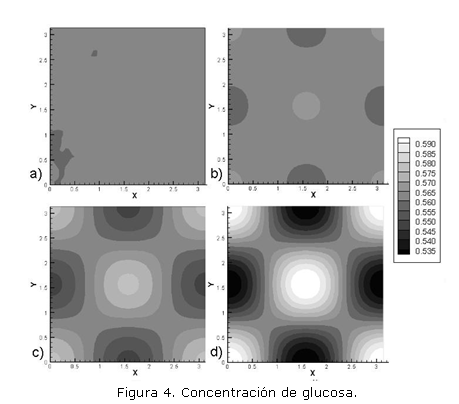
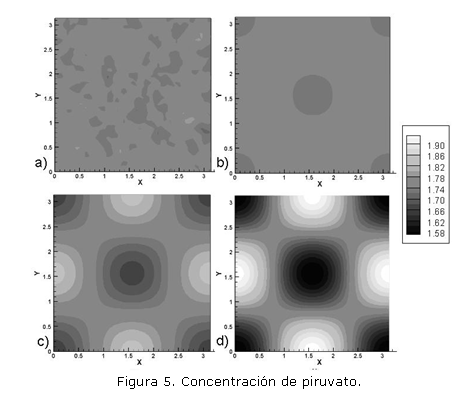
El modelo descrito por las ecuaciones (6) fue solucionado en el dominio bidimensional [0, ] x [0, ] utilizando los siguientes parámetros: Du=1.0, Dv=0.0518, =1.75, k=0.05. Se realizaron 25.000 iteraciones con un paso de tiempo t=0.1. Se utilizaron 2.500 elementos cuadriláteros bilineales. Las condiciones de flujo en el contorno se consideran iguales a cero. Las figura 4 y 5 muestran el resultado obtenido para la concentración de glucosa (químico activador) y la concentración de piruvato (químico inhibidor) donde a) es la condición inicial, dada por un nivel de perturbación del 5% alrededor del estado temporal estable, b) respuesta en t=750, c) respuesta en t=1.500, y d) respuesta en t=2.500.

 

 

Se observa el patrón inestable espacial del modelo y la respuesta en desfase de 180° entre las dos concentraciones debido a la relación consumo-producción entre los agentes químicos. Las diferencias de intensidad se deben a que el consumo de glucosa es mayor que la producción de piruvato.

Utilizando un dominio bidimensional [0,5 ] x [0,5 ] con una malla de 2.500 elementos cuadriláteros bilineales, los parámetros antes usados, y manteniendo las condiciones de la simulación del caso anterior, se obtiene el patrón de puntos mostrado en la figura 6, con a) la condición inicial, dada por un nivel de perturbación del 5% alrededor del estado temporal estable, b) respuesta en t=750, c) respuesta en t=1.500, y d) respuesta en t=2.500.

Finalmente, usando el dominio bidimensional [0,5 ] x [0,5 ] con una malla de 2.500 elementos cuadriláteros bilineales, se establecen para los parámetros los valores Du=1.0, Dv=0.08, =1.2, k=0.06, y se realizan 100.000 iteraciones con un paso de tiempo t=0.1, se obtiene el patrón de franjas mostrado en la figura 7, donde a) la condición inicial, dada por un nivel de perturbación del 5% alrededor del estado temporal estable, b) respuesta en t=50, c) respuesta en t=150, y d) respuesta en t=300.

Modelo de Quimiotaxis

El modelo de quimiotaxis dado por las ecuaciones (7) fue implementado utilizando un dominio bidimensional de dimensiones [0,1] x [0,1] con una malla de 2.500 elementos cuadriláteros bilineales y un total de 800 iteraciones con un paso de tiempo de t=0.01 Los parámetros utilizados son: Du= 0.001, Dv= 0.005, ?= 2, u= 0.05, v= 0.05, =0.001, p=30, r=4. La función f(u) es un escalón unitario que ha sido aproximado por la expresión (18):

    (18)

Por su parte, la función g(n) es un escalón unitario que ha sido aproximado por la expresión (19):

(19)

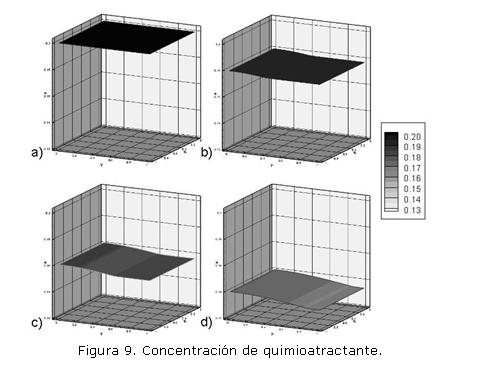
En (18) y (19) n0 y u0 son los puntos de activación. Los valores utilizados son: n0=0.01 y u0= 0.0195. Las condiciones de flujo en el contorno se consideran iguales a cero. Las figuras 8 y 9 muestran los resultados obtenidos donde a) es la condición inicial, b) es la respuesta en t=2.5, c) es la respuesta en t=5, y d) es la respuesta en t=8. La condición inicial en a) está dada por (20), con ni=1.0, xi=1.0, y ui=0.2.

(20)

 

 

Finalmente, se modificó la condición inicial en (20) de la siguiente manera (21):

(21)

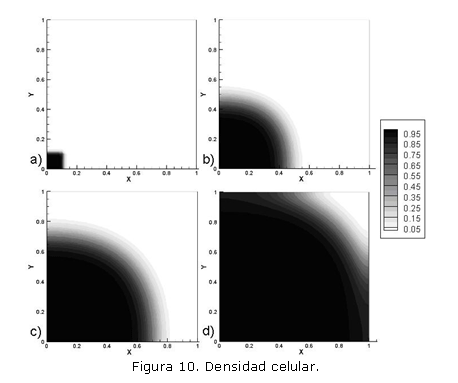
Usando (21) con ni=1.0, xi=1.0, yi=1.0 y ui=0.2, los demás parámetros como en el caso anterior y un total de 200 iteraciones con un paso de tiempo de t=0.05 se obtuvo la solución mostrada en la figura 10 donde a) es la condición inicial, definida por (21), b) es la respuesta en t=50, c) es la respuesta en t=75, y d) es la respuesta en t=10.

Las dos implementaciones del modelo de quimiotaxis se ajustan a los resultados obtenidos mediante el método de diferencias finitas reportado por Oñate.8 Se comprueba además la formación del patrón de onda viajera que representa el llamado químico que el quimioactractante ejerce sobre las células, y tal como se aprecia en las figuras 8 y 10, es posible ajustar las condiciones iniciales para obtener resultados variables. Este hecho es significativo para la formulación de modelos específicos en problemas de crecimiento y desarrollo celular y tisular, donde los procesos de diferenciación y proliferación tienen lugar en zonas definidas.

 

DISCUSIÓN

Los modelos matemáticos implementados muestran cómo las ecuaciones de reacción difusión son de utilidad para representar la formación de patrones en sistemas biológicos. Se ha evidenciado la existencia de inestabilidades espaciales debido a pequeñas perturbaciones del estado temporal estable y las variaciones de dichas inestabilidades conforme a los parámetros de cada modelo.

La implementación del modelo de Schnakenberg permite visualizar esta formación de patrones espaciales y la evolución en el tiempo de esta formación. Un análisis de los parámetros puede hacerse para identificar características de la formación del patrón, el modo de la onda, y el valor de estado estable.2, 9 La implementación unidimensional del modelo de Schnakenberg es complementada con su implementación bidimensional, con lo que se comprueba la validez del método para la solución de problemas de dimensión superior.

En el modelo de glucólisis se hace más evidente la variación del patrón espacial inestable conforme a los valores dados a los parámetros del modelo, tal como se observa en las figuras 4, 6 y 7. Se observa además el efecto de la dimensión del dominio en la formación del patrón, especialmente en relación con el dominio bidimensional [0, ] x [0, ] de las figuras 4 y 5, y el dominio bidimensional [0,15] x [0,15] de las figuras 6 y 7, hecho que ha sido ampliamente analizado por otros autores.^{1, 14} En términos computacionales, estas variaciones del dominio, en conjunto con la elección adecuada de parámetros, inducen a que la solución requiera de un menor número de iteraciones pasos de tiempo menor, como en el caso del resultado de la figura 7. La escogencia de los parámetros esta asociada a las características de inestabilidad de Turing del modelo y una análisis matemático detallado de la inestabilidad conduce a parámetros ajustados.⁹ Para efectos de formación morfogénica como en el caso de redes fibrilares, el resultado mostrado en la figura 7 se ajusta no sólo en cuanto al patrón espacio sino en términos de su velocidad de estabilidad temporal, ya que sólo requiere de 300 unidades de tiempo para alcanzar su estado estable. Por su parte los resultados de las figura 3, 4, 5 y 6 pueden ser asociados a la formación de patrones de pigmentación o a patrones de formación ósea. ^{2, 3, 8}

El modelo de quimiotaxis, por su parte, se presenta como un ejemplo de los fenómenos de movimiento y transporte celular. En particular, los resultados permiten evidenciar la obtención de un patrón espacial que semeja el movimiento de un contingente celular en respuesta a una concentración de quimoatractante. Estos frentes de onda son apreciables en las figuras 8 y 10. El resultado de este movimiento celular es la reducción en el nivel de quimioatractante mostrado en la figura 9 y que denota el consumo necesario para generar el movimiento del frente celular.⁸ Un desarrollo más notorio de este movimiento es el objeto de la figura 10, donde la condición inicial se ha limitado a un cuadrado de [0,2] x [0,2] en la esquina inferior izquierda del dominio. El resultado muestra el movimiento de la concentración celular a partir del cuadro de condición inicial. Conforme el contingente inicial de células se desplaza, la concentración final aumenta producto del término mitótico en (7), lo cual explica la aparente homogeneidad a lo largo del dominio. A su vez, el término difusivo en (7) controla la dirección del movimiento celular y garantiza que el frente de onda tenga un patrón de desplazamiento radial desde la región de condición inicial.^{2, 6}

De los resultados obtenidos se concluye que la implementación los modelos biológico presentados mediante la formulación matemática y el método numérico por elementos finitos descritos anteriormente permite reproducir los resultados obtenidos por otros autores.^{1, 2, 8, 11} La técnica empleada permite solucionar modelos complejos con menor costo computacional y mejor aproximación numérica, siempre que el dominio, el mallado y las características temporales sean bien especificados. Se espera que la evidencia de los resultados presentados y la técnica de solución empleada sean de utilidad en la formulación e implementación de modelos matemáticos biológicos complejos de crecimiento y desarrollo celular y tisular.

 

AGRADECIMIENTOS

Los autores agradecen a Dirección de Investigación de la Universidad Nacional de Colombia Sede Bogotá por el apoyo económico a los proyectos de investigación en posgrado. Este trabajo hace parte del proyecto de investigación 202010011460 financiado con recursos de la convocatoria DIB Programas de Posgrado 2008 de la Universidad Nacional de Colombia.

 

REFERENCIAS BIBLIOGRÁFICAS

1. Madzvamuse A, Wathen AJ, Maini PK. A moving grid finite element method applied to a model biological patter generator. Journal of Computational Physics 2003; 190: 478-500.

2. Garzón DA. Simulación de procesos de reacción-difusión: aplicación a la morfogénesis del tejido óseo [Tesis de Doctorado]. Zaragoza, España, 2007: 17-70.

3. Maini PK. Using mathematical models to help understand biological pattern formation. C. R. Biologies 2004; 327: 225-234.

4. Turing AM. The chemical basis of morphogenesis. Philos. Trans. Roy. Soc. 1957; 237: 37-72.

5. Page K, Maini PK, Monk NAM. Pattern formation in spatially heterogeneous Turing reaction diffusion models. Physics D. 2003; 181: 80-101.

6. Murray JD. Mathematical Biology II. Spatial models and biomedical applications. Springer-Verlag, 1993: 75-97.

7. [7] J. D. Murray. Mathematical Biology I. An introduction. Springer-Verlag. 2002. 405-509.

8. Painter KJ. Chemotaxis as a mechanism for morphogenesis [PhD Thesis]. United Kingdom: Oxford University, 1997: 3-25.

9. Vanegas A, Landinez P, Garzón-Alvarado DA. "Análisis de la inestabilidad de Turing en modelos biológicos". Revista DYNA, Universidad Nacional de Colombia - Medellín. Aprobado para publicación. 2009.

10. Wang ZC, Li WT, Ruan S. Travelling wave fronts in reaction-diffusion systems with spatio-temporal delays. J. Differential Equations 2006; 222: 185-232.

11. Maini PK. Spatial pattern formation in chemical and biological systems. J. Chem. Soc., Faraday Trans. 1997; 93 (20): 3601-10.

12. Murray JD, Ester GF. Cell traction models for generation pattern and form in morphogenesis. J. Math. Biology 1984; 19: 265-79.

13. Izaguirre JA, Chaturvedi R, Huang C, Cickovski T. Compucell, a multi-model framework for simulation of morphogenesis. Bioinformatics 2004; 20: 1129-37.

14. Madzvamuse A. A numerical approach to the study of spatial pattern formation. [PhD Thesis]. Oxford, UK, Computing Laboratory. University of Oxford, 2000: 10-40.

15. Crampin E. Reaction diffusion patterns on growing domains [PhD Thesis]. Oxford, UK, Magdalen College. University of Oxford, 2000: 1-34.

16. Rao S. The finite element method in engineering. Elsevier Science and Technology Books, 2004: 53-112.

17. Oñate E, Miquel J, Zárate F. Stabilized solution of the multidimensional advection-diffusion-absorption equation using linear finite elements. Computers and Fluids 2007; 36: 1-111.

18. Oñate E. Cálculo de estructuras por el Método de los Elementos Finitos. CIMNE, España, 1992: 1-99.

 

 

Recibido: 3 de septiembre de 2009
Aprobado: 30 de septiembre de 2009

 

 

Juan. C.Vanegas Acosta. Grupo de Modelado Matemático y Métodos Numéricos GNUM. Universidad Nacional de Colombia, sede Bogotá. Colombia.