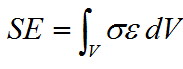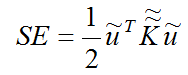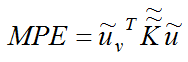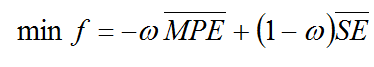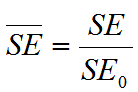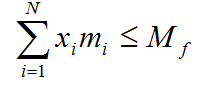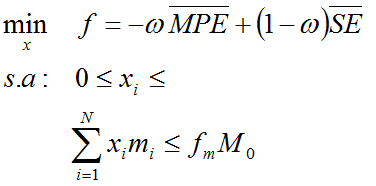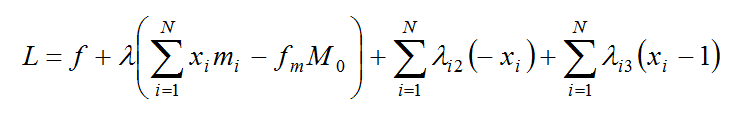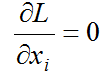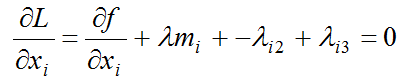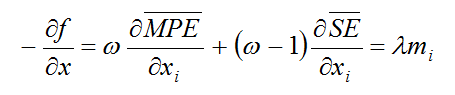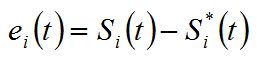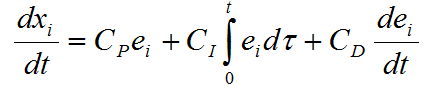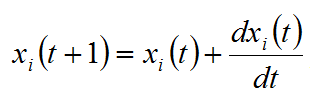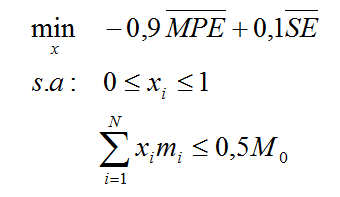ARTÍCULOS ORIGINALES

 

Síntesis topológica de mecanismos flexibles para aplicaciones biomédicas

Topology synthesis of feasible for biomedical applications

Carlos Alberto Narváez^I; Diego Alexander Garzón-Alvarado^II

^IAsistente. Departamento de Ingeniería Mecánica y Mecatrónica. Universidad Nacional de Colombia.
^IIDoctor en Ciencias (PhD), Máster en Ciencias, Ingeniero Mecánico. Profesor Adjunto. Facultad de ingeniería. Universidad Nacional de Colombia, Bogotá.

---

RESUMEN

Los mecanismos flexibles son dispositivos mecánicos diseñados para transformar desplazamientos, fuerzas o energía a través de la flexibilidad de sus elementos estructurales. Sus ventajas frente a los mecanismos de eslabones rígidos con juntas pinadas los convierten en una alternativa viable para el diseño de BioMEMS, ya que son sistemas que requieren alta precisión de movimiento a escalas de tamaño muy reducidas. El diseño de mecanismos flexibles puede realizarse con el empleo de técnicas de optimización estructural, es la optimización topológica la más empleada. En investigaciones previas se desarrolló un nuevo método de optimización topológica inspirado en el proceso de regeneración ósea conocido como el Método de los autómatas celulares híbridos, el cual demostró su aplicabilidad y eficiencia computacional en la síntesis topológica de estos dispositivos. El objetivo de este artículo es extender el método a la síntesis de mecanismos flexibles para aplicaciones biomédicas, específicamente, para el diseño de una micropinza para manipulación de fibroblastos. La topología óptima obtenida corresponde con los diseños referidos en otras investigaciones. Los resultados permiten llevar a cabo la manufactura del dispositivo gracias a que no presentan juntas de facto o patrones de tablero de ajedrez, que son errores típicos en la solución de problemas de optimización topológica mediante otros métodos de solución.

Palabras clave: BioMEMs, mecanismos flexibles, optimización topológica, autómatas celulares híbridos.

---

ABSTRACT

Feasible mechanisms are mechanical devices designed to transform displacements, strengths or energy through flexibility of its structural elements. Its advantages versus rigid links mechanisms with pinnate joints becoming a viable alternative for the BioMES design since they are systems requiring high movement accuracy at very reduced scale level. The feasible mechanisms design may be carried out using structural optimization techniques where that of topology type is the more used. In prior researches we developed a new topology optimization method inspired in the bone regeneration process known as the Method of hybrid cellular automaton, which showed its applicability and computer effectiveness in the topology synthesis of these devices. The aim of present paper is to spread the method to feasible mechanisms synthesis for biomedical publications, specifically, for the design of a microclamp for the fibroblasts management. Optimal topology achieved is in correspondence with the designs mentioned in other researches. Results allow to carry out the manufacture of this device because of they haven't de facto joints or patterns in chessboard, which are typical errors to solve the topology optimization by means of other solutions methods.

Key words: BioMEMs, feasible mechanisms, topology optimization, hybrid cellular automaton.

---

 

 

INTRODUCCIÓN

Los sistemas micro-electro-mecánicos biomédicos (BioMEMS) pueden definirse como dispositivos o sistemas, construidos basados en las técnicas de fabricación micro/nano escalar, que son usados para procesar, transportar, manipular, analizar o construir entidades biológicas o químicas.¹ Desde la aparición de los sistemas micro-electro-mecánicos (MEMS) en 1987, se reportan importantes investigaciones en la implementación de estos dispositivos y su aplicación a la biomedicina, desde el desarrollo de equipos y herramientas terapéutica, de diagnóstico y quirúrgica,² órganos artificiales e implantes.³

En el diseño de BioMEMS son requerimientos frecuentes la alta precisión de movimiento a escalas de tamaño reducidas, la eliminación de holguras entre componentes, la disminución del desgaste debido a la fricción y la reducción de los procesos de manufactura y ensamble.⁴ Para satisfacer dichos requerimientos los diseñadores desarrollaron el concepto de los mecanismos flexibles, lo cuales obtienen su movilidad gracias a la flexibilidad de sus componentes y no de las juntas pinadas o de deslizantes presentes en las cadenas cinemáticas de eslabones rígidos.⁵

Los dos enfoques principales para diseñar mecanismos flexibles son la síntesis mediante modelos de cuerpo seudo-rígido, usada ampliamente por Howell,⁴ y la síntesis mediante técnicas de optimización estructural, empleada por Ananthasuresh,⁶ Pedersen, Buhl y Sigmund,⁷ entre otros autores. La síntesis mediante modelos de cuerpo seudo-rígido consiste en analizar un mecanismo de flexibilidad concentrada, compuesto por eslabones rígidos que están unidos mediante juntas pinadas con resortes de torsión, que permiten acumular y transformar energía a medida que se produce el movimiento. Cuando se considera al mecanismo como un continuo, que se deforma debido a las cargas aplicadas, es posible emplear técnicas de optimización estructural para obtener mecanismos de flexibilidad distribuida.

Entre las técnicas de optimización estructural la más empleada es la optimización topológica, cuyos métodos computacionales fueron introducidos inicialmente por BendsÆe.⁵ Recientemente Tovar⁸ ha desarrollado una metodología de optimización estructural denominada autómatas celulares híbridos (en inglés, HCA:hybrid cellular automata), la cual se inspira en el proceso de remodelamiento óseo y combina las reglas locales de los autómatas celulares (CAs) con el análisis estructural por elementos finitos.⁹ Esta nueva metodología demuestra su eficiencia para resolver problemas de optimización topológica¹⁰ y su aplicabilidad al diseño de mecanismos flexibles.^11,12

Las micropinzas son mecanismos flexibles cuyo diseño permite prensar objetos de tamaño muy pequeño, indispensables en actividades como el microensamble de componentes y la cirugía mínima invasiva. Su función más importante es prensar el objeto sin producirle daño alguno, por lo tanto la precisión en el movimiento de cierre de las pinzas y el control de la fuerza de apriete son requerimientos de diseño fundamentales.¹³ Estos sistemas pueden clasificarse de acuerdo al tipo de actuador que activa el movimiento de cierre. Las micropinzas con actuador piezoeléctrico son las más frecuentes.¹⁴ Varios ejemplos de diseño se encuentran referidos en la bibliografía desde los ejemplos de síntesis topológica por Ananthasuresh,⁶ Pedersen, Buhl y Sigmund,⁷ hasta los prototipos desarrollados recientemente por Zubir y Shirinzadeh,^13,14 Kohl y Krevet,¹⁵ Nah y Zhong,¹⁶ Tian, Shirinzadeh y Zhang,¹⁷ entre otros.

El objetivo de esta investigación es extender la metodología HCA a la síntesis topológica de mecanismos flexibles con aplicaciones biomédicas, a través del diseño de una micropinza para manipulación de fibroblastos. El algoritmo de optimización se implementó en MATLAB y se comunicó con el módulo estructural de ANSYS para realizar el análisis geométricamente no lineal por elementos finitos.

MÉTODOS

La presente investigación teórica se realizó de la siguiente manera: inicialmente se analizó la síntesis topológica para mecanismos flexibles con el empleo de la metodología HCA. Se definió la función objetivo y las restricciones del problema de optimización estructural. Luego se analizaron las condiciones de optimalidad para el problema de optimización y la deducción de la regla de evolución. Posteriormente se describió la implementación computacional que se realizó en MATLAB y se presentaron los resultados de la aplicación del algoritmo al diseño de la micropinza para manipulación de fibroblastos. Finalmente se procedió la discusión de los resultados, y se arribó a conclusiones que generaron campos futuros de investigación.

DESARROLLO

Síntesis topológica para mecanismos flexibles con el empleo del método HCA

El dominio de diseño para la síntesis de mecanismos flexibles se muestra en la figura 1. Se llevó a cabo el diseño de un mecanismo cuyo desplazamiento u_out en el puerto de salida, producido por la aplicación de una carga F_in en el puerto de entrada, sea máximo. Para simular el contacto entre el puerto de salida y la pieza sobre la cual actúa el mecanismo se agrega un resorte con rigidez k_s.

Existe una gran variedad de funciones, objetivos que se emplean en el diseño de mecanismos flexibles. En general todas ellas expresan una formulación de dos criterios, pues el mecanismo debe ser lo suficientemente flexible como para maximizar el desplazamiento de salida pero suficientemente rígido para soportar la carga aplicada.⁴

La rigidez del mecanismo puede cuantificarse a través de la energía de deformación (SE: strain energy). Maximizar la rigidez equivale a minimizar la energía de deformación. SE puede expresarse como

(1)

donde s y e son los campos de esfuerzo y deformación producidos por la fuerza de entrada. Si el dominio de diseño es discretizado en elementos finitos lineales, SE puede ser aproximada por

(2)

dondees el vector de desplazamientos producidos por la carga de entrada y la matriz de rigidez.

La flexibilidad del mecanismo puede cuantificarse a través de la energía potencial mutua (MPE: mutual potential energy). Maximizar la flexibilidad equivale a maximizar MPE, la cual puede expresarse como

(3)

donde s_d es el campo de esfuerzos producido por una carga unitaria virtual que se aplica en el puerto de salida en la misma dirección del desplazamiento que se desea. Al tener en cuenta la discretización del dominio de diseño en elementos finitos lineales, MPE puede aproximarse por

(4)

donde es el campo de desplazamientos producidos por la carga virtual.

Existen varias formulaciones matemáticas que combinan ambos objetivos en una sola función objetivo.⁴ En esta investigación se empleó la formulación lineal ponderada

(5)

donde w es el factor de ponderación cuyo valor se define a priori entre 0 y 1. y son los valores normalizados de MPE y SE, definidos como

(6a y 6b)

donde MPE₀ y SE₀ son los valores de MPE y SE cuando el dominio de diseño es completamente sólido.

La premisa de la metodología HCA es que un problema complejo en el espacio-tiempo puede discretizarse en una serie de reglas simples que operan sobre un gran número de autómatas dispuestos dentro de una rejilla uniforme y regular, los cuales sólo conocen condiciones locales.⁸ Dado que el dominio de diseño posee una forma arbitraria, la cual fue discretizada en una malla de elementos finitos, se realizó un mapeo de tal forma que cada elemento finito corresponda a un autómata celular, el cual estuvo determinado por la posición i que ocupa en la rejilla y por un conjunto de estados, que se define por una variable de diseño x_i y una variable de campo S_i.⁹

(7)

La elección de la variable de diseño en un problema de optimización topológica depende de la forma en que se modele el material del dominio de diseño. En esta investigación se empleó el enfoque de material sólido isotrópico con penalización SIMP,⁵ en el que cada autómata poseyó una densidad relativa x_i, que adquirió valores continuos en el intervalo [0,1], por lo tanto

(8)

Un autómata con densidad igual a cero no pertenece a la topología óptima, es decir, crea un agujero en el dominio de diseño, mientras que si la densidad relativa es igual a uno el autómata es sólido y por lo tanto hace parte del mecanismo diseñado. Dado que los valores intermedios son indeseables, pues no definen con claridad la topología óptima, las densidades relativas se penalizaron mediante un exponente p de tal forma que el módulo de elasticidad del autómata estuvo dado por

(9)

donde E₀ es el módulo de elasticidad del material en que se desea manufacturar el mecanismo.

Además de la restricción en los valores de la variable de diseño definida por la ecuación 8, en los problemas de optimización topológica es común definir la masa disponible para el diseño M_f como una fracción de la masa del dominio de diseño M_o,

(10)

donde f_m es la fracción de masa, cuyo valor está entre 0 y 1 y se define por el diseñador. Por lo tanto La masa final del mecanismo debe ser menor o igual a la masa disponible, de tal forma que

(11)

donde m_i es la masa del autómata celular sólido y N, el número de autómatas en la rejilla.

Al emplear las ecuaciones 5, 8, y 11 fue posible definir el problema de optimización topológica en forma estándar como

(12)

Estímulo mecánico y regla de evolución

Al aplicar la ecuación 12, el conjunto de estados para cada autómata se definió por la variable de diseño x_i y la variable de campo S_i, cuya selección dependió del problema de optimización a resolver. En esta investigación S_i se consideró como un estímulo mecánico que se determinó a partir de las condiciones de optimalidad de Karush-Kuhn-Tucker (KKT).⁸

A partir del problema definido por la ecuación 12, fue posible expresar su lagrangiano como

(13)

donde l es el multiplicador de Lagrange asociado a la restricción de masa y l_i2, l_i3 son los multiplicadores de Lagrange asociados a las restricciones en los valores de las densidades relativas x_i. Las condiciones KKT afirman que el valor óptimo de las variables de diseño se obtiene cuando la derivada parcial del lagrangiano respecto a éstas es cero,

(14)

de tal forma que fue posible reescribir la ecuación 14 a partir de la derivada parcial de la ecuación 13 y se obtuvo que

(15)

Para un autómata celular con densidad intermedia, i.e, 0 < x_i < 1, las restricciones en los valores de las variables de diseño no estuvieron activas, luego l_i2= l_{i3= 0} y la ecuación 15 fue satisfecha al ser

(16)

Entonces se definió la variable de campo S_i como

(17)

y su valor óptimo como

(18)

se pudo además demostrar que la ecuación 16 puede reescribirse como

(19)

Al ser la ecuación 19 la definición matemática del estado óptimo del autómata celular. En caso que éste no se alcance, una regla de evolución inspirada en la teoría de control de sistemas dinámicos modifica la variable de diseño con base en una señal de error e_i (t), que se define por la desviación entre el estímulo mecánico y su valor óptimo

(20)

de tal forma que la ecuación 19 se satisface cuando

(21)

Diversas reglas de control se reportan,⁹ sin embargo se conoce que la inspirada en el controlador proporcional-integral-derivativo (PID) es la que presenta mejores resultados, pues disminuye el número de iteraciones necesarias para la convergencia del algoritmo.⁸ La regla de evolución para este controlador se definió por la expresión

(22)

Al ser C_p la constante proporcional, C_I la constante integral y C_D la constante derivativa. Para alcanzar el estado óptimo, la densidad relativa del autómata evoluciona mediante la expresión

(23)

De tal forma que la convergencia del algoritmo se alcanzó cuando el cambio máximo de la variable de diseño entre dos iteraciones sucesivas fue menor a un valor de tolerancia a:

(24)

Implementación computacional

El algoritmo para diseñar mecanismos flexibles se desarrolló de acuerdo al diagrama de flujo ilustrado en la figura 2. Su implementación se realizó en MATLAB y constó de los siguientes pasos:

1) Definición el diseño inicial.

2) Realización del análisis estructural mediante el método de los elementos finitos para así evaluar MPE y SE en cada posición discreta i.

3) Cálculo del estímulo mecánico.

4) Estimación el valor del multiplicador de Lagrange l.

5) Cálculo de la señal de error, definido como

(25)

6) Aplicación de la regla de evolución para actualizar las densidades relativas.

7) Verificación de la restricción de volumen. Si esta se satisface, entonces, se puede continuar al paso 8, en caso contrario se debe volver al paso 4.

8) Verificación del criterio de convergencia: En caso que éste se solucione, el algoritmo termina y se obtiene el diseño final, en caso contrario se debe volver al paso 2.

RESULTADOS

Como ejemplo de la extensión de la metodología HCA a la síntesis topológica de mecanismos flexibles para aplicaciones biomédicas se propone el diseño de una micropinza para manipulación de fibroblastos. El objetivo de la síntesis topológica es obtener un cuerpo que permita generar una fuerza de apriete de 80 nN sobre una célula individual, lo cual corresponde a un desplazamiento de cierre de 18 mm de los puertos de salida, de acuerdo a datos experimentales.¹⁸ El material que se prefiere para la fabricación es un monocristal de silicón en forma de oblea polichada por ambas caras,¹⁹ con módulo de elasticidad E= 150 GPa y relación de Poisson n= 0.17. El dominio inicial tiene dimensiones de. 150 mm × 150 mm × 10 mm con un espacio entre pinzas de 50 mm × 30 mm, el cual permite prensar células individuales por su ancho. Para la obtención del mecanismo se decidió emplear únicamente el 50 por ciento de la masa del dominio inicial. La formulación matemática del problema de optimización para este diseño se definió como

(26)

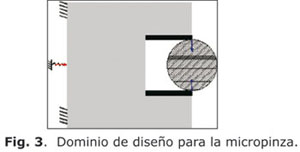
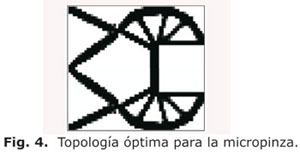
La configuración del dominio inicial, la posición de los soportes estructurales y los puertos de entrada y salida del mecanismo se ilustran en la figura 3, mientras que la figura 4 muestra la topología resultante luego de 25 iteraciones, la cual requiere una fuerza de activación de 40 nN.

CONCLUSIONES

Esta investigación propone la síntesis topológica de mecanismos flexibles para aplicaciones biomédicas, a través de un algoritmo de optimización topológica basado en la metodología HCA. Como ejemplo de esta extensión se realizó la síntesis de una micropinza para manipulación de fibroblastos. Los resultados evidenciaron la obtención de una topología sin juntas de facto o patrones de tablero de ajedrez, defectos que se presentan en otros algoritmos de optimización topológica. La ausencia de estos defectos posibilita la labor de postproceso del diseño, necesaria para realizar el proceso de manufactura.

Uno de los campos de trabajo futuro es el desarrollo de algoritmos que permitan realizar el postproceso de la topología, ya que el algoritmo entrega como resultado una imagen en mapa de bits. Para obtener un modelo CAD es necesario el análisis de imágenes digitales para vectorizar la imagen y poder parametrizar las fronteras del cuerpo con el empleo de curvas splines y nurbs, las cuales pueden dibujarse con un modelador de sólidos comercial. Otro campo de trabajo futuro es el diseño de las juntas flexibles que aparecen en la topología obtenida, pues el correcto dimensionamiento de éstas permite optimizar el desempeño del mecanismo y evitar la aparición de fallas por fatiga debido a la concentración de esfuerzos.

REFERENCIAS BIBLIOGRÁFICAS

1. Bashir R. BioMEMS: state-of-the-art in detection, opportunities and prospects. Advanced Drug Delivery Reviews. 2004;56:1565-86.

2. Erdman AG, Loftness PE. Synthesis of linkages for cataract surgery: storage, folding, and delivery of replacement intraocular lenses (IOLs). Mechanism and Machine Theory. 2005;40:337-51.

3. Ko WH. Trends and frontiers of MEMS. Sensors and Actuators A. 2007;136:62-7.

4. Howell L. Compliant Mechanisms. New York: Wiley Interscience, 2001.

5. BendsÆe MP, Sigmund O. Topology Optimization. 2. ed. Berlin: Springer Verlag, 2001.

6. Ananthasuresh GK, Kota S, Gianchandani Y. A methodical approach to the design of compliant micromechanisms. Solid-State Sensor and Actuator Workshop, 1994;189-92.

7. Pedersen CB, Buhl T, Sigmund O. Topology Synthesis of large-displacement compliant mechanisms. International Journal for numerical methods in engineering. 2001;50:2683-705.

8. Tovar A. Optimización topológica con la técnica de los autómatas celulares híbridos. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería. 2005;21(4).

9. Tovar A, Niebur GL, Sen M, Renaud J E. Topology optimization using a hybrid cellular automaton approach with distributed control. ASME Journal of Mechanical Design. 2006;128(6):1205-16.

10. Narváez CA, Tovar A, Bustos O. Tuned Proportional-Integral-Derivative Control for Topology Optimization using Hybrid Cellular Automata. Proceedings of the 7th World Congress on Structural and Multidisciplinary Optimization. Seúl, 2007.

11. Narváez CA, Tovar A, Garzón DA. Topology synthesis of compliant mechanisms using the hybrid cellular automaton method with an efficient mass control strategy. Proceedings of the III European Conference on Computational Mechanics. Lisboa, 2006.

12. Narváez CA, Tovar A, Galeano CH. Computer-Aided Topology Synthesis of compliant mechanisms with trajectory constraints. Proceedings of the 23rd ISPE International Conference on CAD/CAM, ROBOTICS & Factories of the Future - CARS & FOF 2007. Bogotá, 2007.

13. Zubir MNM, Shirinzadeh B. Development of a high precision flexure-based microgripper. Precision Engineering. 2009;33:362-70.

14. Zubir MNM, Shirinzadeh B, Tian Y. A new design of piezoelectric driven compliant-based microgripper for micromanipulation. Mechanism and Machine Theory. 2009;44:2248-64.

15. Kohl M, Krevet B, Just E. SMA microgripper system. Sensors and Actuators A. 2002;97-98:646-52.

16. Nah SK, Zhong ZW. A microgripper using piezoelectric actuation for micro-object manipulation. Sensors and Actuators A. 2007;133:218-24.

17. Tian Y, Shirinzadeh B, Zhang D. A flexure-based five-bar mechanism for micro/nano manipulation. Sensors and Actuators A. 2009;153:96-104.

18. Yang S, Saif T. Reversible and repeatable linear local cell force response under large stretches. Experimental Cell Research. 2005;305:42-50.

19. Kotzar G, Freas M, Abel P, Fleischman A, Roy S, Zorman C, Moran J M, Melzak J. Evaluation of MEMS materials of construction for implantable medical devices. Biomaterials. 2002;23:2737-50.

Recibido: 12 de noviembre de 2009.
Aprobado: 20 de diciembre de 2009.

Carlos Alberto Narváez. Departamento de Ingeniería Mecánica y Mecatrónica, Universidad Nacional de Colombia. E mail: [e-mail]