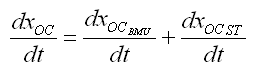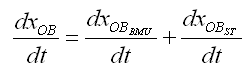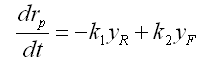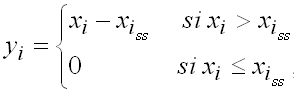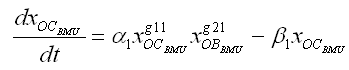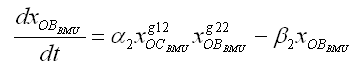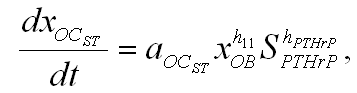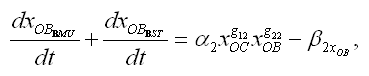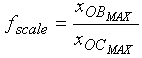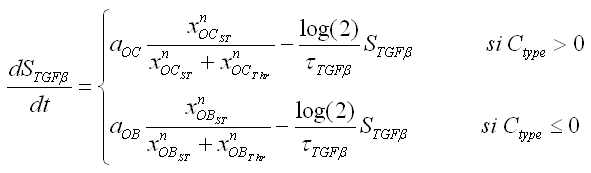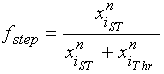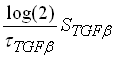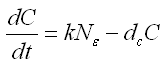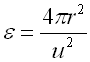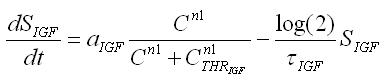ARTÍCULOS ORIGINALES

 

Descripción de la metástasis del cáncer en el tejido óseo a través de un modelo matemático

 

Description of cancer metastasis in bone tissue through a mathematical model

 

 

Diego Alexander Garzón-Alvarado^I; Angélica María Ramírez Martínez^II; Octavio Silva^III

^IDoctor en Ciencias (PhD), Máster en Ciencias, Ingeniero Mecánico. Profesor Adjunto. Facultad de Ingeniería. Universidad Nacional de Colombia, Bogotá.
^IIProfesora de Ingeniería Mecánica. Facultad de Ingeniería. Fundación Universidad Central, Bogotá-Colombia.
^IIIProfesor de Medicina Física. Facultad de Medicina. Universidad Nacional de Colombia, Bogotá.

---

RESUMEN

La metástasis es la rápida proliferación de células de cáncer, tumor secundario, en un sitio específico, que, en general, conduce a la muerte. Este proceso ocurre en sitios anatómicos que proveen el ambiente necesario de vascularización, oxígeno y alimento que le permiten camuflar su acción para desencadenar el rápido crecimiento del cáncer. El cáncer de próstata y de mama utiliza, por ejemplo, la médula ósea para su proliferación. Por lo tanto, el hueso da soporte para que las células de cáncer se adapten al ambiente, imiten el comportamiento genético y molecular de las células óseas. En este trabajo se simula el proceso de metástasis del cáncer con activación de la medula ósea. Para ello se plantea un modelo matemático que involucra la activación molecular, por parte de las células del tejido óseo, necesaria para la proliferación del cáncer. En este orden de ideas se simula dos posibles formas de crecimiento del tumor secundario según el tipo de metástasis: la osteoclerosis y la osteolisis.

Palabras clave: cáncer, metástasis, mecanismos moleculares, médula ósea.

---

ABSTRACT

Metastasis is the fast proliferation of cancer cells, secondary tumor in a specific site, that in general lead to death. This process occur in anatomical sites providing the necessary environment of vascularization, oxygen and food allowing to camouflage its action for triggering the fast growing of cancer. Prostrate and breast cancer use by example, the bone marrow for its proliferation. Thus, the bone gives support for the adjustment cells to environment; mimic the genetic and molecular behavior of bone cells. In present paper the cancer metastasis process is simulated with bone marrow activation. Authors propose a mathematical model involving the molecular activation by the bone tissue cells, needed for cancer proliferation. In this order of ideas two ways of secondary tumor growth is simulated according the type of metastasis: The osteosclerosis and osteolysis.

Key words: Cancer, metastasis, molecular mechanisms, bone marrow.

---

 

 

INTRODUCCIÓN

Una de las enfermedades más letales del mundo contemporáneo es el cáncer según la Sociedad Americana de Cáncer,^1,2 para el año 2008, en Estados Unidos, se esperaba que el número de nuevos casos que se diagnosticaran fuera de 1 437 180 y el número de decesos de 565 650. Por ejemplo, en el caso de los hispanos en Norteamérica los recuentos ubican al cáncer como la tercera causa de mortalidad, después de enfermedades combinadas y aquellas relacionadas con el corazón.² Entre los diferentes tipos de cáncer, las estadísticas muestran que los más lesivos a la población masculina es el cáncer de próstata y, en las mujeres, el cáncer de mama.^2,3,4 En esta misma lista se ubican el cáncer de pulmón y bronquios y el de colon y recto que afectan de manera indiferente a los dos géneros.²

El cáncer se entiende como una enfermedad celular. Las células que inicialmente son normales se alteran de tal manera que pierden sus características y desarrollan un nuevo comportamiento acompañado de cambios de apariencia celular, membrana y crecimiento. Es así como estas células pueden reemplazar otras y asumir sus funciones que le ayudan a mimetizarse en el entorno de un órgano o tejido. Luego de su progresión primaria, estas células pueden migrar a un lugar remoto, acción que se denomina metástasis.⁵

La causa de muerte de la mayoría de pacientes con cáncer es el desarrollo de la metástasis en sitios lejanos al tumor primario.^6,7 La metástasis se describe como el proceso por el cual se difunden las células malignas y se desarrolla el cáncer secundario en sitios diferentes al original. Mendoza y Khanna⁶ describen como las células cancerígenas atraviesan la membrana basal del tumor y alcanzan la circulación sanguínea que sirve de transporte a otras partes del organismo en donde se lleva a cabo el desarrollo del cáncer secundario. En aquel sitio distante, estas células deben salir del torrente sanguíneo para sobrevivir al nuevo microambiente, proliferar, inducir angiogénesis y crecer satisfactoriamente en una lesión metastásica.⁷ Es precisamente en el hueso donde ocurre el proceso de metástasis del cáncer.

El hueso es el segundo sitio anatómico donde se desarrolla el cáncer, gracias a la metástasis cancerígena en la medula ósea. Principalmente el cáncer de próstata y de mama produce el 70 % de metástasis esqueléticas. Cecchini y cols.¹ argumenta como el crecimiento de células de cáncer se da de manera activa durante la reabsorción ósea. Este proceso desencadena efectos moleculares y genéticos que pueden producir complicaciones óseas severas como son: las fracturas, compresión de la medula espinal y aplasia medular,⁸ reemplazo de medula ósea roja por amarilla. En modelos experimentales, en animales, se reporta que existe un elevado número de células^1,8 de tumor que pueden alcanzar el torrente sanguíneo, pero una pequeña fracción de estas son capaces de desarrollar metástasis.^8,9 Una que vez las células se encuentran en su tejido objetivo, estas sobreviven al microambiente óseo gracias a que se establece una afinidad única que le permite crecer.

Von Recklinghausen,¹ hace más de un siglo, determinó que la colonización y el crecimiento de cáncer ocurre en la médula ósea. Es así como la metástasis se presenta de forma común en el esqueleto axial más que en el apendicular. Batson¹⁰ y Frandks¹¹ demostraron que existen redes para vertebrales de venas de pared delgada que son importantes en el desarrollo de la metástasis en el hueso, gracias a su localización y disminución de flujo sanguíneo, lo que le permite a las células cancerígenas llegar a su destino. También se ha determinado que la afinidad y distribución de estas células pueden estar en relación con la actividad hematopoyética de la medula ósea roja.¹²

Dos mecanismos de metástasis se presentan en el hueso, el primero es la osteolítica, en donde las células del tumor tienen la habilidad de reabsorber el hueso, de tal manera que los osteoclastos son requeridos para la osteolisis y para el crecimiento del tumor. Este mecanismo puede llevar al hueso a la fractura gracias a su continua disminución de masa ósea por la reabsorción.¹³ El otro gran mecanismo es la osteoclerosis, que es la exagerada respuesta osteoblástica, por lo que se presenta un incremento desmedido de la matriz mineralizada generando huesos de gran masa y posibilidades de fractura y falta de irrigación sanguínea por compresión.¹

Sobre estos tipos de metástasis se han realizado diversos experimentos para encontrar la solución para quienes la padecen. Por ejemplo, entre los más recientes se cuenta a Hirbe y cols.¹⁴ donde se muestra la acción de biofosfonatos sobre la actividad osteoclástica que inhibe la reproducción celular cancerígena. Ebert y cols.¹⁵ muestran el efecto del ácido zoledrónico sobre la actividad de diferenciación osteoclástica como tratamiento efectivo para la metástasis. Sin embargo otros artículos ponen en duda la eficacia de estos tratamientos y discuten el papel de otros productos farmacéuticos como el clodranato, pamidronato e ibandronato, los cuales producen variaciones en el diagnóstico de la metástasis.¹⁶ Gracias a la continua discusión sobre el proceso del cáncer en equipos interdisciplinarios compuestos por matemáticos e ingenieros, biólogos, médicos, químicos, entre otros, se generan modelos precisos que expliquen el discurrir de la enfermedad desde la óptica de los fenómenos físicos y biológicos con el ánimo de cuantificar los efectos de cada factor que interviene en la enfermedad. Modelos como el de Freedman y Pinho,¹⁷ Zhou y Cui,¹⁸ quienes refieren también a Bianchi y Fasano, entre otros, muestran la acción de los nutrientes, proteínas y el problema de estabilidad matemática en los procesos de crecimiento del tumor maligno.

En este artículo se desarrolla un modelo de metástasis de cáncer en el tejido óseo con el objeto de describir la dinámica celular y de evolución molecular de los factores más relevantes en el proceso de crecimiento del tumor secundario. Para ello se plantearon ecuaciones diferenciales para la diferenciación celular y cada uno de los factores que emiten. A partir del sistema de ecuaciones acopladas se lleva a cabo la solución mediante métodos numéricos. Por tanto, el artículo está dividido en 4 secciones. En la primera, se desarrolla la teoría sobre la metástasis en un hueso y se describe su relación con el proceso de remodelación ósea. Posteriormente se plantea el modelo a solucionar, para el que se muestran los resultados del mismo. Por último se lleva a cabo la discusión sobre el modelo y los resultados obtenidos.

MÉTODOS

Metástasis en el hueso

El tumor secundario crece en la cavidad medular y se favorece con el proceso de remodelación ósea. El grado relativo de reabsorción o deposición de hueso es altamente variable y depende del tipo y localización del tumor. Esta relación entre los osteoclastos y osteoblastos, durante el proceso de remodelación, determina la osteoesclerosis, la osteolisis o patrones combinados que se puede apreciar en radiografías.^19,20

El proceso de crecimiento del tumor se encuentra en relación con la actividad hematopoyética de la cavidad medular roja del hueso.¹² En este sitio, las células pueden sobrevivir gracias al ambiente favorable que presenta el hueso durante el proceso de remodelación. Los eventos previos de la metástasis se inician en el tumor primario, donde células de éste se desprenden y entran al sistema linfático o sanguíneo para formar agregados que están en interacción con los leucocitos y plaquetas. Las células sanguíneas le permiten pasar a través de capilares de órganos, resistir a los esfuerzos cortantes y protegerse del sistema inmune.²¹ En esta lucha por la supervivencia, las células cancerígenas interactúan con el endotelio para extravasar las células tumorales y hospedarse en un tejido específico. Es así como las células se adhieren principalmente al hueso gracias a moléculas de adhesión y quimioatractantes que retienen estas células en los sitios de vascularización del hueso.

Una vez que las células de cáncer están en un tejido específico, se lleva a cabo la eventual proliferación del tumor.²² Específicamente, durante la fase de reabsorción y formación, el microambiente del hueso contribuye a la metástasis a través de la liberación y activación de factores que permiten el crecimiento tumoral. Por tal motivo, en esta sección se desarrolla la relación que existe entre la remodelación ósea y la metástasis. Para ello se describe inicialmente el proceso de remodelación y a partir de este se referencia la metástasis, desde la perspectiva molecular y celular.

Remodelación ósea

Se denomina remodelación ósea al proceso por el cual se renueva la matriz mineralizada de hueso. En este proceso se pueden distinguir tres fases: reabsorción, reposo y formación.²³ La fase de reabsorción se inicia con la diferenciación de un grupo de osteoclastos a partir de sus precursores. Estos osteoclastos erosionan o reabsorben matriz ósea en formas cónicas denominadas lagunas de Howship. Esta fase termina con la eliminación de los osteoclastos por apoptosis.²⁴ La fase de reposo o inversión tiene lugar cuando se completa la reabsorción osteoclástica, y aparecen células mononucleares en la superficie ósea, los preosteoblastos. Estas células preparan la superficie para la formación de nuevo tejido óseo y proveen señales para la diferenciación y migración de osteoblastos.²³ Por último, la fase de formación se inicia con la diferenciación de un grupo de osteoblastos a partir de los preosteoblastos, y en ella los osteoblastos segregan matriz ósea nueva que rellena las zonas excavadas. Es de resaltar que los osteoblastos derivan de células madre mesenquimales, y los osteoclastos son el resultado de la diferenciación de sus precursores a partir de progenitores hematopoyéticos y su posterior evolución hasta osteoclastos maduros multinucleados, o sea osteoclastogénesis.²⁵ Cada una de estas células se encarga de cumplir el ciclo de remodelación. El proceso de deposición de nueva matriz dura unos 10 a 20 días, con lo cual termina el ciclo de remodelación.²⁴

Las tres fases descritas anteriormente, que constituyen el proceso de remodelación, son ejecutadas en un sitio específico por un bloque celular que se denomina unidad multicelular básica (BMU).²⁶ Una BMU es un conjunto de células que intervienen en un punto específico para realizar un ciclo de remodelación ósea, compuesto principalmente por osteoclastos y osteoblastos. Es de señalar que en un instante dado existen muchas BMUs que actuan en diferentes lugares y su acción se presenta en diferentes fases.

La tasa de intercambio en el volumen total de hueso antiguo por hueso nuevo por unidad de tiempo, se denomina recambio óseo.^23,26 Es decir, que el recambio óseo es proporcional a la cantidad de ciclos de remodelación en actividad. Además, el trabajo y la organización de la BMU difiere morfológicamente entre hueso cortical y trabecular. En el hueso cortical las BMUs forman un canal cilíndrico de unos 2 mm de longitud por un diámetro entre 150 a 200 mm, avanzando a través del hueso a una velocidad de 20 a 40 mm/día.

Este proceso de remodelación ósea se controla por un conjunto de factores externos o sistémicos e internos o locales.^23,26 Los factores sistémicos de mayor relevancia son la acción de la hormona paratiroidea (PTH) y la vitamina D, además de las hormonas tiroideas, esteroides sexuales, glucocorticoides, insulina y la hormona del crecimiento. La acción puede ser directa sobre las células óseas o sobre algunos factores locales.

El número de BMUs que se encuentran en el proceso de destrucción y formación dependen, también de otros factores, como son: la cargas mecánicas, citoquinas y hormonas.²⁸ Es así como las células del linaje osteoblástico inducen el reclutamiento de osteoclastos en el sitio donde se llevará a cabo la reabsorción.²⁹ Los osteoblastos expresan: factor-1 estimulante de colonias (en inglés: colony stimulating Factor-1, CSF-1) y receptor-activador del factor ligando nuclear (en inglés: Receptor activator for nuclear factor ligand, RANKL), quien también se conoce como factor de necrosis tumoral dependiente de la activación inducida por citoquinas (en inglés: TNF-related activation-induced cytokine, TRANCE), factor de diferenciación osteoclástica (en inglés: osteoclast differentiation factor, ODF), el cual, como su nombre lo indica, actúa sobre el RANK (ubicado en la superficie) de los preosteoclastos para que se diferencien en osteoclastos e inicien el proceso de reabsorción.¹ En contraposición, la osteoprotegerina (OPG) sirve como anzuelo del RANKL (OPGL) de tal forma que inhibe su acción sobre los preosteoclastos. Otros tipos de moléculas como la hormona paratorioidea (PTH) y la hormona paratiroidea péptida relacionada (PTHrP) aumentan RANKL y disminuyen la expresión de OPG por los osteoblastos.¹ También la vitamina D3, estrógenos (E) y citoquinas como la interleukina (IL-6, IL-11 y IL-18) actúan sobre la generación de osteoclastos, gracias a la regulación del RANKL por acción sobre los osteoblastos.^29,30 De la misma forma, existen moléculas que se generan por el osteoblasto y que ayudan a su propia diferenciación como es el factor-1 de crecimiento tipo insulina (en inglés: insulin-like growth factor-1, IGF) y el factor transformador de crecimiento-beta (en inglés: transforming growth factor, TGF-b), este último se libera por el osteoclasto y colabora en su diferenciación y en la del preosteoblasto,^31,32 (Fig. 1).

Por tanto, se puede concluir que el proceso de remodelación ósea tiene una dinámica compleja en el que interviene factores moleculares, directos o indirectos que actúan sobre las células de la BMU y estas, a su vez, expresan moléculas que activan o inhiben la diferenciación, apoptosis y direccionan el comportamiento celular. En la tabla 1 se muestran los principales factores involucrados en el proceso de remodelación ósea.

Metástasis de cáncer en el hueso

Gracias al proceso de reabsorción y formación ósea, en el hueso se pueden presentar dos casos de metástasis: osteolisis y osteoclerosis.¹ La osteolisis presenta una disminución excesiva de masa ósea como resultado del aumento de los osteoclastos, por parte de factores moleculares liberados por el tumor, que son los encargados de la reabsorción de hueso. En la osteoclerosis se presenta el efecto contrario, es decir, un aumento excesivo de hueso gracias a que el tumor secundario activa la diferenciación de osteoblastos, encargados de la formación de hueso. En los siguientes apartados se mostrará cada caso y los factores moleculares involucrados en la metástasis.

Caso osteolisis

En el caso de la osteolisis, se presenta un ciclo vicioso en el microambiente que permite el crecimiento del tumor.¹ Cecchini y cols.¹ describen el crecimiento del tumor secundario gracias a la inclusión en el microambiente del hueso de las células cancerígenas. Estas últimas liberan múltiples factores moleculares que alteran el funcionamiento de las BMUs que se encargan de formar y destruir el hueso. Se ha encontrado^33,1 que el tumor libera hormona paratiroidea péptida relacionada (PTHrP), que forma parte de la familia de hormonas tiroideas y que acciona en los osteoblastos la liberación excesiva del RANKL y la disminución de OPG. Gracias a la liberación del ligando (RANKL) se inicia el proceso de diferenciación de los preosteoclastos presentes en la línea hematopoyética para convertirse en osteoclastos responsables de reabsorber el hueso. A su vez, los osteoclastos liberan factor de crecimiento tumoral beta (en inglés: Tumor Growth Factor b, TGFb) que activa la mitosis de las células cancerígenas. Este proceso se genera gracias a que, el tumor secundario se alimenta activamente del microambiente óseo. Por ello se forma un ciclo vicioso.

Caso Osteoclerosis

La osteoclerosis es un proceso aún poco entendido.¹ En el proceso de formación de la metástasis en el hueso, se genera un incremento apreciable de la masa ósea gracias al aumento del número de osteoblastos presentes en la remodelación. Aunque no se conoce exactamente el factor que incide en el aumento del número de células del tumor, se cree que es un efecto combinado de hormonas paracrinas que aún no está bien determinado. Estas hormonas activan la diferenciación de células del tumor, y este, a su vez, libera: TGF, IGF, proteínas morfogénicas óseas (BMP), entre otras, que aumentan la cantidad de osteoblastos, de esta forma aumenta la cantidad de masa ósea, lo que produce huesos más pesados y genera compresión de venas y arterias que lo irrigan.

Luego de analizar los procesos de metástasis, se diseñó el modelo matemático que describe el proceso de crecimiento del tumor secundario.

Modelo matemático de la metástasis en hueso

Modelo matemático de remodelamiento óseo

Durante los últimos años se incrementó el estudio de la influencia de los diversos factores en el proceso de remodelación ósea, ya que de su conocimiento depende el desarrollo de terapias y tratamientos para enfermedades tales como la enfermedad de Paget, la osteoporosis y la metástasis de hueso, entre otras. Muchos son los modelos que se reportan para abstraer el funcionamiento general del proceso de remodelación y la interacción de los diversos factores, algunos modelos enfatizan el nivel sistémico, otros el nivel celular y otros en el nivel molecular.^34-38

Frost,³⁹ en 1987, planteó un sistema de retroalimentación negativa para explicar cómo los esfuerzos que actúan en los huesos determinan su forma, esta es la base de los modelos mecanostáticos de formación ósea. Kroll,⁴⁰ en 2000, describió un modelo de poblaciones de osteoblastos y osteoclastos con enfoque en la respuesta ante la administración de PTH. Komarova y Cols.,³⁴ en 2003, desarrollaron un modelo celular del ciclo de remodelación ósea según las relaciones autocrinas y paracrinas. Lemaire y Cols., ³⁵ en 2004, profundizaron en su modelo las influencias concretas de factores como RANKL y OPG en la dinámica de remodelación ósea. Moroz y Cols.,³⁶ en 2006, plantean un modelo celular basado en la cinética de las poblaciones descrita por Michaelis-Menten en 1913, también empleadas por otros autores.^37,38

En este trabajo, el modelo de remodelación de hueso, a nivel celular y bajo la influencia de factores moleculares locales se basa en el siguiente conjunto de ecuaciones:

(1a)

(1b)

(1c)

donde: x_OC y x_OB son el número de osteoclastos y osteoblastos presentes durante el proceso de remodelación y que dependen del número de células a nivel de la BMU normal (x_OCBMU y x_OBBMU) más el número de células que se generan gracias al proceso de osteolisis u osteoclerosis por el tumor secundario (x_OCCST y x_OBST). Además, y_R y y_F están dados por:

(1d)

Para la dinámica de la BMU normal se utilizó el modelo de por Komarova,³⁴ en donde se un conjunto de ecuaciones diferenciales modelan el comportamiento de las poblaciones de osteoclastos y osteoblastos en una unidad multicelular ósea (BMU), en relación con factores autocrinos y paracrinos locales. En este modelo el ciclo de remodelación se inicia cuando los osteoclastos se diferencian a partir de los preosteoclastos para obtener un aumento en la población. Estos osteoclastos inician la reabsorción de hueso con la consecuente pérdida de masa ósea. Sin embargo, este evento a su vez induce la diferenciación de osteoblastos con la consecuente formación y restitución de masa ósea. Por tanto, las ecuaciones para la BMU normal están dadas por:

(2a)

(2b)

donde: x_OCBMU y x_OBBMU son el número de osteoclastos y osteoblastos que participan en la BMU bajo condiciones normales, a_i y b_i son valores de acción sobre el proceso de formación de hueso y reabsorción, r_p es el porcentaje de masa ósea en cada instante del tiempo, k₁ y k₂ son los valores de efectividad de reabsorción y formación de huesos, respectivamente; x_OCSS y x_OBSS son los valores de estado estable del sistema dinámico (2). Los g_ij, son los valores que representan la efectividad de los factores autocrinos y paracrinos que actúan sobre las células, de tal forma que, por ejemplo, g₁₁ describe la acción de los factores autocrinos que se expresan por los osteoclastos y tienen como objetivo los mismos osteoclastos, g₂₁ son los factores paracrinos que se expresan por los osteoblastos y actúan sobre la diferenciación de osteoclastos.

Por su parte, en presencia de un tumor secundario, puede existir un aumento de osteoblastos (exceso de masa ósea, caso osteoclerosis) o un aumento de osteoclastos (exceso de reabsorción ósea, caso osteolisis). En el caso de un aumento del número de osteoclastos, se supone que la función (3) depende del número de osteoblastos que generan un aumento de RANKL y una disminución de OPG, gracias al estimulo que, sobre estos, genera el tumor secundario a través del PTHrP por lo que se supone:

(3)

donde: a_OCST, h₁₁ y h_PTHrP son constantes que establecen la tasa y efectividad de diferenciación de osteoclastos, efectividad de expresión de RANKL a partir de los osteoblastos y efectividad de la acción del PTHrP sobre los osteoblastos para permitir su diferenciación; S_PTHrP es la concentración de PTHrP que se expresa gracias al tumor secundario.

Además, el aumento del número de osteoblastos depende del mismo número de osteoblastos (y osteoclastos) que se diferencian gracias a la acción que las células del tumor secundario ejercen a través de la expresión de IGF. Por tanto, con un argumento similar al de la BMU normal se tiene que:

(4a)

donde: g₂₂(S_IGF) está dado por

(4b)

donde: g_22BMUN es una constante de efectividad de los factores autocrinos para la formación de osteoblastos, es el factor de perturbación de osteoblastos para su propia diferenciación gracias a la expresión de IGF por parte del tumor secundario y S_IGF es la concentración de IGF regulada por el tumor.

Modelo matemático de la producción de TGF-b (Factor de crecimiento de tumor b)

El crecimiento del tumor secundario depende de las sustancias moleculares que libera los osteoblastos u osteoclastos según sea el caso de metástasis ósea: osteolisis u osteoclerosis. Para ello, se supone inicialmente que existe un proceso de decisión que depende del número de células presentes durante el proceso de remodelación y depende, también, de un proceso aleatorio que incluye efectos del metabolismo, predisposición y genética del individuo, esto es:

(5)

donde: f_scale es un factor que mantiene en la misma escala al número de osteoclastos y osteoblastos, esto se debe a que el número de osteoclastos presentes en el proceso de remodelación es mucho menor al número de osteoblastos de la BMU,³⁴ es decir,

(5a)

donde: los subíndices indican valores máximos de osteoblastos y Osteoclastos en una BMU normal. Por su parte, RN es un número aleatorio del intervalo (-x_OBMAX= RN= x_OBMAX). Por tanto, el desarrollo del tipo de cáncer depende del instante en que se instaure el tumor secundario, si la BMU se encuentra en reabsorción o formación, y también del tipo de metabolismo y factores diversos, que representa el número aleatorio.

Entonces, una vez descrito el tipo de metástasis que se presentará en el hueso, el proceso de crecimiento del tumor secundario depende de la expresión molecular de las células óseas, esto es:

(6)

donde: a_OC y a_OB son constantes de producción de TGFb por parte de las células osteoclastos y osteoblastos, respectivamente;

es la función escalón para el cual se inicia el proceso de liberación de TGFb por parte de cada célula (i= OC, OB), n es el valor que mide la pendiente de la función y xn es el valor umbral del número de células para el cual se inicia el proceso de liberación de TGFb, ver figura 2.^41,42 El segundo término:

hace referencia al proceso de desaparición del T GF b debido al tiempo de vida promedio T_TGFb (ver tabla 1).

Modelo de crecimiento del tumor secundario (metástasis)

Al tener como referencia el modelo de crecimiento de cáncer de Piotrowska y Angus,⁴⁴ se consideró que se instaura un número mínimo de células tumorales (N) en el hueso para iniciar el proceso de metástasis. El tamaño de este tumor inicial esta dado por:

(6c)

donde: u es el tamaño del cubo equivalente que tiene el mínimo número de células, ñ es la densidad del tumor, en unidades de células por cm³ y r es el radio del tumor inicial. A partir de este dato se desarrolló una ecuación que determinó el crecimiento del tumor dado por (7) y que tuvo en cuenta la activación por parte del TGFb, la geometría y las condiciones mínimas de crecimiento y la muerte celular:

(7)

donde: C es el número de células que se encuentran en el tumor, N es el número de células mínimo para el crecimiento y d_c es el número de células tumorales que mueren por apoptosis o desaparecen por diferentes procesos, como migración, por ejemplo. Por su parte, k es el factor de crecimiento y e el factor de geometría del tumor, que están dados por:

(8a)

(8b)

donde: r es la tasa de mitosis celular debido a la presencia de TGFb en el microambiente del tumor, S_{THR TGFb} es el valor umbral necesario para iniciar el proceso de crecimiento del tumor y n_t es la pendiente de la función escalón. Por otro lado, la ecuación para e se refiere a la geometría de crecimiento, esto significa la cantidad de paquetes de células con N número de células que están en la superficie del tumor y que están habilitadas o activas para llevar a cabo el proceso de mitosis, ver figura 3. Gracias al crecimiento del tumor, el radio del tumor, del término e que evoluciona en el tiempo mediante la ecuación:

(9)

Modelo de expresión de PTHrP (Caso osteolisis) y expresión de IGF (Caso osteoclerosis)

En el caso de la osteolisis, se reporta que las células de cáncer liberan la molécula hormona paratiroidea péptida relacionada (PTHrP) que activa, en los osteoblastos, la expresión de RANKL y la disminución de OPG.¹ Es así como se inicia el ciclo vicioso que antes referimos. Suponemos que PTHrP es función únicamente de la cantidad de células tumorales presentes en el sitio de metástasis, esto es:

(10)

donde: a_PTHrP es la tasa de liberación de PTHrP por parte de las células cancerígenas, C_THRPTHrP es el número de células umbral en el cual se inicia la liberación de PTHrP por parte del tumor, nP es el valor de la pendiente de la función de activación referida en la figura 2 y t _PTHrP es el valor del tiempo promedio de vida de la molécula.

De igual manera, y para el caso de la osteoclerosis, se registra que las células cancerígenas liberan factores moleculares que aumentan la diferenciación de osteoblastos, lo que a su vez, genera una excesiva formación de hueso. En este caso la molécula que se libera no está bien descrita y se desconoce del proceso de la osteoclerosis.¹ Por ello suponemos que la molécula liberada es el factor de crecimiento insulínico, (IGF),¹ la cual se modela como:

(11)

donde: a_IGF es la tasa de liberación de IGF por parte de las células cancerígenas, C_THRIGF es el número de células umbral en el cual se inicia la liberación de IGF por parte del tumor, nI es el valor de la pendiente de la función de activación referida en la figura 2 y t _IGF es el valor del tiempo promedio de vida de la molécula.

De esta forma se obtuvo el conjunto de ecuaciones que rigen el comportamiento del crecimiento de un tumor secundario en metástasis. El modelo matemático se debe solucionar numéricamente, por tal razón se hacen ensayos computacionales con el objetivo de obtener el conjunto de parámetros del modelo y hallar soluciones factibles desde el punto de vista biológico. En la siguiente sección se muestra el algoritmo en la solución del modelo.

Implementación numérica del modelo

El conjunto de ecuaciones acopladas descritas en párrafos anteriores se solucionaron con el uso de un método de Runge-Kutta de cuarto orden según Hoffman.⁴⁵ La solución se realizó en Fortran y se ejecutó en un computador portátil con procesador Intel Core 2 Duo de 2G de Ram y 1,58GHz de velocidad. El algoritmo que se siguió en la solución se ve en la figura 4.

Por su parte, las constantes se hallaron mediante pruebas numéricas y por la literatura referente al tema. En la tabla 2 se expone el rango, las unidades y el valor de cada constante del modelo.

En la simulación se utilizó como condiciones iniciales un valor de 10,9 osteoclastos, 231 724 osteoblastos y un 95,5 % de masa ósea. Para simular la instauración del tumor secundario se tomaron como valores iniciales 400 células en el tiempo t= 600 días. El tamaño del paso en la iteración de Runge-Kutta fue de 0,1 días y el cálculo requirió un tiempo promedio de 5 minutos.

RESULTADOS

En las figuras 5, 6 y 7 se muestran los resultados del número de osteoblastos, osteoclastos y de masa durante el proceso normal de remodelación ósea en 2 600 días. En este caso no se instauró ningún tumor, por tanto la BMU tuvo un funcionamiento normal, de tal forma que, el número de osteoblastos y osteoclastos que se presentan en cada ciclo de remodelación es el adecuado para mantener la masa del hueso, por lo que, simplemente, se realiza un recambio de tejido.

Caso de instauración del tumor con osteolisis

En este caso se instauró un tumor secundario en el día 600, sin embargo gracias al ciclo vicioso que explicamos en párrafos anteriores se presentó un aumento dramático del tamaño del tumor hasta el día 1 500. Se observó que el número de osteoblastos (Fig. 8) fue similar a la evolución normal de las mismas células, sin embargo, el número de osteoclastos (Fig. 9) creció considerablemente a partir de la evolución del tumor. Gracias a que el número de osteoclastos aumentó y los osteoblastos se mantuvieron en un número bajo comparativamente existió una disminución progresiva de la masa ósea (Fig. 10).

Obsérvese que al aumentar el número de osteoclastos aumentó la producción de TGFâ, gracias a esta molécula aumentó el tamaño del tumor en radio y en número de células, ver figuras 11, 12 y 13. Este aumento progresivo del tumor secundario incrementó, a su vez, la producción de PTHrP (Fig. 14), que causó la diferenciación de preosteoclastos.

Caso de instauración del tumor con osteoclerosis

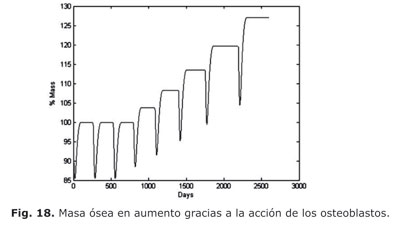
En este caso, se observó que el número de osteoclastos se mantuvo aproximadamente similar al caso normal y el número de osteoblastos creció constantemente en el tiempo, ver figuras 15 y 16, por tal razón se produjo una alta cantidad de TGFâ que aumentó el crecimiento del tumor. El tumor, por su parte, creció exponencialmente y liberó IGF, ver figuras 17, 18, 19 y 20, lo que aumentó el número de osteoblastos presentes en el proceso de remodelación anormal.

Los resultados, producto de la simulación, se encontraron en un rango biológicamente aceptable según otros autores.^46,47 Se observó que la evolución de un tumor secundario pudo darse en un intervalo entre 8 a 86 meses antes de producirse el deceso.⁴⁶ A su vez, el diámetro de los tumores coincidió con valores encontrados en la literatura referente al tema,⁴⁷ donde el diámetro pudo variar entre unos cuantos milímetros hasta 2 centímetros. Sin embargo, los niveles de concentración de los factores moleculares que estimulan el crecimiento del tumor, los niveles autocrinos y paracrinos de los factores secretados por las células óseas no fueron medidos en el tiempo.

CONCLUSIONES

En este artículo se presentó un modelo matemático sobre la metástasis del cáncer en el hueso. Se logró diseñar un modelo que contiene información sobre la relación de las moléculas autocrinas y paracrinas con la proliferación de las diferentes células de que se compone el proceso de metástasis del cáncer (tumor secundario). El modelo fue resuelto a través de Runge-Kutta de cuarto orden y mostró la versatilidad del método numérico para diferentes sistemas acoplados.

Los resultados, producto de la simulación, se encontraron en un rango biológicamente aceptable. Los niveles de concentración de los factores moleculares que estimulan el crecimiento del tumor, los niveles autocrinos y paracrinos de los factores secretados por las células óseas no fueron medidos en el tiempo, por ello el resultado del modelo propuesto, es una aproximación a la realidad y se convierte en un primer acercamiento al modelado de la metástasis.

Por ser una aproximación es importante hacer notar las carencias del modelo. En primera instancia se reconoce que los parámetros del modelo son desconocidos y se hallan a partir de experimentación numérica, lo cual, puede diferir de la realidad. En segundo lugar, el modelo representa un punto en el espacio, lo cual es una suposición incompleta. Un tumor secundario crece a expensas del aporte de nutrientes y factores de proliferación que provienen de múltiples sitios del hueso; existe una participación de varias BMUs en diferentes instantes de tiempo, lo cual no se tuvo en cuenta en el modelo. En tercer lugar, la ubicación del tumor exhibe diferencias ostensibles en la geometría y en la proliferación de las células cancerígenas.

A pesar de las limitaciones antes enunciadas, el modelo matemático antes descrito permite aproximar, de manera cualitativa, la evolución de un tumor secundario. Este modelo deberá ampliarse y extenderse a varias dimensiones espaciales para predecir la fractura y el crecimiento de un tumor en huesos específicos del cuerpo.

REFERENCIAS BIBLIOGRÁFICAS

1. Cecchini MG, Wetterwalda A, Van der Pluijmb G, Thalmanna G. Molecular and Biological Mechanisms of Bone Metastasis. EAU Update Series. 2005;3:214-26.

2. American Cancer Society. Cancer Facts and Figures 2008. American Cancer Society. USA: Atlanta. 2008.

3. American Cancer Society. Cancer Facts and Figures 2007. American Cancer Society. USA: Atlanta. 2008.

4. American Cancer Society. Cancer Facts and Figures 2006. American Cancer Society. USA: Atlanta. 2008.

5. Varricchio CG, editor. A cancer Source Book for Nurses. 8. ed. Atlanta: Jones and Bartlett Publishers, Inc.; 1997:550.

6. Mendoza M, Khanna C. Revisting the seed and soil in cancer metastasis. The International Journal of Biochemistry and Cell Biology, 2009;41:1452-62.

7. Steeg PS, Theodorescu D. Metastasis: A therapeutic target to cancer. Nat Clin Pract Oncol. 2008;5:206-19.

8. Butler TP, Gullino PM. Quantitation of cell shedding into efferent blood of mamaria adenocarcinoma. Cancer Research. 1975;35(3):512-16.

9. Fidler IJ. Metastasis: quantitative analysis of distribution and fate of tumor emboli labelled with 125I-5-iodo-20-deoxyuridine. Journal Natl Cancer Inst. 1970;45(4):773-82.

10. Batson OV. The function of the vertebral veins and their role in the spread of metastasis. Ann Surg. 1940;112:138-49.

11. Franks LM. The spread of prostatic carcinoma to the bones. J Pathol Bacteriol. 1953;66(1):91-3.

12. Willis RA. The spread of tumors in the human body. 2a. ed. London: Butterworth Co.; 1973. p. 447.

13. Clohisy DR. Ramnaraine ML. Osteoclasts are required for bone tumors to grow and destroy bone. J Orthop Res. 1998;16(6):660-6.

14. Hirbe AC, et al. The bisphospanate zoledronic acid decreases tumor growth in bone in mice with defective osteoclasts. Bone. 2009;44:908-16.

15. Ebert R, et al. Pulse treatment with zoledronic acid causes sustained commitment of bone marrow derived mesenchymal stem cells for osteogenic differentiation. Bone. 2009;44:858-64.

16. Paterson A. Management of cancer and bone: Trials and Tribulations. Bone. 2009;44:S51.

17. Freedman H, Pinho STR. Stability criteria for the cure state in a cancer model with radiation treatment. Nonlinear Analysis: Real World Applications. 2009;10(5):2709-15.

18. Zhou F, Cui S. Bifurcations for a multidimensional free boundary problem modeling the growth of tumor cord. Nonlinear Analysis: Real World Applications. 2009;10(5):2990-3001.

19. Salmon JM, Kilpatrick SE. Pathology of skeletal metastases. Orthop Clin North Am. 2000;31(4):537-44.

20. Clines GA, Guise TA. Molecular mechanisms and treatment of bone metastasis. Expert Rev Mol Med. 2008;10:e7.

21. Gupta GP, Massague J. Platelets and previous term metastasis next term revisited: a novel fatty link. J Clin Invest. 2004;114(12):1961-3.

22. Liotta LA, Kohn EC. The microenvironment of the tumour-host interface. Nature. 2001;411:375-9.

23. Garzón-Alvarado DA, Roa MA, Cortés CJ. Análisis por elementos finitos del proceso de regeneración ósea. Bogotá: Ed. Universidad Nacional de Colombia; 2004. p. 252.

24. Hadjidakis DJ. Androulakis II. Bone Remodeling. Annals New York Academy of Sciences. 2006;1092:385-96.

25. Ferrer-Cañabate J, Tovar I, Martínez P. Osteoprotegerina y Sistema RANKL/RANK: ¿el futuro del metabolismo óseo? An Med Intern. 2002;19(8):385-8.

26. Cowin SC. Bone Mechanics Handbook. 2a. ed. Florida: CRC Press; 2001. p. 980.

27. Eriksen EF, Axelrod DW, Melsen F. Bone histology and bone histomorphometry. Bone Histomorphometry. Nueva York: Raven Press, 1994:33-48.

28. Hofstetter W, Felix R, Cecchini MG. Colony-stimulating factors. En: Bilezikian JP, Raisz LG, Rodan GA, eds. Principles of Bone Biology. San Diego: Academic Press; 1996. p. 673-86.

29. Mundy GR. Metastasis to bone: causes, consequences and therapeutic opportunities. Nat Rev Cancer. 2002;2(8):584-93.

30. Tsukii K, Shima N, Mochizuki S, Yamaguchi K, Kinosaki M, Yano L, et al. Osteoclast differentiation factor mediates an essential signal for bone resorption induced by 1 alpha, 25-dihydroxyvitamin D3, prostaglandin E2, or parathyroid hormone in the microenvironment of bone. Biochem Biophys Res Commun. 1998;256(2):337-41.

31. Bonewald LF, Dallas SL. Role of active and latent transforming growth factor in bone formation. J Cell Biochem. 1994;55:350-7.

32. Raisz LG. Physiology and pathophysiology of bone remodeling. Clin Chem. 1999;45:1353-8.

33. Pratap J, Lian JB, Javed A, Barnes GL, Wijnen AJ. van, Stein JL, Stein GS. regulatory roles of Runx2 in metastatic tumor and cancer cell interactions with bone. Cancer Metastasis Rev. 2006;25(4):589-600.

34. Komarova SV, Robert JS, Dixon SJ, Sims SM, Wahl LM. Mathematical model predicts a critical role for osteoclast autocrine regulation in the control of bone remodeling. Bone. 2003;33(2):206-15.

35. Lemaire VL, Tobin FL, Greller LD, Cho CR, Suva Larry J. Modeling the interactions between osteoblast and osteoclast activities in bone remodeling. Journal of Theoretical Biology. 2004;229(3):293-309.

36. Moroz A, Crane MC, Smith G, Wimpenny DI. Phenomenological model of bone remodeling cycle containing osteocyte regulation loop. Biosystems. 2006;84(3):183-90.

37. Moroz A, Wimpenny DI. Allosteric control model of bone remodelling containing periodical modes. Biophysical Chemistry. 2007;127(3):194-212.

38. Wimpenny DI, Moroz A. On allosteric control model of bone turnover cycle containing osteocyte regulation loop. Biosystems. 2007;90(2):295-308.

39. Frost HM. Bone mass and the previous mechanostat. A proposal. Anat Rec. 1987;219:1-9.

40. Kroll MH. Parathyroid hormone temporal effects on bone formation and resorption. Bull Math Biol. 2000;62:163-88.

41. Garzón-Alvarado DA, García-Aznar JM, Doblaré M. Appearance and location of secondary ossification centers may be explained by a reaction-diffusion mechanism. Computers in Biology and Medicine. 2009;9(6):554-61.

42. Garzón-Alvarado DA, García-Aznar JM, Doblaré M. A reaction-diffusion model for long bones growth. Biomech Model Mechanobiol. 2009;8(5):381-95.

43. Brouwers JEM, Donkelaar CC van, Sengers BG, Huiskes R. Can the growth factors pthrp, ihh and vegf, together regulate the development of a long bone? Journal of Biomechanics. 2006;39(15):2774-82.

44. Piotrowska MJ, Angus SD. A quantitative cellular automaton model of in vitro multicellular spheroid tumour growth. Journal of Theoretical Biology. 2009;258(2):165-78.

45. Hoffman J. Numerical Methods for Engineers and Scientists. 2a. ed. New York: McGraw Hill; 2001. p. 823.

46. Hindie E, Zanotti-Fregonara P, Keller I, Duron F, Devaux JY, Calzada-Nocaudie D, et al. Bone metastases of differentiated thyroid cancer: impact of early 131I-based detection on outcome. Endocr Relat Cancer. 2007;14:799-807.

47. Garbayo AJ, Villafranca E, De Blas A, Tejero A, Eslava E, Manterola A, et al. Metastatic bone disease. Diagnosis and treatment. Anales del sistema sanitario de Navarra. 2004;27(3):137-54.

Recibido: 14 de noviembre de 2009.
Aprobado: 12 de diciembre de 2009.

Prof. Diego Alexander Garzón-Alvarado. Facultad Ingeniería. Universidad Nacional de Colombia, Bogotá. Email: [e-mail]