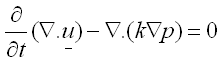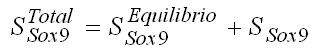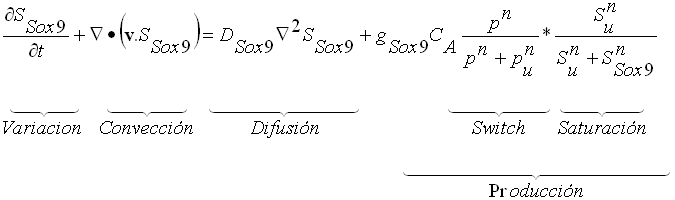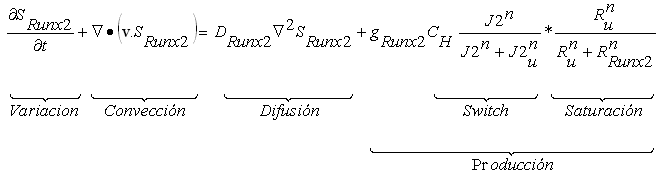ARTÍCULOS ORIGINALES

 

Acercamiento a la mecanobiología del cartílago articular a través de un modelo computacional

 

Approach to mechanobiology of articular cartilage through a computation model

Nancy Stella Landínez Parra^I; Diego Alexander Garzón Alvarado^II; Juan Carlos Vanegas Acosta^III

^IFisioterapeuta. Profesor Asistente. Facultad de Medicina. Universidad Nacional de Colombia, Bogotá.
^IIDoctor en Ciencias (PhD), Máster en Ciencias, Ingeniero Mecánico. Profesor Adjunto. Facultad de Ingeniería. Universidad Nacional de Colombia, Bogotá.

^IIIMáster en Ingeniería Biomédica. Grupo de Modelado y Métodos Numéricos en Ingeniería-GNUM. Universidad Nacional de Colombia, Bogotá.

 

 

---

RESUMEN

El cartílago articular es un complejo tejido biológico que recubre los extremos de las articulaciones diartrodiales y proporciona resistencia a la compresión y excelentes propiedades de fricción durante el movimiento articular. La presencia de cargas mecánicas influye en el comportamiento y condición fisiológica del cartílago. Es así como, mediante el mecanismo de mecanotrasducción, los condrocitos perciben la magnitud de la carga y a partir de éste estímulo mecánico expresan genes como el Sox9 o el Runx2, los cuales generan cambios bioquímicos en las células y por tanto en el cartílago mismo. Diferentes trabajos experimentales se reportan acerca del efecto de las cargas impuestas al cartílago relacionadas con la expresión morfogénica del condrocito, sin embargo, no se cuenta con un modelo matemático y/o computacional que pueda explicar el comportamiento antagónico del Sox9 y el Runx2. El objetivo de este trabajo es introducir un modelo matemático que permita predecir el comportamiento mecano-biológico del cartílago articular a partir de las cargas mecánicas cíclicas, la presión hidrostática y la expresión génica y/o de proteínas que facilitan el proceso de síntesis o destrucción del tejido. El modelo se implementó numéricamente con el uso del método de los elementos finitos y los resultados obtenidos permitieron predecir diversos comportamientos mecano-biológicos del cartílago articular.

Palabras clave: cartílago articular, condrocitos, modelado matemático, elementos finitos, mecanobiología, osteoartrosis, Sox9, Runx2.

---

ABSTRACT

Articular cartilage is a biological tissue complex coating the extremes of diarthric joints and provides resistance to compression and excellent friction properties during the articular movement. Presence of mechanical stress influenced on the behavior and physiologic condition of cartilage. That is how by means of the mechanotransduction, the chondrocytes may to perceive the stress magnitude and from this mechanical stimulus, they express gens like the Sox9 or the Runx2, which generate biochemical changes in cells and thus in the cartilage. Different experimental papers reporting on the effect of the stress imposed on the cartilage related to chondrocytes morphogenetic expression, however, there are not a mathematical model and/or computation to explain the antagonist behavior of Sox9 and the Runx2. The aim of present paper is to introduce a mathematical model allows predicting the mechano-biological behavior of articular cartilage from the cyclic mechanic stress, the hydrostatic pressure and the genic expression and or proteins providing the tissue synthesis or destruction. Model was numerically implemented using the finite elements method and the results obtained allowed to predict different mechano-biological behaviors of articular cartilage.

Key words: Articular cartilage, chondrocytes, mathematical modeling, finite elements, mechanobiology, osteoarthritis, Sox9, Runx2.

---

 

 

INTRODUCCIÓN

La osteoartritis (OA) es una causa común de dolor y discapacidad, especialmente en personas mayores. Se caracteriza por daño enzimático y mecánico de la matriz extracelular, que lleva a la degeneración del cartílago, exposición del hueso subcondral, formación de osteofitos marginales y a la inflamación de la membrana sinovial en la etapa clínica de la enfermedad.^1-3

El inicio y la progresión de la osteoartrosis están comúnmente afectados por factores mecánicos relacionados con la carga articular.⁴ La carga cíclica es el modo más común de carga en las articulaciones del miembro inferior del ser humano.⁵ Recientemente, existe gran interés por estudiar el efecto de las cargas dinámicas repetitivas sobre el cartílago articular, ya que la fuerza de contacto articular tiene un patrón cíclico durante las actividades diarias.^6-7 Algunos investigadores confirman que la fuerza mecánica que recibe una articulación puede regular las actividades metabólicas del cartílago articular en vivo.⁸

Los condrocitos secretan una matriz rica en colágeno tipo II y agrecanos y que expresan una característica genética programada por el SOX9 y otros homeogenes y factores de transcripción, que favorecen la formación y el mantenimiento de las proteínas propias del cartílago articular.⁹ Wong y colaboradores,¹⁰ plantearon que la expresión del Sox9 se regula por presión hidrostática, de igual forma, Smith y colaboradores¹¹ demostraron que niveles fisiológicos de presión hidrostática resultan en una regulación del colágeno tipo II y agrecanos, por lo que se considera un factor condrorregulador.

Por su parte, el homeogen Cbfa1/Runx2, es un importante regulador de la diferenciación de condrocitos. La sobreexpresión del Cbfa1/Runx2 en el cartílago de ratones transgénicos promovió la maduración de condrocitos hipertróficos y la osificación endocondral, mientras que la inhibición o la eliminación de la actividad del Cbfa1/Runx2, retardó o bloqueo la maduración de los condrocitos hipertróficos.^12-13

Los resultados a partir de los estudios de Inada y Cols.,¹⁴ muestran como el Cbfa1/Runx2 en ratones generó ausencia de expresión de la metaloproteinasa de la matriz MMP-13 y por lo tanto la inhibición de la degradación de la matriz del tejido; mientras que la sobreexpresión del Cbfa1/Runx2 aceleró la osificación endocondral por la maduración precoz de los condrocitos.¹² Como la actividad del Cbfa1/Runx2 es un factor determinante en la maduración de los condrocitos en la placa de crecimiento, puede ser un punto de referencia de la señalización anormal de los mecanismos que promuevan la iniciación y progresión de la OA.¹⁵

A pesar de contar con reportes de varias investigaciones que consideran el efecto de las cargas mecánicas sobre el tejido articular,^10,12,15-17 existe ausencia de modelos matemáticos o de simulación computacional, que permitan realizar comprender del comportamiento de los genes de expresión propios del cartílago. La mayoría de los estudios son experimentales, como el trabajo de Wang y Cols.,¹⁵ en el 2004, quienes detectaron por inmunohistoquímica, un mayor porcentaje de condrocitos con expresión Cbfa1/Runx2 en las articulaciones con OA en comparación con articulaciones de control (sin síntomas clínicos de OA) de edades similares. El relativo alto nivel de expresión del Cbfa1/Runx2 en relación con la OA avanzada, permite establecer una correlación entre la expresión génica observada en condrocitos articulares con OA respecto a la que normalmente se presenta en los condrocitos hipertróficos en las placas de crecimiento.¹⁵ Así, la sobre expresión de Cbfa1/Runx2 acelera la absorción de calcio y la actividad de fosfatasa alcalina,¹² lo cual puede asociarse con el inicio y la progresión de la OA dependientes de los cambios en la expresión génica de los condrocitos.¹⁵ Wong y Cols.,¹⁰ en el 2003 reportaron cómo la osificación endocondral se regula por varios factores, como los estímulos mecánicos, los cuales pueden suprimir o acelerar la maduración de los condrocitos.

Por lo tanto, en el presente trabajo se propone un modelo matemático que representa las principales características mecanobiológicas del cartílago articular. Se implementó un programa computacional para solucionar el modelo matemático propuesto. El objetivo del trabajo fue proporcionar una herramienta para la predicción de la expresión génica de moléculas en respuesta a las cargas mecánicas impuestas sobre el tejido, las cuales son percibidas por el condrocito mediante el mecanismo de mecanotrasducción, lo que condiciona de esta forma la expresión génica de las células. Se utilizó el método de los elementos finitos para realizar simulaciones que permitieron establecer la relación de dicha expresión génica con las cargas cortantes octaédricas y con la presión hisdrostática presentes en el cartílago como consecuencia de las cargas mecánicas. Esto permitió predecir la influencia de las cargas en la conservacion o degradación del cartílago articular y predecir el comportamiento de la expresión, así como el patrón de difusión de las moléculas que regulan el comportamiento del tejido.

Este trabajo inicia con una breve revisión acerca del mecanismo fisiológico de regulación de la matriz extracelular en el cartílago articular y contempla un acercamiento al modelado mecanobiológico, posteriormente se plantean los supuestos que metodológicamente soportan el modelo así como la forma de implementarlo. En la siguiente sección se realiza la discusión de los resultados obtenidos a partir de las simulaciones realizadas y se señalan nuevas líneas de investigación para el futuro.

Regulación de la matriz extracelular en el cartílago articular en función de las cargas

La topología histomorfológica del cartílago articular puede modificarse por la carga mecánica local que soportan los condrocitos en las distintas zonas del cartílago articular.¹⁸ De manera general, y bajo condiciones de equilibrio fisiológico, el cartílago articular adulto, está sujeto a un equilibrio entre los procesos anabólicos (síntesis de matriz extracelular) y catabólicos (degradación y pérdida de matriz), regulados, fundamentalmente por el condrocito. Esta respuesta se presenta por los factores en el microambiente, incluidas las fuerzas físicas o mecánicas, los factores de crecimiento, las citoquinas, el envejecimiento y la presencia de lesiones.^19-21 Se reporta que las cargas cíclicas son necesarias para el mantenimiento normal de la función del cartílago articular en las articulaciones diartrósicas.²²

De manera general, las propiedades mecánicas del cartílago articular (CA) se atribuyen a su estructura compleja y a la composición de su matriz extracelular (MEC) que comprende una fase de fluido (agua con iones disueltos), y una fase sólida (colágeno tipo II, agregados de proteoglicanos (PGs), proteínas, lípidos, y células).²³ Con la carga mecánica, el fluido intersticial se redistribuye a través de los poros de la matriz sólida permeable, con una conducta predominantemente poroelástica.²⁴

En vivo, las cargas de compresión articular pueden ser resistidas mediante tensiones en la fase sólida, y también por la generación de presión en la fase de fluido. La presurización de los fluidos en la superficie reduce la tensión impuesta a la matriz sólida y previene el excesivo desgaste y el daño del cartílago.¹⁸ Estas cargas inducen la deformación de la matriz del cartílago y causan alteración en la presión hidrostática, en la composición iónica y osmótica y en el fluido intersticial.²⁵ Como se mencionó anteriormente, algunos investigadores confirman que la fuerza mecánica sobre una articulación puede regular las actividades metabólicas del cartílago articular in vivo,⁸ entre ellas la diferenciación de los condrocitos.²⁶

Los cambios a partir de un estimulo mecánico impuesto al tejido, son percibidos por los condrocitos a través del mecanismo de mecanotrasducción.²⁷ La respuesta a éste estímulo coordina la expresión de genes, la síntesis de proteínas, la composición de la matriz y finalmente el desempeño biomecánico del tejido.²⁵ Por tanto, la mecánica puede controlar un proceso de regeneración o degradación de la matriz, de acuerdo a la magnitud y al tipo de carga que se imponga²⁷ (Fig. 1). En este sentido D'Lima y Cols.,²⁸ reportan que cargas por debajo de 7 Mpa no muestran muerte celular medible pero cargas por encima de 20 Mpa resultan en un extenso daño estructural del tejido.

Los condrocitos mantienen y remodelan la matriz del tejido cartilaginoso por un cuidadoso equilibrio de los procesos catabólicos y anabólicos que involucran la expresión de genes como el Sox9, el Cbfa1/Runx2 y su objetivo principal: las metaloproteinasas de la matriz (MMPs) y las metaloproteinasas inhibidoras de tejido (TIMPs). Durante la última década, dentro de los factores importantes en el control de crecimiento y desarrollo del cartílago se identificaron el Sox9 como un factor de transcripción que se expresa como condroprogenitor de los condrocitos diferenciados,³⁰ por su parte el Cbfa1/Runx2 acelera la osificación endocondral debido a maduración precoz de los condrocitos.¹² Los estudios de Ueta y Cols.,¹² también señalan que la activación de señalización Cbfa1/Runx2 en condrocitos inmaduros promueve la hipertrofia y la osificación endocondral precoz (Figs. 2 y 3).

En este contexto, algunos estudios demuestran que los niveles fisiológicos de presión hidrostática, resultan en una regulación del colágeno tipo II y agrecanos, los que constituyen una carga condroprotectiva.¹¹ Wong y Cols.¹⁸ describieron en el 2003 los valores normales de carga de los cartílagos articulares, que in vivo están expuestas a presiones de contacto entre 0 y 20 MPa, en frecuencias que van de 0,1 a 10 Hz. También reportan que los periodos de carga cíclica rara vez duran más de una hora y que éstos se intercalan con periodos de recuperación parcial y de plena recuperación total de al menos 16 horas por día.¹⁸

En este sentido Wong y Cols.,¹⁰ sugieren que la señalización Cbfa1/Runx2 puede proporcionar el vínculo molecular entre la carga mecánica y la maduración de condrocitos, en tanto que la presión hidrostática se traduce en una importante disminución de la expresión del MMP-13, lo que refuerza la hipótesis de que la presión hidrostática es condroprotectora. A su vez, los estudios de Wang y Cols.,¹⁵ en el 2004, detectaron por inmunohistoquímica, un mayor porcentaje de condrocitos con expresión Cbfa1/Runx2 en las articulaciones con OA en comparación con articulaciones de control de edad comparable.

La conservacion de la composición normal del cartílago requiere un nivel mínimo de carga y movimiento de la articulación. Sin embargo, una carga o movimientos repetidos de la articulación a un nivel mayor al considerado fisiológico, puede aumentar la actividad sintetizadora de los condrocitos.³¹ Un desequilibrio entre los procesos anabólicos y catabólicos puede llevar a la muerte celular y al deterioro funcional del tejido.¹⁹ El proceso degenerativo puede iniciarse con la pérdida de proteoglicanos de la MEC seguida de los trastornos de la red fibrilar de colágeno, lo cual es una de las características principales de la OA.

MÉTODOS

Las fuerzas mecánicas son importantes reguladores de la función primaria de los condrocitos y de la diferenciación de los progenitores. Numerosos estudios revelan los efectos de la compresión dinámica, la presión hidrostática, y las fuerzas cortantes sobre el metabolismo de los condrocitos articulares en explantes cultivados en gel. Las cargas mecánicas inducen deformación de la matriz del cartílago y causan alteración en la presión hidrostática, por lo tanto modifican la composición iónica y osmótica del fluido intersticial. Estos cambios son percibidos por los condrocitos, la respuesta a éste estímulo es diferencial según el tipo y la magnitud de la carga que el condrocito percibe y puede coordinarse para generar cambios en la expresión génica, en la síntesis de proteínas en la composición de la matriz y finalmente en el desempeño biomecánico del tejido.²⁵ Por tal razón éstas cargas determinan la conservación o no de la matriz del tejido mediante la activación de los morfogenes como el Sox9 y el Runx2.

Según lo planteado por Wong y Cols.¹⁰ y por Shieh y Cols.,²⁹ los condrocitos tienen la capacidad de detectar acciones mecánicas como la presión, la deformación y el flujo de fluido del tejido a través del mecanismo de mecanotransducción. Por tanto, los condrocitos pueden responder mediante la expresión de diferentes señales moleculares, tales como el Sox9 y el Runx2, y así controlan la histomorfologìa del cartílago articular. Este trabajo presenta un nuevo modelo mecanobiológico que permite cuantificar la expresión génica del Sox9 y del Runx2 y su correlación con los procesos de conservación o degradación de la matriz del tejido; se consideró el tejido como un material elástico, bajo cargas cíclicas, las cuales generan activación de los mRNA para el Sox9 y para el Runx2.

El modelo matemático

Las propiedades mecánicas del cartílago articular (CA) se atribuyen a su estructura compleja y a la composición de la MEC que comprende una fase de fluido (agua con iones disueltos), y una matriz solida (colágeno tipo II, agregados de PGs, proteínas, lípidos, y células).³² Con la carga mecánica, el fluido intersticial se redistribuye a través de los poros de la matriz sólida permeable, lo que da lugar a una conducta predominantemente poroelástica.

Varios autores^{23, 33-40} muestran el comportamiento bifásico que exhibe el cartílago. Esto permite modelar el material como un tejido poroelástico. La ecuaciones que rigen el comportamiento poroelástico dependen del desplazamiento u(t,x) del sólido (matriz) y la presión p(x) del fluido que es desplazado por la carga. Este modelo es descrito por las ecuaciones (1) y (2):⁴¹

(1)

(2)

donde:

es el esfuerzo sobre la matriz sólida y p es la presión del fluido. El término e (u) corresponde al tensor de deformación, m₅ y l₅ son las constantes elásticas de Lamé para el sólido, relacionadas con el módulo de Young y el coeficiente de Poisson (E, í); Ñ. u es la divergencia de los desplazamientos que representa la dilatación de la matriz, y k es la constante de permeabilidad del sólido ante el flujo del fluido intersticial.⁴²

Por tanto, la ecuación 1, de momentum, tiene en cuenta las cargas soportadas por el sólido y la presión sobre el fluido, a su vez la ecuación (2) representa la variación de la dilatación de la matriz sólida gracias a la distribución de presiones del fluido. En el caso del cartílago, al ejercer cargas sobre el tejido se produce exudación o imbibición del fluido, lo que altera, no solo el volumen de la articulación, sino además, el movimiento de diversos componentes que se transportan gracias al flujo.

Formulación para el Sox9

Uno de los factores más importantes para el control del crecimiento y desarrollo del cartílago, es el Sox9, éste se define como un factor de transcripción condroprogenitor que se expresa a nivel de los condrocitos diferenciados.³⁰ De manera general se puede decir que el Sox9, regula la expresión del colágeno tipo II, IX y XI, el agrecano, y el COMP en el desarrollo del cartílago,¹⁰ gracias al estímulo percibido por los condrocitos mediante la mecanotransducción.⁴¹

El Sox9 se identifica como un regulador del linaje de condrocitos. Es un factor de transcripción con una alta movilidad, del grupo (HMG), que se expresa en los condrocitos y otros tejidos.⁴² El Sox9 es un potenciador específico de los condrocitos que puede activar el potencial condrogénico aún en células no condrocíticas.⁴³ Como todos los factores de expresión génica el Sox9 se encuentra en el núcleo celular, y ante algunos estímulos, como la presión hidrostática, se activa para su posterior expresión en el citoplasma, mediante la acción del mRNA de Sox9.⁴⁴

En este trabajo se presupone que la expresión de Sox9 está dada por un valor de equilibrio que lleva a cabo el mantenimiento habitual del cartílago articular, además de la acción de las cargas mecánicas, en especial, la presión hidrostática, esto es:

(3)

donde, es la concentración total de Sox9 presente en cada punto del tejido y en cada instante, es el valor de la expresión normal de los condrocitos, en equilibrio y es la sobreexpresión de Sox9 debida a diferentes condiciones de carga y patologías del cartílago.

En este estudio, se presupone que la variación de la concentración de Sox9 depende de la presión hidrostática, por lo que:

(4)

en donde: v representa la velocidad del fluido debido a su condición poroelástica. D es el coeficiente de difusión del Sox9, g es el nivel de expresión de Sox9 por cada célula y C_A es la concentración celular de condrocitos metabólicamente activos. El término de producción del Sox9 se estableció en relación a la presión hidrostática (p) que percibe el condrocito, el umbral de activación debido a la carga mecánica (p_u) y el nivel umbral de concentración de moléculas de (S_sox9) presentes en el tejido.

De ésta forma, al nivel p_u de presión hidrostática (p) activa la expresión del Sox9. Además, el término de saturación determina a qué valor máximo S_u de Sox9 se satura la liberación molecular y se reduce su expresión.

En la figura 4 se muestran las funciones de liberación y saturación de Sox9 en función de la presión y la concentración molecular, respectivamente.

Formulación para el Runx2

La diferenciación de las células a lo largo del linaje osteoblástico se regula a nivel de la traducción del mRNA de Runx2. El Cbfa1/Runx2 es un factor de transcripción potenciador de la maduración de los condrocitos y de la diferenciación osteoblástica.⁴⁵ El Cbfa1/Runx2 es además un importante regulador de la diferenciación de condrocitos y se relaciona con la expresión de la MMP-13, la osteocalcina, y la fosfatasa alcalina en condrocitos hipertróficos así, como en osteoblastos. La sobreexpresión del Cbfa1/Runx2 acelera la osificación endocondral a través de la maduración precoz de los condrocitos.¹²

Wong y Cols.,¹⁰ reportaron que los esfuerzos de la matriz a partir de la carga cíclica mecánica que se aplicó a condrocitos primarios de bovinos por espacio de tres días, incrementó significativamente la expresión de Cbfa1/Runx2 (1,4 veces) y la MMP-13 (2,3 veces). Este nivel de carga, específicamente octaédrica llevó a la maduración temprana de los condrocitos, y los transformó en hipertróficos.

Bajo un enfoque similar al que se utiliza para el Sox9, en este trabajo se infiere que la expresión de Cbfa1/Runx2 está dada por un valor de equilibrio que lleva a cabo la degradación y recambio del cartílago, más un término que se modifica por las cargas mecánicas, en especial, los esfuerzos octaédricos, esto es:

(5)

donde, es la concentración total de Runx2 presente en cada punto del tejido y en cada instante, es el valor de la expresión normal de los condrocitos, en equilibrio, y, es la sobreexpresión de Runx2 secundaria a diferentes condiciones de carga y patologías del cartílago.

Para determinar la expresión del Runx2 (S_Runx2), que depende del nivel de esfuerzo octaédrico se supone la ecuación (6), dada por:

(6)

en donde v representa la velocidad del fluido, D es el coeficiente de difusión del Runx2, g es el nivel de expresión de Runx2 por cada condrocito que se encuentra en la región pre-hipertrófica. El término de producción del Runx2 se establece sobre el criterio del esfuerzo cortante octaédrico, específicamente de la variante (J2) de la matriz de esfuerzo, que percibe el condrocito.

Por su parte, el término que representa el switch, activa la expresión del Runx2 a ciertos niveles de presión octaédrica (Ju). La demarcación de saturación, determina a qué valor de Runx2 se disminuyó la liberación del mismo. La forma de las gráficas de activación y saturación son iguales a las supuestas para el Sox9.

Determinación de los parámetros del modelo para el Sox9 y para el Runx2

El conjunto de ecuaciones que se presentaron anteriormente, corresponde a un sistema integral. Las variables a resolver en este modelo incluyeron parámetros de reacción-difusión que describen las interacciones químicas que generan patrones en el espacio y/o el tiempo, secundarios a la presencia de términos de transporte, síntesis y degradación.

Las variables objeto de análisis constituyeron factores moleculares, como la expresión del Sox9 y del Runx2, que se asociaron a procesos difusivos, como consecuencia de la modificación de presiones o deformaciones. Los datos de referencia tales como la concentración celular de condrocitos activos e hipertróficos y las concentraciones de Sox9 y de Runx2 proveyeron valores cercanos a la magnitud real, que pueden presentarse en un experimento sobre expresión génica, en presencia de soporte de cargas octaédricas o de presiones hidrostáticas.

A continuación se muestran los parámetros para el diseño del modelo, para el cálculo de la expresión del Sox9 y del Runx2; estos se calculan a partir de datos de experimentación numérica y biológica de modelos semejantes al que se plantea en este trabajo (ver tabla).

Implementación

Este modelo fue resuelto numéricamente con base en el método de los elementos finitos.⁵³ La solución a este problema se implementó con el uso de una rutina de usuario que se programó en FORTRAN y se solucionó con la ayuda de ABAQUS 6.5.1 por medio de una sub-rutina UEL⁵³ en un PC con procesador AMD de 2.4 GHz y 1.0 GB de memoria RAM.

Se modeló un segmento de la articulación de rodilla (20 mm), con y sin menisco. En ambos casos se representaron: una porción de cóndilo femoral, el hueso esponjoso, el hueso subcondral y el cartílago articular que soporta las cargas. Para el caso del modelo con menisco se consideró además del menisco, una delgada membrana flexible, pues se conoce que el contacto entre 2 o más cuerpos deformables pueden provocar graves dificultades en los cálculos con el método de los elementos finitos. Esta membrana se diseñó con baja rigidez para ubicarse entre el cartílago y el menisco y supuso una interfase entre los dos tejidos (Fig. 4.3b), de manera análoga al trabajo de Wilson y colaboradores.⁵⁴

El cartílago se consideró con una profundidad de 4 mm, para lo cual se realizó una malla de 5 100 elementos y 5 253 nodos correspondiendo 4 nodos para cada elemento en el caso del modelo sin menisco (en la Fig. 5 ver 5.3a) y de 3 592 nodos y 3 443 elementos para el modelo con menisco (5.3b).

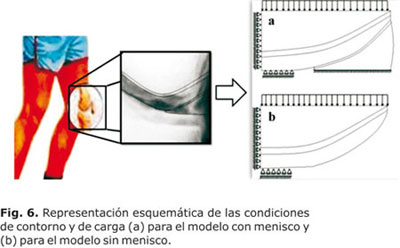
Se simuló una condición de confinamiento del tejido en la forma que indica la figura 6. Se aplicó una carga en el borde superior de 0,63662 por cada elemento en el caso de la carga normal (80 kg de peso corporal) y de 1,27324 para cada elemento cuando se realizaron simulaciones con sobrecarga (160 kg de peso corporal).

RESULTADOS

Las respuestas del modelo propuesto con integridad del menisco pueden observarse en las figuras de la 6 a la 9, mientras que los resultados del modelo sin menisco pueden observarse en las figuras de la 10 a la 13.

Modelo con menisco

El modelo de la simulación representa la mitad de un cóndilo femoral con soporte de menisco. La figura 7 representa la expresión del Sox9 en respuesta las presiones hidrostáticas percibidas a partir de las cargas impuestas al tejido. Se muestra la presión hidrostática soportada por el cartílago, ésta es mayor en la región central del cartílago, lugar en donde el tejido percibe mayores esfuerzos. De igual forma se puede evidenciar el incremento en la expresión del Sox9 con respecto al tiempo, la cual se inicia en el sitio de mayor presión hidrostática que posteriormente se propaga a lo largo de todo el cartílago.

La figura 8 representa la expresión del Sox9 en respuesta a las presiones hidrostáticas resultantes de la sobrecarga impuesta al cartílago. Al duplicar la carga, se consigue una duplicación de la presión hidrostática lo que determina, así mismo, un incremento en la expresión del Sox9, en respuesta a la presión (efecto condroprotector).

Por su parte, la expresión del Runx2 en relación con la presión octaédrica, se aprecia en la figura 9, en donde se evidencia cómo en condiciones de carga normal la presión octaédrica se incrementó a través del tiempo y llegó a valores de 1,4 MPa. Este incremento generó una activación en la expresión del Runx2, la cual se inició en el sitio de mayor concentración de esfuerzos de la capa profunda del cartílago, cerca de la unión con el hueso subcondral el cual se propagó a lo largo de todo el tejido con el paso del tiempo.

Al incrementar la carga (sobrecarga), se apreció que la presión octaédrica se duplicó y se incrementó la expresión del Runx2 (Fig. 9). En ambos casos (con carga dentro de rangos normales y en sobrecarga) se apreció un desequilibrio entre la expresión del Sox9 y del Runx2, lo que favoreció la degradación de la matriz (Fig. 10).

Modelo sin menisco

Al igual que en el modelo con menisco, en la simulación se utilizó un modelo que representó la mitad de un cóndilo femoral pero en este caso sin el soporte del menisco (meniscectomía). Los resultados se pueden apreciar en las figuras 11 a 14.

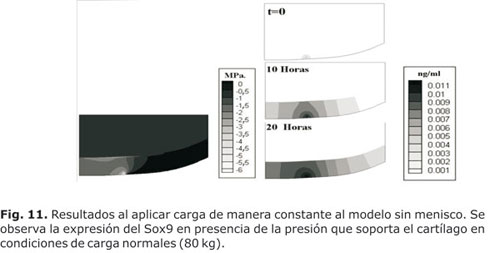
En la figura 11 se observa como la presión hidrostática (PresH) que soportó el cartílago presentó una mayor variación ante la aplicación de las cargas en el tiempo, en comparación con el modelo con menisco, el cual permitió variaciones en rangos muy pequeños. Esto hizo que la expresión del Sox9 fuera mayor que la exhibida en el modelo con menisco.

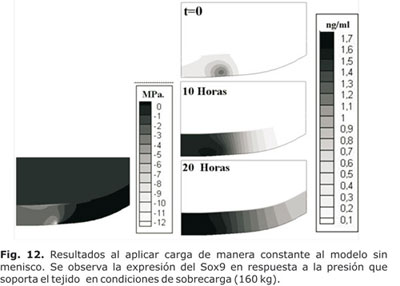
A su vez, la figura 12 representa el mismo modelo pero en una simulación con sobre carga (160 kg de peso corporal). Es fácil apreciar como la presión hidrostática se duplicó pero el crecimiento en la expresión del Sox9 se incrementó mucho más que el doble, lo que refuerza la teoría que una presión hidrostática fisiológica (10 a 20 MPa) multiplica la expresión del Sox9, que se convierte en un estímulo condroprotector.

La expresión de Sox9 se presentó en la zona media del cartílago, que correspondió a la región en donde se encuentraron los condrocitos metabólicamente activos, de igual forma se apreció que ésta expresión se inició desde el lugar de mayor deformación por presión (lo cual puede significar un inicio de daño) y se propagó a lo largo de todo el cartílago.

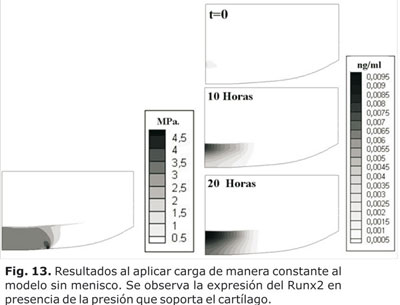
La expresión del Runx2 para el modelo sin menisco, como consecuencia de la presión octaédrica que soportó el tejido ante la carga, se representó en la figura 13. En una condición de carga habitual (80 kg de peso corporal), se evidenció que la expresión del Runx2, fue menor que la expresión del Sox9para este mismo modelo (Fig. 11). Esto puede interpretarse como un proceso natural de mantenimiento de la MEC.

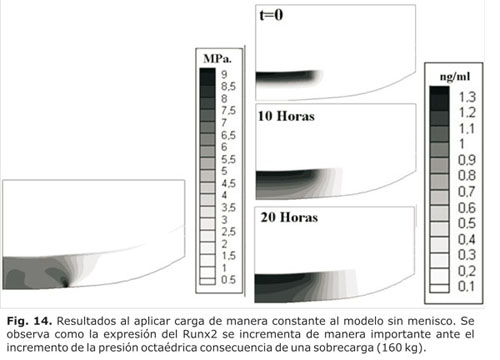
Sin embargo, la figura 14 evidencia que al duplicar la presión octaédrica cuando se simuló una condición de sobrecarga (160 kg de peso corporal), se incrementó de manera muy importante la expresión de Runx2, lo cual favoreció la degradación de la matriz extracelular (dado que el Runx2 facilita la expresión de las MMPs que son proteínas que degradan la MEC), en comparación con la respuesta obtenida al aplicar una carga normal de peso, en donde la expresión del Runx2 fue menor.

En la figura 14 puede notarse como la expresión de Runx2 se originó a partir de la zona más profunda del cartílago que se encontró en contacto con el hueso subcondral y poseyó condrocitos pre-hipertróficos, lo cual se correlacionó con el hecho que el Cbfa1/Runx2 fue un importante regulador de la diferenciación de condrocitos.^12-13 Aunque la expresión del Runx2 se inició en la unión del cartílago con el hueso sub-condral, ésta se propagó a lo largo de toda la zona del tejido e inició así un proceso osteoartrósico. Esto explica el adelgazamiento del cartílago y el incremento en la región del hueso sub-condral en los procesos osteoartrósicos, descritos por varios autores entre ellos Fukuda y Cols.⁵⁵

DISCUSIÓN

En un esfuerzo por comprender la mecanobiología del cartílago, múltiples investigaciones se desarrollaron en los últimos años con una variedad de protocolos experimentales in vitro e in vivo que permiten entender y confirmar el comportamiento del cartílago articular ante la imposición de cargas mecánicas.^56-59

Los resultados a partir de la simulación con los modelos de trabajo, permiten evidenciar que el cartílago sometido a cargas continuas en el tiempo, puede desencadenar la activación de moléculas como el Sox9 o el Runx2. Sin embargo, se evidenció que la presencia de los meniscos constituyó un factor determinante de protección, en la respuesta del cartílago articular, ante las cargas mecánicas. Esto condicionó mejor distribución de las cargas en una región más extensa del mismo, hizo posible que el soporte de presión octaédrica por parte de la matriz y el incremento de la presión hidrostática en su interior fueran menores.

Lo anterior se correlaciona con lo reportado por otros autores,^60-62 quienes plantearon que el normal desarrollo, crecimiento y mantenimiento del tejido cartilaginoso depende de factores mecánicos de carga y bioquímicos, como la expresión osteoblástica o condroblástica. Diversos estudios reportan cómo, la deformación secundaria a las cargas mecánicas impuestas, facilita la degradación de la matriz del cartílago, mientras que las presiones hidrostáticas son condroprotectoras. De igual forma, algunos autores también reportan cómo el flujo de diversas sustancias modula la actividad de biosíntesis de los condrocitos.^60-62

Las simulaciones permitieron evidenciar cómo en el modelo con menisco, la expresión de Runx2 fue menor en comparación con el modelo sin menisco. De manera análoga la mejor distribución de las carga a lo largo del tejido en el modelo con menisco hizo que la presión hidrostática no presentara grandes transformaciones como sí lo ocurrió en el modelo sin menisco, lo que obligó al condrocito a emitir una mayor respuesta de protección en la regulación de la matriz extracelular del mismo.

En éste sentido, fue importante plantear como el correcto balance entre los factores catabólicos y anabólicos permitió mantener una adecuada expresión del cartílago articular en condiciones de presión hidrostática fisiológica. Sin embargo, un incremento de la carga cíclica o de la presión hidrostática más allá de las cargas consideradas como fisiológicas a nivel articular^28,63 desencadenó un daño a nivel de la matriz con la consiguiente alteración del tejido. Esto se ilustra en la figura 15.

Los resultados de este trabajo igualmente se correlacionan con los hallazgos de Wong y Cols.,¹⁰ quienes plantearon la hipótesis de que los genes que se vinculan a la hipertrofia y a la osificación pueden ser regulados por la tensión cíclica y que los genes que se asocian con la condrogénesis reciben la acción reguladora de la presión hidrostática.¹⁰

A pesar de que los resultados se correlacionan con otros estudios experimentales, se hace necesario continuar con los estudios que permitan verificar las condiciones fisiológicas, tanto para carga cíclica como para presión hidrostática en el cartílago, y se debe considerar no solamente la magnitud, sino el tiempo de aplicación de la misma. Esto permitirá entender los mecanismos del daño articular en función de las cargas mecánicas y de la expresión de factores génicos que se generan a partir de ellas.

REFERENCIAS BIBLIOGRÁFICAS

1. Silver FH, Bradica G, Tria A. Relationship among biomechanical, biochemical, and cellular changes associated with osteoarthritis. Biomedical Engineering. 2001;29(4):373-91.

2. Silver FH, Bradica G, Tria A. Do changes in the mechanical properties of articular cartilage promote catabolic destruction of cartilage and osteoarthritis?. Matrix Biology. 2004;23:467-76.

3. Sniekers YH, Weinans H, Bierma-Zeinstra SM, van Leeuwen JPTM, van Osch GJVM. Animal models for osteoarthritis: the effect of ovariectomy and estrogen treatment a systematic approach. Osteoarthritis and Cartilage. 2008;16,533-41.

4. Andriacchi TP, Mündermann A, Smith RL, Alexander EJ, Dyrby CO, Koo SA. A framework for the in vivo pathomechanics of osteoarthritis at the knee. Annals of Biomedical Engineering. 2004;32:447-57.

5. Seedhom BB, Wallbridae NC. Walking activities and wear of prostheses. Annals of the Rheumatic Diseases. 1985;44:838-43.

6. Afoke NYP, Byers PD, Hutton WC. Contact pressures in the human hip joints. Journal of Bone Surgery. 1987;69:536-41.

7. Krishnan R, Mariner EN, Ateshian GA. Effect of dynamic loading on the frictional response of bovine articular cartilage. Journal of Biomechanics. 2005;38:1665-73.

8. Kiviranta I, Tammi M, Jurvelin J, Saamanen AM, Helminen H. Moderate running exercise augments glycosaminnglycans and thickness of articular cartilage in the knee joint of young beagle dogs. Journal of Orthopaedics Research. 1988;6:188-95.

9. Kronenberg HM. Developmental regulation of the growth plate. Nature. 2003;3:423.

10. Wong M, Siegrist M, Cao X. Cyclic compression of articular cartilage explants is associated with progressive consolidation and altered expression pattern of extracellular matrix proteins. Matrix Biology. 199;18:391-99.

11. Smith RL, Carter DR, Schurman DJ. Pressure and Shear Differentially Alter Human Articular Chondrocyte Metabolism. Clinical Orthopaedics and Related Research. 2004;427S:S89-S95.

12. Ueta C, Iwamoto M, Kanatani N, Yoshida C, Liu Y, Enomoto-Iwamoto M, et al. Skeletal Malformations Caused by Overexpression of Cbfa1 or its Dominant negative form in chondrocytes. The Journal of Cell Biology. 2001;153:87-99.

13. Stricker S, Fundele R, Vortkamp A, Mundlos S. Role of Runx Genes in Chondrocyte Differentiation. Developmental Biology. 2002;245:95-108.

14. Inada M , Yasui T, Nomura S, Miyake S, Deguchi K, Himeno M, et al. Maturational disturbance of chondrocytes in Cbfa1-deficient mice. Developmental Dynamics. 1999;214:279-90.

15. Wang X, Manner PA, Horner A, Shum L, Tuan RS, Nuckolls GH. Regulation of MMP-13 expression by RUNX2 and FGF2. Osteoarthritic cartilage. Osteoarthritis and Cartilage. 2004;12:963-73.

16. Vanderploeg EJ. Mechanotransduction in engineered cartilaginous tissues: in vitro oscillatory tensile loading. (Tesis Doctoral). Georgia Institute of Technology. 2006.

17. Connelly JT. Regulatory mechanisms in the chondrogenesis of Mesenchymal progenitors: the roles of cyclic Tensile loading and cell-matrix interactions. (Tesis Doctoral). Georgia Institute of Technology. August 2007.

18. Wong M, Carter D. Articular cartilage functional histomorphology and mechanobiology: a research perspective. Bone. 2003;33:1-13.

19. Nesic D, Whiteside R, Brittberg M, Wendt D, Martin I, Mainil-Varlet P. Cartilage tissue engineering for degenerative joint disease. Advanced Drug Delivery Reviews. 2006;58:300-22.

20. Bay-Jensen AC, Andersen TL, Charni-Ben Tabassi N, Kristensen PW, Kjaersgaard-Andersen P, Sandell L, et al. Biochemical markers of type II collagen breakdown and synthesis are positioned at specific sites in human osteoarthritic knee cartilage. Osteoarthritis and Cartilage. 2007;15:456-62.

21. Lotz M, Blanco FJ, Von Kempis J, Uler J, Maier R, Villiger PM, et al. Cytokine regulation of chondrocyte function. Journal of Rheumatology. 1995;43:104-8.

22. Chahine NO, Ateshian GA, Hung CT. The effect of finite compressive strain on chondrocyte viability in statically loaded bovine articular cartilage. Biomechanics Model Mechanobiology. 2007;6:103-11.

23. Haider MA, Guilak F. Application of a three-dimensional poroelastic BEM to modelling the biphasic mechanics of cell_matrix interactions in articular cartilage. Computer methods in applied mechanics and engineering. 2007;196:2999-3010.

24. Wilson W. An explanation for the onset of mechanically induced cartilage damage. (Tesis Doctoral). Technische Universiteit Eindhoven. Eindhoven, 2005.

25. Garima S, Saxenaa RK, Mishra P. Differential effects of cyclic and static pressure on biochemical and morphological properties of chondrocytes from articular cartilage. Clinical Biomechanics. 2007;22:248-55.

26. Smith RL, Carter DR, Schurman DJ. Pressure and shear differentially alter human articular chondrocyte metabolism. Clinical Orthopaedics and Related Research. 2004;427S:S89-S95.

27. de Crombrugghe B, Lefebvre V, Nakashima K. Regulatory mechanisms in the pathways of cartilage and bone formation. Current Opinion in Cell Biology. 2001;13:721-7.

28. D'Lima DD, Hashimoto S, Chen PC, Colwell CW, Lotz MK. Human chondrocyte apoptosis in response to mechanical injury. Osteoarthritis and Cartilage. 2001;9:712-19.

29. Shieh AC, Athanasiou AK. Principles of Cell Mechanics for Cartilage Tissue Engineering. Annals of Biomedical Engineering. 2003;31:1-11.

30. Papadopoulou AK, Papachristou DJ, Chatzopoulos SA, Pirttiniemi P, Papavassiliou AG, Basdra EK. Load application induces changes in the expression levels of Sox-9, FGFR-3 and VEGF in condylar chondrocytes. Federation of European Biochemical Societies-FEBS Letters. 2007;581:2041-6.

31. Buckwalter JA, Mankin MD. Articular cartilage, part I: Tissue design and chondrocyte matrix interactions. Journal of Bone and Joint Surgery. 1997;79:600-11.

32. Haider MA, Guilak F. Application of a three-dimensional poroelastic BEM to modelling the biphasic mechanics of cell-matrix interactions in articular cartilage. Computer methods in applied mechanics and engineering. 2007;196:2999-3010.

33. Mow VC, Kuei SC, Lai WM, Armstrong CG. Biphasic creep and stress relaxation of articular cartilage in compression: theory and experiments. Journal of Biomechanical Engineering. 1980;102:73-84.

34. Haider MA, Schugart RC. A numerical method for the continuous spectrum biphasic poroviscoelastic model of articular cartilage. Journal of Biomechanics. 2006;39:177-83.

35. Wilson W, Van-Donkelaar CC, Van-Rietbergen B, Huiskes R. A fibril-reinforced poroviscoelastic swelling model for articular cartilage. Journal of Biomechanics. 2005;38:1195-204.

36. Meng XN, Leroux MA, Laursen TA, Setton LA. A nonlinear finite element formulation for axisymmetric torsion of biphasic materials. International Journal of Solids and Structures. 2002;39:879-95.

37. Wu JZ, Herzog W, Epstein M. An improved solution for the contact of two biphasic cartilage layers. J Biomechanics. 1997;30,4:371-5.

38. Terada K, Ito T, Kikuchi N. Characterization of the mechanical behaviors of solid-fluid mixture by the homogenization method. Computer methods in applied mechanics and engineering. 1998;153:223-257.

39. Donzelli PS, Spilker RL, Ateshian GA, Mow VC. Contact analysis of biphasic transversely isotropic cartilage layers and correlations with tissue failure. Journal of Biomechanics. 1998;32:1037-47.

40. Donzelli PS, Spilker RL. A contact finite element formulation for biological soft hydrated tissues. Computer methods in applied mechanics and engineering. 1998;153:63-79.

41. Frijns AJH. A Four-Component Mixture Theory Applied to Cartilaginous Tissues. (Tesis Doctoral). Eindhoven University of Technology. 2000.

42. Zhao Q, Eberspaecher H, Lefebvre V, de Crombrugghe B. Parallel expression of Sox9 and Col2a1 in cells undergoing chondrogenesis. Developmental Dynamics. 1997;209:377-386.

43. Bridgewater LC, Lefebvre V, de Crombrugghe B. Chondrocyte-specific enhancer elements in the Col11a2 gene resemble the Col2a1 tissue-specific enhancer. Journal of Biology Chemycal. 1998;273:14998-15006.

44. Gilbert SF. Biología del Desarrollo. Madrid: Ed. Médica Panamericana. 2003.

45. Ueta C, Iwamoto M, Kanatani N, Yoshida C, Yang L, et al. Skeletal malformations caused by overexpression of Cbfa1 or Its dominant negative form in chondrocytes. The Journal of Cell Biology. 2001;153:88-99.

46. Kelly DJ, Prendergast PJ. Mechano-regulation of stem cell differentiation and tissue regeneration in osteochondral defects. Journal of Biomechanics. 2005;38:1413-22.

47. Garzón GA. Simulación de procesos de reacción-difusión: aplicación a la morfogénesis del tejido óseo. (Tesis Doctoral), Centro Politécnico Superior de la Universidad de Zaragoza. 2007.

48. Garzón-Alvarado DA, García-Aznara JM, Doblaré M. Appearance and location of secondary ossification centres may be explained by a reaction-diffusion mechanism. Computers in Biology and Medicine. 2009;39:554-61.

49. Garzón-Alvarado DA, García-Aznara JM, Doblaré M. A reaction-diffusion model for long bones growth. Biomechanics Models of Mechanobiology. 2009;8:381-95.

50. García-Aznar JM, Kuiper JH, Gómez-Benito MJ, Doblaré M, Richardson JB. Computational simulation of fracture healing: influence of inter fragmentary movement on the callus growth. Journal of Biomechanics. 2007;40(7):1467-76.

51. Geborek P, Forslind K, Wollheim FA. Direct assessment of synovial blood flow and its relation to induced hydrostatic pressure changes. Annals of the Rheumatic Diseases. 1989;48:281-6.

52. Hughes TJR. The finite element method. Linear static and dynamic finite element analysis. New York: Dover Publications, Inc. 2000.

53. Hibbit GH, Karlsson SE, Sorensen RT, Inc. Abaqus user's Manual, v. 6.5. HKS inc. Pawtucket, RI, USA, 2004.

54. Wilson W, Van Rietbergen B, Van Donkelaar CC, Huiskes R. Pathways of load-induced cartilage damage causing cartilage degeneration in the knee after meniscectomy. Journal of Biomechanics. 2003;36:845-51.

55. Fukuda Y, Takai S, Yoshino N, Murase K, et al. Impact load transmission of the knee joint-impudence of leg alignment and the role of meniscus and articular cartilage. Clinical Biomechanics. 2000;15:516-21.

56. Hong K, Na K. Effect of growth factors on chondrogenic differentiation of rabbit mesenchymal cells embedded in injectable hydrogels. Journal of Bioscience and Bioengineering. 2008;106,1:74-9.

57. Kurz B, Lemke AK, Fay J, Pufe T, Grodzinsky AJ, M. Schunke M. Pathomechanisms of cartilage destruction by mechanical injury. Annals of Anatomy. 2005;187:473-85.

58. Loening AM, James IE, Levenston ME, Badger AM, Frank EH, Kurz B, et al. Injurious mechanical compression of bovine articular cartilage induces chondrocyte apoptosis. Archives of Biochemistry and Biophysics. 2000;381,2:205-12.

59. Li Y, Tew SR, Russell AM, Gonzalez KR, Hardingham TE, Hawkins RE. Transduction of passaged human articular chondrocytes with adenoviral, retroviral, and lentiviral vectors and the effects of enhanced expression of SOX9. Tissue Engineering. 2004;10:575-84.

60. Mohtai M, Gupta MK, Donlon B, Ellison B, Cooke J, Gibbons G, et al. Expression of interleukin-6 in osteoarthritic chondrocytes and efects of flow-induced shear on this expression in normal human chondrocytes in vitro. Journal of Orthopaedic Research. 1996;14:67-73.

61. Das P, Schurman DJ, Smith RL. Nitric oxide and G proteins mediate the response of bovine articular chondrocytes to fluid induced shear. Journal of Orthopaedic Research. 1997;15:87-93.

62. Smith RL, Donlon BS, Gupta MK, Mohtai M, Das P, Carter DR, et al. Efects of fluid-induced shear on articular chondrocyte morphology and metabolism in vitro. Journal of Orthopaedic Research. 1996;13:824-31.

63. Bachrach NM, Mow VC, Guilak F. Incompressibility of the solid matrix of articular cartilage under high hydrostatic presures. Journal of Biomechanics. 1998;31:445-51.

Recibido: 22 de septiembre de 2009.
Aprobado: 8 de noviembre de 2009.

Nancy Stella Landínez Parra. Universidad Nacional de Colombia. Grupo de Modelado y Métodos Numéricos en Ingeniería. E mail: [e-mail]