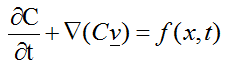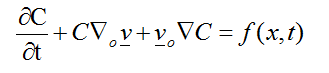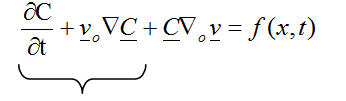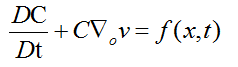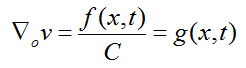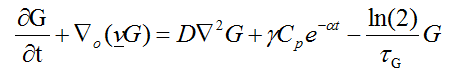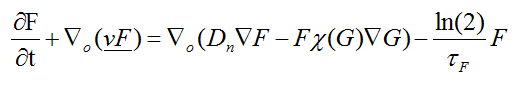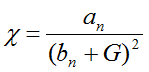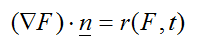ARTÍCULOS ORIGINALES

 

Modelo matemático del proceso de migración de fibroblastos en la lesión del ligamento

 

Mathematical model of fibroblast migration process in ligament lesion

 

 

Rosy Paola Cárdenas Sandoval^I; Diego Alexander Garzón Alvarado^II; Liliana Mabel Peinado Cortés^III

^IFisioterapeuta, Ingeniera de Sistemas. Facultad de Medicina. Universidad Nacional de Colombia.
^IIDoctor en Ciencias (PhD), Máster en Ciencias, Ingeniero Mecánico. Profesor Adjunto. Facultad de Ingeniería. Universidad Nacional de Colombia, Bogotá.
^IIIIngeniera Electrónica. Facultad de Medicina. Universidad Nacional de Colombia, Bogotá.

---

RESUMEN

La migración y proliferación de fibroblastos es una de las etapas más importantes en el proceso de reparación del ligamento tras sufrir ruptura parcial de sus fibras, esguince grado II. La evidencia experimental muestra que en esta etapa se produce la nueva matriz extracelular y en ella, los fibroblastos responden de manera favorable a los estímulos mecánicos e incrementan la síntesis de colágeno, elastina, proteoglicanos y factores de crecimiento, lo cual mejora las propiedades biológicas y mecánicas del tejido. El objetivo de este trabajo es proporcionar un modelo matemático con fundamento en las ecuaciones de reacción-difusión para describir el proceso de migración y proliferación de los fibroblastos. El modelo propuesto está resuelto mediante el método de elementos finitos. Los resultados obtenidos simulan la hemorragia, congestión y edema del tejido en el momento de sufrir la lesión, la liberación de factores de crecimiento, la migración y proliferación de los fibroblastos y la formación de las nuevas fibras de colágeno.

Palabras clave: ligamento, reparación, modelo matemático, ecuaciones de reacción-difusión, migración de fibroblastos, factores de crecimiento, esguince grado II.

---

ABSTRACT

Fibroblast migration and proliferation is one of the different and more important stages in ligament repair process after a partial rupture of its fibers, II degree sprain. Experimental evidence demonstrates that in this stage a new extracellular matrix is produced and there, the fibroblasts answer in a favorable way to mechanical stimuli and increase the collagen synthesis, elastin, proteoglycans and growth factors improving the tissue biological and mechanical properties. The aim of present paper is to provide a mathematical model based on reaction-diffusion equations to describe the fibroblasts migration and proliferation process. The model proposed is solved by means of the finite elements method. The results obtained simulate the hemorrhage, the congestion and tissue edema at moment of lesion, growth factor release, and fibroblast migration and proliferation as well as the formation of new collagen fibers.

Key words: Ligament, repair, mathematical model, reaction-diffusion equations, fibroblast migration, growth factors, II degree sprain.

---

 

 

INTRODUCCIÓN

La lesión del ligamento se conoce como esguince, se produce por una elongación máxima de las fibras causando ruptura parcial o total de las mismas.^1,2 En Estados Unidos se estima una prevalencia de 23 000 esguinces por día, en los Países Bajos asciende a 234 000 casos por año y el costo promedio anual de tratamiento se aproxima a los € 84, 240 000.³

De acuerdo al mecanismo de lesión puede clasificarse como esguince grado I, II y III,^4,5 en el grado I, si bien no existe ruptura de las fibras, la carga mecánica ocasiona deformación lo que genera hiperlaxitud en el tejido. En el grado II, la carga excede el pico de fuerza tensil del ligamento y causa por lo general, ruptura parcial de las fibras, de no ser así produce fallas microscópicas y deja al tejido susceptible de ruptura. En el grado III, la carga excede el pico de fuerza tensil hasta alcanzar su rompimiento total.^6,7

Numerosos estudios se dedican a describir la recuperación del ligamento tras la ruptura completa de sus fibras con el fin de evaluar la mejor técnica quirúrgica de reconstrucción, sin embargo, muy poco se sabe acerca del proceso de reparación del tejido tras sufrir un esguince grado II⁸ el cual puede curarse espontáneamente con tratamiento conservador⁹ y es de gran importancia para los fisioterapeutas y kinesiólogos.

Algunos acercamientos a esta lesión realizaron Provenzano y Cols.,⁸ Woo y Cols.,¹⁰ y Frank y Cols.¹¹ Sus investigaciones permitieron identificar cuatro etapas de reparación tras la ruptura parcial de las fibras del ligamento: hemostasia, angiogénesis, proliferación y remodelación.

La fase de proliferación de fibroblastos es una de las más importantes en la reparación del tejido, no sólo porque allí se produce la síntesis de la nueva matriz extracelular¹² sino porque dicha etapa responde a los estímulos mecánicos aumentando la síntesis de matriz de extracelular: colágeno, elastina, proteoglicanos, citoquinas y factores de crecimiento,^6,13 lo cual mejora las propiedades mecánicas de las fibras.^14,15

En promedio, este proceso puede tardar 52 semanas sin llegar a alcanzar las propiedades biológicas y mecánicas del ligamento normal.¹⁰ Estas razones conducen a desarrollar modelos matemáticos que profundicen en los aspectos biológicos de dicho proceso y permitan realizar predicciones cuantificables de los factores que los afectan.

Como ejemplo de ello, es posible demostrar mediante la cuantificación de los esfuerzos que el ligamento lesionado bajo un tiempo determinado de reparación no alcanza las mismas propiedades mecánicas que el ligamento normal.¹⁷ Este trabajo desarrollado por Abramowitch y Cols., se logró con el empleo de la teoría quasi-lineal viscoelástica de Fung.

Otras aplicaciones desarrolladas en piel, reconocen los aspectos claves que deben tenerse en cuenta para favorecer la contracción de la herida, entre ellos la cinética de las células encargadas de realizar las fuerzas de tracción para generar la contracción de la herida, la cinética de degradación del colágeno y la producción de factores de crecimiento.^14,18 Trabajos cimentados en las ecuaciones de convección y las leyes constitutivas de viscoelasticidad ortotrópica.

Estas aplicaciones demuestran que el enfoque matemático puede complementar los hallazgos biológicos y experimentales del proceso de reparación, por ello, el objetivo de este trabajo es proponer un modelo matemático con fundamento en las ecuaciones de reacción-difusión para describir el proceso de migración y proliferación de los fibroblastos tras la ruptura parcial de las fibras del ligamento. Este trabajo es la base para continuar con próximas investigaciones que permitan describir los cambios biológicos ocurridos en el ligamento cuando está sometido a estímulos mecánicos con el fin de predecir las condiciones de la carga que puedan acelerar el tiempo de recuperación del tejido, hecho de gran interés para los deportistas de alto rendimiento.

En primera medida, se abordarán los aspectos biológicos implicados en la reparación del ligamento, bajo este marco de referencia se planteará el modelo matemático para describir el proceso de hemorragia, congestión y edema ocurridos en la primer fase; la liberación de los factores de crecmiento que activan la síntesis de fibroblastos, la migración y proliferación de dichas células y la formación de las nuevas fibras de colágeno. Se explicará la implementación numérica del modelo mediante el método de elementos finitos, los resultados obtenidos y se finalizará con la discusión.

MÉTODO

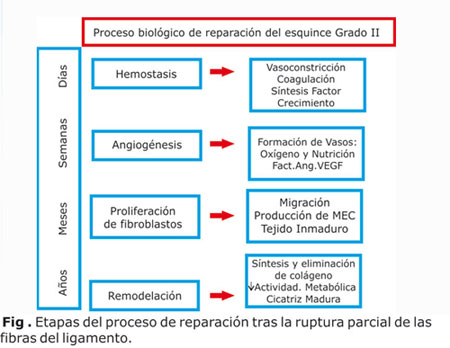
El proceso biológico de reparación en el esguince grado II, comprende cuatro fases hemostasia, angiogénesis, proliferación de fibroblastos y remodelación^11,19-21 (Fig. 1).

La primera etapa, hemostasia, ocurre durante las primeras 12 a 24 horas siguientes a la lesión.²² La ruptura de los vasos sanguíneos que irrigan el tejido produce hemorragia, congestión y edema en el área afectada, es decir aumento local del volumen de sangre, hinchazón sutil de las células y separación de los elementos de la matriz extracelular.^2,19

En aproximadamente ocho minutos, los vasos dañados sufren vasoconstricción para disminuir o parar la pérdida de sangre.²³ La colección de sangre en el sitio de la lesión hace que las plaquetas interactúen con la matriz extracelular lesionada para ejecutar dos procesos fundamentales: disparar la formación de coágulos a través de la inducción de trombina y de fibrina¹¹ y sintetizar el factor de crecimiento derivado de las plaquetas (PDGF), esencial para activar la migración y proliferación de los fibroblastos al sitio de la lesión.^20,23

De forma simultánea ocurre la etapa de angiogénesis o neo-vascularización. Simboliza la formación de nuevos vasos sanguíneos a partir de brotes o retoños producidos por vasos preformados con el objetivo de remover el dióxido de carbono y productos de desecho, proveer oxígeno y nutrientes al área lesionada.²³

Para llevar a cabo esta etapa, se requiere la interacción entre las células vasculares, la matriz extracelular y el factor de crecimiento endotelial vascular (VEGF), este último favorece la angiogénesis y aumenta la permeabilidad vascular, lo que da lugar al depósito de proteínas plasmáticas, fibrinógeno y fibronectina en la matriz extracelular, con el fin de proporcionar un estroma provisional para el ingreso de los fibroblastos.¹⁹

De dos a cuatro días después de la lesión se produce la etapa más importante del proceso de reparación del ligamento, la migración y proliferación de los fibroblastos.¹¹ Estas células viajan desde el epiligamento, capa superficial que rodea los haces de fibras, hasta la zona de lesión, activadas por los factores de crecimiento epidérmico (EGF) y derivado de las plaquetas (PDGF), los cuales son sido liberados previamente por el contacto producido entre las plaquetas y la matriz lesionada.^9,23

Los fibroblastos se deslizan a través de los filamentos de fibrina y las fibras de colágeno para llegar a la herida, una vez allí producen fibronectina, hialurón y más tarde, colágeno y proteoglicanos. Estas proteínas ayudan a construir la nueva matriz extracelular, abastecen de sustratos a las células de adhesión y regulan el movimiento y diferenciación de las células dentro de ésta misma.²⁰

Finalizando esta fase, desaparecen algunos capilares, hay menor densidad celular y existe una alta síntesis de colágeno tipo I aunque persiste la presencia de colágeno tipo III con enlaces orientados aleatoriamente.²⁴

Finalmente, se produce la etapa de remodelación, en esta media la matriz sintetizada y eliminada por meses y años.²⁵ El colágeno es degradado por metaloproteinasas específicas, reguladas por factores de crecimiento y producidas por fibroblastos, neutrófilos y macrófagos ubicados en el sitio de reparación. Como medida de balance, la remodelación de la matriz causa un detrimento en la actividad de las metaloproteinasas y un incremento en el tejido inhibitorio de las mismas, reducción en la densidad de macrófagos y fibroblastos, detención del crecimiento de capilares, reducción en el flujo sanguíneo y actividad metabólica.²⁰

Una vez que la cicatriz ha madurado, la fibronectina y el hialurón son eliminados y los haces de colágeno aumentan su diámetro, lo cual corresponde con el aumento de la fuerza tensil. Sin embargo, estas fibras de colágeno nunca lograrán la fuerza original del tejido normal.^10,11,20 En los experimentos realizados por Frank y Cols.,² se comprobó que el ligamento cicatrizado alcanzó tan solo el 30-40 % de las propiedades mecánicas del ligamento normal, las causas potenciales están relacionadas con la mala alineación de las fibras de colágeno.

Modelo matemático

La producción de hemorragia seguida por congestión y edema en la zona afectada, puede expresarse como:

(1)

El primer término de la ecuación, hace referencia al flujo de sangre en el área de lesión, la variable C, representa la concentración de sangre, congestión y edema, v simboliza el vector de velocidad y f (x,t) corresponde a la función de hinchazón. Al expandir la ecuación (1) se obtiene:

(2)

(3)

(4)

Dado que el volumen de sangre se mantiene constante durante la etapa de congestión, el primer término de la ecuación (4) también debe permanecer constante: , por tanto, el proceso de dilatación ocurre a expensas de:

(5)

Lo que equivale a:

(6)

Se sabe mediante la mecánica de medios continuos que la divergencia del vector de velocidad equivale a la traza de la velocidad de deformación:

(7)

De esta forma, la función g (x,t) es equivalente a la traza de la velocidad de deformación:

(8)

Por otro lado, la ecuación de contorno que dirige el flujo de sangre por la zona de lesión es:

(9)

Donde n corresponde al vector normal y la función f (t) simboliza la zona de plaquetas.

Una vez se produce el contacto entre las plaquetas y la matriz extracelular lesionada, las plaquetas liberan factores de crecimiento, los cuales viajan desde el sitio de lesión hasta el epiligamento con el objetivo de activar la migración y proliferación de los fibroblastos. La síntesis de los factores de crecimiento se representa como:

(10)

En la ecuación 10, G representa la concentración del factor de crecimiento derivado de las plaquetas (PDGF). El primer término, corresponde al flujo del factor de crecimiento en la zona de congestión y edema, el segundo término, hace referencia al componente convectivo y dilatacional, el tercer término pertenece al transporte de los factores en la congestión, donde D es el coeficiente de difusión del factor. El cuarto término, indica la producción espacial del factor causado por las plaquetas y el último término expresa la muerte del factor debido al tiempo medio de vida del mismo.

La ecuación de contorno que dirige el flujo de los factores de crecimiento, desde la zona de colágeno lesionada hasta la capa superior de epiligamento es:

(11)

La función h(t) simboliza la zona de colágeno lesionado.

Terminada la fase anterior, se produce la migración de los fibroblastos:

(12)

En la ecuación 12, F representa el componente celular, es decir los fibroblastos. El primer miembro de la ecuación expresa el flujo de las células hacia la zona de lesión y el segundo miembro, corresponde a la difusión de los fibroblastos dependiente de la cantidad de factor de crecimiento liberado y se expresa la relación de apoptosis o muerte celular programada de las células mediante el último término.

La variable X, se define como:

(13)

La ecuación de contorno que dirige el flujo de los fibroblastos desde la capa de epiligamento hacia la zona de lesión es:

(14)

A partir de la información disponible en la literatura^17,26,27 y mediante análisis numérico los parámetros utilizados en el modelo se resumen en la tabla 1.

Implementación numérica

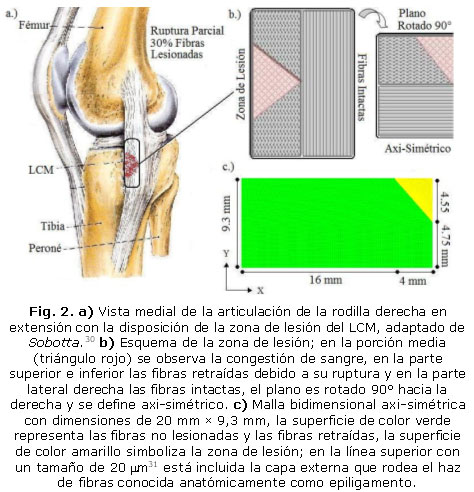
La implementación del modelo se realizó mediante el método de elementos finitos (Fig. 2) En primera medida se identificó la zona de lesión del ligamento colateral medial (LCM) (Fig. 2a), esta zona se aproximó al 30 % del total de fibras y se encontró ubicada en la porción media del tejido.^20,21 Se trazó la geometría preliminar de la zona de lesión (Fig. 2b), ésta fue rotada 90° y se eligió un plano axi-simétrico. Finalmente, el dominio se representó mediante una malla bidimensional de elementos lineales de cuatro nodos para cada elemento con dimensiones de 20 mm de longitud y 9,5 mm de ancho. Dicho dominio se dividió en dos superficies, la primera representa el área de fibras intactas y fibras retraídas (Fig. 2c) y la segunda (Fig. 2c) corresponde a la zona de lesión. La malla está formada en total por 20 371 nodos y 20 072 elementos.

En la ecuación de hemorragia, congestión y edema (1), se define la función f (t) (9) como condición para el contorno donde son depositadas las plaquetas por el flujo de sangre. La condición de flujo para el contorno de epiligamento equivale a la traza de la velocidad de deformación del tejido (7) y (8) para representar el edema del mismo.

Las condiciones iniciales para la ecuación de liberación del factor de crecimiento (10) corresponden a la función h (t) (11) para el contorno de colágeno, ubicado en la zona de matriz lesionada desde el cual se inicia la liberación del factor y valor 0, para el flujo en el contorno de epiligamento, sitio en el cual finaliza la liberación del factor.

En la ecuación de migración de los fibroblastos (12), se estableció la función r (s,t) (14), como condición para el contorno de epiligamento, desde el cual migran las células. La condición de flujo para el contorno correspondiente a la matriz lesionada se asumió igual a cero, sitio en el cual son confinados los fibroblastos.

El tiempo de la simulación correspondió con el tiempo aproximado de duración de la hemorragia, congestión, edema y liberación del factor de crecimiento, se aproximó a 3,33 horas. La implementación se desarrolló en un computador personal con procesador Core 2 Duo de 2,6 hz, memoria RAM de 2 GB y tardó 36 minutos en ejecutar la simulación.

RESULTADOS

El modelo presentado en este trabajo simboliza tres procesos fundamentales para la reparación del ligamento lesionado: congestión, liberación del factor de crecimiento y migración de los fibroblastos. El primero corresponde a la formación temporal de la congestión y el edema del tejido tras sufrir la ruptura parcial de sus fibras. Inmediatamente las plaquetas inmersas en este flujo se depositaron en la matriz lesionada para liberar el factor de crecimiento derivado de las plaquetas PDGF, segunda etapa, esencial para activar el componente celular de fibroblastos (Fig. 3). En la (Fig. 3a) se muestra el flujo inicial de sangre desde el contorno que representa la matriz lesionada, la concentración está dada en [ng/cc]. Pasados 27 minutos se evidenció un aumento en la concentración de sangre en la zona de lesión (Fig. 3b). Al cabo de 3,3 horas fue evidente la formación de congestión y edema (Fig. 3c).

Una vez los fibroblastos fueron activados por el factor de crecimiento derivado de las plaquetas PDGF, migraron desde la capa superficial de epiligamento hasta la zona de lesión (Fig. 4).

En la (Fig. 4a), se observa el momento inicial en el cual migran los fibroblastos desde la capa superficial de epiligamento hacia la matriz lesionada. La concentración estuvo dada en células/cc. Transcurridos dos días se evidenció difusión de los fibroblastos hacia la zona de la lesión (Fig. 4b). La difusión completa ocurrió cuatro días después de producida la lesión y puede durar semanas a meses.

DISCUSIÓN

En este trabajo se ha presentado un modelo matemático del proceso de migración de fibroblastos en el ligamento que ha sufrido ruptura parcial de sus fibras. Para ello, se han considerado tres sucesos: el primero, admite que tras la lesión debe producirse hemorragia para depositar las plaquetas en el sitio de la lesión,²³ como consecuencia se produce congestión y edema en la zona.¹⁹ En el momento en el que las plaquetas forman el coágulo inicial y se ha producido vasoconstricción para disminuir o parar la hemorragia, el volumen de sangre se mantiene constante y la hinchazón se produce a causa de la dilatación del tejido.

El segundo, asume que el contacto entre las plaquetas y la matriz lesionada produce la liberación de factores de crecimiento para activar la siguiente etapa de reparación,¹¹ se ha modelado el factor de crecimiento derivado de las plaquetas PDGF debido a que es el principal factor que activa la migración y proliferación de los fibroblastos.²⁷ Su desplazamiento inicia desde la matriz lesionada hacia la capa superficial de epiligamento.

El tercer suceso, comprende la migración de los fibroblastos desde la capa de epiligamento hacia la zona de lesión para dar inicio a la formación de la nueva matriz extracelular.^20,24 Este hecho depende de la cantidad del factor de crecimiento liberado.¹²

Bajo estas consideraciones el modelo predice la concentración de fibroblastos que migran al sitio de la lesión y el tiempo empleado para ello. Estos resultados permiten comparar situaciones en las que el tejido es altamente vascularizado como el ligamento colateral medial por su posición extra-articular y en condiciones de poca irrigación, como el ligamento cruzado anterior debido a su ubicación intra-articular.³²

No obstante, el modelo presenta varias limitaciones, entre ellas el valor de los parámetros del tiempo de vida promedio de los fibroblastos, velocidad y coeficiente de difusión. Para ello se recurrió a la literatura disponible para aproximar el modelo a la realidad del proceso de migración de los fibroblastos.

De otro lado, se asumió de manera general mediante la traza de la velocidad de deformación del tejido,⁷ el fenómeno de contracción de la zona de lesión, el cual depende de la nueva formación de los vasos sanguíneos, es decir, angiogénesis¹⁹ y de la fuerza de tracción realizada por las células para contraer el área de lesión.¹⁸

De igual manera, se espera desarrollar en futuras investigaciones la etapa de remodelación de las fibras de colágeno, la cual depende de los sucesos biológicos presentados en este trabajo. De acuerdo con la cantidad de fibroblastos depositados en la zona de lesión es posible predecir la cantidad de fibras de colágeno que serán producidas.²⁵ Además, será de gran interés para los fisioterapeutas y kinesiólogos mostrar el efecto que tiene la carga mecánica en la orientación de las fibras de tal forma sea posible optimizar las propiedades biológicas y mecánicas del tejido.¹⁵

AGRADECIMIENTOS

Este trabajo hace parte del proyecto "Modelo matemático del proceso mecanobiológico de reparación del ligamento" código DIB 202010013460, financiado por la Universidad Nacional de Colombia a través de la Convocatoria Apoyo a tesis de programas de Posgrado sede Bogotá - año 2009.

REFERENCIAS BIBLIOGRÁFICAS

1. Nobes L, Ryles R y Foreman K. A grade II medial collateral knee ligament sprain in a professional football player. Physical Therapy in Sport. 2000;1:42-53.

2. Frank CB, Hart DA, Shrive NG. Molecular biology and biomechanics of normal and healing. Osteoarthritis and Cartilage. 1999;7(1):130-40.

3. Hupperets DW, Verhagen EAM, Willem van M. Effect of unsupervised home based proprioceptive training on recurrences of ankle sprain: randomised controlled trial. BMJ. 2009;339:b2684.

4. De Vita R y Slaughter WS. A constitutive law for the failure behavior of medial collateral ligaments. Biomechan Model Mechanobiol. 2007;6:189-97.

5. Ivins D. Acute Ankle Sprain: An Update. American family Physician. 2006;74(10):1714-20.

6. Wang JH. Mechanobiology of tendon. Journal of Biomechanics. 2006;39:1563-82.

7. Subit D, et al. Microstructure of the ligament-to-bone attachment complex. Journal of the Mechanical Behavior of Biomedical Materials. 2008;360-7.

8. Provenzano PP, et al. Intrinsic fibroblast-mediated remodeling of damaged collagenous matrices in vivo. Matrix Biology. 2005;23(8):543-55.

9. Woo LY, et al. Engineering the healing of the rabbit medial collateral ligament. Medical & Biological Engineering & Computing. 1998;36:359-64.

10. Woo LY, et al. Biomechanics of knee ligaments: injury, healing, and repair. Journal of Biomechanics. 2006;39:1-20.

11. Frank CB, et al. Optimisation of the Biology of Soft Tissue Repair. Journal of Science and Medicine in Sport. 1999;2(3):190-210.

12. Hannafin JA, et al. Characterization of chemotactic migration and growth kinetics of canine knee ligament fibroblasts. J Orthop Res. 1999;17(3):398-404.

13. Denegar CR, Miller SJ. Can Chronic Ankle Instability Be Prevented? Rethinking Management of Lateral Ankle Sprains. Journal of Athletic Training. 2002;37(4):430-5.

14. Kjaer M, Magnusson SP. Mechanical Adaptation and Tissue Remodeling. En: Peter Fratzl. Collagen: Structure and Mechanics. s.l.: USA: Springer; 2008. p. 249-67.

15. Park SA, et al. Biological Responses of Ligament Fibroblasts and Gene Expression Profiling on Micropatterned Silicone Substrates Subjected to Mechanical Stimuli. Journal of Bioscience and Bioengineering. 2006;102(5):402-12.

16. Abramowitch SD, et al. An Evaluation of the Quasi-Linear Viscoelastic Properties of the Healing Medial Collateral Ligament in a Goat Model. Annals of Biomedical Engineering. 2004;32(3):329-35.

17. Javierre E, et al. Numerical modeling of a mechano-chemical theory for wound contraction analysis. International Journal of Solids and Structures. 2009;46:3597-606.

18. Flynn C, McCormack AO. A simplified model of scar contraction. Journal of Biomechanics. 2008;41:1582-9.

19. Cotran RS, Kumar V, Collins T. Robbins: Patología estructural y funcional. Madrid: Mc Graw Hill; 1999. p. 1475.

20. Enoch S, Leaper DJ. Basic science of wound healing. Surgery. 2007;26(2):31-7.

21. Provenzano PP, et al. Systemic administration of IGF-I enhances healing in collagenous extracellular matrices: evaluation of loaded and unloaded ligaments. BMC Physiology. 2007;7(2):1-17.

22. Márquez AJJ, Márquez WH. Lesiones del ligamento cruzado anterior de la rodilla. IATREIA. 2009;22(3):256-71.

23. Strecker-McGraw MK, Russel JT, Baer DG. Soft tissue wounds and principles of healing. Emerg Med Clin N Am. 2007;25:1-22.

24. Benani A, et al. How a daily and moderate exercise improves ligament healing. IRBM. 2008;29(4):267-71.

25. Cowin SC. Tissue growth and remodeling. Annu Rev Biomed Eng. 2004;6:77-107.

26. Brouwers JEM, et al. Can the growth factors PTHrP, Ihh and VEGF, together regulate the development of a long bone? Journal of Biomechanics. 2006;39:2774-82.

27. Creaney L, Hamilton B. Growth factor delivery methods in the management of sports injuries: the state of play. Br J Sports Med. 2008;42:314-20.

28. Doschak MR, Zernicke RF. Structure, function and adaptation of bone-tendon and bone-ligament complexes. J Musculoskelet Neuronal Interact. 2005;5(1):35-40.

29. Laws G, Walton M. Fibroblastic healing of grade II ligament injuries. The Journal of Bone and Joint Surgery. 1988;70-B:390-6.

30. Sobotta AM. Atlas de Anatomía Humana (T. II). 22 a. ed. Madrid: Panamericana; 2006, p. 1563-82.

31. Lo IKY, et al. The cellular networks of normal ovine medial collateral and anterior cruciate ligaments are not accuratelyrecapitulated in scar tissue. J Anat. 2002;200:283-96.

Recibido: 18 de septiembre de 2009.
Aprobado: 1ro. de diciembre de 2009.

Ing. Rosy Paola Cárdenas Sandoval. Facultad de Medicina. Universidad Nacional de Colombia. E mail: [e-mail]