TÉCNICAS

 

Modelo de remodelación ósea: un análisis computacional

Model of bone remodeling: a computed analysis

Henry Figueredo Losada^I; Vladimir González Fernández^II; Joan Batista Aguilar^III; Mikiya Muramatsu^IV; Angel Mario Felipe Garmendía^V

^IMSc. Ingeniero Mecánico. Asistente. Facultad de Mecánica, Grupo de Biomecánica, ISPJAE. La Habana, Cuba.
^IIDoctor en Ciencias Técnicas. Ing. Mecánico. Profesor Titular. Facultad de Mecánica, Grupo de Biomecánica, ISPJAE. La Habana, Cuba.
^IIIDr. en Ciencias Técnicas. Ing. Mecánico. Departamento de Mecánica, Universidad de Sao Paulo (USP), Brasil.
^IVDoctor en Ciencias Físicas. Departamento de Física General, Universidad de Sao Paulo (USP), Brasil.
^V Especialista de II Grado en Odontología. Asistente. Departamento de Cirugía Maxilofacial, Hospital Pediátrico "Juan Manuel Márquez", Cuba.

---

RESUMEN

En este trabajo se tomó el modelo de remodelación ósea propuesto por Jacob (1994) y se implementó en un programa de elementos finitos con el empleo de una subrutina de usuario (UMAT), este se aplicó a un modelo 2D de un hueso genérico con un sistema de cargas para comprobar los efectos de la remodelación y las variaciones de los valores de densidad. Como parte del trabajo fueron creados 2 programas para el procesamiento de los datos, para un análisis de resultados fuera del programa de elementos finitos; se logró una apreciación cualitativa y cuantitativa de los resultados obtenidos.

Palabras clave: Biomecánica, elementos finitos, remodelación ósea.

---

ABSTRACT

This paper takes the bone remodeling model proposed by Jacob (1994) and is implemented in a finite element program using a user subroutine (UMAT), and applied to a 2D model of a generic bone with a system of charges to test the effects of remodeling and changes in the density values. As part of this work were created two programs for processing data for analysis of results outside the finite element program, achieving a qualitative and quantitative assessment of the results.

Key words: Biomechanics, Finite element, Remodeling bone.

---

 

 

INTRODUCCIÓN

Dentro del gran abanico de aplicaciones que componen la Ingeniería Biomédica, se conoce como Biomecánica la disciplina que trata del análisis y predicción de la mecánica de los seres vivos y ayuda, por tanto, a entender el funcionamiento motor de los organismos, a caracterizar el comportamiento de tejidos y órganos vivos desde el punto de vista estructural y a predecir los cambios microestructurales que sufren estos por distintas alteraciones.

En la actualidad, las actividades de la Biomecánica se pueden extender fundamentalmente en 3 campos: teórico, experimental y computacional. El consiguiente incremento del nivel de salud, así como el elevado coste que supone la experimentación y la imposibilidad de la personalización, han motivado un mayor protagonismo de la Biomecánica desde el punto de vista computacional.

Históricamente, el concepto de adaptación del hueso bajo condiciones mecánicas data, al menos, de 1638 cuando Galileo Galilei señala la implicación mecánica de la forma del hueso (Galilei, 1638).

La hipótesis de Wolff (1892) sugiere que la estructura del hueso se adapta en respuesta a las alteraciones de carga que sufre, de acuerdo a leyes matemáticas (ley de Wolff);o lo que se dado en llamar remodelación ósea.

Muchos son los modelos que se han desarrollado durante los últimos años y se están revisando en la actualidad.^1-11

Fundamentalmente 2 modelos continuos han sido desarrollados los cuales se han impuesto sobre los anteriores; uno desarrollado en la Universidad de Stanford y el otro en la Universidad de Nijmegen. Estos modelos, como fueron originalmente creados comparten muchas características.

El objetivo de este trabajo es implementar el modelo de remodelación ósea propuesto por Jacob (1994), empleando para esto el método de los elementos finitos, logrando implementar el modelo de remodelación anterior mediante una subrutina definida por el usuario (UMAT), esta (UMAT) tiene la capacidad de ser un recurso energético para el analista sofisticado para hacerle frente a las demandas de un modelo material complicado.

En el trabajo por el método de elementos finitos (MEF) de los modelos de remodelación ósea, aparece la dificultad de procesar una gran cantidad de datos, por ejemplo, cómo varia la densidad ósea de cada elemento en el tiempo. Para poder cuantificar estos datos de densidad se acudió a desarrollar, utilizando el Lenguaje programación Visual Fortran, un programa de lectura de los ficheros de resultados obtenidos, para poder brindar una información estadística más compacta que pueda ser analizada de forma rápida por parte de especialistas médicos, haciendo posible el intercambio activo de información entre ingenieros y médicos.

MÉTODOS

El modelo empleado establece una teoría de remodelación dependiente del tiempo, que incluye una condición de remodelación homeostática a nivel local. Se considera que el tejido óseo, para mantener sus características, necesita cierto nivel de estímulo mecánico e intenta siempre autorregularse para conseguir mantener dicho nivel, de modo que si se encuentra sometido a un estado tensional superior modifica sus propiedades mecánicas, incrementándolas, para conseguir reducir ese grado de estímulo mecánico, mientras que cuando el estado tensional es inferior, el hueso disminuye sus características mecánicas con el fin de alcanzar de nuevo ese nivel.

Condición homeostática se puede escribir

Siendo

Y_t:estímulo tensional diario a nivel de tejido.

Y_t^*: Valor de referencia de estímulo tensional a nivel de tejido.

El valor del estímulo mecánico diario puede calcularse como

Siendo N el número de diferentes casos de cargas, es el número promedio de ciclos por día de cada caso de carga n_i, y es la tensión efectiva real. El exponente m es un parámetro que cuantifica la importancia del estado tensional y el número de ciclos, siendo la densidad del hueso cortical con porosidad nula, y la densidad aparente es definida por r

La tensión efectiva es una función del modulo elástico, E, y del valor de la densidad de energía de deformación, U, de acuerdo con la siguiente ecuación.

Al no incluir la direccionalidad ni en las variables del modelo ni en el estímulo, este modelo conduce a un comportamiento isótropo pero no homogéneo, pues en cada punto del sólido existe un valor de densidad diferente y, por tanto, propiedades mecánicas distintas.

La ley de evolución de la densidad viene dada inmediatamente por la siguiente expresión:

Siendo

: la velocidad de remodelación superficial, que cuantifica la cantidad de volumen de hueso generado o eliminado por unidad de superficie disponible y por unidad de tiempo.

: la superficie del hueso disponible para remodelar por unidad de volumen de hueso.

K: el porcentaje de la superficie disponible que se encuentra activo para que se produzca la remodelación.

Después que se conoce la ley de evolución de la densidad, es necesario determinar el valor de las propiedades mecánicas en función de esta; como el hueso es considerado un material isótropo, es suficiente con determinar el módulo de elasticidad y el coeficiente de Poisson. Ello se realiza sobre la base de las siguientes expresiones experimentales: (2,3)

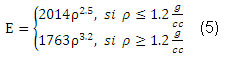
donde el módulo de Young viene dado en MPa.

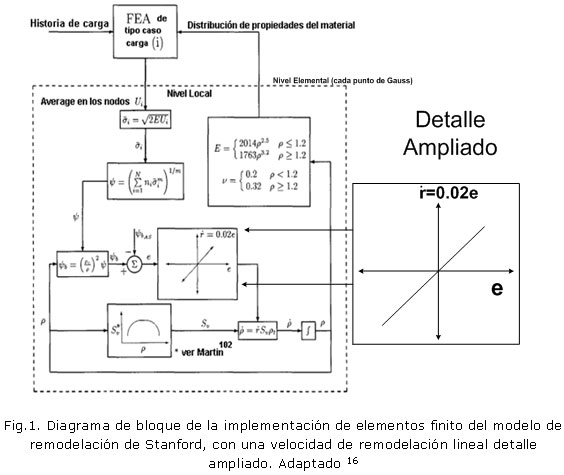
El algoritmo de remodelación de Jacob es mostrado en la figura 1.

MODELO DE ELEMENTOS FINITOS

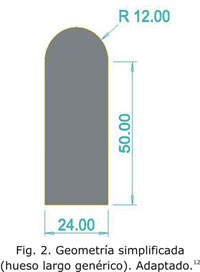
El modelo de elementos finitos fue simplificado a un modelo genérico de hueso largo (Fig. 2.) El modelo contiene 248 elementos bilineales, cuadrilátero de 40 mm de espesor y 282 nodos en un estado de deformación plana.

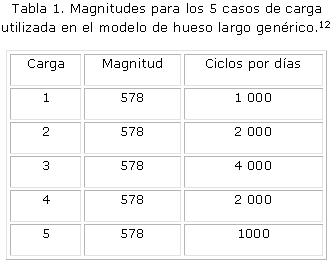
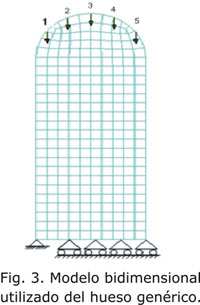
Para caracterizar la historia de carga, se aplican 5 cargas estáticas (tabla 1) en el extremo superior (figura 3) de forma secuencial actuando un número de 10 000 ciclos respectivamente pero con menos frecuencia, como se indica en la figura 4; las cargas se distribuyen en un intervalo de 10 días, aplicando la carga para un caso y descarga para otro caso.

La distribución de la carga se obtiene, haciendo la siguiente relación para distribuir cada caso de carga en el tiempo mostrado (Fig. 3) las cargas se repiten de forma periódica hasta el final del intervalo de tiempo.

La distribución de la carga se obtiene, haciendo la siguiente relación para distribuir cada caso de carga en el tiempo mostrado (Fig. 4) las cargas se repiten de forma periódica hasta el final del intervalo de tiempo

Los parámetros físicos que definen el modelo son los empleados por (¹²):

Las condiciones de frontera impuestas serán la limitación de todos los grados de libertad (empotramiento) en el nodo inferior izquierdo y limitando los demás nodos inferiores un grado de libertad correspondiente a la vertical (figura 3).

Para la solución del modelo se va utilizar el algoritmo requerido para el desarrollo de una subrutina material (modelo constitutivo) implementado dentro de una rutina de FE-código^* en Abaqus/Standard, utilizando el programa de elementos finitos Abaqus v6.4;¹³ como datos adicionales se puede comentar que la solución va a depender de una sola variable de estado (densidad), las variables necesarias para el modelo van a ser las empleadas por Jacob¹² (tabla 2).

RESULTADOS

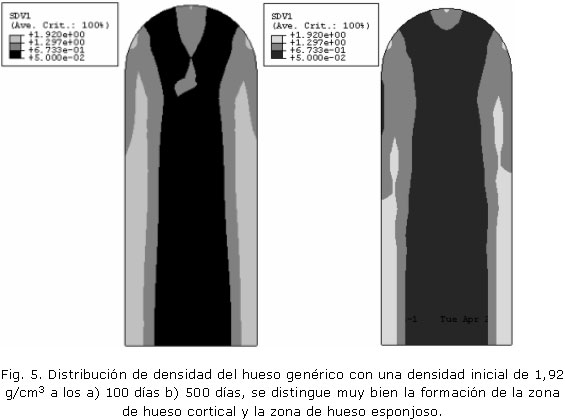
Como se observa en la figura 5, se muestran los resultados obtenidos de la distribución de densidad, en diferentes intervalos de tiempo, partiendo inicialmente de un valor de densidad homogénea igual 1,92 g/cm³, en esta figura se muestra otra distribución de densidad obtenida para un tiempo igual a 500 días, partiendo de una densidad homogénea igual 0,5 g/cm³; nótese que estableciendo una comparación cualitativa entre los dos resultados, siendo los estados iníciales diferentes bajo el mismo estado mecánico, el modelo converge a una distribución de densidades iguales.^14,15

Procesamiento de datos

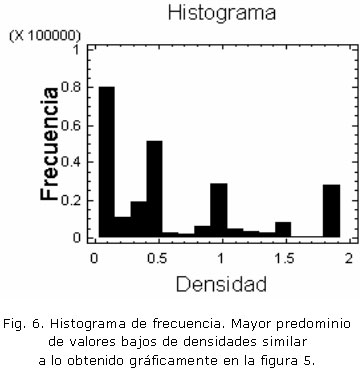
Se puede observar el histograma de frecuencia en la figura 6 y podemos ahora comprobar los resultados visuales en la figura 5, donde se evidencia el mayor predominio de zonas de baja densidad, permitiendo la estimación de una forma cualitativa (4) y cuantitativa (5) de los resultados.

DISCUSIÓN

Un criterio fundamental para evaluar una formulación de remodelación es la habilidad para predecir una distribución de densidad normal cuando es aplicada una historia de carga normal, esta propiedad se observa cuando se comienza una simulación con una distribución de densidad homogénea y se produce la formación de una distribución apropiada en función de la optimización sobre la carga aplicada. Para ello, se comenzó la simulación con una distribución inicial de densidad homogénea y observando cómo evoluciona esta a lo largo del tiempo, hasta adquirir la distribución habitual de densidades; el tipo de simulación utilizada no debe ser considerada realista siempre que las condiciones iniciales sean artificiales, lo cual es nuestro caso.

Se obtuvo similitudes cualitativas en los resultados obtenidos por otros autores^10,12,14,16) correspondiéndose estos con los datos experimentales obtenidos, en términos y zonas de importancia, para la comprobación de la subrutina UMAT implementada.

La implementación de este modelo ha sido utilizada para predecir la remodelación ósea en el fémur con excelentes resultados, de ahí la importancia de contar con este primer modelo desarrollado para trabajos futuros en otras áreas.

Aunque este modelo no se puede tomar como real, sí nos brinda una gran información sobre las densidades habituales. En la figura 5 podemos distinguir lo que sería una estructura típica de un material óseo, en ella se diferencian muy bien la zona cortical y la zona trabecular.

Agradecimientos

Los autores desean agradecer la decisiva colaboración prestada en la realización de este trabajo por parte de profesores de la USP, integrantes del proyecto que se desarrolló con financiamiento de CAPES de Brasil.

REFERENCIAS BIBLIOGRÁFICAS

1. Beaupré GS, Orr TE, Carter DR. An approach for time-dependent bone modeling and remodeling-theoretical development. Journal of Orthopaedic Research. 1990a;8(5):551-651.

2. Beaupré GS, Orr TE, Carter DR. An approach for time-dependent bone modeling and remodeling-application: A preliminary remodeling simulation. Journal of Orthopaedic Research. 1990b;8(5):662-70.

3. Jacobs CR. Numerical simulation of bone adaptation to mechanical loading. [Doctor of Philosophy]: Stanford University; 1994.

4. Carter DR, Fyhrie DP, Whalen RT. Trabecular bone density and loading history: regulation of tissue biology by mechanical energy. Journal Biomechanics. 1987;20:785-95.

5. Prendergast PJ, Taylor D. Prediction of bone adaptation using damage accumulation. Journal [serial on the Internet]. 1994 Date; 27(8).

6. Rodrigues HCJ, Guedes JM, Bendsoe MP, editor. Global and local material optimization models applied to anisotropic bone adaptation. Iutam Symposium-Synthesis in biosolid mechanics; 1998.

7. P. Fernades HR, CRJ. A model of bone adaptation using a global optimisation criterion based on the trajectorial theory of Wolff. Computer methods in Biomechanics and biomedical. Eng. 1998.

8. Fridez P, Terrier A, Rakotomanana L. Three dimensional model of bone external adaptation. Computer methods in Biomechanics and biomedical. Eng. 1997;

9. Mikic D. Carter R. Bone strain gage data an theoretical models of functional adaptation. Journal [serial on the Internet]. 1995 Date; 28(4).

10. Doblaré M. G-AJM. Application of an anisotropic bone-remodeling model based on a damage-repair theory to the analysis of the proximal femur before and after total hip replacement. Journal [serial on the Internet]. 2001 Date; 34.

11. Aznar JMG. Modelos de remodelación ósea: Análisis numérico y aplicaciones al diseño de fijaciones de fracturas del femur proximal [Doctor]. Zaragoza: Centro Politécnico Superior de la Universidad de Zaragoza; 1999.

12. Fischer JK, Jacob CR, Levenston ME, Carter DR. Observation of Convergence and Uniqueness of Node-Based Bone Remodeling Simulations. Journal [serial on the Internet]. 1997 Date [cited Biomechanical Engineering Program, Department of Mechanical Engineering, Stanford University; 25.

13. Hibbitt K, Sorensen. ABAQUS v6.4 User's Manual. Inc. 2002.

14. Cowin SC. Wolff´s law of trabecular architecture at remodeling equilibrium. Journal of Biomechanics Engineering. 1986;108:83-8.

15. Wolff J. The law of bone remodeling. Berlin: Springer-Verlag; 1986.

16. Weinans H, Huiskes R, Grootenboer HJ. The behaviour of adaptative bone remodeling simulation models. Journal [serial on the Internet]. 1992 Date; 25(12).

Recibido: 18 de marzo de 2010.
Aprobado: 9 de junio de 2010.

Ing. Henry Figueredo Losada. Facultad de Mecánica, Grupo de Biomecánica, ISPJAE. Calle 114 e/ 119 y Carretera Toledo, No. 11903, municipio Marianao, La Habana, Cuba. CP 19 300.

^*Código de elementos finitos para definir un modelo constitutivo en Abaqus/Standard (UMAT), el tiempo de integración debe proveer "matriz de rigidez" para formar el jacobiano