Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Cubana de Investigaciones Biomédicas
versión impresa ISSN 0864-0300
Rev Cubana Invest Bioméd vol.30 no.3 Ciudad de la Habana jul.-set. 2011
INGENIERÍA BIOMÉDICA
Algoritmos Genéticos aplicados a la Ingeniería biomédica
Genetic algorithms applied to Biomedical Engineering
Ing. Carlos Galeano Uruena, MSc. Ing. Diego A. Garzón-Alvarado Ph.D, Ing. Juan Miguel Mantilla González, PhD
Departamento de Ingeniería Mecánica y Mecatrónica. Facultad de Ingeniería. Universidad Nacional de Colombia.
RESUMEN
En este trabajo se describe las aplicaciones y alcances del método de los algoritmos genéticos (AG) en la investigación en bioingeniería, mecanobiología y medicina. Para este fin, se ha desarrollado el trabajo sobre tres artículos recientes que describen las aplicaciones de los AG en problemas de ingeniería biomédica. Este trabajo pone de manifiesto la importancia del uso de nuevas metodologías de optimización en las investigaciones biomédicas.
Palabras clave: Simulación, algoritmos genéticos, ingeniería biomédica, optimización.
ABSTRACT
In present paper are described the applications and scope of the genetic algorithms method (GA) in the case of the research in the bioengineering, mechanobiology and medicine. For this aim, the paper on three recent articles was developed describing the applications of the GA in problems related to biomedical engineering. Present paper emphasizes the significance of the use of new methodologies of optimization in the biomedical researches.
Key words: Simulations, genetic algorithms, biomedical engineering, optimization.
INTRODUCCIÓN
Las aplicaciones de los AG en Medicina e Ingeniería biomédica son múltiples. Tan solo en la base de datos de Elsevier, la búsqueda de AG con aplicaciones médicas, pueden alcanzar las 5 000 entradas (mayo de 2011). En este universo de información se pueden encontrar investigaciones en la identificación del cáncer,1 manipulación de imágenes médicas,2 análisis de proteínas,3,4 evaluación de desempeño de fármacos,5 entre otros. En especial, en esta revisión se han elegido tres artículos relacionados con la mecanobiología, es decir, la relación existente entre la biología y la medicina en acción directa con los efectos de las cargas mecánicas sobre los tejidos y órganos. El primer artículo se basa en el desarrollo de modelos de hiperelasticidad en el comportamiento de tejidos blandos, como los músculos, tendones y arterias.6 El desarrollo de los modelos matemáticos que determinan el comportamiento mecánico de un tejido tiene gran relevancia para los ingenieros, en especial, los mecánicos y civiles. El problema consiste en encontrar las constantes que determinan el comportamiento de cada material.
El segundo artículo7 desarrolla un modelo de algoritmos genéticos en el diagnóstico del cáncer de seno. Por último, el tercer artículo desarrolla un modelo para el diseño de andamios estructurales en tejidos lesionados.
Los algoritmos genéticos en el desarrollo de modelos de hiperelasticidad
Una dificultad que tienen los ingenieros en modelar tejidos humanos y animales, es la determinación de la ley constitutiva que rige el comportamiento mecánico del tejido ante fuerzas externas. El problema radica en la identificación de los parámetros del modelo que son requeridos para las leyes hiperelásticas. La búsqueda de los parámetros es, en ocasiones compleja y tediosa, debido a que se requiere un punto inicial para hacer la búsqueda, tal como lo refiere Holzapfel.8 Estos modelos son requeridos en la descripción del comportamiento mecánico de tejidos blandos (o suaves), como la pared arterial del sistema circulatorio.
El proceso de optimización se utiliza para encontrar las constantes del modelo hiperelástico. En este contexto, la función objetivo es la norma del residuo entre la cantidad medida y aquella obtenida mediante la experimentación. Cuando dicha función alcanza un valor cero (o cercano) se obtienen los parámetros del modelo. La norma de la aproximación es un problema convexo, por tanto la solución es única. Esta norma del residuo está dada por:
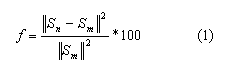
Donde Sn y Sm son los valores de la función a optimizar y la experimental, respectivamente. En particular, la ecuación constitutiva (relación esfuerzo-deformación) tiene dos componentes, uno isotrópico y otro anisotrópico, que corresponde al comportamiento de las fibras. De esta misma forma, la función a optimizar también se puede dividir en dos términos, según la ley constitutiva:
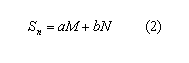
Donde a y b son los parámetros lineales, mientras M y N agrupan los parámetros no lineales a identificar. Al reemplazar (1) en (2) se tiene una función de la forma:
![]() con
con ![]() y
y ![]() .
.
Esto permitirá escribir la función objetivo como una función cuadrática convexa, en términos de x, tal como:
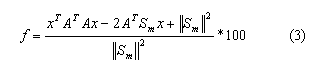
Por tanto, la función objetivo se puede dividir en dos procesos. El proceso analítico y por AG. El primero se pude obtener en función de x, siempre y cuando el gradiente de f sea cero, por lo que se obtiene:
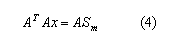
De esta forma, mediante manipulación matemática, se puede encontrar el valor de x.
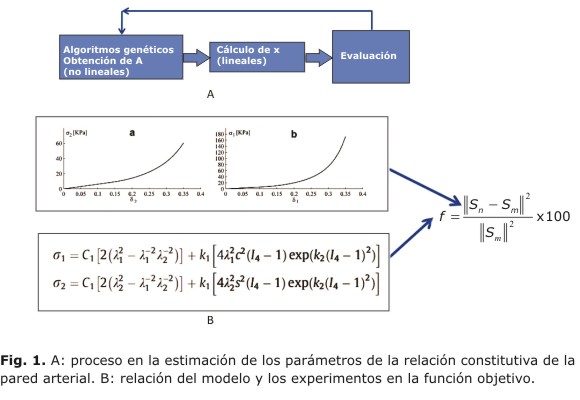
De otro lado, mediante algoritmos genéticos, se deben encontrar los valores no lineales que se encuentran en M y N. El método evita el uso de una única condición inicial, como es tradicional en los métodos clasicos.8 Por tanto, se parte de múltiples puntos semillas (cromosomas/individuos) que forman la población inicial, y van reproduciendo la población mediante operadores de AG (crossover y mutación). Como es común, el proceso se detiene cuando todos los individuos comparten los mismos genes. Gracias a la separación de la parte lineal y la no lineal, los algoritmos genéticos solo son requeridos para los valores no lineales. En la figura 1, en la parte A, se puede observar la metodología propuesta para hallar los valores no lineales que pertenecen a las ecuaciones ![]() y
y ![]() , que se muestran en la parte B de la figura 1. En ésta última, se puede observar la relación entre los experimentos y el modelo matemático propuesto en la función objetivo.
, que se muestran en la parte B de la figura 1. En ésta última, se puede observar la relación entre los experimentos y el modelo matemático propuesto en la función objetivo.
Algoritmos genéticos aplicados en el diagnóstico de cáncer de seno
Tseng y Liao9 proponen una metodología de AG para encontrar la incidencia y relación entre el cáncer/fibroadenoma y los virus existentes en el ADN (DNA virus). Diversos investigadores han desarrollado trabajos similares,10-13 donde se utilizan estrategias de relación entre un marcador molecular y/o genético para detectar el cáncer. Basados en el trabajo de Kim y Han,14 se propone un algoritmo genético de forma tradicional con los tres operadores a saber: selección, crossover (cruzamiento) y mutación. Sin embargo, la diferencia radica en:
1. Cambiar el operador crossover, esto es, el operador crossover actual se sustituye por otro en cualquier tiempo.
2. Ajuste adaptativo de las tasas de crossover y mutación para incrementar la diversidad genética y guía del sistema.
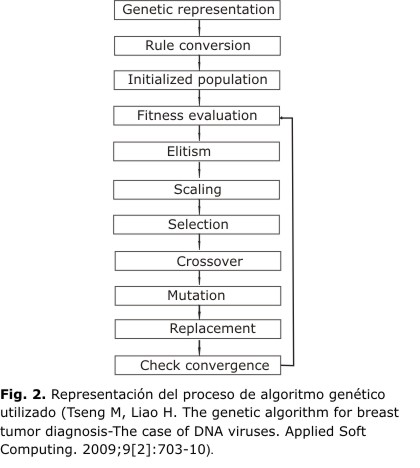
De esta forma, el proceso completo se puede ver en la figura 2.
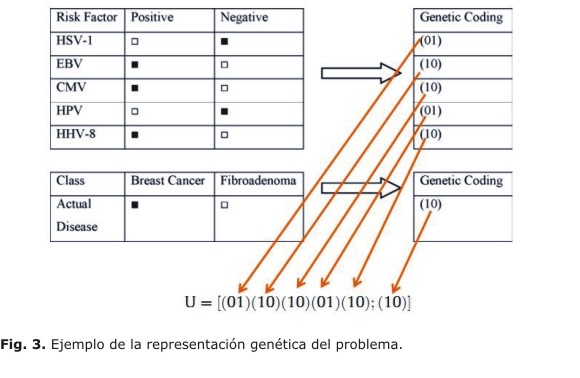
Para determinar la representación genética (del algoritmo) se toman los posibles virus del ADN y la enfermedad de cáncer/fibroadenoma. Por tanto, en el mismo vector se dispone de la incidencia en el factor de riesgo y la enfermedad, separados por un punto y coma, tal como se representa en la figura 3.
Por tanto, el vector U de la figura produce una cadena de factores de riesgo (enlazadas mediante un and o or) que entregan una determinada enfermedad (;=then). Para evaluar la categoría de los datos se ha utilizado una función objetivo de la forma:

De otro lado, al igual que en la naturaleza, los operadores de selección, cruzamiento y mutación son esenciales para aplicar presión a la población para la selección natural. Reglas que tienen un buen fitness, servirán para la reproducción. En este sentido se utilizó la regla de rueda de ruleta.15 El cruzamiento permite intercambiar la información entre diferentes organismos, de igual manera, en este trabajo se empleó cruzamiento de un punto, el cual ocurre en conjunto con la probabilidad, llamada tasa de cruzamiento (0,4 a 0,9). Por último la mutación es utilizada para cambiar, aleatoriamente, un miembro de la población y cambiar un bit en su cadena de representación de bits. Por tanto, la selección y cruzamiento producen nuevas cadenas. En contraposición, la mutación evita alcanzar cualquier punto en el espacio de búsqueda, por tal razón, este valor es manejado con cuidado, con una probabilidad de tasa de mutación de 0,001 a 0,3. Este proceso se repite en 100 generaciones.
Como la rueda de ruleta no garantiza la selección de un individuo particular, se utiliza el individuo de la "elite", para mantenerlo y propagar su descendencia, además de mantenerlo durante varias generaciones. Para este fin, se ha utilizado un operador de elitismo.
Para el entrenamiento y prueba del algoritmo, se utilizaron una fuente de 80 datos, 52 mujeres con cáncer de seno y 28 con fibroadenoma mamario, obtenidos en el Hospital Universitario Chung-Shan.9 En ellas se midieron los virus DNA y mediante ANOVA se estableció la significancia de cada uno de los posibles virus de DNA en la incidencia de Cáncer o fibroadenoma. Se encontraron 5 virus importantes (ver figura 2), de los cuales, el HHV-8 y HSV-1, son los más importantes en la identificación de las enfermedades. Por tanto, mediante el análisis estadístico ANOVA se establecen las características (reglas del modelo) para ser usadas en AG. Por consiguiente, se establecen varias reglas, según el tipo de virus, las cuales se pueden observar en la figura 3. Con 60 datos se alimenta el algoritmo genético para establecer las reglas de desempeño (que fueron 5, según el tipo de virus de ADN) y los 20 datos restantes sirven para probar si el algoritmo ha funcionado correctamente.
En la tabla 1, se observan los resultados, donde en la parte superior están las reglas para la diagnosis del fibroadenoma, y en la parte inferior, para el diagnóstico del cáncer.
Algoritmos genéticos aplicados en el diseño de andamios estructurales para tejidos suaves (scaffolds)
Existe un incremento considerable de lesiones y enfermedades que conducen a la pérdida funcional de tejido blando o duro. Por ejemplo, enfermedades como la osteoporosis desarrolla una pérdida progresiva de tejido óseo confiriéndole a los huesos una alta posibilidad de quebrarse. En este sentido se desarrollan andamios estructurales, denominados scaffolds que tienen la doble intención de, por un lado, permitir el desarrollo de tejido en aquellas zonas con gran pérdida de tejido y, conferir resistencia mecánica por otro. Rezende y otros16 han desarrollado un modelo matemático obtenido experimentalmente que describe el comportamiento mecánico de degradación del material del scaffold. El material utilizado es alginato. De otro lado, para el diseño han utilizado algoritmos genéticos para maximizar el módulo elástico.
Los scaffolds tienen características únicas de alta porosidad (macro-porosidad), apropiada morfología de superficie (micro-porosidad), gran cantidad de área, tamaño de poro adecuado y alta conectividad de la estructura porosa. Además de estas características, el scaffold debe ser biocompatible y biodegradable, como lo es el alginato. Por tanto, el objetivo del artículo16 es encontrar los mejores valores de la cantidad de alginato para su fabricación que maximice el módulo elástico.
El problema de optimización, por consiguiente, se enfoca en determinar las características para la fabricación del scaffold. En especial se deben encontrar los valores óptimos de la composición del alginato y la porosidad inicial, para que, en un tiempo específico, se presente el mayor modulo elástico. Este problema se puede escribir como:
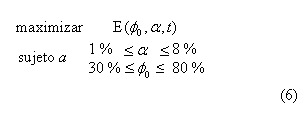
Donde, E es el módulo elástico, a es el porcentaje de alginato y ![]() la porosidad inicial.
la porosidad inicial.
Para conocer la evolución de las propiedades mecánicas en el tiempo, se determinó el cambio de esta en conjunto con la degradación y la porosidad (el cambio en el tiempo se denomina contracción ![]() ). Este paso fue desarrollado mediante experimentación.16 En este sentido, se halla que la evolución de la porosidad en el tiempo es función de la porosidad incial
). Este paso fue desarrollado mediante experimentación.16 En este sentido, se halla que la evolución de la porosidad en el tiempo es función de la porosidad incial ![]() , el porcentaje de alginato a, el término de degradación (o contracción
, el porcentaje de alginato a, el término de degradación (o contracción ![]() ) y las funciones z y y, dado por la expresión:
) y las funciones z y y, dado por la expresión:
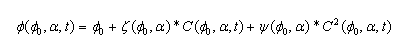 .
.
De igual manera, se puede dar una expresión para el módulo de elasticidad:
![]()
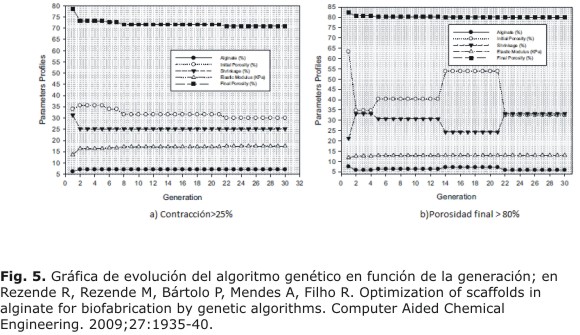
Por tanto, el problema de optimización se amplia para que el nivel de degradación (o contracción) y la porosidad final sean mayor que 25 y 80 %, respectivamente. Para este fin se utilizan los algoritmos genéticos, los cuales inician con poblaciones aleatorias de cromosomas que son un conjunto de soluciones para el problema de optimización original. En cada generación la función objetivo es evaluada en cada individuo y múltiples individuos son estocásticamente elegidos de la población actual (basado sobre el valor del fitness). Luego, son modificadas (recombinadas y mutadas aleatoriamente) para formar una nueva población. El AG termina cuando el número máximo de generaciones se ha producido o, cuando la población entera cumple la función objetivo. El código fue desarrollado en FORTRAN.
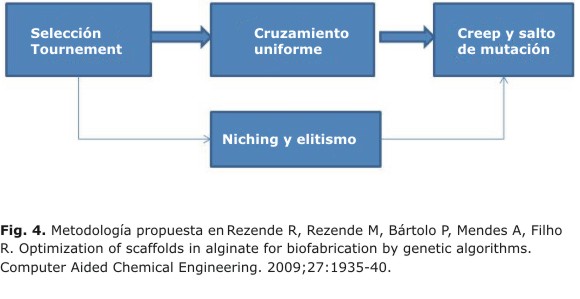
Se han empleado los operadores genéticos de selección del tipo tournament, cruzamiento uniforme, creep y salto de mutación. Además se ha utilizado Niching y elitismo (figura 4).
Los parámetros de entrada del modelo se observan en la tabla 2:
Por tanto, se desarrollaron dos tipos de ejemplos, con contracción mayor al 25 % y porosidad final del 80 %. La figura de la evolución según cada generación se ve en la figura 5.
En este trabajo se llevó a cabo la recopilación de 3 trabajos sobre algoritmos genéticos aplicados a la ingeniería biomédica. Se observa la importancia de los algoritmos en el desarrollo de nuevas teorías sobre el comportamiento de enfermedades y para la optimización de problemas en medicina. En siguientes estudios se desarrollará un algoritmo genético aplicado a problemas de diagnosis en enfermedades ortopédicas.
REFERENCIAS BIBLIOGRÁFICAS
1. Ahmad S, Bergen. S. A genetic algorithm approach to the inverse problem of treatment planning for intensity-modulated radiotherapy. Biomedical Signal Processing and Control. 2010;5(3):189-95.
2. Yeh J, Fu J. A hierarchical genetic algorithm for segmentation of multi-spectral human-brain MRI. Expert Systems with Applications. 2008;34(2):1285-95.
3. Arora V, Bakhshi,A. Theoretical investigations on model ternary polypeptides using genetic algorithm. Some new results. Chemical Physics, In Press. online 15 March 2011.
4. Hill Tobias, Lundgren Andor, Fredriksson Robert, Schiöth Helgi B. Genetic algorithm for large-scale maximum parsimony phylogenetic analysis of proteins. Biochimica et Biophysica Acta (BBA) - General Subjects. 2005;1725(1):19-29.
5. Qiang Fei, Ming Li, Bin Wang, Yanfu Huan, Guodong Feng, Yulin Ren. Analysis of cefalexin with NIR spectrometry coupled to artificial neural networks with modified genetic algorithm for wavelength selection. Chemometrics and Intelligent Laboratory Systems. 2009;97(2):127-31.
6. Harb N, Labed N, Domaszewski M, Peyraut F. A new parameter identification method of soft biological tissue combining genetic algorithm with analytical optimization. Computer Methods in Applied Mechanics and Engineering. 2011;200(1-4):208-15.
7. Tseng, Ming-Hseng, Liao Hung-Chang. The genetic algorithm for breast tumor diagnosis—The case of DNA viruses. Applied Soft Computing. 2009;9(2):703-10.
8. Holzapfel GA. Determination of material models for arterial walls from uniaxial extension tests and histological structure. J. Theor Biol. 2006;238:290-302.
9.Tseng M, Liao H. The genetic algorithm for breast tumor diagnosis—The case of DNA viruses. Applied Soft Computing. 2009;9(2):703-10.
10. Cheng SH, Tsou MH, Liu MC, Jian JJ. Unique features of breast cancer in Taiwan. Breast Cancer Res Treat. 2000;63(3):213-20.
11. Ziegler RG, Hoover RN, Pike MC, Hildesheim A, Nomura AM, West DW, et al. Migration patterns and breast cancer risk in Asian-American women. J Natl Cancer Inst. 1993;85:1819-27.
12. Yu H, Rohan TE, Cook MG, Howe GR, Miller AB. Risk factors for fibroadenoma: a case-control study in Australia. Am J Epidemiol. 1992;135(3):247-59.
13.. Dimmock NJ,. Primrose SB. Carcinogenesis and tumor viruses: introduction to modern virology. 4th ed. London: Blackwell Science Ltd. p. 256-275.
14. Kim MJ, Han I. The discovery of experts' decision rules from qualitative bankruptcy data using genetic algorithms. Expert Syst Appl. 2003;25(4):637-46.
15.Coley DA. An Introduction to Genetic Algorithms for Scientists and Engineers. London: World Scientific; 1998.
16. Rezende R, Rezende M, Bártolo P, Mendes A, Filho R. Optimization of Scaffolds in Alginate for Biofabrication by Genetic Algorithms. Computer Aided Chemical Engineering. 2009;27:1935-40.
Recibido: 5 de febrero de 2011.
Aprobado: 20 de febrero de/ 2011.
Carlos Galeano Truena. Departamento de Ingeniería Mecánica y Mecatrónica. Facultad de Ingeniería. Universidad Nacional de Colombia
Autor para la correspondencia: Diego A. Garzón-Alvarado. Correo electrónico: dagarzona@bt.unal.edu.co