INGENIERÍA BIOMÉDICA

 

Modelo computacional preliminar de la formación de la superficie cerebral

Preliminary computation form of the cerebral surface development

Ing. Angélica Ramírez,^I PhD, Ing. Carlos A. Duque-Daza, PhD,^II Ing. Diego A. Garzón-Alvarado, PhD^II

^I Grupo de Modelado y Métodos Numéricos en Ingeniería (GNUM). Fundación Universidad Central de Colombia.
^II Grupo de Modelado y Métodos Numéricos en Ingeniería (GNUM). Universidad Nacional de Colombia.

 

---

RESUMEN

La corteza cerebral es una lámina gris, formada por cuerpos de neuronas, que cubre los hemisferios cerebrales y cuyo grosor varía de 1,25 mm en el lóbulo occipital a 4 mm en el lóbulo anterior. Debido a los numerosos pliegues que presenta, la superficie cerebral es unas 30 veces mayor que la superficie del cráneo. Estos pliegues forman las circunvoluciones cerebrales, surcos y fisuras y delimitan áreas con funciones determinadas, divididas en cinco lóbulos. La formación de las circunvoluciones puede variar entre individuos y constituyen una característica importante de la formación del cerebro. Estos patrones se pueden representar, de forma matemática, como patrones de Turing. En este artículo se desarrolla un modelo fenomenológico que describe la formación de los patrones de las circunvoluciones que ocurren en la corteza cerebral mediante ecuaciones de reacción difusión con parámetros en el espacio de Turing. Para estudiar la formación de patrones se resuelven varios ejemplos numéricos sobre geometrías simplificadas de un cerebro. Para la solución numérica se utilizó el método de los elementos finitos en conjunto con el método de Newton-Raphson. Los ejemplos numéricos muestran que el modelo puede representar la formación de los pliegues de la corteza cerebral y reproducir patologías de la formación de las circunvoluciones, tales como polimicrogiria y lisencefalia.

Palabras clave: Neocortex, medio continuo, modelos matemáticos.

---

ABSTRACT

Cerebral cortex is a gray layer including neuron bodies covering the cerebral hemispheres and whose thickness fluctuates from 1.25 mm in the occipital lobule to 4 mm in the anterior lobule. Due to the many folds present, la cerebral surface is a thirty times greater than the cranial surface. These folds create the cerebral convolutions, grooves and fissures defining areas with determined functions, divided into five lobules. La convolutions formation may to vary among subjects and are an important characteristic of brain formation. These patterns may be represented in a mathematical way like Turing patterns. The aim of present paper was to design a phenomenological model describing the formation of convolutions patterns occurring in the cerebral cortex by means of diffusion reaction equations with parameters in the Turing space. To study la formation of patterns it is necessary to solve some numerical examples on simplified geometries of a brain. For numerical solution authors used the finite elements method together with the Newton-Raphson method. The numerical examples demonstrate that this model may to represent the folds formation in the cerebral cortex and to reproduce pathologies of the convolutions formation, such as the polymicrogyria and lissencephalous.

Key words: Neocortex, continuous medium, mathematical models.

---

INTRODUCCIÓN

La superficie del cerebro humano posee pliegues, que se denominan surcos, y regiones lisas de la superficie del cerebro que se extienden entre los surcos que se conocen con el nombre de circunvoluciones o gyri.¹ Además, sobre el cerebro se pueden distinguir los lóbulos que corresponden a áreas funcionales diferentes. Se distinguen el lóbulo frontal en la parte anterior del encéfalo, el lóbulo parietal, el lóbulo temporal y el lóbulo occipital en la parte posterior.² Debido a los numerosos pliegues que presenta, la superficie cerebral es unas 30 veces mayor que la superficie del cráneo. Estos pliegues se forman en etapa embrionaria alrededor de la semana 20³ y pueden variar de un individuo a otro.⁴ Adicionalmente, en ocasiones se pueden presentar patologías del desarrollo de la corteza cerebral tales como la polimicrogiria y la lisencefalia.³ La formación de estos patrones de la corteza cerebral se encuentra, aún, en constante debate y estudio médico.^3,5 La completa descripción de la formación de los patrones de la corteza cerebral puede conducir a elucidar patologías de la corteza cerebral y mejorar la calidad de vida de quienes la padecen.

La forma normal del cerebro humano tiene circunvoluciones y surcos bien determinados que permiten un funcionamiento normal de las condiciones motoras y cognitivas de cada individuo.⁴ Entre cada individuo se puede presentar una alta variabilidad de la "forma" de las circunvoluciones manteniendo un límite fisiológico.⁵ Fuera de estos límites de forma, se presentan enfermedades como la polimicrogiria que es una malformación cerebral caracterizada por excesivos pliegues corticales y surcos poco profundos.⁶ También se puede presentar la lisencefalia, que es un trastorno poco común de la formación del cerebro caracterizado por microcefalia y agiria, que es una ausencia de las circunvoluciones o gyri (pliegues) normales del cerebro.⁷

La naturaleza de la aparición de la forma de la corteza cerebral es un tema en constante investigación que implica el trabajo de médicos, físicos, matemáticos e ingenieros para elucidar la formación de los patrones corticales. La investigación en esta área puede clasificarse desde dos aspectos fundamentales: mecánico y bioquímico. Desde el punto de vista mecánico, en W Le Gros Clark⁸ se muestra que la formación de las circunvoluciones se presenta gracias a la expansión de la superficie cortical que se ve restringida por el cráneo y los ganglios basales. De igual forma, en Richman D y otros⁹ se muestra que el crecimiento diferencial de la corteza cerebral causa las circunvoluciones. Aquel artículo también explica que las patologías de la formación del neocortex se presentan gracias a cambios en las propiedades mecánicas del tejido cerebral. Adicionalmente, en Toro R y otros¹⁰ se muestra que la formación de la corteza se presenta por la anisotropía en las propiedades mecánicas del tejido de la corteza cerebral.¹¹

Desde el punto de vista bioquímico, se han desarrollado otras hipótesis que conducen a la formación de los pliegues cerebrales. En Lefevre J y otros³ se desarrollan las condiciones necesarias para que un sistema de reacción-difusión difusión genere los patrones necesarios para la formación de las circunvoluciones corticales. En aquel artículo se supone que el sistema reactivo de Gray-Scott puede determinar la formación de la corteza cerebral. Por su parte, en Cartwright J¹² se muestra la semejanza que existe entre los patrones de Turing en forma de laberinto y el desarrollo de la corteza cerebral. En aquel artículo utilizan las ecuaciones de Van Der Pol-FitzHughNagumo como el sistema reactivo gobernante y se resuelve el problema de reacción difusión en 2D. De igual manera en P Rakic¹¹ se muestra que la formación de los patrones de las circunvoluciones corticales se presenta por el control genético intrínseco durante la formación del cerebro. Las hipótesis de estos artículos están apoyadas en recientes descubrimientos en los campos de la genética y la bioquímica. En Chenn A¹³ se muestra que la corteza cerebral de los ratones transgénicos que tienen una forma alterada de la proteína catenina -b se expande horizontalmente en área, pero no en espesor.

Con base en el artículo de Chenn A se puede suponer que la catenina -b es un precursor activador de la formación de las circunvoluciones de la corteza cerebral y que, asociada a esta molécula, se presenta un inhibidor que completa el sistema reactivo. Las dos moléculas forman unos sistemas reacción-difusión que forman patrones altamente estables en el tiempo e inestables en el espacio similar a los patrones de Turing.^3,13 Por esta razón la hipótesis inicial de este artículo se basa en el supuesto de que los agentes bioquímicos son los principales responsables en la conformación de la corteza cerebral en animales superiores, especialmente, en humanos.

Siguiendo un planteamiento similar al utilizado en Lefevre J,³ y Cartwright J,¹² se utiliza el modelo de reacción de Glucólisis, con parámetros en el espacio de Turing, para simular la aparición de los patrones de la corteza cerebral. Para la solución de las ecuaciones de reacción difusión se presenta un método de solución en superficies en 3 dimensiones mediante el método de los elementos finitos bajo el uso de la formulación lagrangiana total. Se simularon varios casos: a) formación normal de patrones, b) formación de patologías asociadas al desarrollo, c) microgiria y d) lisencefalia.

MÉTODOS

Sistema de reacción-difusión (RD)

Siguiendo el enfoque bioquímico, se puede suponer que un sistema de reacción difusión puede controlar la formación de los patrones que se presentan en la corteza cerebral. Para este fin se define un sistema de Reacción difusión, para dos especies, dado por (1):

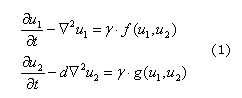
Donde u₁ y u₂ son las concentraciones de las especies químicas presentes en los términos de reacción, f y g, d es el coeficiente de difusión adimensional y g es una constante de adimensionalización del sistema.¹³ Se debe recordar que u₁ y u₂ pueden ser catenina -b y su activador (o inhibidor),¹³ respectivamente. También se puede suponer que un conjunto de morfogenes (como por ejemplo: Pax6, Ngn2, Id4³) altamente acoplados pueden guiar la formación de los patrones de las circunvoluciones de la corteza cerebral.

Los sistemas RD han sido estudiados ampliamente para determinar su comportamiento en diferentes escenarios de parámetros^13,14 geométricos^14,15 y para diferentes aplicaciones biológicas.^16-18 Una de las áreas en que se ha desarrollado gran trabajo sobre las ecuaciones RD es la formación de patrones que son estables en el tiempo e inestables en el espacio.^19,20 En especial, Turing²¹ en su libro "Thechemicalbasis of morphogenesis" desarrolló las condiciones necesarias para la formación de patrones espaciales. Las condiciones para la formación de patrones determinan el espacio de Turing dado por las siguientes restricciones (2):

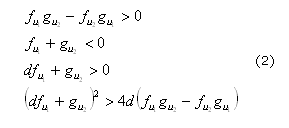
Donde f₁ y g₂ indican las derivadas de las funciones de reacción con respecto a las variables de concentración, por ejemplo:²²

Estas restricciones están evaluadas en el punto de equilibrio que se obtiene haciendo:

Las ecuaciones (1) y sus restricciones (2) permitieron el desarrollo de una rama de investigación de los sistemas dinámicos:¹⁹ las Inestabilidades de Turing. La teoría acerca de los patrones de Turing ha permitido explicar la formación de patrones biológicamente complejos, como las manchas que se encuentran en la piel de algunos animales^16,17 y en problemas de morfogénesis,¹⁹ entre otros. Además, recientemente se ha comprobado, experimentalmente, que el comportamiento de algunos sistemas RD generan patrones de ondas viajeras y patrones espaciales estables.^23-25

La ecuación (1) contiene términos reactivos (f(u₁,u₂) y g(u₁,u₂)) que tienen una importante contribución en la formación de los patrones de Turing. Por ejemplo, en Lefevre J³ y Cartwright J¹² se han utilizado los modelos de Gray-Scott y de Van Der Pol-FitzHughNagumo, respectivamente, para simular la formación de la corteza cerebral. Similar a estas ecuaciones del tipo activador-inhibidor, se pueden utilizar las ecuaciones de reacción de Bruselador o Glucólisis, como se describe en Garzón D.²²

En este artículo, las ecuaciones utilizadas para predecir la formación de patrones son las de glucólisis²⁶ dadas por:

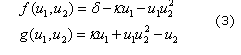
Donde d, k, a y b son parámetros adimensionales del modelo. Los puntos de estado estable están dados por:

Aplicando las restricciones (2) al modelo (3) en el punto de estado estable (u_1,u)₀ se obtiene un conjunto de restricciones que permiten establecer el sitio geométrico de los parámetros en el espacio de Turing.²²

Deformación de la corteza cerebral: circunvoluciones

Para deformar la corteza cerebral durante el desarrollo se utilizaron las ideas sugeridas en Lefevre J,³ Harrison L,²⁶ y Holloway D,²⁷ donde la superficie se deforma en función de las sustancias (morfogen) presentes en el dominio. Esto es, la superficie S, se deforma en función de su normal N y de la cantidad de activador existente en cada punto material, por tanto:

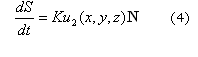
Donde K es una constante que determina la tasa de crecimiento.

Al incluirse el término de crecimiento de la superficie (ecuación 4), se modifican las ecuaciones (1), donde se presenta un nuevo término que tiene en cuenta la convección y la dilatación del dominio dado por:

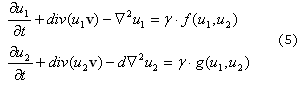
Donde el término nuevo div(u₁,v) incluye la convección y dilatación que se debe al crecimiento del dominio, dado por la velocidad:

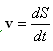
Para solucionar el sistema de reacción difusión convección descrito en (5) se utiliza el método de los elementos finitos²⁸ y el método de Newton-Raphson²⁹ para solucionar el sistema no lineal de Ecuaciones diferenciales parciales que se derive de la formulación. La imposición del campo de crecimiento de los patrones de la superficie cerebral, se hace mediante la solución de la ecuación (4), con lo que se obtiene la nueva configuración (actual) y el campo de velocidades que se incluirá en el problema de RD.

En primer lugar se muestra la solución de las ecuaciones de reacción difusión mediante el método de los elementos finitos.

Solución del sistema de reacción-convección-difusión

La formulación del sistema RD incluyendo el transporte convectivo se puede escribir como (6)²²

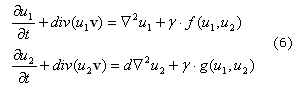
Donde u₁ y u₂ son las variables químicas del sistema de reacción difusión. Esta ecuación también se puede escribir en términos de la derivada total (7).²²

Donde se debe tener en cuenta que:^30,31

Estas ecuaciones se han resuelto mediante el método de los elementos finitos.³¹ El programa que lo resuelve fue desarrollado en FORTRAN y los resultados han sido posteriormente procesados en TECPLOT para su visualización.

Aplicación del campo de velocidades

Para calcular el movimiento de la malla y la velocidad a la cual se deforma el dominio se utiliza la ecuación (4), la cual se integra mediante el método de Euler, dado por:²⁹

Donde S_t+dt y S_t son la configuración de la superficie en el estado t y t+dt. Por tanto la velocidad se obtiene mediante (9):

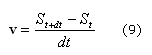
Donde el término de velocidad tiene dirección y magnitud que depende del punto material de la superficie S.

Aspectos de la implementación computacional

Para implementar el modelo de reacción-difusión en elementos finitos se utiliza la formulación antesdescrita. Es importante anotar que, aunque la superficie se encuentra orientada en el espacio 3D, los cálculos numéricos se hacen en 2D. Para este objetivo, se encuentra la normal a cada elemento (Z') y se ubican los ejes primos (X'Y') formando un plano paralelo al plano del elemento. Para enmallar la geometría se utilizan elementos triangulares de primer orden con tres nodos. Por tanto, el cálculo se simplifica pasando de un sistema 3D a un sistema bidimensional donde se soluciona los modelos de reacción-difusión en cada instante de tiempo. La relación existente entre los ejes X'Y'Z' y XYZ se puede obtener mediante una matriz de transformación T.³⁰

Para solucionar el sistema de ecuaciones resultantes del método de los elementos finitos con el método de Newton-Raphson se hizo un programa en FORTRAN y se solucionaron los siguientes ejemplos en un Laptop de 4096 MB en RAM y 800 MHz de velocidad de procesador.

Ejemplos de aplicación y resultados numéricos

El primer ejemplo numérico se desarrolla para la formación normal del cerebro en etapa fetal. Para este objetivo se utiliza una geometría simplificada de la superficie de una esfera. La figura se enmalla con 49 446 elementos triangulares y 24 725 nodos (Figura 2a). Los parámetros adimensionales del sistema de reacción difusión de glucólisis están dados por d = 0,08, d = 1,2 y k = 0,06. Por tanto el estado estable está dado en el punto de equilibrio (u_1,u)₀=(0,8,1,2), de tal manera que las condiciones iniciales son aleatorias alrededor del estado estable.²² Para todas las simulaciones se ha utilizado K = 0,05 en las ecuaciones (4) y (8).

En la figura 1a se observa la evolución de la circunvoluciones del cerebro en t = 3200. Obsérvese la formación de laberintos y puntos ciegos de circunvoluciones que se aproxima a la forma del cerebro (fig. 1b). El patrón obtenido está dado por bandas de alta concentración de una de las especies químicas, por lo cual el dominio ha crecido en dirección normal a la superficie y por tanto han generado los surcos y las cisuras propias de la corteza cerebral.

Se observa en la figura 2 una simulación con las mismas características geométricas y de malla que en el caso anterior. Sin embargo, los parámetros adimensionales utilizados son d = 0,0125, d = 2,8 y k = 0,06. Por tanto el estado estable está dado en el punto de equilibrio (u_1,u)₀ = (0,35,2,8). En este caso los resultados de la simulación generan patrones en forma de puntos con poco espacio entre sí. Obsérvese que toda la superficie contiene estos puntos y gracias a la ecuación de crecimiento de las circunvoluciones dada en (4) se deforma el dominio en dirección normal produciendo una gran cantidad de circunvoluciones pequeñas y redondas, lo que recuerda a la patología de polimicrogiria. En la figura 2c) se muestra la patología que tiene alta concordancia con los resultados finales de la simulación (ver figura 2b).

En la figura 3 se muestran los resultados obtenidos sobre una geometría con las mismas condiciones que las anteriores. Se utilizan los parámetros (para el modelo de glucólisis) d = 0,8, d = 1,2 y k = 0,06 y cuyo punto de estado estable es:

En este caso el resultado es semejante al de una corteza cerebral con un alto grado de lisencefalia, donde se forman surcos altamente espaciados y puntos ciegos lejanos. Es importante notar la semejanza con el primer ejemplo, sin embargo, en este caso los surcos son más espaciados debido al aumento de la difusión d. Nuevamente se estabiliza el sistema en t = 3 200 (adimensional) (figura 3).

CONCLUSIONES

En este artículo se ha presentado un modelo fenomenológico a partir de ecuaciones de reacción difusión para predecir la formación de las circunvoluciones presentes en el cerebro. La aplicación de los modelos de reacción difusión con parámetros en el espacio de Turing es un área de constante trabajo y controversia en la biología^32,33 y que ha despertado un reciente interés gracias al trabajo de Sick y otros,³³ donde se confirma la validez de las ecuaciones de reacción difusión en un modelo sobre la aparición del folículo de cabello. Desde este punto de vista, el trabajo desarrollado en este artículo ilustra la validez de las ecuaciones de reacción difusión para representar patrones biológicos complejos, como son los patrones que se forman en la corteza cerebral.

De este trabajo se puede especular acerca de la existencia de un sistema reactivo (activador-inhibidor) en la superficie del cerebro que puede dar una explicación para los patrones hallados. Adicionalmente, se puede explicar la alta estabilidad de la aparición de los patrones. Esto es, la repetitividad de los patrones se debe a un sistema bioquímico especializado que permite la formación de los surcos y circunvoluciones. Por tanto se confirman los hallazgos de otros trabajos²² que establecen que los patrones son altamente estables en el tiempo y repetibles bajo ciertas características geométricas, siempre que los parámetros del sistema reactivo se encuentren en el espacio de Turing. De igual manera los patrones son repetibles ante diversas condiciones iniciales.^13,22

Para probar esta hipótesis se ha programado la formulación de un sistema de ecuaciones de reacción-difusión bajo la acción de la deformación del dominio. Para este objetivo se utilizó la mecánica de medio continuo con lo cual se llega a la forma general de las ecuaciones de reacción difusión en 2 y 3 dimensiones sobre dominios que presentan deformación. Las ecuaciones resultantes son similares a las mostradas en Madzvamuse A,³⁴ donde se llevan a cabo simplificaciones importantes sobre el campo de dilatación. A partir de las ecuaciones de reacción-difusión bajo la acción de dominios crecientes se lleva a cabo una formulación lagrangiana total. El sistema de reacción difusión se soluciona mediante el método de los elementos finitos, utilizando un enfoque de Newton-Raphson para solucionar el problema no lineal. Esto permite utilizar pasos de tiempo más largos y obtener soluciones más próximas a la real.

Se debe tener en cuenta que los resultados obtenidos con el modelo matemático de reacción difusión están basados en suposiciones y simplificaciones que deben ser discutidas.

El modelo se basa en la suposición de un sistema bioquímico altamente acoplado (de forma no lineal) entre un activador y un inhibidor que generan patrones de Turing. Recientemente se ha comprobado la existencia de un activador de la formación de las circunvoluciones cerebrales denominado catenina-b.¹³ Adicionalmente se han hallado otra cantidad de moléculas que pueden ser responsables del desarrollo de la corteza cerebral, como son Pax6, Ngn2, Id4.³ Sin embargo, la suposición de la existencia de un sistema bioquímico altamente acoplado no se ha comprobado experimentalmente, por lo cual el modelo es una hipótesis que debe ser comprobada en futuras investigaciones. Además, es factible, al igual que en otros modelos biológicos (ver Garzón-Alvarado GA y otros),³⁵ que estén involucrados un gran número de factores químicos (morfogenes) que interactúen para formar los patrones superficiales que se encuentran en la corteza cerebral. Un punto importante en el desarrollo del cerebro es la interacción del sistema bioquímico con factores mecánicos propios del crecimiento del cerebro.

A pesar de las limitaciones antes descritas, el modelo y las suposiciones de que las ecuaciones de reacción difusión rigen la aparición de los patrones superficiales del cerebro, son una buena aproximación cualitativa cercana a la realidad, como se observa en los resultados obtenidos. Por tanto, este artículo deja abierta la discusión acerca del alcance teórico de la propuesta y la posibilidad de contrastar los resultados aquí consignados con experimentación. En trabajos futuros se abordará el problema del efecto del crecimiento en la formación de la corteza cerebral y el efecto de la deformación mecánica en estos patrones.

REFERENCIAS BIBLIOGRÁFICAS

1. Pocock Gillian, Richards Christopher D. Human Physiology: The Basis of Medicine, 3rd ed. Oxford Core Texts; 2006.

2. Dufour R, Delamarche A, Multon, Perlemuter L. Anatomie, physiologie, biomécanique en STAPS. París: Editions Masson; 2002.

3. Lefevre J, Mangin J. A Reaction-Diffusion Model of human Brain Development. PLOS Computational Biology. 2010;6(4):1-10.

4. Gannong W. Review of Medical Physiology. LANGE Basic Science. Nueva York: Ed. Mc Graw Hill, 2005.

5. Regis J, Mangin J, Ochiai T, Frouin V, Riviere D, et al. «Sulcal Root'' Generic Model: a Hypothesis to Overcome the Variability of the Human Cortex Folding Patterns. Neurologia medico-chirurgica. 2005;45:1-17,

6. Ropper A, Samuels M. Adams V. Principles of Neurology, 9th ed. Nueva York: Mc Graw Hill; 2005.

7. Mota V, Valdivieso O, Quiroz L, Criales J. Lisencefalia. Gac Méd. 2005;141(5):441-2.

8. W Le Gros Clark. Deformation patterns in the cerebral cortex. Essays on Growth and Form; 1945. p. 1-22.

9. Richman D, Stewart R, Hutchinson J, Caviness Jr. V. Mechanical Model of Brain Convolutional Development. Science. 1975;189:18-21.

10. Toro R, Burnod Y. A Morphogenetic Model for the Development of Cortical Convolutions. Cerebral Cortex. 2005;15:1900-13.

11. P Rakic. Neuroscience: genetic control of cortical convolutions. Science Signaling. 2004;303:1983.

12. Cartwright J. Labyrinthine Turing Pattern Formation in the Cerebral Cortex. Journal of Theoretical Biology. 2002;217:97-103.

13. Chenn A, Walsh C. Regulation of Cerebral Cortical Size by Control of Cell Cycle Exit in Neural Precursors. Science. 2002;297(5580):365-9.

14. Meinhardt H. Models of Biological Pattern Formation. New York: Academic Press; 1982.

15. Madzvamuse A. Time-stepping schemes for moving grid finite elements applied to reaction-diffusion systems on fixed and growing domains. J Comp Phys. 2005;24(1): 239-63.

16. Madzvamuse A, Sekimura T, Thomas RDK, Wathen AJ, Maini PK. A moving grid finite element method for the study of spatial pattern formation in Biological problems. In: Noji S, Nueno N, Maini PK, Sekimura T. Morphogenesis and Pattern Formation in Biological Systems Experiments and Models. Tokyo: Ed. Springer-Verlag; 2003. p. 59-65.

17. Madzvamuse A, Maini PK, Wathen AJ. A moving grid finite element method applied to a model biological pattern generator. J Comp Phys. 2003;190:478-500.

18. Madzvamuse A, Thomas RDK, Maini PK, Wathen AJ. A numerical approach to the study of spatial pattern formation in the ligaments of arcoid bivalves, Bull. Math Biol. 2002;64:501-30.

19. Meinhardt A, Geirer and H. A theory of biological pattern formation. Kybernetik. 1972;12(17):30-9.

20. Chaplain M, Ganesh AJ, Graham IG. Spatio-temporal pattern formation on spherical surfaces: Numerical simulation and application to solid tumor growth. J Math Biol. 2001;42:387-423, .

21. Turing A. The chemical basis of morphogenesis. Phil Trans R Soc.1952;237:37-72.

22. Garzón D. Simulación de procesos de reacción-difusión: Aplicación a la morfogénesis del tejido óseo [Ph.D. Thesis]. Universidad de Zaragoza, Zaragoza, España; 2007.

23. Wit A De. Spatial patterns and spatiotemporal dynamics in chemical systems. Adv Chem Phys. 1999;109: 435-513.

24. Maini PK, Painter KJ, Chau HNP. Spatial pattern formation in chemical and biological systems. J Chem Soc Faraday Trans. 1997:93:3601-10.

25. Showalter R, Kapral and K. Chemical Waves and Patterns. Kluwer;1995.

26. Harrison L, Wehner S, Holloway D. Complex morphogenesis of surfaces:theory and experiment on coupling of reaction-diffusion patterning to growth. Faraday Discussions. 2002;120:277-93.

27. Holloway D, Harrison L. Pattern selection in plants: Coupling chemical dynamics to surface growth in three dimensions. Annals of Botany. 2008;101(361).

28. Hughes TJR. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis. Courier Dover Publications; 2003.

29. Hoffman J. Numerical Methods for Engineers and Scientists. Nueva York: McGraw Hill; 1992.

30. Holzapfel G A. Nonlinear solid mechanics. John Wiley; 2000.

31. Belytschko T, Liu WK, Moran B. Nonlinear Finite Elements for Continua and Structures. West Sussex:John Wiley and Sons; 2000.

32. Maini EJ, Crampin PK. Reactiondiffusion models for biological pattern formation Meth Appl Anal. 2001;8(3):415-28.

33. Sick S, Reinker S, Timmer J, Schlake T. WNT and DKK determine hair follicle spacing through a reactiondiffusion mechanism. Science. 2006;314:1447-50.

34. Madzvamuse Anotida, Maini Philip K. Velocity-induced numerical solutions of reaction-diffusion systems on continuously growing domains. Journal of Computational Physics. 2007;225(1):100-19.

35. Garzón-Alvarado GA, García-Aznar JM, Doblaré M. Appearance and location of secondary ossification centres may be explained by a reactiondiffusion mechanism. Comput Biol Med. 2009;39:554-61.

Recibido: 1ro. de marzo de 2011.
Aprobado: 17 de marzo de 2011.

Ing. Angélica María Ramírez Martínez Ph.D. Fundación Universidad Central de Colombia.

Autor para la correspondencia: Diego A. Garzón-Alvarado. Correo electrónico: [e-mail]