INGENIERÍA BIOMÉDICA

 

Comportamiento fractal espacial en la expansión de la distribución del flujo sanguíneo cerebral en Alzheimer

Spatial fractal behavior in the lengthening of cerebral bloodstream distribution in Alzheimer disease

Ing. Andy Domínguez Monterroza, Ing. Diego Garzón-Alvarado Ph.D

Universidad Nacional de Colombia.

---

RESUMEN

El Alzheimer es una enfermedad neurodegenerativa que afecta a millones de personas alrededor del mundo. Las causas de esta aún son desconocidas. La geometría fractal es una teoría matemática que permite medir objetivamente la irregularidad de los objetos o procesos naturales; las estructuras y los comportamientos fisiológicos del cuerpo humano se pueden caracterizar matemáticamente a través de la dimensión fractal, la cual mide el grado de irregularidad o complejidad del fractal. La distribución del flujo sanguíneo cerebral en Alzheimer es notablemente irregular, por ello la dimensión fractal es una medida objetiva, la cual suponemos, cuantifica esta distribución. El coeficiente de expansión fractal se define para aquellos objetos dinámicos que poseen dimensión fractal y estima la expansión del fractal sobre su espacio circundante. Este coeficiente se asocia con el grado de conectividad que pueda poseer el fractal para expandirse. En el presente trabajo se determinaron los coeficientes de expansión fractal para la distribución del flujo sanguíneo cerebral en 21 pacientes con Alzheimer y en 11 sujetos normales en las zonas cerebrales posterior y anterior (tomados de la literatura). Los valores de los coeficientes resultaron ser mayores en Alzheimer respecto a los normales en las dos zonas, valores comparados respecto al espacio circundante en que sucede la expansión. Esto último sugiere el comportamiento de las conexiones neuronales en las zonas evaluadas.

Palabras clave: Fractal, coeficiente de expansión fractal, Alzheimer, demencia, flujo sanguíneo.

---

ABSTRACT

Alzheimer disease is a neurodegenerative process affecting millions of persons at world scale. Even nowadays its causes are unknown. The fractal geometry is a mathematical theory allows to measure objectively the irregularity of objects or the natural processes; structures and physiologic behaviors of human body may be in a mathematical way be characterized through the fractal dimension, which to measure the irregularity or complexity degree of fractal. Distribution of cerebral blood flow in Alzheimer's disease is very irregular, thus the fractal dimension is an objective measure, which supposedly to quantify this distribution. The fractal expansion coefficient is defined for those dynamic objects having fractal dimension and estimates the fractal expansion on its surrounding space. This coefficient is associated with the connection that may to has the fractal for its expansion. The objective of present paperwas to determine the fractal expansion coefficients for the cerebral blood flow distribution in 21 patients presenting with Alzheimer's disease and in 11 normal subjects in the posterior and anterior cerebral zones, compared values regarding the surrounding space where expansion occur. This latter suggest the behavior of neuronal connections in assessed zones.

Key words: Fractal, expansion fractal coefficient , Alzheimer, dementia, cerebral blood flow (CBF), blood flow.

---

INTRODUCCIÓN

El Alzheimer es una enfermedad degenerativa de las células nerviosas de la corteza cerebral, la cual progresivamente manifiesta un deterioro global en los procesos cognitivos y de comportamiento; afecta la memoria y la capacidad para aprender, razonar, comunicar y en el desempeño normal de ciertas actividades cotidianas.¹ Este desorden neurológico afecta a millones de personas. Según el último reporte mundial de Alzheimer 2009² se estima que 35,6 millones de personas a lo largo del mundo padecerán la enfermedad en el año 2010, duplicándose esta cifra en 20 años a 65,7 millones de personas para el 2030. Además se estima que el 10 % de los individuos mayores a 65 años de edad y el 50 % de las personas mayores a 85 años de edad son los más afectados.³

Las causas del Alzheimer son aún desconocidas, por ello las investigaciones que actualmente se adelantan en torno a la naturaleza de esta, como la de otros trastornos neuronales, son multidisciplinarias; en ellas convergen un sinnúmero de disciplinas que abarcan desde la genética y bionformática,^4-7 hasta llegar al campo teórico de la física y la matemática.^8-10

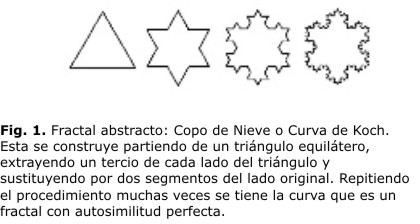
De otro lado, la Geometría Fractal permite caracterizar y describir objetivamente estructuras y procesos que ocurren en la naturaleza. Fue Benoit Mandelbrot en el año de 1977 quien introdujo el término fractal para referirse a objetos que presentan un alto grado de irregularidad en su forma y, una autosimilitud bajo muchas escalas de observación. Los fractales pueden ser abstractos o matemáticos y salvajes o naturales. Los abstractos son objetos matemáticos en los cuales la autosimilitud se presenta como perfecta, tal es el caso de la curva de Koch (figura 1), mientras que los salvajes son objetos naturales en los cuales la autosimilitud se presenta estadísticamente, es decir, el fractal es aproximadamente autosimiliar a diferentes escalas; las propiedades estadísticas de la parte son proporcionales con las propiedades estadísticas del todo.^11,12

En la naturaleza muchos fractales exhiben autosimilutud estadística: los árboles, nubes, montañas, cristales de agua, la estructura de la galaxia, y en el cuerpo humano, ejemplos de tal autosimilitud, también se han hallado en las neuronas y en el flujo sanguíneo regional (figuras 2 y 3). Por extensión un fractal se refiere a aquellos objetos o sistemas que exhiben una irregularidad y complejidad, sea en su forma y/o en su comportamiento.

De este concepto se derivó que la medida numérica adimensional que caracteriza de una mejor manera las estructuras de formas irregulares es la dimensión fractal. Las estructuras del cuerpo humano así como muchos de los procesos fisiológicos, tal como el flujo sanguíneo regional, que acontecen en este, son irregulares, complejas, en su forma y dinámica (la vermis del cerebelo, la vasculatura pulmonar, la frecuencia diaria cardiaca).^13-15 Se ha observado que el flujo sanguíneo regional en órganos y tejidos, es eminentemente complejo (irregular), pudiéndose obtener importantes resultados en la aplicación del análisis fractal en el corazón,^16,17 en los pulmones,^18,19 en el tejido músculo esquelético.²⁰

En la enfermedad Alzheimer, gracias a diferentes tipos de técnicas de neuroimagen, muestran que el flujo sanguíneo cerebral es altamente heterogéneo, irregular, por lo que los conceptos de la geometría fractal han resultado útiles al extenderse en el estudio de este flujo en la enfermedad.^21-23 En estos últimos estudios la dimensión fractal es un índice que da cuenta del grado de heterogeneidad (irregularidad) del CBF (por sus siglas en inglés: cerebral blood flow).

Nagao y otros,²¹ mediante un análisis fractal tridimensional sobre imágenes obtenidas a través de SPECT (del inglés: Single Photon Emission Computed Tomography) en las zonas posterior y anterior del cerebro, cuantificó la distribución del flujo sanguíneo cerebral CBF en pacientes con Alzheimer y en sujetos que no la padecen, obteniendo diferencias matemáticas en las dimensiones fractales halladas, lo cual es un índice matemático que caracteriza la heterogeneidad (irregularidad) del CBF entre estas poblaciones.

Por otro lado, el coeficiente de expansión fractal es una relación matemática que permite aproximarse a la evolución espacial de la complejidad del sistema objeto de estudio. El coeficiente de expansión fractal es una medición matemática que se define para aquellos objetos dinámicos que presentan dimensión fractal y que presentan crecimiento o expansión en un dominio espacial determinado: relaciona la dimensión fractal del objeto respecto al espacio euclidiano más próximo en el cual sucede la expansión.²⁴ Este coeficiente se ha hallado en poblaciones celulares (coeficiente de expansión fractal celular),²⁴ se han obtenido importantes relaciones con la conectividad del objeto o proceso dinámico estudiado. Dado que esta derivación matemática es objetiva, por tratarse de conceptos holísticos de sistemas complejos, es reproducible a otros sistemas que exhiban dinámica compleja subyacente.

De acuerdo a esto último y partiendo de las dimensiones fractales halladas por Nagao y otros²¹ en 21 pacientes con Alzheimer y en 11 sujetos normales, y de acuerdo con la derivación matemática de Waliszewski y Konarski,²⁴ se propone determinar los coeficientes de expansión fractal para estas poblaciones. Estos coeficientes cuantifican la expansión del CBF en el espacio circundante en que se distribuye este mismo. Además que estos valores sugieren el grado de conectividad de la zona en que acontece la expansión en personas que padecen Alzheimer y en sujetos normales. Este es el primer trabajo en estimar los coeficientes de expansión fractal en la distribución del CBF en sujetos con Alzheimer.

Esto último resulta de mucho interés en el campo del estudio de enfermedades neurodegenerativas y en general a las Neurociencias, pues con estos estudios se puede aproximar al cómo o de qué manera evolucionan ciertas áreas del cerebro y la conectividad neuronal, no solo en función de los años sino que también puede sugerir el comportamiento del tránsito normalidad-enfermedad de estas zonas y conexiones.

MÉTODOS

Adquisición de las imágenes

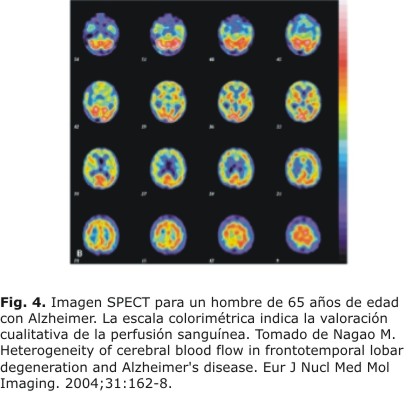
Las imágenes cerebrales tridimensionales, llevadas a cabo por Nagao y otros²¹ fueron obtenidas por SPECT (figura 4).

Esta técnica de neuroimagen consiste en que por medio de la inyección de un radio fármaco marcado con ^99mTecnecio (hexametilen-propilen amino oxima o HMPAO) que tiene aproximadamente 6 h de vida media de duración suministrada de ^99mTc-HMPAO, fue de aproximadamente de 740 MBq. El radio fármaco fue inyectado a través de la vena antecubital mientras el sujeto yacía en una posición codal con los ojos cerrados en una habitación aislada. El SPECT fue ejecutado 5 min después de la inyección del radio fármaco, a través de un escáner (SPECT-2000H; Hitachi Medical Corp. Toyo, Japón) incorporado de una cámara de gammafría de cuatro cabezales detectores. El tamaño del píxel de las imágenes obtenidas fue de 2 mm x 2 mm x 2 mm, es posible visualizar y estudiar la perfusión sanguínea cerebral, a través de un escáner computarizado programado para tal fin, el cual muestra las áreas o zonas cerebrales del CBF reveladas por el radio fármaco que se fija en el tejido cerebral de forma proporcional al flujo sanguíneo (ver figura 1). Las áreas o zonas cerebrales de interés en el estudio fueron la zona posterior y anterior.

Cálculos de las dimensiones fractales

En geometría fractal la dimensión fractal es un parámetro que es útil para caracterizar estructuras complejas.

El procedimiento llevado a cabo por Nagao y otros,²¹ para el cálculo de las dimensiones fractales, fue el siguiente:

Una vez obtenidas las imágenes, procedieron a calcular las dimensiones fractales para las poblaciones estudiadas (21 pacientes con Alzheimer y 11 sujetos normales) mediante la analogía de la relación de escalas en Geometría Fractal entre una medida M y una escala e (ecuación 1):

La ecuación 1 describe cómo la propiedad del objeto (o del sistema) M depende de la escala e a la cual esta propiedad es medida. En el estudio de Nagao y otros,²¹ M(e) representa el número de voxel (pixeles volumétricos) de la imagen tridimensional cerebral del SPECT y e representa las escalas de observación seleccionadas o los niveles de corte (cut-off level) de la radioactividad máxima, las cuales fueron a un 35 % y 50 %.

La dimensión fractal D fue determinada mediante una gráfica de regresión lineal de logaritmos naturales de la ecuación 1 entre el número total de voxel medido -M(e)- y el logaritmo de los niveles de corte (cut-off level)-e- de la pendiente de la recta (ver figura 5).

En este caso la dimensión fractal es un número adimensional que caracteriza la irregularidad o complejidad de la distribución del flujo sanguíneo cerebral (CBF) para las poblaciones arriba mencionadas. Las dimensiones fractales para estos grupos se muestran en las tablas 1 y 2.²¹

 

Tabla 1. Dimensiones fractales (D) para la población de Alzheimer²¹

Paciente Alzheimer	Zona posterior	Zona anterior
	D	D
1	0,70	0,88
2	0,72	0,94
3	0,77	0,97
4	0,82	0,98
5	0,74	1,07
6	0,86	1,11
7	0,84	1,12
8	0,85	1,27
9	0,97	1,33
10	0,93	1,35
11	0,98	1,34
12	0,93	1,44
13	0,92	1,45
14	1,02	1,15
15	1,14	1,28
16	1,06	1,36
17	1,09	1,40
18	1,32	1,39
19	1,02	1,46
20	1,11	1,47
21	1,06	1,36

 

 

Un análisis de varianza por el método de Bonferroni fue usado por Nagao y otros²¹para determinar las comparaciones entre las dos poblaciones y las zonas analizadas. Los resultados mostraron que hubo una significancia estadística entre las dimensiones fractales anterior y posterior de los grupos Alzheimer y normales.

Cálculo de los coeficientes de expansión fractal

Waliszewski y Konarski²⁴ dedujeron un coeficiente de expansión fractal para un objeto o proceso dinámico con dimensión fractal que se expande en un espacio circundante. Los resultados mostraron que los valores de los coeficientes de expansión fractal obtenidos están íntimamente asociados con un incremento o decremento en la conectividad del sistema.

La ecuación que define el coeficiente de expansión para objetos o procesos dinámicos con dimensión fractal que se expanden dentro de su espacio circundante de dimensión euclidiana es:²⁴

(2)

Donde D es la dimensión fractal del objeto o proceso dinámico a estudiar, es decir, en el presente trabajo es una medida de la heterogeneidad (irregularidad) del CBF, W es la dimensión entera o euclidiana del espacio circundante en que se expande o distribuye el CBF, y S es el coeficiente de expansión fractal del CBF, o sea un índice que cuantifica en qué tanto acontece la expansión del CBF respecto a su espacio euclidiano próximo circundante.

De la relación matemática que lo define (2), el coeficiente de expansión fractal posee las siguientes características:

- Si el proceso dinámico u objeto dinámico ocupa enteramente el espacio euclidiano, D = W y S = 0, entonces no hay espacio disponible para la expansión y tal sistema es no interactivo.

- Si el proceso dinámico presenta dimensión fractal y D < W, entonces S < 0, indicando que hay espacio privilegiado para ser ocupado por el objeto o proceso dinámico. Esto se asocia con un incremento en la conectividad del sistema. En general para los procesos que en su crecimiento o evolución espacial exhiben complejidad (irregularidad, fractalidad) sus coeficientes de expansión fractal son menores que cero. Entre más negativo sea el valor de S se dice que el sistema presenta una mayor conectividad para su expansión.

- Si el proceso dinámico presenta dimensión fractal y D > W, entonces S > 0, lo que quiere decir que no hay espacio privilegiado para ser ocupado por el objeto o el proceso dinámico. Esto se asocia con un decremento en la conectividad del sistema. Cuando los procesos presentan características de estados en suspensión y en formación de agregados es posible que los coeficientes de expansión fractal sean mayores que cero.²⁵

Se sabe que el CBF en Alzheimer está asociado con una disfunción neuronal y una pérdida progresiva en la conexión neuronal.^26,27 Partiendo de los datos de la dimensiones fractales halladas por Nagao y otros ²¹ (Tablas 1 y 2) determinaron los coeficientes de expansión fractal del CBF en las poblaciones en cuestión. El coeficiente de expansión fractal, para este estudio, estima la expansión de la distribución heterogénea del CBF respecto al espacio disponible en que puede darse dicha expansión en los grupos de Alzheimer y normal, esto es, cuantifica la evolución espacial de la distribución del CBF, además que sugiere la correlación con la conectividad del sistema donde ocurre la expansión del CBF: las zonas o áreas del cerebro posterior y anterior que se encuentran mediadas por la interconexión neuronal.

RESULTADOS

Los resultados de los coeficientes de expansión obtenidos para la población de Alzheimer y normales se muestran en las tablas 3 y 4, respectivamente.

Tabla 3. Coeficientes de expansión fractal (CEF) para Alzheimer

Paciente Alzheimer	Zona posterior		Zona anterior
	W	CEF	W	CEF
1	1	-0,300	1	-0,120
2	1	-0,280	1	-0,060
3	1	-0,230	1	-0,030
4	1	-0,180	1	-0,020
5	1	-0,260	2	-0,465
6	1	-0,140	2	-0,445
7	1	-0,160	2	-0,440
8	1	-0,150	2	-0,365
9	1	-0,030	2	-0,335
10	1	-0,070	2	-0,325
11	1	-0,020	2	-0,330
12	1	-0,070	2	-0,280
13	1	-0,080	2	-0,275
14	2	-0,490	2	-0,425
15	2	-0,430	2	-0,360
16	2	-0,470	2	-0,320
17	2	-0,455	2	-0,300
18	2	-0,340	2	-0,305
19	2	-0,490	2	-0,270
20	2	-0,445	2	-0,265
21	2	-0,470	2	-0,320

W: espacio circundante en que sucede la expansión.

Para una valoración objetiva de los resultados entre los valores de los CEF en los grupos Alzheimer y normal, se comparan respecto al espacio euclidiano W en que sucede la expansión.

En la Zona posterior:

Los valores de los coeficientes de expansión fractal del lado posterior del cerebro para los grupos de Alzheimer y normal respecto a la expansión del CBF que sucede en el espacio circundante euclidiano W (o de dimensión topológica entera) de 1, se encuentran en el rango entre -0,300 a -0,020 con media (desviación estándar) de -0,152 (0,094), y en el rango entre -0,370 a -0,050 con media de -0,271 (0,098), para las poblaciones Alzheimer y normal, respectivamente. En este caso del lado posterior, los valores de los coeficientes referenciados a la expansión que sucede en el espacio W de 2 para el grupo Alzheimer, variaron en el rango entre -0,490 a -0,340 con media de -0,449 (0,048). En el grupo de normales no se registran valores de coeficientes respecto a W 2 en esta zona, puesto que las dimensiones fractales en todos los individuos analizados para esta población no son mayores a 1 (tablas 3 y 4).

En la Zona anterior:

Los valores de los coeficientes de expansión fractal del lado posterior del cerebro para los grupos de Alzheimer y normal respecto a la expansión del CBF que sucede en el espacio circundante euclidiano W de 1, se encuentran en el rango entre -0,120 a -0,020 con media (desviación estándar) de -0,058 (0,045), y en el rango entre -0,200 a -0,030 con media de -0,107(0,065), para los grupos Alzheimer y normal, respectivamente. En esta zona los coeficientes en relación con la expansión en el espacio W de 2 para las poblaciones de Alzheimer y normal, variaron en el rango entre -0,465 a -0,265 con media de -0,343 (0,065), y -0,485 a -0,415 con media de -0,448 (0,028), respectivamente (tablas 3 y 4).

Además, se observa que todos los coeficientes obtenidos para las dos zonas evaluadas son menores a cero, esto es de esperarse debido a la inherente fractalidad del fenómeno en cuestión, esto es, la propiedad de que en el sistema estudiado, en nuestro caso la distribución del CBF, su comportamiento exhiba irregularidad, es decir, dimensión fractal o fraccionaria y no entera.

DISCUSIÓN

Este es el primer trabajo en caracterizar la expansión fractal espacial de la distribución del CBF en personas con Alzheimer y sanos. Los coeficientes de expansión fractal para la región posterior en la población de Alzheimer mostraron ser mayores que en los sujetos normales, comparadas proporcionalmente en el espacio circundante disponible para la expansión W. Esto es una medida matemática de la manera en que se expande y se distribuye el CBF, sugiriendo la irregularidad o heterogeneidad que el CBF presenta en dicha zona, además del grado de conectividad en esa región. En la enfermedad Alzheimer el grado de heterogeneidad del CBF en el lado posterior respecto a los normales está asociada por el grado de conectividad del espacio en que sucede la expansión y, este grado de conectividad en Alzheimer es menor en dicha zona (valores de CEF cercanos a cero), por la relación en que existe un deterioro en la interconexión (o conectividad) neuronal de esta área del cerebro en personas que padecen la enfermedad, tal como se ha evidenciado en distintas investigaciones.^26,27 De igual forma es posible afirmar que los coeficientes de expansión fractal comparados en el espacio para la expansión W en sanos son menores (valores de CEF alejados de cero en valores negativos) respecto a los pacientes de Alzheimer, dado que en aquellos sujetos normales la conectividad neuronal es más elevada y por lo tanto eficiente la manera en que sucede la distribución del CBF en la zona.

Para la región anterior los resultados muestran que, al igual que la zona posterior, los coeficientes de expansión fractal son mayores en Alzheimer, comparados respecto al espacio W, en relación con el normal, por lo que evidencia un grado de conectividad menor de la región anterior para el grupo de Alzheimer (valores de CEF cercanos a cero), grado asociado de igual forma al debilitamiento de esta zona del cerebro con la interconectividad neuronal.

Estos resultados se corroboran con las investigaciones,^23,28-30 los cuales evidencian un deterioro progresivo y global que sufre dicha zona cerebral, posterior y anterior, en personas que padecen Alzheimer. De igual manera este resultado se relaciona con otras investigaciones que hacen uso de la geometría fractal en aplicaciones biomédicas,^31-35 en cuyos hallazgos se evidencia la diferenciación matemática entre enfermos y sanos, se enfatiza en la objetividad y reproducibilidad que nos ofrecen los conceptos de la teoría fractal.

El CBF está asociado con la disfunción neuronal.^26,27 La comprensión del CBF en personas con Alzheimer es de interés porque permite aproximarse a la fisiología cerebral de la enfermedad y, en esa medida, entender la actividad neuronal del cerebro cuando se padecen estos tipos de enfermedades neurodegenerativas. De esta manera un método que cuantifica la expansión de la distribución del CBF en personas con Alzheimer y en sujetos normales resulta relevante, puesto que se está valorando, cuantitativamente, el daño que sufren ciertas zonas del cerebro con el transcurso de los años Alzheimer, particularmente en las zonas posterior y anterior. El coeficiente de expansión fractal permite cuantificar la expansión de la fractalidad del flujo sanguíneo cerebral en pacientes con Alzheimer, al mismo tiempo que sugiere el grado de conectividad neuronal de estas zonas.

En el presente trabajo se cuantificó la expansión de la distribución del CBF en sujetos con Alzheimer y en sujetos que no la padecen, se pudo encontrar que la estructura fractal espacial de la expansión de la distribución del CBF para los pacientes de Alzheimer se diferencia matemáticamente de aquellos que no la padecen, comparadas respecto al espacio disponible en que sucede dicha expansión. Esto último tiene implicaciones en el tránsito salud-enfermedad, pues corrobora las investigaciones que dan cuenta de que el envejecimiento humano prefiere la irregularidad o el caos antes que la regularidad u orden.^36-38

El coeficiente de expansión fractal está asociado con la conectividad del sistema y caracteriza la expansión del objeto fractal en el espacio. Por tanto este coeficiente sugiere de qué manera la distribución del flujo sanguíneo cerebral CBF (fractal) se expande en ciertas zonas del cerebro en personas que presentan Alzheimer y en aquellas que no la padecen. De tal manera que al determinar dicho coeficiente, estamos valorando el grado de conectividad neuronal (asociado con la distribución del CBF) entre enfermos de Alzheimer y en sujetos normales.

Esta relación matemática del CBF muestra ser una metodología objetiva que permitiría extenderse en aplicaciones clínicas, de diagnóstico y tratamiento en enfermedades neurodegenerativas para valorar la fisiología cerebral del Alzheimer y otros desórdenes neurológicos, pues la valoración de un diagnóstico a través de las imágenes de SPECT en Alzheimer está mediada por el nivel de experticia del observador.³⁹ Además permite cuantificar el daño progresivo de ciertas zonas del cerebro en la enfermedad Alzheimer.

Los resultados obtenidos tienen implicaciones para el estudio teórico de la neurodinámica sanguínea del Alzheimer, como también en el desarrollo y efectos de neurofármacos.

Agradecimientos

Al Dr. Michinobu Nagao, Director del Departament of Molecular Imaging and Diagnosis, GraduateSchool of Medical Science, Kyushu University, Fukuoka, Japón por haber facilitado y autorizado el uso de los datos de las dimensiones fractales obtenidas en su investigación publicada.²²

REFERENCIAS BIBLIOGRÁFICAS

1. Cassimjee N. Neurobiology of Alzheimer's Disease. Neuropsychological symptoms and premorbid temperament traits in Alzheimer's dementia [tesis de PhD]. Dept. Psych. Universidad de Pretoria, Sudafrica; 2003

2. Alzheimer's Disease International. World Alzheimer Report; 2009.

3. Elnashaie S, Mahecha-Botero A. Towards understanding Alzheimer's and Parkinson's. Pharmaceuticals. 2005;2:29-31.

4. Guruprased BR, Kumar S. Computational Biology of Alzheimer's disease: Disease with Bioinformatics. VDM Verlag; 2010.

5. Gomez Ravetti M. Uncovering Molecular Biomarkers That Correlate Cognitive Decline with the Changes of Hippocampus' Gene Expression Profiles in Alzheimer's Disease. PLoS ONE. 2010;5(4).

6. Rishnamurthy V. Computational Identification of Alzheimer's Disease Specific Transcription Factors using Microarray Gene Expression Data. J Proteomics Bioinform. 2009;2:505-8.

7. Allam AR. Bioinformatic Analysis of Alzheimer's Disease and Type2 Diabetes Mellitus: A Bioinformatic Approach. J Proteomics Bioinform; 2008.

8. Stanley E . Statistical Physics and Alzheimer's Disease. Physica A. 1998;249:460-71.

9. Reis AES. A Computational Mathematical Model of Neuronal Death Caused by Oxidative Stress in Alzheimer's Disease. Proceeding of II International Symposium on Mathematical and Computational Biology. Río de Janeiro, Brasil; 2005.

10. Macdonals A, Pritchard D, A Mathematical model of Alzheimer's disease and the APOE Gene. Astin Bulletin. 2000;30(I):69-110.

11. Sharma V. Deterministic Chaos and Fractal Complexity in the Dynamics of cardiovascular behavior. The Open Cardiovascular Medicine Journal. 2009;3:110-23.

12. Fernandez E. Use of Fractal Theory in Neuroscience: Methods, Advantages, and Potential. Problems. Methods. 2009;24:309-21.

13. Weibel ER. Fractal geometry: a design principle for living organisms. Am J Physiol. 1991:261:L361-L369.

14. Bassingthwaighte JB, Liebovitch LS, West JB. Fractal Physiology. Oxford: Oxford University Press;1994. p. 29-31.

15. Havlin S. Fractals in Biology and Medicine. Chaos, Solitons & Fractals. 1995;6:171-201.

16. Rudolf Karch. Fractal properties of Perfusion Heterogeneity in Optimized Arterial Trees: A model Study. The Journal of General Physiology. 2003;122:307-21.

17. Sonntag M. Spatial heterogeneity of blood flow in the dog heart. I. Glucose uptake, free adenosine and oxidative/glycolytic enzyme activity. Pflugers Arch. 1996;432:439-50.

18. Glenny RW, Robertson HT. Fractal modeling of pulmonary blood flow heterogeneity. J Appl Physiol. 1991;70:1024-30.

19. Nagao M Murase K. Measurement of heterogeneous distribution on Technegas SPECT images by three-dimensional fractal analysis. Ann Nucl Med. 2002;16:369-76.

20. Iversen PO, Nicolaysen G. Fractals describe blood flow heterogeneity within skeletal muscle and within myocardium. Am J Physiol. 1995;268:H112H116.

21. Nagao M. Heterogeneity of Cerebral Blood Flow in frontotemporal lobar degeneration and Alzheimer's disease. Eur J Nucl Med Mol Imaging. 2004;31:162-8.

22. Nagao M. Fractal analysis of Cerebral Blood Flow distribution in Alzheimer's disease. J Nucl Med. 2001;42:1446-50.

23. Nagao M. Heterogeneity of posterior limbic perfusion in very early Alzheimer's disease. Neuroscience Research. 2006;55:285-91.

24. Waliszewski P, Konarski J. Fractal Strucutre of Space and Time is Necessary for the Emergence of Self-Organization, Connectiviy, and Collectivity in Cellular System. Fractals in Biology and Medicine. 2002;vol. III.

25. Waliszewski P. Self-similarity, Collectivity, and evolution of fractal dynamics during retinoid-induced differentiation of cancer cell population. Fractals. 1999;7(2):139-49.

26. Davies P Maloney AJF. Selective loss of central cholinergic neurons in Alzheimer's disease. Lancet. 1976;2:1403.

27. Whitehouse PJ. Alzheimer's disease: evidence of selective loss of cholinergic neurons in the nucleus basalis. Ann Neurol.1981;10:122-6.

28. Savva G, Wharton S. Age, Neuropathology, and Dementia. The New England Journal of Medicine. 2009;360(22).

29. Tomlinson BE, Corsellis JA. Ageing and the dementias. In: Adams JH, Corsellis JA, Duchen LW (editores). Greenfield's Neuropathology. 4ta. ed. New York: John Wiley and Sons;1984. p. 951-1025.

30. Insausti R, Insausti AM, Sanz E, Moreno M. Bases morfológicas de la atrofia cortical cerebral en la senescencia y en la enfermedad de Alzheimer. ANALES Sis San Navarra. 1997;20(3):33-8.

31. Rodríguez J. Theoretical generalization of normal and sick coronary arteries with fractal dimensions and the arterial intrinsic mathematical harmony. BMC Medical Physics. 2010;10(1).

32. Rodriguez J. Comportamiento fractal del repertorio T específico contra el alérgeno Poa P9. Rev Fac Med Univ Nac Colombia.2005;53(2):72-8.

33. Rodriguez J. Descripción matemática con dimensiones fractales de células normales y con anormalidades citológica de cuello uterino. Rev Cienc Salud. 2006;4(2):58-63.

34. Rodriguez J. Medidas fractales de radiografías de tórax de pacientes con diferentes patologías. Rev Cienc Salud. 2006;4(1):31-8.

35. Rodriguez J. Comportamiento fractal del ventrículo izquierdo durante la dinámica cardiaca. Revista Colombiana de Cardiología. 2006;13(3).

36. Kyriazis Marios. Practical applications of chaos theory to the modulation of human ageing: nature prefers chaos to regularity. Biogerontology. 2003;4:75-90.

37. Goldberger AL. Fractal dynamics in physiology: Alterations with disease and aging. Proc Natl Acad Sci USA. 2002;99(1).

38. Goldberger AL, Peng CK, Lipsitz A. What is physiologic complexity and how does it change with aging and disease? Neurobiol Aging. 2002;23(1):23-6.

39. Holman BL, Devous MD. Functional brain SPECT: the emergence of a powerful clinical method? J Nucl Med. 1992;33:1888-904.

Recibido: 1ro. de marzo de 2011.
Aprobado: 17 de marzo de 2011.

Andy Domínguez Monterroza. Universidad Nacional de Colombia, Bogotá. Correo electrónico: [e-mail]

Autor para la correspondencia: Diego A. Garzón-Alvarado. Correo electrónico: [e-mail]