ARTÍCULO ORIGINAL

 

Una formulación preliminar de tipo electromecánica para la formación de hueso en un proceso de remodelación

 

Preliminary electromechanical formulation for bone formation in a remodeling process

.

 

Dra. Angélica María Ramírez Martínez^I, Ing. Diego Alexander Garzón-Alvarado^II

^IUniversidad Central de Colombia, Bogotá, Colombia.
^IIUniversidad Nacional de Colombia, Bogotá, Colombia.

 

 

---

RESUMEN

En este artículo se propone un modelo de remodelación ósea que tiene en cuenta los estímulos mecánicos y eléctricos. Bajo estos supuestos, se obtiene la distribución de masa que depende de las cargas mecánicas y eléctricas. El trabajo coloca de manifiesto la importancia del campo eléctrico en el proceso de remodelación y, propone la cuantificación de sus efectos para obtener un modelo aplicable a nivel clínico.

Palabras clave: parámetros de remodelación, huesos, cambio temporal, electromagnetismo.

---

ABSTRACT

A bone remodeling model is proposed which takes account of mechanical and electrical stimuli. Under these assumptions, a mass distribution is obtained which depends on mechanical and electrical loads. The paper reveals the importance of the electric field in the remodeling process, and proposes to quantify its effects with a view to obtaining a clinically applicable model.

Key words: remodeling parameters, bones, temporary change, electromagnetism.

---

 

 

INTRODUCCIÓN

La estructura ósea está compuesta por huesos que le confieren estabilidad mecánica al cuerpo humano y son una fuente de minerales para el metabolismo.¹ Los huesos han sido ampliamente estudiados desde el punto de vista mecánico, mineral y por su funcionalidad.^1,2 Desde el punto de vista mecánico se pueden adaptar a las cargas sobre las trayectorias de esfuerzo mediante la aposición mineral que se hace gracias a la acción de los osteoblastos.^1-4 También, se puede reabsorber el mineral cuando el estímulo mecánico es suficientemente bajo como para encontrar innecesario el mantenimiento de esta estructura.² La reabsorción está dirigida por los osteoclastos. En este sentido, los osteoblastos y osteoclastos son células primordiales en la remodelación ósea que son estimulados por la acción de un medidor de esfuerzos mecánicos como son los osteocitos.² Cada una de estas tres células juega un papel importante en el proceso de recambio, mantenimiento y modelado de los huesos.¹

En el siglo XIX, gracias a los trabajos de Meyer, Wolff⁵ propone una teoría acerca de la arquitectura trabecular del hueso. En esta teoría se supone que sobre las trayectorias de alto esfuerzo mecánico se forma, con mayor densidad, el hueso trabecular. Ya en el siglo XX, en 1987, Frost^6-8 propone un mecanismo de adaptación de la masa ósea en función de las cargas mecánicas. En consecuencia, a partir de la teoría de adaptación del hueso ante las cargas, se han desarrollado un buen número de algoritmos de remodelación ósea, entre los que se destacan los propuestos por Frost,⁸ Pauwels,⁹ Kummer,¹⁰ Cowin^11-13 y Hegedus¹⁴ que predicen la formación de la estructura del hueso a partir de las cargas mecánicas internas que son estudiadas en términos de esfuerzos y deformaciones.

A partir de los modelos mecánicos de remodelación ósea se han hecho sofisticados trabajos sobre el proceso que ocupa la aposición y reabsorción durante el recambio de masa ósea; en especial, se ha estudiado la distribución de masa en el fémur,^15,16 alrededor de prótesis de cadera,^17,18 alrededor de implantes dentales,¹⁹ entre otros. Estos trabajos eran, en general, fenomenológicos, por tanto, varios investigadores hicieron esfuerzos importantes en incluir en los modelos matemáticos, el papel de la biología celular y la bioquímica en el proceso de remodelación. De esta forma, se inicio el estudio, a nivel microscópico, del efecto de las unidades celulares básicas de remodelado (BMU, del inglés Basic Multicellular Units) en el proceso de recambio de tejido.^20,21 Desde la perspectiva de las BMUs, se iniciaron trabajos importantes a niveles bioquímico y mecánico, del efecto de las grietas,²² los ciclos celulares durante la vida adulta,²³ las moléculas activadoras de cada célula²⁴ y la distribución espacial de cada BMU.²⁵ Con estos importantes avances en el conocimiento de la remodelación ósea, los investigadores en el tema, incursionaron, cada vez más, en el estudio de otros estímulos biofísicos que pueden afectar este proceso. En general, la mayoría de modelos no tenían en cuenta (o era implícito en el modelo) los fenómenos físico-químicos de mecanotransducción del tejido. Por esta razón se hicieron nuevas investigaciones que abrieron paso al estudio del comportamiento piezoeléctrico y electrocinético del hueso.²⁶

Alternamente, de forma clínica, se había encontrado que el campo electromagnético aplicado a los huesos acelera el proceso de cicatrización luego de la fractura ósea.²⁶ Es así como el artículo publicado por Demiray y Dost,²⁷ inicia una nueva línea de investigación sobre el efecto que el campo electromagnético tiene sobre el daño interno del hueso. En otro artículo, Ramtani²⁶ realiza un modelo matemático sobre el beneficio que tiene el campo eléctrico en la reparación del daño y el mantenimiento de la matriz sólida del hueso. Adicionalmente se ha estudiado el comportamiento eléctrico del tejido óseo en la producción de campo eléctrico y ante flujo eléctrico externo. Fukada y Yasuda²⁸ demostraron que el hueso se comporta como un piezoeléctrico, es decir, los esfuerzos mecánicos crean polarización eléctrica (el efecto indirecto) y el campo eléctrico externo causa deformación (el efecto conversor). Además, se han determinado las propiedades de los huesos para producir potenciales piezoeléctricos.^29-33 Este conjunto de datos ha propiciado el desarrollo de modelos matemáticos que incluyen el efecto de los campos electromagnéticos en el proceso de reparación^34,35 y de remodelación ósea.³⁶ Por ejemplo, Qu y Yu³⁴ desarrollan un modelo matemático (sin dimensión espacial) del proceso de remodelación y cicatrización bajo el efecto de cargas mecánicas y el uso de cargas eléctricas. En este modelo, se logra apreciar que a mayor voltaje aplicado a un hueso, después de la fractura, disminuye el porcentaje de hueso con daño y microdaño en pocos días después del estímulo. De igual forma, durante el transcurrir de la osteoporosis se ha modelado el efecto del campo eléctrico, por lo que, la densidad del hueso aumenta en el tiempo. De otro lado, Huang y otros³⁷ establecen la hipótesis sobre las vías bioquímica y biológica, mediante la cual se activan las células, en especial los osteocitos, durante la imposición de campo eléctrico. De igual forma, Qu y Yu³⁸ proponen un modelo matemático que permite incluir las cargas mecánicas y el efecto electromagnético en el proceso de remodelación ósea.

Hasta la fecha no se han realizado modelos de remodelación ósea, de carácter fenomenológico, que sean probados y comparados con modelos puramente mecánicos. Por tanto, en este artículo se propone un nuevo modelo electromecánico de remodelación del tejido óseo. Para probar su funcionamiento se hacen diferentes pruebas numéricas y se comparan con modelos típicos previos, desde el enfoque mecánico, hechos por otros autores. Las constantes del modelo eléctrico son halladas a partir de la literatura correspondiente y por experimentación numérica. A partir de estas hipótesis se puede concluir que el campo eléctrico puede afectar la distribución de masa que se origina mediante el proceso de remodelación bajo el efecto mecánico, únicamente. De hecho, el campo eléctrico puede aumentar la densidad del tejido óseo y acelerar el proceso de aposición. Para este objetivo se utilizó, como punto de partida, el modelo de remodelación de Nackenhorst,³⁹ al cual se le adicionó el efecto del campo eléctrico. De esta forma, el modelo propuesto puede ser un punto de partida para nuevos trabajos sobre los efectos eléctricos en el mantenimiento de los huesos. Se propone además, hallar las constantes más próximas a la realidad, para que el modelo pueda ser usado a nivel clínico.

 

EL MODELO ELECTROMECÁNICO

El modelo electromecánico de remodelación ósea en el que intervienen los estímulos mecánicos y eléctricos puede ser escrito, hipotéticamente, de la siguiente forma (1):

 

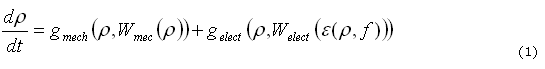
donde es el estímulo mecánico, que depende de la densidad del tejido (r (x, y, z, t)), y del trabajo realizado por los esfuerzos mecánicos y es el estímulo eléctrico que depende de la densidad, la frecuencia y el trabajo realizado por el campo eléctrico . En esta primera aproximación se considera que los dos estímulos se adicionan para determinar el proceso de remodelación ósea. A continuación se desarrollará cada uno de los términos que determinan el modelo electromecánico.

A. El modelo mecánico

Siguiendo el modelo mecánico de remodelación descrito en Weinans⁴ y Nackenhorst,³⁹ la variación de la densidad en el tiempo depende del estímulo mecánico que existe en cada punto espacial del hueso, lo cual puede ser escrito como (2):³⁹

 

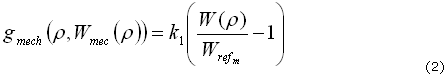
Donde r es la densidad del tejido óseo en cada punto del espacio (r (x, y, z, t)), W(r) es la energía de deformación por unidad de volumen que se debe a las cargas mecánicas, k₁ es una constante y W_REFm es la energía de deformación (por unidad de volumen) de referencia que establece el umbral para el cual se llevará a cabo un proceso de aposición (W(r)/W_REFm >1) o reabsorción (W(r)/W_REFm < 1) del tejido,³⁹ en presencia de cargas mecánicas. Se debe notar que la energía de deformación depende de la densidad, y está dada por (3):

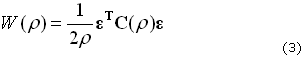
donde e es la deformación, en notación Voigt, del tensor de deformación dado (4):

que es función de los desplazamientos, dados por (5):

 

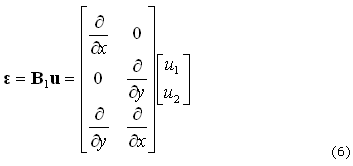
Por su parte, C(r) es la matriz de elasticidad lineal. La matriz C(r) contiene el módulo de Poisson, que en general se considera constante, y el módulo de Young que depende de la densidad mediante la expresión (7): ⁴

 

Donde A es una constante y n establece una relación de potencia de la densidad, que se ha hallado mediante evidencias experimentales.³⁹

Al manipular la ecuación (7) se puede obtener una forma adimensional de la densidad, más sencilla de trabajar, con el objetivo de determinar el módulo de elasticidad. Multiplicando el lado derecho de (7) por se tiene (8):

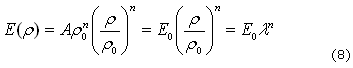
Donde y son el módulo de elasticidad y la relación de densidades adimensional, respectivamente. Por tanto la matriz de elasticidad lineal se puede expresar como (9):

Donde C₀ es la matriz de elasticidad lineal con coeficientes constantes, que depende de E₀ y n, únicamente, y que está dada, en el caso de esfuerzo plano, por: (10)

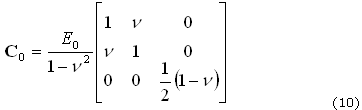
De esta forma, la energía de deformación por unidad de volumen (3) se puede expresar como (11):

Dondees la energía de deformación en cada instante del tiempo, que se calcula, únicamente, con las constantes iniciales del problema de remodelación.³⁹ Reemplazando estas ecuaciones en (2) y con alguna manipulación algebraica se tiene 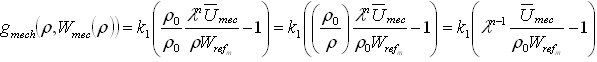(12):

(12)

donde se puede definir , por tanto se tiene la siguiente ecuación para la relación de densidades (13):

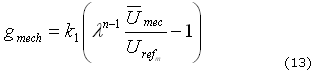
De otro lado, la ecuación de momentum que establece los esfuerzos internos de un cuerpo está dada por (14):⁴⁰

donde el esfuerzo está dado por (15):

B. Modelo eléctrico

En este artículo se propone la inclusión de un término eléctrico, hipotético, que puede determinar, parcialmente, el proceso de remodelación ósea. De esta forma, la contribución de este estimulo se puede escribir como (16):

donde e(r, ƒ) es la permitividad eléctrica del tejido óseo, que depende de la densidad (r) y la frecuencia (ƒ); es la energía eléctrica por unidad de volumen, k₂ es una constante y W_REFe es la energía eléctrica (por unidad de volumen) de referencia.

Se debe notar que el término energía eléctrica depende de la permitividad, que a su vez depende de la densidad y la frecuencia. Este término energético está dado por (17):

donde es la intensidad eléctrica (campo eléctrico), e(r, ƒ) es la permitividad eléctrica, que depende de la densidad y la frecuencia, y está dada por (18):

Donde es la permitividad en el espacio vacío y es la permitividad relativa, que a su vez está dada por (19):

Donde B es una constante y m establece una relación de potencia de la densidad, que se puede hallar mediante experimentación, y que será desarrollada en secciones posteriores. De otro lado, se tiene que d (ƒ) es función de la frecuencia a la cual se aplica el campo eléctrico.

De igual forma que para el caso mecánico, se puede manipular la ecuación (19) para que quede expresada en términos de la densidad relativa, multiplicando el primer sumando por , por lo que se obtiene (20):

donde es una constante para el modelo de potencia de la permitividad relativa. Por tanto, reemplazando (20) en (17), se obtiene 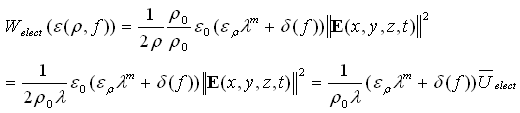(21):

(21)

 

donde

Reemplazando la anterior ecuación (21) en (16) se tiene (22):

(22)

Donde se ha elegido como el valor de referencia de la energía eléctrica.

De otro lado, la ley de Gauss para campo eléctrico, sin cargas internas, está dada por (23):

Donde y es la densidad de carga eléctrica. A su vez, el campo eléctrico se puede expresar en términos de una cantidad denominada potencial eléctrico o voltaje, dada por (24):

donde f es el potencial eléctrico.

En resumen, la ecuación (1) se puede escribir como (25):

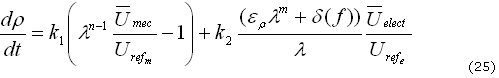
Nuevamente, utilizando adimensionalización, del lado izquierdo de la ecuación, se obtiene (26):

Donde y son las constantes mecánica y eléctrica que definen la tasa de transformación de remodelación ósea, dependiente de cargas mecánicas y del potencial eléctrico, respectivamente.

 

DISCUSIÓN

En este artículo se propone un modelo de remodelación ósea que incluye carga mecánica con el supuesto de la imposición de campo eléctrico en el dominio. Para calcular el estímulo mecánico y eléctrico de remodelación, y la evolución de la densidad se utiliza el enfoque de energía de deformación y energía eléctrica. Este artículo es pionero en incluir el efecto eléctrico en un modelo de remodelación ósea, previamente concebido por Weinans y otros.⁴ Además se plantea la necesidad de incluir las constantes eléctricas y mecánicas que deben ser halladas mediante experimentación. Con estas constantes se logrará obtener todos los ingredientes necesarios para resolver el problema de forma numérica y comparar los resultados con aquellos que tienen en cuenta únicamente la mecánica en el remodelado óseo.

Una limitación inherente al modelo es la linealidad del efecto de las cargas mecánicas y los campos eléctricos sobre el proceso de aposición y reabsorción de masa ósea. Aún, hoy en día, los modelos de remodelación ósea, en su gran mayoría siguen siendo modelos lineales, que no tienen en cuenta el proceso de saturación de cada proceso. Este será una limitación a resolver en futuros trabajos en el tema.

En conclusión, el modelo aquí descrito se constituye en una primera aproximación matemática al proceso de remodelado electromecánico que tiene en cuenta el efecto de la energía sobre el comportamiento de absorción y deposición.

 

 

REFERENCIAS BIBLIOGRÁFICAS

1. Ganong WF, William F. Fisiologia Médica. México DF: El Manual Moderno; 2006. p. 373-86.

2. Cowin SC. Bone mechanics handbook. USA: CRC press; 2001.

3. Jacobs CR, Simo JC, Beaupre GS, Carter DR. Adaptive bone remodeling incorporating simultaneous density and anisotropy considerations. Journal of biomechanics. 1997;30:603-13.

4. Weinans H, Huiskes R, Grootenboer H. The behavior of adaptive bone-remodeling simulation models. Journal of biomechanics. 1992;25:1425-41.

5. Wolff J. Das gesetz der transformation der knochen. Berlin: Hirschwald; 1892. p. 1-139.

6. Frost HM. The laws of bone structure. Springfield, IL: Charles C Thomas; 1964.

7. Frost HM. Mathematical elements of lamellar bone remodeling. Springfield, IL: Charles C Thomas; 1964.

8. Frost HM. Vital biomechanics: proposed general concepts for skeletal adaptations to mechanical usage. Calcified Tissue International. 1988;42:145-56.

9. Pauwels F. Gesammelte abhandlungen zur funktionellen anatomie des bewegungsapparates. Berlín: Springer-Verlag; 1965. 183-96.

10. Kummer B. Biomechanics of bone: Mechanical properties, functional structure, functional adaptation. En: Fung YC, Perrone N, AnlicKer M (eds.) Biomechanics: Its foundation and objectives. Englewood Cliffs (N.J.): Prentice-Hall, 1972. p. 237-71.

11. Cowin S. Wolffís law of trabecular architecture at remodeling equilibrium. Journal of biomechanical engineering. 1986;108:83.

12. Cowin S, Hegedus D. Bone remodeling I: theory of adaptive elasticity. Journal of Elasticity. 1976;6:313-26.

13. Cowin S, Nachlinger RR. Bone remodeling III: uniqueness and stability in adaptive elasticity theory. Journal of Elasticity. 1978;8:285-95.

14. Hegedus D, Cowin S. Bone remodeling II: small strain adaptive elasticity. Journal of Elasticity. 1976;6:337-52.

15. Gupta S. New AMR, Taylor M. Bone remodelling inside a cemented resurfaced femoral head. Clinical Biomechanics. 2006;21:594-602.

16. Stülpner, M., Reddy, B., Starke, G. & Spirakis, A. A three-dimensional finite analysis of adaptive remodelling in the proximal femur. Journal of biomechanics. 1997;30;1063-66.

17. Jonkers I, Sauwen N, Lenaerts G, Mulier M, Van de Perre G, Jaecques S. Relation between subject-specific hip joint loading, stress distribution in the proximal femur and bone mineral density changes after total hip replacement. Journal of biomechanics. 2008;41:3405-13.

18. García J, Doblaré M, Cegoñino J. Bone remodelling simulation: a tool for implant design. Computational materials science. 2002;25:100-114.

19. Lian Z, Guan H, Ivanovski S, Loo YC, Johnson NW, Zhang H. Effect of bone to implant contact percentage on bone remodelling surrounding a dental implant. International journal of oral and maxillofacial surgery. 2010;39:690-98.

20. Martin R. Targeted bone remodeling involves BMU steering as well as activation. Bone. 2007;40:1574-80.

21. Hernández C, Hazelwood S, Martin R. The relationship between basic multicellular unit activation and origination in cancellous bone. Bone. 1999;25:585-87.

22. Taylor D, Tilmans A. Stress intensity variations in bone microcracks during the repair process. Journal of theoretical biology. 2004;229:169-77.

23. Hernandez C, Beaupre,G, Carter D. A theoretical analysis of the changes in basic multicellular unit activity at menopause. Bone. 2003;32:357-63.

24. Peterson MC, Riggs MM. A physiologically based mathematical model of integrated calcium homeostasis and bone remodeling. Bone. 2010;46:49-63.

25. Buenzli PR, Pivonka P, Smith DW. Spatio-temporal structure of cell distribution in cortical bone multicellular units: a mathematical model. Bone. 2011; 48(4):918-26.

26. Ramtani S. Electro-mechanics of bone remodelling. International Journal of Engineering Science. 2008;46:1173-82.

27. Demiray H, Dost S. The effect of quadrupole on bone remodeling. International Journal of Engineering Science. 1996;34:257-68.

28. Fukada E. Yasuda I. On the piezoelectric effect of bone. J Phys Soc Japan. 1957;12:1158-62.

29. Aschero G, Gizdulich P, Mango F, Romano S. Converse piezoelectric effect detected in fresh cow femur bone. Journal of biomechanics. 1996;29:1169-74.

30. Beck BR, Qin Y, Rubin C, McLeod K, Otter M. The relationship of streaming potential magnitude to strain and periosteal modeling. Medicine & Science in Sports & Exercise. 1997;29(5):S98.

31. Gross D, Williams WS. Streaming potential and the electromechanical response of physiologically-moist bone. Journal of biomechanics. 1982;15:277-95.

32. Hung C, Allen F, Pollack S, Brighton C. What is the role of the convective current density in the real-time calcium response of cultured bone cells to fluid flow? Journal of biomechanics. 1996;29:1403-09.

33. Johnson MW, Chakkalakal DA, Harper RA, Katz JL. Comparison of the electromechanical effects in wet and dry bone. Journal of biomechanics. 1980;13;437-42.

34. Qu CY, Yu SW. The damage and healing of bone in the disuse state under mechanical and electro-magnetic loadings. Procedia Engineering. 2011;10:171-76.

35. Wang E, Zhao M. Regulation of tissue repair and regeneration by electric fields. Chinese Journal of Traumatology (English Edition). 2010;13:55-61.

36. Demiray H. Electro-mechanical remodelling of bones. International Journal of Engineering Science. 1983;21:1117-26.

37. Huang CP, Chen XM, Chen ZQ. Osteocyte: the impresario in the electrical stimulation for bone fracture healing. Medical hypotheses. 2008;70:287-90.

38. Qu C, Qin QH, Kang Y. A hypothetical mechanism of bone remodeling and modeling under electromagnetic loads. Biomaterials. 2006;27:4050-57 ().

39. Nackenhorst U. Numerical simulation of stress stimulated bone remodeling. Technische Mechanik. 1997;17:31-40.

40. Oñate E. Structural analysis with the finite element method. Linear statics. Barcelona: Springer Verlag; 2009. p. 5-250,

 

 

Recibido: 3 de septiembre de 2011.
Aprobado: 26 de septiembre de 2011.

 

 

Angélica María Ramírez Martínez. Grupo de Bioingeniería. Universidad Central de Colombia, Bogotá, Colombia. Correo electrónico: [e-mail]