ARTÍCULO ORIGINAL

 

Modelado computacional del desarrollo óseo humano en la placa de crecimiento del fémur distal

 

Computational modeling of human bone development in the distal femoral growth plate

 

MSc. Carlos Alberto Narváez-Tovar^I,II, Ing. Diego Alexander Garzón-Alvarado^II

^IFacultad de Ingeniería Mecánica. Universidad Santo Tomás. Bogotá, Colombia.
^IIDepartamento de Ingeniería Mecánica y Mecatrónica. Universidad Nacional de Colombia. Bogotá, Colombia.

 

 

---

RESUMEN

La elongación de los huesos largos se produce principalmente por la proliferación e hipertrofia de los condrocitos presentes en las placas de crecimiento. Bajo la hipótesis que el comportamiento de estas células depende de factores bioquímicos y mecánicos, este artículo presenta un modelo computacional por elementos finitos que simula el comportamiento de la placa de crecimiento del fémur distal humano. Se emplea un dominio bidimensional en el que se identifican las regiones de hueso trabecular metafisial y episifial que encierran a la placa de crecimiento y las regiones de cartílago inerte y columnar. La validación del modelo se realiza a partir de la histología correspondiente a la placa de crecimiento del fémur distal de un niño de dos años. Los resultados obtenidos demuestran que el modelo simula el crecimiento y el comportamiento de la placa metafisiaria regulada por su actividad celular y las cargas mecánicas.

Palabras clave: placa de crecimiento, elementos finitos, fémur, hipertrofia, condrocitos.

---

ABSTRACT

Long bone elongation is mainly due to proliferation and hypertrophy of the chondrocytes in growth plates. Under the assumption that the behavior of these cells depends on biochemical and mechanical factors, a presentation is made of a computational finite element model simulating the behavior of the human distal femoral growth plate. A two-dimensional domain is used to identify the regions of metaphyseal and epiphyseal trabecular bone covering the growth plate and the inert and columnar cartilage regions. Model validation was based on the histology corresponding to the distal femoral growth plate of a two-year old boy. The results obtained show that the model simulates the growth and behavior of the metaphyseal plate as regulated by its cellular activity and mechanical loads.

Key words: growth plate, finite elements, femur, hypertrophy, chondrocytes.

---

 

 

INTRODUCCIÓN

La placa de crecimiento es una estructura cartilaginosa en la que se encuentran condrocitos en estados de reserva, proliferación e hipertrofia. La histología permite identificar tres zonas que coinciden con los estados de los condrocitos y cuyos anchos varían de acuerdo a la especie.¹

En los seres humanos, la placa posee una zona ancha de cartílago inerte que separa al cartílago columnar del hueso trabecular epifisial, la cual no contribuye con el crecimiento.² Los huesos largos crecen longitudinalmente gracias a la actividad de las dos placas de crecimiento que se encuentran ubicadas en sus extremos, las cuales se encuentran reguladas por factores sistémicos y locales, tanto de tipo bioquímico como mecánico.

El factor bioquímico local más importante que regula el comportamiento de la placa de crecimiento es el bucle negativo de interacción activador-inhibidor que conforman la hormona paratiroidea relacionada (PTHrP) y el Indian Hedgehog (Ihh).³ Por otro lado, se sabe que las cargas mecánicas regulan la proliferación e hipertrofia de los condrocitos de la placa, de acuerdo con la ley de Heuter-Volkmann y los principios descritos por Delpech.⁴ Varios trabajos experimentales^5-7 han permitido cuantificar el efecto de la modulación mecánica sobre la tasa de crecimiento y las alteraciones que esta produce en la placa. Stokes y otros⁶ han demostrado que, al aplicar cargas sostenidas de tensión y compresión, el crecimiento es más sensible al cambio en la elongación de los condrocitos hipertróficos que al cambio en el número de nuevas células producidas, por lo tanto puede afirmarse que la carga mecánica tiene un efecto mayor sobre la zona hipertrófica que en la proliferativa.

El comportamiento de la placa de crecimiento durante el crecimiento endocondral ha sido modelado empleando el método de los elementos finitos. En general, los modelos empleados pueden clasificarse de acuerdo con el factor regulador involucrado: bioquímico o mecánico. Los modelos de regulación bioquímica, como los desarrollados por Brouwers y otros⁸ o Garzón-Alvarado y otros,⁹ tienen en cuenta el bucle regulador PTHrP-Ihh y su efecto sobre la diferenciación de los condrocitos proliferativos a hipertróficos. Los modelos de regulación mecánica más representativos han sido desarrollados por Stokes y otros⁷ y Carter y otros.¹⁰ El modelo de Carter y otros¹⁰ describe un tensor de crecimiento isotrópico en función de las componentes esfuerzo deviatórico e hidrostático, mientras que el modelo de Stokes y otros⁷ está basado en evidencia experimental y describe el crecimiento longitudinal en función del esfuerzo axial tensivo o compresivo. Ambos modelos fueron comparados por Lin y otros¹¹ para simular el crecimiento en una vértebra T7 bajo diversos tipos de carga. A partir de aquel artículo se puede concluir que el modelo de Carter y otros¹⁰ no involucra intrínsecamente la dirección de crecimiento y es poco capaz de predecir el retardo del crecimiento bajo cargas compresivas, mientras que el modelo de Stokes y otros⁷ puede verse limitado en su uso a aplicaciones que no involucren condiciones complejas de carga ya que no involucra el efecto de los esfuerzos no axiales.

Aunque los modelos existentes simulan adecuadamente el comportamiento de la placa de crecimiento ante cargas mecánicas, ambos describen tanto el crecimiento "de línea base" como su modulación mecánica desde un punto de vista fenomenológico, sin modelar detalladamente el efecto de las cargas sobre los condrocitos de las zonas proliferativa e hipertrófica, de tal forma que la elongación del hueso se simula mediante deformaciones térmicas equivalentes.¹¹ Adicionalmente, las implementaciones computacionales realizadas hasta ahora consideran los tejidos como materiales ortotrópicos o transversalmente isotrópicos, pero ignoran por completo la distribución y concentración celular de los condrocitos en cada una de las zonas de la placa. Por lo anterior, el objetivo principal de este trabajo es desarrollar un modelo por elementos finitos que describa desde el punto de vista biológico y simule computacionalmente el comportamiento de la placa de crecimiento del fémur distal. Para este fin, se empleó un dominio bidimensional en el que se representa la estructura de la placa de crecimiento distal del fémur humano. Se programó en FORTRAN un elemento de usuario UEL para ABAQUS, el cual modela el ciclo celular en cada una de las columnas de condrocitos. Para validar el modelo, se empleó la histología de la placa distal del fémur de un niño de dos años, logrando simular su crecimiento de línea base durante 31 días.

 

MÉTODOS

La hipótesis principal del modelo propuesto es que el crecimiento longitudinal del hueso se debe principalmente a la proliferación e hipertrofia de los condrocitos de la placa de crecimiento, los cuales se encuentran organizados por columnas. Ambos procesos celulares se ven regulados por fenómenos bioquímicos y mecánicos.¹² A continuación se describe el modelo matemático empleado y su implementación computacional.

Modelado matemático

Los elementos principales del modelo matemático empleado son los siguientes:

a) Teniendo en cuenta que el bucle regulador PTHrP-Ihh presenta un patrón de Turing inestable en el espacio pero estable en el tiempo,⁹ se supone que su mecanismo de expresión es insensible a las cargas mecánicas.¹³ Este hecho explica, en cierta medida, los resultados experimentales reportados por Villemure y otros,¹⁴ en los cuales la diferenciación de condrocitos proliferantes a hipertróficos, in vitro, es insensible ante las cargas mecánicas.

b) De acuerdo con Stokes y otros⁷ se asume que en la dirección de crecimiento no existe matriz extracelular entre los condrocitos hipertróficos y que en estado estable todos los nuevos condrocitos completan su diferenciación de proliferativos a hipertróficos. Por lo tanto, el crecimiento por día G puede expresarse como

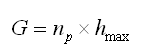
(1 )

donde es el número de condrocitos que proliferan por unidad de tiempo (células/día) y es la altura máxima, en µm, que alcanzan los condrocitos en la zona hipertrófica.

c) La descripción de la distribución y concentración celular¹³ en la placa de crecimiento se realiza a través de los tensores de segundo orden transversalmente isotrópicos definidos matemáticamente por Garzón-Alvarado y otros¹² como

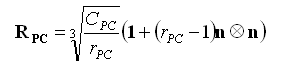
(2)

 

 

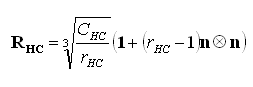
(3)

donde y son los tensores de distribución para los condrocitos proliferativos e hipertróficos, respectivamente, y son las relaciones del número de células proliferativas e hipertróficas en la dirección preferencial de crecimiento n al número de células en la dirección ortogonal, y son las concentraciones de condrocitos proliferativos e hipertróficos y 1 es el tensor unitario de segundo orden.

d) Basado en el modelo matemático propuesto por Garzón-Alvarado y otros,¹² la tasa de crecimiento puede escribirse como:

(4)

donde y son los tensores de velocidad de deformación debidos a la proliferación e hipertrofia de los condrocitos, respectivamente. El crecimiento en la zona proliferativa se debe a la mitosis celular, por lo tanto está dado por

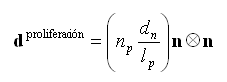
(5)

donde es el ancho del condrocito en dirección preferencial de crecimiento n y es el ancho de la zona proliferativa. Por otro lado, el crecimiento en la zona hipertrófica se debe a la elongación que sufren los condrocitos durante su diferenciación de proliferativos (forma ovoide) a hipertróficos (forma cuasi esférica):¹²

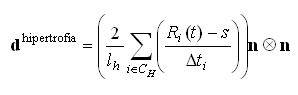
(6)

donde es el radio instantáneo del i-ésimo condrocito en la dirección del crecimiento una vez inicia la hipertrofia, es el radio menor del condrocito (en estado proliferativo, ), es el ancho de la zona hipertrófica y es el tiempo que ha transcurrido desde que el i-ésimo condrocito entra a la fase de hipertrofia y alcanza un radio . Este tiempo está limitado por el tiempo máximo de hipertrofia, el cual representa el tiempo requerido para que un condrocito proliferativo madure a uno completamente hipertrófico.

e) De acuerdo con Stokes y otros⁷ el tamaño final del condrocito hipertrófico depende del cambio en las cargas mecánicas, por lo tanto se supone una función de crecimiento del radio en función del cambio de esfuerzo en la dirección preferencial de crecimiento :

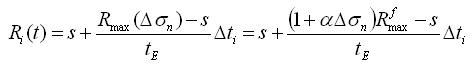
(7)

donde es la diferencia entre el esfuerzo actual en la dirección preferencial de crecimiento y el esfuerzo bajo condiciones fisiológicas , es el radio de la esfera que representa al condrocito hipertrófico alcanzado bajo condiciones de carga fisiológica y a es el cambio en el tamaño máximo del condrocito por unidad de esfuerzo. Obsérvese que .

Implementación computacional

El conjunto de ecuaciones fueron solucionadas numéricamente usando el método de los elementos finitos. Se implementó un elemento bidimensional de deformación plana con cuatro nodos mediante una subrutina de usuario UEL en FORTRAN para el software ABAQUS. Para validar el modelo computacional, se simuló el comportamiento de la placa de crecimiento del fémur 12 distal de un niño de dos años bajo condiciones fisiológicas.

Como se ilustra en la figura 1, se empleó un dominio bidimensional cuadrado de 8 mm de lado, dividido horizontalmente en seis regiones: las regiones superior e inferior corresponden al hueso trabecular epifisial y metafisial, respectivamente, mientras que las regiones interiores corresponden a las zonas de hipertrofia y proliferación del cartílago columnar y a la zona de cartílago inerte. Para simular el crecimiento producido por mitosis, se ha incluido una delgada franja de cartílago proliferativo entre las zonas de cartílago columnar e inerte.

El ancho de cada una de las zonas de cartílago se consigna en la tabla 1. El ancho de la zona hipertrófica se calculó de acuerdo al tamaño promedio del condrocito hipertrófico y al número de células hipertróficas por columna , de la forma

(8)

mientras que el ancho de la zona proliferativa se calculó restándole al ancho de la zona columnar el ancho de la zona hipertrófica :

(9)

Con base en la histología reportada por Kember y Sissons2 para la placa femoral distal de un niño de 2 años, se modelaron 104 columnas de condrocitos con 49 células en estado proliferativo y prehipertrófico, y 6 células hipertróficas () con un tamaño promedio de 30 µm. Se empleó una separación entre columnas de condrocitos en la zona proliferativa de 76,29 µm. Para realizar el enmallado por elementos finitos se definieron diferentes tamaños de elemento para cada zona del dominio, de forma tal que para los elementos de la zona proliferativa se tenía que y para los de la zona hipertrófica .

 

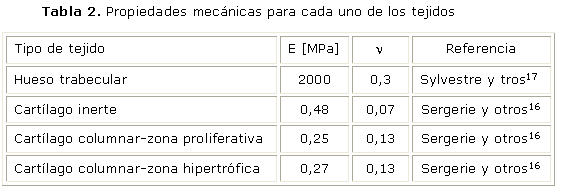
Siguiendo un enfoque similar al propuesto por Piszczatowski¹⁵ y con el fin de simplificar el modelo, todos los tejidos son tratados como materiales isotrópicos lineales y sus propiedades mecánicas se resumen en la tabla 2. Se tuvo en cuenta el cambio de propiedades mecánicas para cada una de las zonas de la placa de crecimiento, de acuerdo al estudio de Sergerie y otros¹⁶ en cerdos.

 

Para simular el crecimiento se empleó un esquema iterativo incremental en el cual el intervalo de tiempo está definido por la tasa de producción de nuevas células en la zona proliferativa. Suponiendo que la placa de crecimiento se encuentra en equilibrio, la tasa de producción celular debe ser igual al número de condrocitos que sufren apoptosis en la zona hipertrófica. De acuerdo a lo anterior, el intervalo de tiempo se define como

 

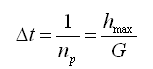
(10)

de forma tal que en cada iteración de cálculo nace un condrocito en la zona proliferativa y muere un condrocito maduro en la zona hipertrófica.

 

RESULTADOS

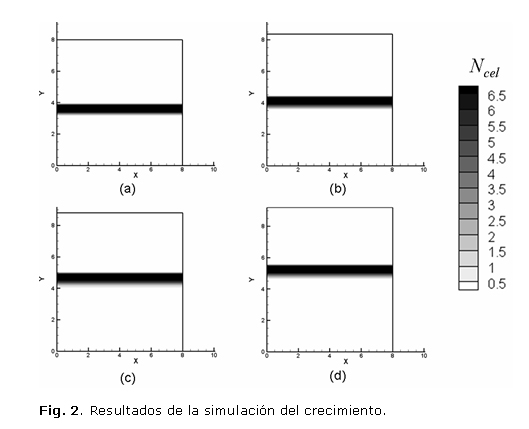
La figura 2 ilustra la evolución del dominio empleado durante un periodo de 31 días. Se observa que la placa de crecimiento mantiene su equilibrio fisiológico ya que el número de condrocitos por elemento finito en la zona columnar permanece constante. Para determinar la tasa de crecimiento del hueso se calculó el desplazamiento de la frontera entre el hueso trabecular metafisial y la placa de crecimiento durante el periodo de tiempo simulado, obteniéndose una tasa de 59,03 µm/día, lo cual corresponde a un error de 7,33 % respecto al valor de 55 µm/día reportado por Kember y Sissons.²

 

 

DISCUSIÓN

En este artículo se ha desarrollado un modelo computacional que simula el crecimiento en la placa epifisiaria desde un punto de vista biológico, a diferencia de los modelos computacionales existentes en donde la elongación del hueso se realiza mediante deformaciones térmicas equivalentes.11 El modelo permitió simular el crecimiento del fémur distal de un niño de dos años bajo condiciones fisiológicas durante 31 días; se obtuvo un error en la tasa de crecimiento de 7,32 % respecto al valor reportado por la literatura.²

Si bien el modelo computacional representa un avance en la mecanobiología computacional de la placa de crecimiento, posee ciertas limitaciones. En primer lugar, el modelo supone que el crecimiento depende únicamente de la proliferación e hipertrofia de los condrocitos, pero ignora la síntesis y degradación de la matriz extracelular como otro de los factores importantes de los que depende el crecimiento endocondral.¹ En segundo lugar, debido a que no se poseía información sobre el comportamiento mecánico de la placa de crecimiento a la que corresponde la histología, se realizó una simplificación asumiendo los tejidos como materiales isotrópicos lineales cuyas propiedades mecánicas fueron extraídas de estudios que son realizados frecuentemente en especies diferentes a la humana. Finalmente, el modelo fue implementado en un dominio bidimensional en el cual no se incluyó el anillo de Lacroix. A pesar de estas limitaciones, el modelo simula de forma completa la actividad celular de la placa de crecimiento y su regulación mecánica.

 

REFERENCIAS BIBLIOGRÁFICAS

1. Villemure I, Stokes IA. Growth plate mechanics and mechanobiology. A survey of present understanding. Journal of Biomechanics. 2009;42:1793-1803.

2. Kember, NF, Sissons, HA. Quantitative histology of the human growth plate. The journal of bone and joint surgery. 1976;58-B(4):426-35.

3. Kindblom JM, Nilsson O, Hurme T, Ohlsson C, Savendahl J. Expression and localization of Indian Hedgehog (Ihh) and parathyroid hormone related protein (PTHrP) in the human growth plate during pubertal development. Journal of Endocrinology. 2002;174:R1-R6.

4. Delpech JM. De L'Orthomorphie. 2 vol. Paris: Gabon; 1828.

5. Stokes IA, Mente PL, Iatridis JC, Farnum CE, Aronsson DD. Enlargement of growth plate chondrocytes modulated by sustained mechanical loading. Journal of Bone and Joint Surgery. 2002;84-A:1842-48.

6. Stokes IA, Clark KC, Farnum CE, Aronsson DD. Alterations in the growth plate associated with growth modulation by sustained compression or distraction. Bone. 2007;41(2):197-205.

7. Stokes A, Aronsson DD, Dimock AN, Cortright V, Beck S. Endochondral growth in growth plates of three species at two anatomical locations modulated by mechanical compression and tension. J. Orthop. Res. 2006. 24 (6): 1327-1334.

8. Brouwers JE, Van Donkelaar CC, Sengers BG, Huiskes R. Can the growth factors PTHrP, Ihh and VEGF, together regulate the development of a long bone? J Biomech. 2006;39(15):2774-82.

9. Garzón-Alvarado DA, García-Aznar JM, Doblaré M. A reaction-diffusion model for long bones growth. Biomech Model Mechanobiol. 2009. 8(5):381-95.

10. Carter, DR, Wong M. Mechanical stresses and endochondral ossification in the chondroepiphysis. J Orthop Res. 1988;6(1):148-54.

11. Lin H, Aubin C, Parent S, Villemure I. Mechanobiological bone Growth: Comparative analysis of two biomechanical modeling approaches. Medical and Biological Engineering and Computing. 2009. 47(4):357-66.

12. Garzón-Alvarado, DA, Narváez-Tovar CA, Silva, O. Um modelo matemático de la placa de crecimiento. Revista Cubana de Investigaciones Biomédicas 2011;30(1): 42-63.

13. Cancel, Grimard G, Thuillard-Crisinel D, Moldovan F, Villemure I. Effects of in vivo static compressive loading on aggrecan and type II and X collagens in the rat growth plate extracellular matrix. Bone. 2009;44(2):306-15.

14. Villemure, Chung MA, Seck CS, Kimm MH, Matyas JR, Duncan NA. Static compressive loading reduces the mRNA expression of type II and X collagen in rat growth-plate chondrocytes during postnatal growth. Connect. Tissue Res. 2005;46 (4-5):211-19.

15. Piszczatowski, S. Material aspects of growth plate modelling using Carter's and Stokes's approaches. Acta of Bioengineering and Biomechanics. 2011. 13(3): 3-14.

16. Sergerie K, Lacoursiere MO, Levesque M, Villemure I. Mechanical properties of the porcine growth plate and its three zones from unconfined compression tests. J. Biomech. 2009;42(4):510-16.

17. Sylvestre, P, Villemure, I, Aubin, C. Finite element modeling of the growth plate in a detailed spine model.Med Bio Eng Comput. 2007;45:977-88.

 

 

Recibido: 9 de septiembre de 2011.
Aprobado: 30 de septiembre de 2011.

 

 

Carlos Alberto Narváez-Tovar. Facultad de Ingeniería Mecánica. Universidad Santo Tomás. Bogotá, Colombia. Correo electrónico: [e-mail]