ARTÍCULO ORIGINAL

 

Modelado de la degradación hidrolítica de un implante óseo

 

Modeling of the hydrolytic degradation of a bone implant

 

 

Ing. Diego Alexander Garzón-Alvarado,^I MSc. Marco Antonio Velasco Peña,^II MSc. Carlos Alberto Narváez-Tovar^I

^IUniversidad Nacional de Colombia. Bogotá, Colombia.
^IIUniversidad Santo Tomás. Bogotá, Colombia.

 

 

---

RESUMEN

Una de las áreas más importantes de la ingeniería de tejidos es la investigación sobre la regeneración y sustitución del tejido óseo. Para cumplir con estos requisitos, los implantes óseos han sido desarrollados para permitir la migración de las células, el crecimiento del tejido, el transporte de los factores de crecimiento y nutrientes y la renovación de las propiedades mecánicas. Los implantes están hechos de diferentes biomateriales y se han fabricado utilizando varias técnicas que, en algunos casos, no permiten un control total sobre el tamaño y la orientación de los poros que caracterizan a la microestructura del andamio. Desde esta perspectiva, se propone el uso de un sistema de reacción difusión para lograr las características geométricas de la matriz ósea. La validación de esta hipótesis se realiza a través de simulaciones de la geometría obtenida por un sistema de reacción-difusión junto con un modelo de degradación por hidrólisis en elementos tridimensionales representativos.

Palabras clave: reacción-difusión, hueso, andamios estructurales, osificación, cicatrización.

---

ABSTRACT

Research into bone tissue regeneration and substitution is one of the most important components of tissue engineering. In compliance with these requirements, bone implants have been developed which allow cell migration, tissue growth, the transport of growth factors and nutrients, and the renewal of mechanical properties. Implants are made of various biomaterials, and they have been manufactured using techniques which not always allow total control of the size and orientation of the pores involved in the microstructure of the scaffold. From this standpoint, a reaction-diffusion system is proposed for the achievement of appropriate geometric features in the bone matrix. The hypothesis is validated through simulations of the geometry obtained with a reaction-diffusion system and a model of hydrolytic degradation in three-dimensional representative elements.

Key words: reaction-diffusion, bone, structural scaffolds, ossification, healing.

---

 

 

INTRODUCCIÓN

El hueso es un tejido conectivo mineralizado compuesto principalmente por cristales de hidroxiapatita en una matriz de colágeno y forma el esqueleto de los vertebrados. Hay dos tipos de tejidos óseos: el cortical y el trabecular. Aunque son biológicamente similares, difieren en su estructura. El hueso cortical es compacto y está ubicado en la superficie mientras el trabecular es un patrón esponjoso hueco formado por trabéculas y placas. Los huesos cumplen funciones mecánicas, sintéticas y metabólicas. La búsqueda de elementos que ayuden a suplir dichas funciones requiere la investigación interdisciplinaria de la ingeniería, la biología y la medicina para cumplir requisitos que van desde las propiedades mecánicas hasta la biocompatibilidad.¹

Materiales sintéticos como cerámicos, polímeros o materiales compuestos están en constante desarrollo para ser usados como implantes óseos. Los materiales cerámicos están basados en fosfatos de calcio como la hidroxiapatita y los biovidrios. Se distinguen por tener buenas propiedades osteoinductivas pero bajas propiedades mecánicas y dificultades en su proceso de fabricación.² A su vez, polímeros tales como los derivados del ácido poliglicólico (PGA) y del ácido poliláctico (PLA), tienen buenas propiedades mecánicas y de biodegradabilidad, que pueden variar de acuerdo con su peso molecular; también se caracterizan por su fácil conformabilidad, pero tienen baja capacidad osteoinductiva con respecto a los cerámicos.³

Los materiales compuestos cerámica-polímero combinan las propiedades de los materiales de base: buena resistencia mecánica, osteoconductividad y fácil conformabilidad.⁴ Las cerámicas basadas en fosfatos de calcio muestran alta osteoconductividad, pero bajas tasas de degradación.⁵ La degradación en cerámicas como los fosfatos de calcio se debe a mecanismos como la disolución, la precipitación, la hidrólisis y la transformación de fase.⁶ Por otra parte, la degradación de los polímeros se produce por el mecanismo de hidrólisis y la acción de enzimas.⁷ Biopolímeros como los poliésteres (el PGA y el PLA), la policaprolactona o los poliuretanos se degradan por hidrólisis, mientras que los poliaminoácidos y el colágeno se degradan por la acción enzimática. Teniendo en cuenta que el PLA es de fácil obtención y procesamiento, además de amplio uso médico,⁸ la erosión de este polímero, considerando un proceso de difusión del agua en su interior y posterior hidrólisis, ha sido estudiada por varios autores.^9-13

Aunque los implantes óseos, generalmente, son objetos sólidos hechos a medida e implantados en el sitio del defecto, otro enfoque en el uso de biomateriales para el tejido óseo son los cementos óseos. Por lo general, estos son empleados para fijar reemplazos articulares y para llenar las cavidades en los huesos en procedimientos como la vertebroplastia y la cifoplastia. Su principal ventaja es el mínimo de preparación e intervención invasiva. Del mismo modo, al igual que los procesos convencionales, la porosidad puede ser alcanzada mediante el uso de partículas biodegradables que actúan como porogeneradores.^14,15

Sin embargo, ni los implantes ni los cementos óseos son los mecanismos que la naturaleza aplica en el proceso de morfogénesis. Desde Turing,¹⁶ muchos autores han postulado el uso de los sistemas de reacción-difusión (RD) para modelar los patrones y estructuras que se encuentran en los organismos vivos.¹⁷

Los sistemas de RD son modelos matemáticos inspirados en las reacciones químicas, que describen la concentración y distribución espacial de una o más sustancias reactivas que actúan como morfogeneradores. Siguiendo esta línea, como una posible alternativa a los procesos existentes de fabricación de andamios, se plantea la hipótesis de que un sistema de reacción-difusión puede ser empleado para generar implantes controlando el porcentaje de porosidad, el tamaño de los poros y su interconexión. De esta forma se pueden ajustar las propiedades geométricas y físicas apropiadas para una aplicación clínica en particular.

Este artículo tiene como objetivo explorar la degradación a partir del proceso de hidrólisis en estructuras que pudiesen ser obtenidas mediante un sistema de RD hipotético. Para ello, mediante variaciones en los valores del sistema RD se obtienen diferentes volúmenes representativos que provocan cambios en la periodicidad de los patrones obtenidos en la arquitectura interna del andamio y, después de eso, se aplica un modelo de degradación debido a hidrólisis, propuesto por Adachi y otros,⁹ a cada uno de los volúmenes representativos.

 

MÉTODOS

Para la generación de los elementos representativos de volumen se trabajará el modelo propuesto por Garzón y otros,¹⁸ del cual se muestra un resumen a continuación. En un principio, se supone un modelo de sistema de RD de Schnakenberg como el mencionado por Murray,¹⁷ en el que la velocidad de reacción es directamente proporcional al producto de las concentraciones activas de los reactivos, por lo que la cinética de reacción viene dada por:

(1)

Donde A, B, K, K₁, K₂, K₃ y K₄ son constantes positivas. Por lo tanto, el sistema anterior solo depende de las variables X e Y.

Por otro lado, se supone que se obtiene un biomaterial obtenido mediante la polimerización de uno de los reactivos en el sistema de RD, como resultado de su nivel de concentración. Una vez que el sistema de RD llega a la estabilidad, el biomaterial hereda el patrón espacial. Para modelar este proceso, se asume que la polimerización sigue una ley similar a la propuesta por Ludwig y otros, como se ha mencionado por Murray.¹⁷ Este proceso se describe a continuación:

 

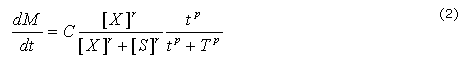
Donde S es el valor del umbral de la concentración de reactivo X que inicia la polimerización, M es la concentración de biomaterial, t es el tiempo desde el inicio del proceso de polimerización, T es el valor umbral de tiempo en el que se inicia la polimerización, C es una velocidad constante y P y R son constantes que definen la pendiente de la función de umbral.

A partir del modelo del sistema de RD se hace un análisis del número de onda para dicho sistema pues es el que permite regular la distribución de los poros. Desde el análisis de estabilidad lineal referido por Murray¹⁷ se propone el proceso de diseño de un andamio mediante la manipulación de los parámetros de la reacción química, la difusión y la función de la polimerización. Los parámetros adimensionales de la RD del sistema d, g A y B permiten el control de la estructura y la formación de patrones de Turing. Por el contrario, en el diseño de un andamio, se requiere conocer el número de onda necesario para definir el número de poros en una dirección, además de A y B, después de esto, se obtienen los valores de d y g. El número de onda indica el número de medias ondas sinusoidales en cada una de las direcciones x e y.

El análisis de la gama es posible encontrar los valores de m y n los definen la distribución de los poros en el dominio. Por ejemplo, en un dominio rectangular, el número de poros total en la dirección x está dada por m/2Lx y n/2Ly en la dirección y. Para ver como obtener los valores de m y n se puede consultar la referencia de Garzón y otros.¹⁸

Para el modelo de degradación se supone que el biomaterial es un polímero que se degrada por hidrólisis de manera similar a como lo hace el PLA. En este estudio se adopta el modelo propuesto por la degradación de Adachi y otros.⁹ A continuación se hace un resumen de dicho modelo. Se inicia considerando que el módulo de elasticidad Es es proporcional al peso molecular del polímero:

 

 

 En (3) E_s0 es el módulo de elasticidad a un peso molecular inicial W0.

Mientras tanto, el peso molecular cambia en el tiempo debido a un proceso de hidrólisis:

 

 

Donde b es una constante del biomaterial y c es el valor de la concentración de agua que se encuentra entre 0 y 1, y es función de la ecuación de difusión:

 

Donde a es el coeficiente de difusión de agua en el biomaterial.

 

RESULTADOS

Esta sección presenta las situaciones modeladas para estudiar tanto la formación del patrón interno del implante como su posterior degradación. Las pruebas iniciales se realizaron para verificar la predicción hecha por la teoría, así como los números de onda que se predicen por la teoría de estabilidad lineal. Las pruebas se han desarrollado en un volumen cúbico, con el fin de obtener diferentes estructuras representativas. Las pruebas numéricas se llevaron a cabo en un cubo con un tamaño de 2,4 mm de longitud de onda con tres números diferentes: (2,2,0), (2,2,2) y (4,2,2). Los parámetros de RD fueron elegidos con el fin de obtener estructuras porosas con las periodicidades definidas por los números de onda anteriormente propuestos. La malla de elementos finitos consta de 17 576 nodos y 15 625 elementos. Además, todas las simulaciones emplean un incremento de paso de Dt = 0,01, hasta alcanzar los 1 000 pasos. Por otro lado, cada una de las estructuras se logra al heredar el patrón de Turing. La elección de las condiciones iniciales aleatorias pueden considerarse similares al caso de la inyección de dos sustancias en una cavidad en donde no se puede determinar con precisión la concentración de cada uno al comienzo de la reacción. Además, se consideró el flujo nulo en todas las fronteras del dominio. Finalmente, se aplica el modelo de la degradación para examinar su evolución microestructural debido a la hidrólisis.

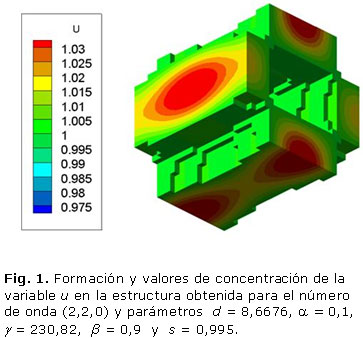
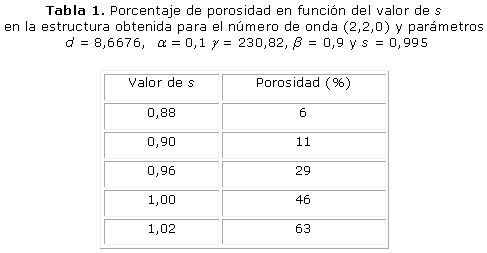
La figura 1 muestra la formación de la microestructura obtenida para la variable u, cuando s es igual a 0,995 y con el número de onda (2,2,0). Los parámetros del sistema RD fueron d = 8,6676, a= 0,1, b = 0,9 g = 230,82. El patrón de Turing se estabilizó en un tiempo adimensional t = 5,8, con una porosidad resultante del 46 %. El ancho trabecular obtenido de la celda unidad es de 1,2 mm. El cambio de la porosidad está en función del valor umbral de la polimerización s como se observa en la tabla 1.

 

 

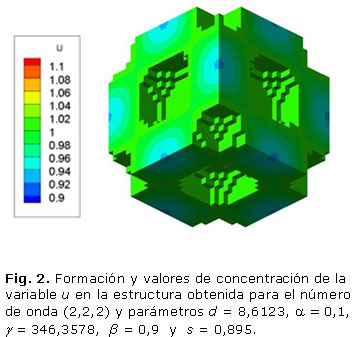
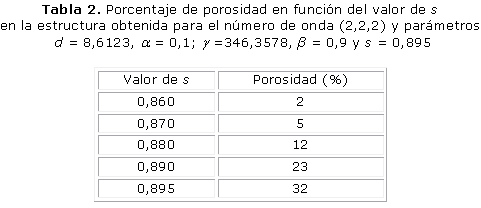
La figura 2 muestra las células de la unidad de andamio para obtener el número de onda (2,2,2). Los parámetros utilizados en el sistema de RD fueron d = 8,6123, a = 0,1, b = 0,9 y g = 346,3578, cuando s es igual a 0,895. Esta unidad presenta una porosidad de 32 %, una anchura trabecular de 1,2 mm y un tiempo de estabilización adimensional t = 8,4. Una vez más, la porosidad depende del valor umbral de polimerización s, como se ve en la tabla 2.

 

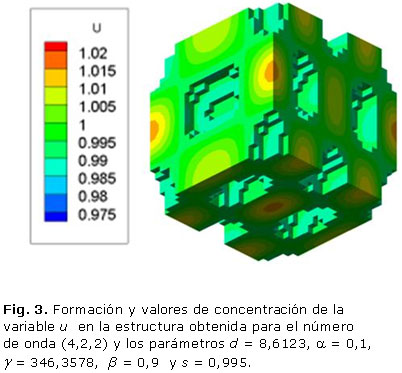
La figura 3 muestra algunos ejemplos de la estructura obtenida con el número de onda (4,2,2) cuando s = 0,995. Los parámetros del sistema RD son d = 8,5736, a = 0,1, g = 700,4675, b = 0,9. El patrón de Turing se estabilizó en un tiempo adimensional t =28,8, con una porosidad resultante del 29,6 %. Esta celda unitaria tiene una anchura de trabéculas de 0,6 mm. En cuanto a los dos números de onda presentados anteriormente, el cambio en la unidad de la porosidad es una función del valor umbral de polimerización s, como se ve en la tabla 3.

 

Los resultados presentados en las figuras 1, 2 y 3 demuestran que a mayores números de onda aumenta el tiempo de estabilización del patrón de Turing. Por otro lado, las tablas 1, 2 y 3 demuestran que la porosidad depende del valor umbral s de polimerización.

Sobre las tres geometrías obtenidas variando el número de onda, se realizaron pruebas numéricas del modelo de degradación con el fin de examinar su evolución microestructural debido a la hidrólisis. Las propiedades del material considerado para el andamio hipotético fueron un módulo de elasticidad E_s0 = 20 GPa, una relación de Poisson v_s= 0.3, un peso molecular inicial de W₀ = 70 000 g/mol, un coeficiente de difusión a = 4.0 X10-4 mm²/día y tasa de degradación constante de b = 4 000/día. Estas propiedades son similares a las del ácido poliláctico, un polímero de ancho utilizados en aplicaciones biomédicas^8,9 y los valores son tomados de Garzón-Alvarado.¹⁸ La figura 4 (a) y (b) muestra la evolución de la concentración de agua y el módulo de elasticidad, respectivamente, para la celda unidad obtenidos con el número de onda (2,2,0). Se observa que se requieren 127 días para la degradación completa.

La figura 5 (a) y (b) muestra el proceso de degradación de la unidad obtenida con el número de onda (2,2,2). La degradación completa de las células de unidad toma 118 días.

El proceso de degradación de la celda unidad (4,2,2) se ilustra en la figura 6 (a) y (b). La degradación completa de la estructura se produce después de 91 días.

La figura 7 muestra la evolución de la masa normalizada restante sobre el tiempo de degradación. Después de 20 días, la degradación se inicia y se puede observar que el uso de una serie de ondas de alta disminuye el tiempo necesario para lograr la degradación total.

 

DISCUSIÓN

El objetivo de este trabajo es mostrar el potencial de los sistemas de RD en la ingeniería de tejidos óseos. Tres patrones tridimensionales se obtuvieron mediante la variación de los parámetros del modelo de reacción-difusión de Schnakenberg para lograr microestructuras internas que podrían ser útiles para la regeneración ósea. Se aprecia que propiedades como el tamaño de los poros y la porosidad pueden ser controladas variando el valor de los parámetros a, b, d, g, Ta, s, del modelo considerado. El número de onda K obtenido determina la frecuencia de la distribución espacial de los poros, como se puede ver en las figuras 1, 2 y 3. La disminución y el aumento de los valores d y g llevó a la formación de los patrones que tienen mayor número de onda. El número de onda (2, 2, 0) se obtiene con d = 8,6676 y g = 230,82 en comparación con el número de onda (4, 2, 2) obtenido con d = 8,6123 y g = 346,36. El comportamiento no lineal de los sistemas de RD se observa cuando las pequeñas variaciones en el valor d ocasiona cambios significativos en la periodicidad del modelo obtenido. Por su parte, el parámetro s principalmente determina porcentaje de porosidad de la estructura. A mayor valor de s mayor porosidad. A pesar de que los sistemas RD son procesos dependientes del tiempo, todas las simulaciones alcanzan la estabilidad temporal después de cierto tiempo Ta, independientemente de las condiciones iniciales.

Por otro lado, como se puede observar en la figura 7, las simulaciones no muestran degradación aparente en los primeros 20 días. A partir del día 20 al día 50, aproximadamente, se observan tasas de degradación similares en las tres celdas. Finalmente, a partir del día 50 hay degradación a diferentes tasas que conducen a una mayor disminución de la masa en la celda con número de onda (4,2,2).

La implementación del modelo tiene un bajo coste computacional en comparación con otros como Leppanen,²² donde 500 000-2 000 000 pasos de tiempo se requieren en las simulaciones 3D para obtener los patrones estabilizados. Aquí, las estructuras de estabilización se obtuvieron usando 1 000 pasos de tiempo o menos.

Este trabajo ha hecho algunas consideraciones y simplificaciones que se deben tener en cuenta. El primer aspecto es la falta de datos experimentales para apoyar el modelo. Hasta donde los autores conocen, no hay sistemas de RD que originen biomateriales. Sin embargo, cabe señalar que entre el trabajo de Turing sobre los sistemas de RD como un mecanismo para la morfogénesis¹⁶ y la primera evidencia experimental²⁰ pasaron casi 30 años. La segunda consideración es que el modelo asume que, al menos, una especie permite la polimerización de un biomaterial. El tercer aspecto es la simplificación del tamaño del dominio y la forma del sistema de RD.

Varios autores como Shoji²¹ han informado de la influencia del tamaño y la forma del dominio en la forma y la estabilidad del patrón generado. Es necesario mencionar que a medida que avanza el proceso de recuperación, en el sitio de la lesión pueden producirse cambios en la geometría de dominio que podrían afectar el comportamiento del sistema de RD. Una cuarta simplificación es considerar condiciones de Neumann en los límites de dominio. En realidad, puede haber flujo en las fronteras que cambian el comportamiento del sistema de RD. También es una simplificación excesiva considerar los coeficientes de difusión y las constantes de reacción cuando estos están sujetos a diversos factores del microambiente donde se produce la reacción. Además, pueden ser estudiados otros sistemas de RD como Brusselator, Gray Scott y el Lengyel-Epstein.²² Es necesario analizar el efecto del tamaño del dominio y de los elementos con respecto a la longitud de onda de los patrones obtenidos y debería haber evaluaciones sobre el efecto del método numérico utilizado en la estabilidad y la forma del patrón generado.

A pesar de las simplificaciones y la necesidad de más estudios, este trabajo es útil por varias razones. Desde el punto de vista de la simulación numérica, ayuda en el análisis de los patrones de Turing en tres dimensiones, un área donde no se hacen muchas obras como se ha mencionado por Shoji.²¹ Desde un punto de vista funcional, este trabajo en comparación con otros^21-22 proporciona una metodología para el control de la geometría de los patrones obtenidos, que es importante para la aplicación clínica o de otro tipo de andamios desarrollados. Por último, señalamos que este trabajo proporciona una posible línea de investigación experimental que puede acercarse a la solución de problemas complejos en ingeniería de tejidos.

 

REFERENCIAS BIBLIOGRÁFICAS

1. Lanza R, Langer R, Vacanti J. Principles of Tissue Engineering. USA: Elsevier; 2007.

2. Blom A. Which scaffold for which application? Current Orthopaedics. 2007;21:280-7.

3. Hutmacher DW. Scaffolds in tissue engineering bone and cartilage. Biomaterials. 2000;21:2529-43.

4. Rezwan K, Chen QZ, Blaker JJ, Boccaccini AR. Biodegradable and bioactive porous polymer/inorganic composite scaffolds for bone tissue engineering. Biomaterials. 2006;27:3413-31.

5. Dorozhkin SV. Amorphous calcium (ortho) phosphates. Acta Biomaterialia. 2010;6:4457-75.

6. Chow LC. Solubility of calcium phosphates. Monographs in oral science. 2001;18:94-111.

7. Nair LS, Laurencin CT. Biodegradable polymers as biomaterials. Progress in Polymer Science. 2007;32:762-98.

8. Madhavan K, Nair NR, John RP. An overview of the recent developments in polylactide (PLA) research. Bioresource technology. 2010;101:8493-501.

9. Adachi T, Osako Y, Tanaka M, Hojo M, Hollister SJ. Framework for optimal design of porous scaffold microstructure by computational simulation of bone regeneration. Biomaterials. 2006;27:3964-72.

10. Göpferich A. Mechanisms of polymer degradation and erosion. Biomaterials. 1996;17:103-14.

11. Wang Y, Pan J, Han X, Sinka C, Ding L. A phenomenological model for the degradation of biodegradable polymers. Biomaterials. 2008;2:3393-401.

12. Chen Y, Zhou S, Li Q. Mathematical modeling of degradation for bulk-erosive polymers: Applications in tissue engineering scaffolds and drug delivery systems. Acta Biomaterialia. 2011;7:1140-49.

13. Kang Y, Xu X, Yin G, Chen A, Liao L, Yao Y, Huang Z and Liao X. A comparative study of the in vitro degradation of poly(l-lactic acid)/ beta-tricalcium phosphate scaffold in static and dynamic simulated body fluid. European Polymer Journal. 2007;43:1768-78.

14. Feng B, Guolin M, Yuan Y, Changshen L, Zhen W, Jian L. Role of macropore size in the mechanical properties and in vitro degradation of porous calcium phosphate cements. Materials Letters. 2010; 64:2028-31.

15. Kenny S, Buggy M. Bone cements and fillers: A review. Journal of Materials Science. 2003;14:923-38.

16. Turing A. The chemical basis of morphogenesis. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences. 1952;237:37.

17. Murray JD. Mathematical Biology II: Spatial models and biomedical applications. New York: Springer-Verlag; 1993.

18 Garzón-Alvarado D, Velasco M. Aplicación de sistemas reacción-difusión en el diseño de la geometría interna de matrices para regeneración ósea. Rev Cubana Invest Bioméd. 2011;30(1):83-96.

19. Madzvamuse A. A Numerical approach to the study of spatial pattern formation. PhD Thesis. Oxford University. 2000.

20. Nagorcka BN. Evidence for a reaction-diffusion system as a mechanism controlling mammalian hair growth. Biosystems. 1983;16:323-32.

21. Shoji H, Yamada K, Ueyama D, Ohta T. Turing patterns in three dimensions. Physical Review E. 2007;1:1-13.

22. Leppanen T, Karttunen M, Kaski K, Barrio RA. Dimensionality effects in Turing pattern formation. Int J Mod Phys B. 2003;17:5541-53.

 

 

Recibido: 10 de septiembre de 2011.
Aprobado: 25 de septiembre de 2011.

 

 

Diego Alexander Garzón-Alvarado. Universidad Nacional de Colombia, Bogotá, Colombia. Correo electrónico: [e-mail]